新建市政隧道下穿多线运营铁路地表沉降研究——以郑州火车站片区操场街隧道工程为例

郭 明 谢 璨 宋曙光 韩少辉

(1. 中铁工程设计咨询集团有限公司郑州设计院, 郑州 450006; 2. 山东建筑大学交通工程学院, 济南 250101)

引言

截至2022 年底,我国铁路营业里程达15.5 万km,我国已是铁路交通大国。 另一方面,随着城市规模的扩大,综合交通枢纽的建设和改造项目日渐增多,新建城市轨道交通工程与既有铁路线路交叉难以避免。

市政工程隧道往往埋深较浅,施工时易引起上方土体沉降,而运营铁路对于位移控制比较严格,增加了下穿运营铁路新建隧道工程的施工难度,如何降低新建隧道对运营铁路的影响,保障下穿运营铁路隧道施工安全,成为亟需解决的工程难题[1-3]。 已有许多学者开展相关研究,姚晓明等认为选择合理的施工种方法能有效地控制施工对既有铁路的影响[4-5];张恒臻等研究控制新建隧道下穿施工地表沉降的辅助施工措施[6-8];郭现钊通过理论分析、数值模拟计算、工程类比等方法,分析盾构区间隧道下穿施工引起的铁路桥梁及承台沉降、差异沉降、时程曲线,并给出安全施工防护措施[9];宋宪贺通过数值模拟与现场监测,研究盾构隧道下穿多条铁路线时铁路工程变形规律[10-11];邹浩等基于杭州地铁2 号线项目,分析盾构下穿既有铁路施工期间的各项监测数据,探究下穿既有铁路的盾构隧道施工过程中,列车轨道路基坡脚及路肩的位移变化规律[12];景路等基于弹性力学Mindlin 解,分析矩形顶管施工过程中引起地表隆起变形的因素并将其分类,得到不同因素对地表隆起变形的影响程度[13-15];焦义等基于Mindlin 解得到在顶管施工阶段地表竖向位移计算公式,揭示特殊地层下圆形顶管施工引起地层变形规律[16];由广明采用有限元数值模拟的方法,研究不同顶管的摩阻力、机头压力、土体抗力等条件下曲线顶管施工过程的地面沉降,并进行施工参数优化[17-18];孟繁增基于现场实测数据,揭示北京卵石土地区双洞单线隧道下穿施工期对既有铁路的沉降影响[19];MEI 等针对卵石地层,通过现场试验和数值模拟分析注浆悬挂综合技术对运营铁路盾构隧道的轨道沉降控制的效果[20]。

以上研究多基于隧道下穿单线铁路,对于隧道近距离下穿四线铁路的工程实例比较少。 同时,各城市工程地质条件差别较大,针对郑州地区隧道近距离穿越多线铁路工程的研究有待深入。 因此,针对郑州火车站片区操场街下穿多线铁路隧道工程,通过有限元数值模拟,研究不同开挖方法下隧道开挖引起的下穿多线运营铁路路基沉降变化规律,以期提出新建隧道下穿既有运营铁路安全施工方案,并为相似工程提供借鉴。

1 工程概述

1.1 工程简介

操场街下穿隧道工程是郑州火车站地下空间综合开发利用工程的重要组成部分,是连接火车站东西广场的重要通道。 操场街自京广路起连续下穿太和路、新甫西街、郑州火车站(火车头停车场、郑铁动车运用楼、机务段设备车间等)、一马路,向东至敦睦路,向北至大同路,全长1 377 m,操场街下穿隧道总体平面见图1。 操场街隧道包含机动车道、人通道及非机动车通道。 机动车道为双向四车道,两侧设置6 m 宽人通道及非机动车通道,分为四幅。 下穿铁路段位于直线上,在铁路西侧设置半径600 m 的圆曲线,曲线长86.772 m,然后以直线与京广路相交;东侧下穿铁路后,考虑人行道及分机动车道爬坡要求,左右两侧分别设置2 条通道展坡后与地面相接,机动车道在一马路设置北向西匝道单向进入操场街隧道,匝道半径为40 m,右幅西向东沿单向操场街接入敦睦路。 操场街隧道穿越马寨线处共4 条线路均为货运线,穿越处铁路为高路基,路基较地面高4 m 左右。

图1 操场街下穿隧道总平面

1.2 工程地质条件

场地表层为人工杂填土、素填土,其下为第四纪晚新近冲积形成粉土、粉砂以及粉质黏土。 地下水位在自然地面以下9.8~11.8 m(高程约91.0 m),属第四系松散岩类孔隙潜水。 地下水主要补给来源为大气降水入渗补给和地下水径流补给,主要排泄方式为人工开采和地下水径流。 场地地下水位年变幅1.0 ~2.0 m,本场区3~5 年内最高水位7.0 m(高程约94.0 m),历史最高地下水位埋深在地面下5.0 m(高程约96.0 m)。

2 开挖方法初选

施工方法对结构形式和隧道土建工程造价有决定性影响。 施工方法一方面受工程地质和水文地质条件、环境条件(地面建筑物和地下构筑物的现状、道路宽度、交通状况)等多种因素的制约,同时也会对工程的难易程度、工期、造价、使用功能等产生直接影响。根据本工程的地质、环境情况,待选开挖方法有明挖法、盖挖逆作法、圆形盾构法、类矩形盾构法、矩形顶管法、管幕暗挖法。

郑州火车站为中心枢纽站,列车运行繁忙,确保铁路运营安全为本次设计的重中之重。 根据现有控制因素,股道众多,道岔过密,无法采用架空股道的常规方式,故传统的明挖法、盖挖逆筑法等传统的施工方法不适合本工程。 同时,受两侧衔接道路平面位置限制,纵断下调空间受限制,若采用圆形盾构法,其断面利用率低,覆土深,与一马路衔接困难,难以满足交通功能的要求。 类矩形盾构虽然克服了圆形盾构法断面利用率低的困难,但施工经验较少,且本工程机动车道断面净尺寸要求≮9 m,顶部荷载较大,管片拼装从目前的技术不能满足结构受力的要求。 因此,主要研究了矩形顶管法与管幕法2 种开挖方法。

3 矩形顶管法对铁路轨道的影响分析

3.1 计算模型及参数

矩形顶管段隧道埋深6.1 m,总宽度为36.9 m,其中机动车道、人通道及非机动车通道顶管管壁厚度均为0.55 m,人通道及非机动车通道结构净高4.75 m,净宽6.1 m,转角设置0.95 m 圆角,机动车道结构净高6.5 m,净宽9 m,转角设置1.55 m 圆角,其标准横断面见图2。 每节管片纵向长度为1.5 m,管片横向安全距离为0.9 m。 同时,由于本工程顶管距离达到320 m,管壁周围土体长时间被膨润土泥浆浸泡、受顶管顶进扰动,会发生不均匀变形。 为保证铁路路基的整体稳定性,减小局部变形,在顶管周围设置管幕结构(后续的管幕暗挖法中为隧道结构外侧均打设管幕结构),共设置47 根ϕ900 mm(壁厚20 mm)钢管,钢材为Q345 钢,钢管通过咬合,形成半封闭结构。 管幕与顶管之间留20 cm 空隙,避免管幕变形触碰顶管。 计算模型尺寸为35.4 m×20 m×60 m,模型上表面为自由面,其他各面均约束法向位移。 土体采用M-C 模型。操场街隧道下穿铁路段数值计算模型见图3。

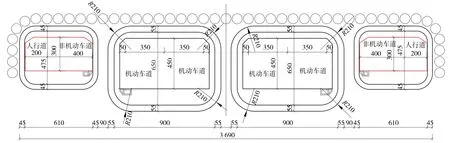
图2 矩形顶管法隧道横断面(单位:cm)

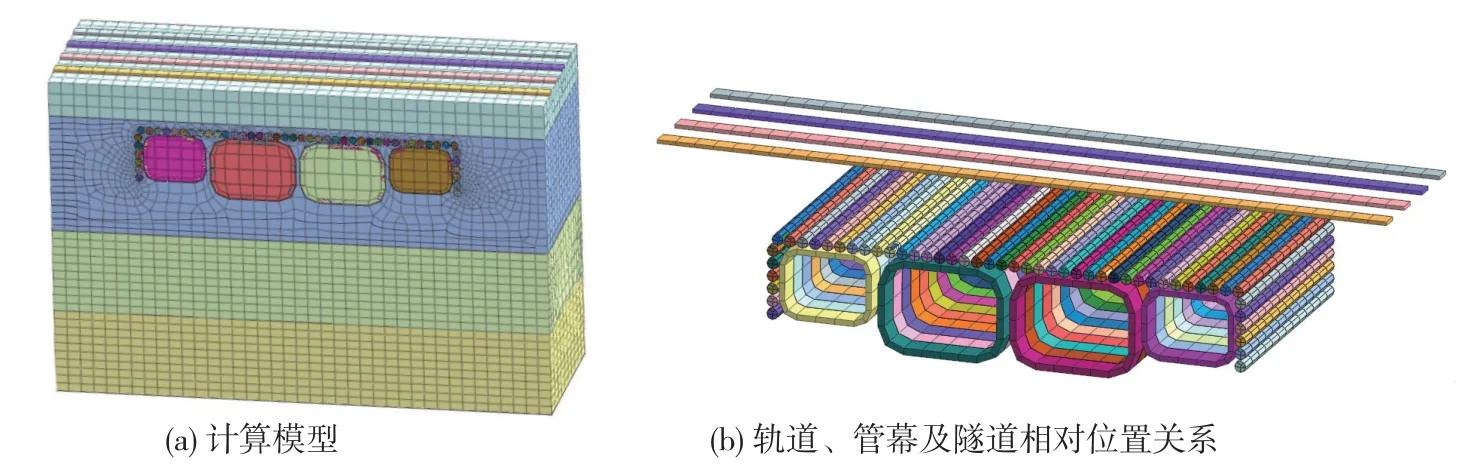
图3 矩形顶管法隧道开挖数值计算模型

地层采用实体单元模拟,根据地勘资料,对地层进行合并简化,地层参数和结构力学参数见表 1、表 2。根据TB 1002—2017《铁路桥涵设计规范》,计算模型须施加ZKH 活载,均布荷载qk=85 kN/m,集中荷载pk=250 kN/m,集中荷载施加在路面中心处。

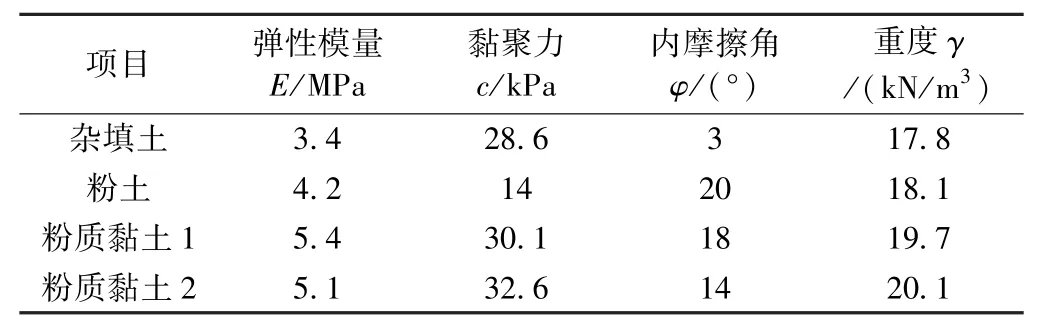
表1 地层物理力学参数

表2 结构物理力学参数

3.2 计算工况

采用矩形顶管法开挖时,先进行管幕超前支护,模拟进尺为2 m。 矩形顶管法顶进工序示意见图4。 顶进顺序为:ϕ900 mm(壁厚20 mm)管幕、①号矩形管片、②号矩形管片、③号矩形管片、④号矩形管片。 数值计算工序见表3。

表3 数值计算工序

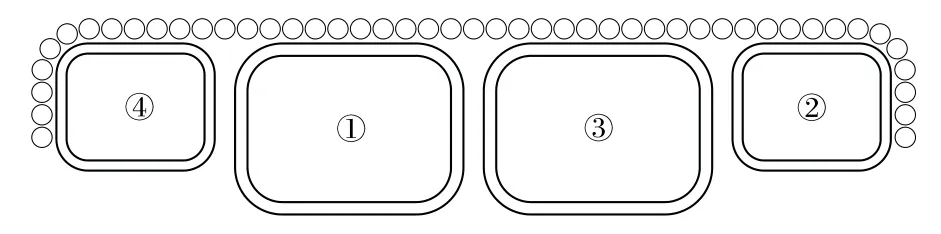
图4 矩形顶管法顶进工序示意

3.3 计算结果分析

为了消除边界效应的影响,取铁路中线与隧道中线交界处的断面作为研究对象,布置测点监测轨道沉降及管片应力。 顺铁路方向共布置21 个测点,距离中心点(Z)距离分别为2,4,6,9,12,15,18,22,26,30 m,用于监测轨道沉降;在横断面上共对称布置8 个测点,分别在管片拱顶、拱肩、拱腰、拱脚和仰拱。

(1)轨道沉降分析

铁路运营及不同施工步下轨道沉降云图见图5,不同施工步下及隧道顶进完成后轨道沉降曲线见图6。

图5 铁路运营及不同施工步引起的轨道沉降云图

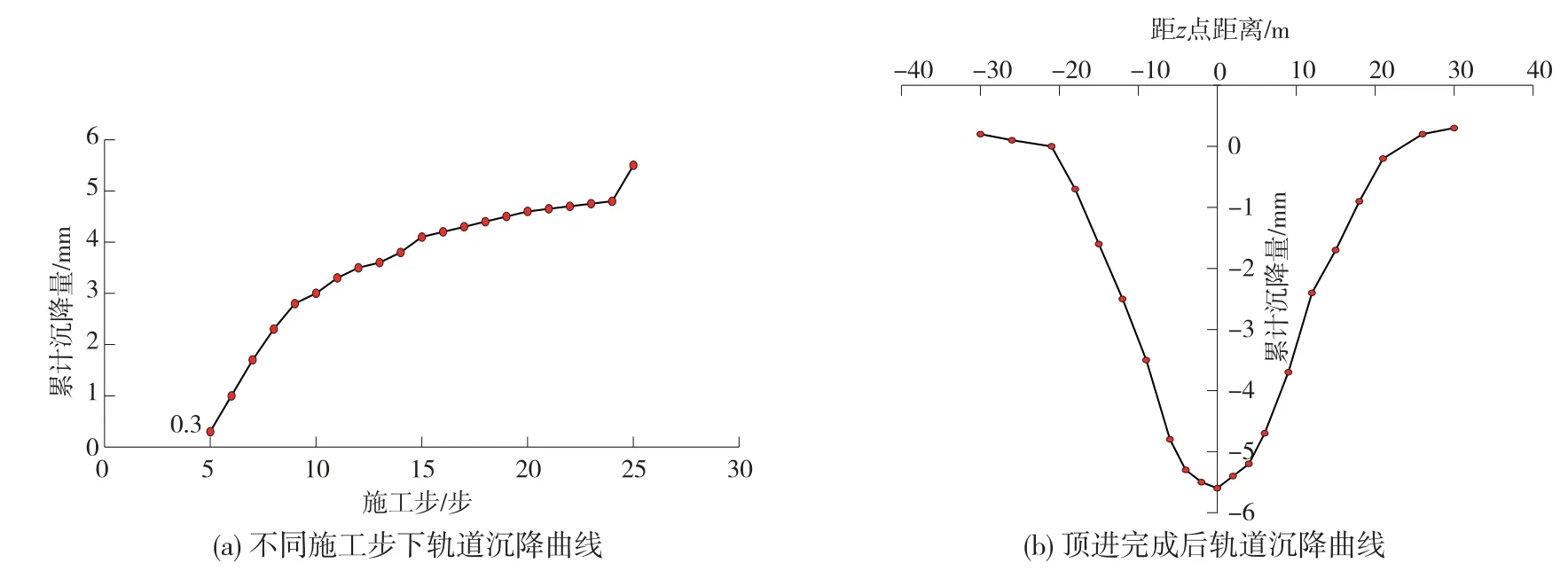
图6 不同施工步下及隧道顶进完成后轨道沉降曲线

由图5 可知,地表路基中心点处沉降位移最大为5.6 mm,从中心点竖直方向垂直于隧道方向两侧各监测点沉降量逐渐减小,至中心点两侧20 m 处沉降值为0.1 mm,顶进引起的沉降已经很小;中心点两侧30 m处轨道位移由沉降变为隆起,隆起值为0.3 mm,隆起主要由边界效应引起,可忽略其变形。 由图6 可知,随着隧道的顶进,轨道沉降越来越大,顶进完成时轨道沉降为5.6 mm,施工时应采取相应控制措施避免轨道沉降过大对铁路运营的影响。

(2)矩形顶管应力分析

顶进过程中管片第一、三主应力云图见图7,取顶进过程中管片各监测点的第一、三主应力数据绘制变化曲线,见图8。 由图7、图8 可知,管片第一主应力表现为拉应力,最大值为1.35 MPa;管片第三主应力表现为压应力,最大值为10.09 MPa。

图7 顶进过程中管片的第一、三主应力云图

图8 管片各监测点的第一、三主应力变化曲线

4 管幕暗挖法对铁路轨道的影响分析

4.1 计算模型

管幕暗挖法隧道结构采用机动车道框架、人通道及非机动车通道分离的结构形式。 人通道及非机动车通道结构净高4.9 m,结构净宽6.1 m,边墙厚0.6 m,顶底板厚0.7 m;机动车道结构净高6.5 m,单孔净宽9 m,边墙厚0.8 m,中墙厚0.7 m,底板厚0.9 m。 隧道结构外侧采用ϕ900 mm 管幕全周布置(112 根),机动车道和非机动车道共用管幕,管幕钢管间距为100 mm,其标准横断面见图9。

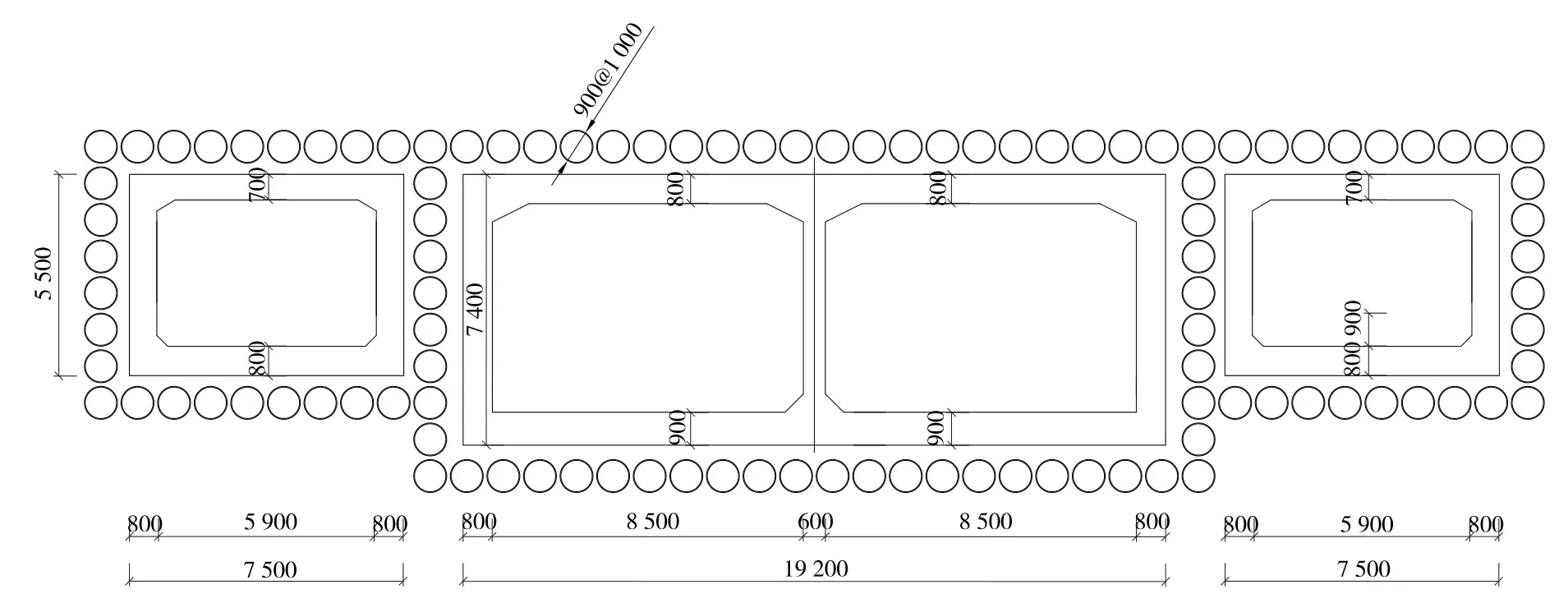
图9 管幕暗挖法隧道标准横断面(单位:mm)

计算模型尺寸为35.4 m×20 m×60 m,数值模型上表面为自由面,其他各面均约束法向位移,管幕暗挖法隧道计算模型见图10。 其他参数同3.1 节。 管幕暗挖法数值计算工序见表4。

表4 管幕暗挖法数值计算工序

图10 管幕暗挖法隧道计算模型

4.2 计算结果分析

取铁路中线与隧道中线交界处的断面作为研究对象,布置测点监测轨道沉降及管片应力。 在研究断面的地表,顺铁路方向共布置21 个测点,距离中心点(Z)距离分别为2,4,6,8,10,16,18,22,26,30 m。

(1)轨道沉降分析

铁路运营及不同施工步下轨道沉降云图见图11,不同施工步下及隧道顶进完成后轨道沉降曲线见图12。

图11 铁路运营及不同施工步引起的轨道沉降云图(单位:mm)

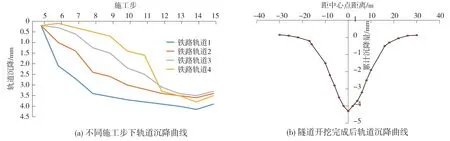
图12 不同施工步下及隧道顶进完成后轨道沉降曲线

由图11、图12 可知,随着隧道的开挖,轨道沉降越来越大;开挖完成时轨道地表路基中心点处沉降位移最大4.04 mm,施工时应采取相应控制措施避免轨道沉降过大对铁路运营的影响;从中心点竖向垂直于隧道方向两侧各监测点沉降量逐渐减小,至中心点两侧30 m 处沉降值为0.15 mm,开挖引起的沉降已经很小。

(2)隧道应力分析

开挖完成后,管片第一、三主应力云图见图13,顶进过程中管片各监测点的第一、三主应力变化曲线见图14。 由图13、图14 可知,隧道第一主应力表现为拉应力,最大值为1.80 MPa,隧道第三主应力表现为压应力,最大值为1.06 MPa。

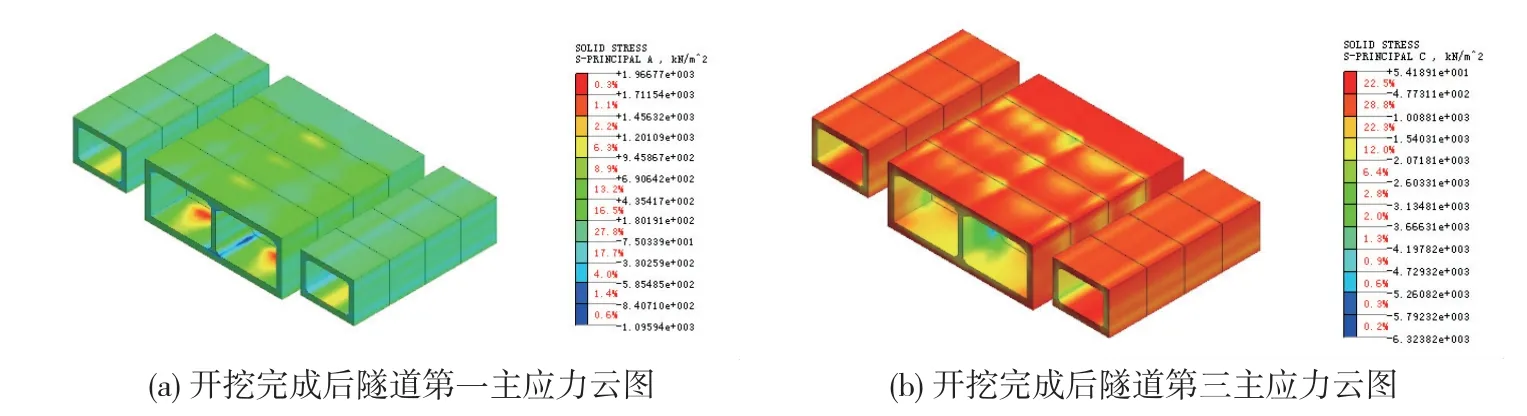
图13 开挖完成后隧道第一、三主应力云图

图14 不同开挖步下隧道第一、三主应力变化曲线

5 施工方法比较

矩形顶管法及管幕暗挖法比较见表5。

表5 矩形顶管法与管幕暗挖法比较

综上所述,结合本工程的实际情况,受两侧衔接道路限制,道路纵断面曲线半径较小,矩形顶管使用受到限制,并且矩形顶管掌子面前方封闭,不可控因素较多,同时顶管曲线顶进,管节之间的防水可靠性差,工期长,因此本工程首选管幕暗挖方案施工。

6 结论

以郑州火车站片区下穿运营铁路操场街隧道工程为研究背景,基于有限元数值模拟,分析矩形顶管法和管幕暗挖法施工过程中引起的运营铁路路基沉降变化,结论如下。

(1)轨道累计沉降量从隧道正上方中心点向两侧逐渐减小,管幕暗挖法施工主要影响范围为两侧20 m,矩形顶管法施工主要影响范围为两侧15 m。

(2)矩形顶管法施工轨道累计沉降值最大为5.6 mm,管幕暗挖法施工轨道累计沉降值最大为4.04 mm,均满足规范要求。

(3)比较顶管法施工与管幕法施工,无论哪种施工方法,轨道沉降最大处均为隧道正上方,隧道方向两侧沉降值呈对称分布。