突扩管中高分子聚合物溶液湍流减阻的数值模拟

石若冉，张浩，2，*，张志，李茂林

（1.山东建筑大学热能工程学院，山东 济南 250101；2.山东省绿色建筑协同创新中心，山东 济南 250101）

0 引言

供暖和制冷的实现建立在流体运输的基础上，流动带来的阻力不仅会增加能耗，而且会使管道壁面受到磨损，因而减少管道输运的阻力以达到节能性、经济性的目的一直是重要的研究方向。添加剂减阻指的是在管道流体中加入高分子聚合物或者表面活性剂来降低管道阻力的技术。早在1948 年，TOMS［1］就发现高分子聚合物可使湍流流动阻力大幅减小，该现象后被称为“TOMS”效应。自此学者们便开始了针对添加剂减阻方向的研究，为降低能耗和提高经济效益做出贡献。在实际工程应用方面，1979年聚合物减阻在美国阿拉斯加的石油输运行业中实现商业应用，在管道中添加减阻剂取得了良好的减阻效果［2］。为实现减阻节能，焦利芳等［3］开展减阻剂实际应用研究，在青岛某小区供热系统中加入表面活性剂十六烷基三甲基氯化铵／水杨酸钠（CTAC／NaSal），其效果理想［3］。这些应用实验充分证明了添加剂减阻技术实际应用方面的可行性，对其进行深入研究势必将在节能领域产生显著的经济效益。

针对添加剂减阻方式，学者们从流动特性、减阻机理等方面开展了研究，且随着计算机科学的发展，数值模拟也逐渐成为有力的工具。张红霞［4］分别利用纯黏性剪切稀化Carreau-Bird 模型与Giesekus黏弹性非牛顿流体本构方程模拟了CTAC 水溶液，探究其流动与减阻作用。李昌烽等［5］利用Cross模型模拟了聚丙烯酰胺（Polyacrylamide，PAM）溶液在二维轴对称圆管中的流场和温度场，分析了其减阻效果、传热性能。朱涵［6］采用Cross 模型分别模拟了减阻剂溶液的水下弹体与鱼形绕流减阻流动，分析了其减阻效果。李恩田［7］利用Carreau-Bird模型与幂律模型对CTAC减阻溶液、利用Cross流变模型对PAM溶液分别进行数值模拟，并结合壁面微沟槽探究了联合减阻。这些研究阐述了表面活性剂的减阻机理和规律，也充分证明了利用数值模拟研究减阻的可行性。

目前，关于添加剂减阻研究多数集中在直管，而实际管道系统中存在着很多种类的非直管管件，突扩管作为其中之一，其减阻研究在理论认识或实际工程应用都具有很高的价值。PAK 等［8］分析了聚丙烯酰胺AP-273水溶液在不同突扩比的突扩管中的局部阻力损失特性。POOLE 等［9］利用实验研究了不同浓度的聚丙烯酸（Polyacrylic Acid，PAA）溶液在面积比1∶4 突扩管中的湍流流动，探究了其流动的不对称性和再附着长度的变化。国内学者利用实验方法较多，且多数采用表面活性剂作为添加剂。焦利芳等［10］实验研究了CTAC／NaSal 减阻溶液在不同种类不规则管道（包括90°弯头、三通以及变径管）内的流动和减阻特性，发现其减阻效果比起直管段有着减弱现象。段传伟［11］利用实验法得到不同管径比的突扩管、突缩管中不同浓度的十六烷基三甲基溴化铵（Cetyltrimethylammonium Bromide，CTAB）溶液的流动，研究了压力分布、阻力发展长度、减阻效果等。蔡书鹏等［12-13］研究了管径比为1∶1.52及截面积比为1∶4 的突扩管中两种不同质量分数的CTAB水溶液的流动减阻行为，探究了局部阻力系数的改变及下游压力恢复长度等问题。王侃宏等［14］在管径比为1∶1.49 的突扩管中使用了3 种不同浓度CTAB水溶液，研究了上下游管道的沿程阻力系数以及突扩处的局部阻力系数的变化与减阻规律。

高分子聚合物和表面活性剂的主要不同之处在于，高分子聚合物起减阻作用的柔性长链结构相较于表面活性剂的胶束结构，前者在强剪切应力作用下会被破坏，且无法自我修复，而后者需达到一定浓度才可实现减阻，并且表面活性剂的添加会对管壁造成不利影响［15］。文章选择高分子聚合物PAM溶液作为研究对象，利用Cross模型描述其黏度变化，与纯水工况作对比，在管径比1∶1.5 的三维突扩圆管模型中分析其流场分布和不同雷诺数下直管段及突扩部分的减阻效果、回流区的变化。

1 数值模拟方法

1.1 几何模型

建立的突扩管模型如图1所示，设置上、下游管管径（d1、d2）分别为10、15 mm。为使得管内流体充分发展，两段管长分别设为20 倍自身管径长度，即上、下游管长（l1、l2）分别为200、300 mm。

图1 突扩管几何模型

1.2 数学模型

文章的流体流动研究不考虑传热，所需控制方程张量形式，即连续性方程和N-S 方程分别由式（1）和（2）［7］表示为

式中μ为流体动力黏度，Pa·s；p为压强，Pa；fi为流体质点的单位质量力，m／s2；ρ为流体密度，kg／m3。

湍流模型中的RNGk-ε模型适用于涡流的描述，对壁面的处理更准确。考虑到突扩管流动的特点，选其作为计算模型。RNGk-ε模型中湍动能（k）方程和湍动能耗散（ε）方程分别由式（3）和（4）［15-16］表示为

高分子聚合物减阻溶液属于非牛顿流体，相较于纯水而言，其溶液具有剪切稀化特性［7］，即黏度随着剪切速率的增加而减小，因此需要建立本构方程描述黏度。Cross 模型是其中一种用于描述非牛顿流体剪切稀化特征的流变模型，可由式（5）［18］表示为

式中λ为松弛时间，s；n为幂指数常数；μ0为零剪切黏度，Pa·s；为剪切速率，s-1。参考文献［7］和［18］的研究，为描述质量浓度为15 mg／L 聚丙烯酰胺溶液的动力黏度，参数μ0＝3.835 mPa·s、λ＝2.746 s、n＝0.7。

1.3 模拟设置

利用数值模拟法模拟突扩管中纯水和高分子聚合物PAM溶液的流动，二者物性参数设置如下：当模型工况为纯水时，动力黏度为0.001 kg／（m·s），密度为1 000 kg／m3；当模型工况为PAM溶液时，黏度描述采用Cross模型，而密度设置同纯水。

模拟采用三维稳态的方式，忽略重力影响；湍流模型选择RNGk-ε；边界条件中入口采用velocityinlet，通过设置入口平均速度大小实现不同雷诺数的湍流工况，出口采用pressure-outlet，壁面为无滑移条件。

2 网格无关性验证与可行性分析

2.1 网格无关性验证

突扩管几何模型的网格划分，因其结构较简单，采用适用圆柱体的o-block 结构化网格划分的方式。设置了网格数分别为42 万、96 万、121 万的3种网格，在雷诺数为10 000 的纯水工况下，对比突扩管中轴线上的静压分布，从而验证网格无关性。不同网格数目对应的静压分布如图2 所示，静压分布趋势一致，上游管在0 ～0.2 m 范围内下降至最小值，经突扩部分压力先上升后又呈下降趋势。在上游管段内，96 万与121 万网格的静压分布高度重合，压力恢复最大值也极为接近，可知42 万网格计算所得结果并不精准，网格数至96万再增加网格数量压力分布基本不再变化，因此选取96万网格进行计算，网格模型如图3所示。

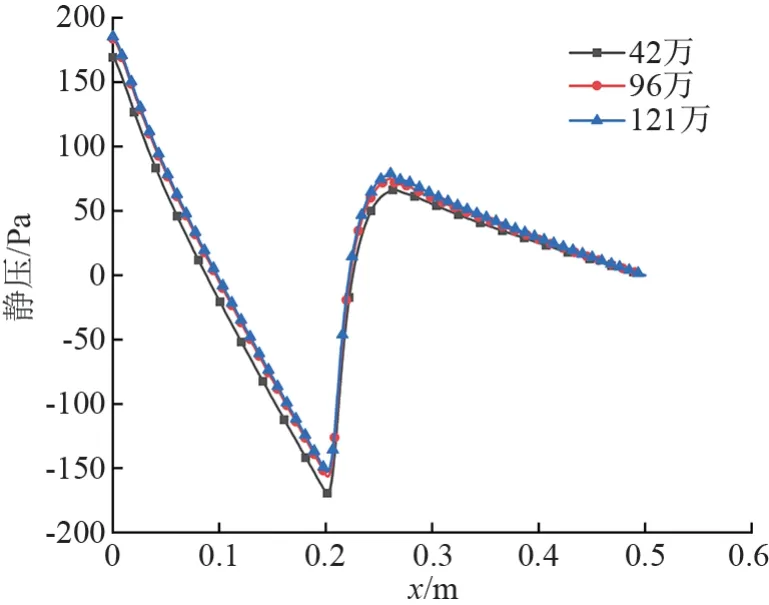
图2 不同网格数目静压分布

图3 突扩管网格模型

2.2 模拟合理性验证

为了验证模拟计算的正确性，在纯水工况下选取雷诺数在104～105范围计算上游管沿程阻力系数，并与布拉休斯经验公式所得结果进行对比。设置不同的入口速度调整雷诺数Re，其计算公式由式（6）［19］表示为

式中μs为纯水动力黏度，Pa·s；v1为上游管道平均流速，m／s。

文章相关分析皆以纯水工况上游直管雷诺数为依据。沿程阻力系数f由伯努利方程推导得出，由式（7）［13］表示为

式中Δp为两断面静压差，Pa；l为两断面距离，m。为保证管流充分发展且不受突扩处影响，选取距上游管入口处10d1、15d1两处的测压断面。

布拉休斯经验公式是计算牛顿流体沿程阻力系数的常用公式之一，适用于紊流光滑区、4 000＜Re＜100 000范围内，由式（8）［19］表示为

数值模拟结果与布拉休斯经验值对比如图4所示，两种沿程阻力系数的计算结果趋势一致，相对误差最大为5.6%，由此可得该模拟方法合理。

图4 沿程阻力系数对比

2.3 Cross模型准确性验证

流动介质为PAM溶液时，采用Cross模型描述其动力黏度。为验证Cross 模型准确性，建立60 mm×100 mm×1 000 mm 的槽道几何模型，参考文献［7］和［18］研究的结果，设置各参数取值λ＝5.491 s、n＝0.7、μ0＝9.835 mPa·s，描述质量浓度为60 mg／L的PAM胺溶液黏度，模拟计算的设置同1.3 节，得到范宁系数模拟值，与实验所得范宁系数［7］进行对比。范宁系数Cf由式（9）和（10）［4］表示为

式中τw为壁面平均切应力，Pa；H为槽道截面高度，取值为60 mm；W为宽度，取值为100 mm；Δpc为槽道充分发展流段所取两截面的静压差，Pa；L为两截面的间距，取值为200 mm；U为管段平均流速，m／s。

模拟中设置入口流速为0.553 6 m／s，通过模拟结果计算得到Cf＝0.002 99，与实验中相同流速下的范宁系数计算结果0.002 95 对比［7］，相对误差约为1.4%，证明Cross模型具有一定的准确性。

3 结果分析

3.1 突扩管流场分析

3.1.1 速度分布

纯水与PAM溶液在Re＝10 000 工况下的速度分布如图5所示。在模拟采用的突扩圆管模型中，两者的速度分布皆呈轴对称。由于流体与管壁之间产生的摩擦，上游直管段的速度呈现从中轴线位置沿径向向壁面减小的规律，并且上游整体流动几乎不受突扩的影响。经过突扩面，流速整体减小，在台阶处形成速度死区［20］，随着流动的发展，中轴线处速度下降至稳定，且速度死区逐渐消失，再次形成充分发展流；与上游管相比，下游管速度更小，这是由于管径增大导致的。速度死区的出现是因为在流体流动过程中，截面突然扩大，使得一部分流体从主流当中分离出去，产生回流现象，并且速度死区通常存在着涡旋［21］，为了消除涡旋，主流要提供能量，经突扩面后其流速就会降低。比较二者速度云图可以明显看出，当流动介质为PAM 溶液时，与纯水相比下游管近壁处的速度出现略微增大，表明PAM使得摩擦阻力减小，因而速度有所提高。

图5 Re＝10 000速度云图

3.1.2 压力分布

取管道中轴线上的静压值，无量纲化为压力系数Cp，其分布如图6所示。无量纲压力用中轴线各点静压与突扩面处的静压差与上游管动压之比由式（11）表示为

图6 不同工况下管道中轴线压力分布

式中pm、p0分别为中轴线各点、突扩面处的静压，Pa。

根据Borda-Canot 预测值计算式［9］，即2β2（1-β2），其中β为上下游管径比，得到压力恢复最大值约为0.494。纯水工况下，Re分别为40 000和60 000时，模拟所得压力恢复最大值分别为0.484、0.487，可见Re的变化对此值影响不大，与理论值相比误差最大约为2.0%，可知模拟较为准确。图6 中，上游管在0～20内的分布线斜率表示沿程阻力系数，下游管从压力恢复最大值处至40 的分布线斜率表示沿程阻力系数与管径比四次方的乘积，因管径比为定值，通过对比斜率可比较沿程阻力系数。

比较两种雷诺数的纯水工况可以看出，无论上游直管还是下游直管，Re＝40 000 时沿程阻力系数更大；Re＝60 000 时的压力恢复最大值出现的位置更靠后，说明回流区长度增加。比较相同雷诺数下纯水与PAM溶液的压力分布线，可以明显观察到加入PAM后直管中沿程阻力系数的减小，证明减阻效果的产生；同时PAM 溶液压力恢复最大值更大，且此值越大，说明回流区的涡旋损失减小［13］，因此可得PAM溶液中突扩处的局部阻力也表现出减阻效果，而相较于纯水工况，其压力恢复最大值的增加并不显著，可以推断局部阻力的减小幅度较小。另外，相同雷诺数下PAM溶液压力恢复最大值所处位置比纯水更靠后，说明减阻剂的加入使得回流区长度增加。

3.2 直管沿程阻力减阻分析

高分子聚合物溶液可实现管道湍流减阻，其直管中的减阻率可高达70%［7］。减阻率RD的计算公式由式（12）［12］表示为

式中fs、f′分别为纯水、高分子聚合物PAM 溶液的沿程阻力系数。

利用式（7）得到雷诺数分别为5 000、10 000、20 000、40 000、60 000、80 000、100 000 工况下的PAM溶液上游直管的沿程阻力系数，通过式（12）得到不同雷诺数下的上游直管减阻率，结果如图7所示。

图7 上游直管减阻率与雷诺数的关系图

随着雷诺数的增加上游直管段的减阻率呈现先增大后减小的趋势，其减阻率最大值约为26.2%，临界雷诺数约为20 000。出现这种减阻趋势的原因是，高分子聚合物的柔性链受剪切力的拉伸作用，使得其与湍流结构相互作用，降低湍流强度，对湍流涡旋产生抑制，产生了减阻效果，并在一定雷诺数范围内，拉伸作用加强而减阻效果增强，但是随着雷诺数继续增大，剪切力进一步的增强使得高分子聚合物结构无法承受其强度，主链和侧链开始断裂，其减阻率下降［7］。

最大减阻率数值较小的原因在于减阻效果与浓度有关［22］。此次模拟所参考的PAM溶液浓度未达到或已超出最佳浓度；另外，减阻流体的流变特性包括剪切稀化特性和黏弹性［4］，数值模拟中黏弹性的描述通过相关的黏弹性本构方程来实现，而模拟所使用到的Cross 模型用以描述其剪切稀化特性，未描述黏弹性，因此导致模拟得到的减阻率较小，同时也说明了使用Cross模型描述减阻溶液的局限性。

3.3 突扩局部阻力减阻分析

纯水中突扩管的局部阻力系数理论值ξ由式（13）［19］表示为

式中A1、A2分别为上、下游管的断面面积，m2。计算可得纯水工况局部阻力系数理论值ξ＝0.309。

计算纯水与PAM 溶液工况局部阻力系数模拟值时，采用伯努利方程［19］推导，得到式（14）和（15）

式中v2为下游管的平均流速，m／s；f1、f2分别为上、下游管的沿程阻力系数，计算时上游管两断面取距入口10d1与15d1处，下游管两断面取距突扩面10d2与15d2处；p1、p2分别为上、下游充分发展段中所取两断面1、2的静压，Pa；l10、l02分别为断面1 至突扩面的长度和突扩面至断面2的长度，m。

为综合分析突扩部分对管内上、下游整体减阻效果的影响，选定两组不同距离的断面，对比PAM溶液局部阻力系数。方案一的两处断面选定于突扩面前5d1和突扩面后10d2的位置；方案二的断面选定在突扩面前10d1和突扩面后20d2的位置。在Re为5 000至100 000的湍流流动范围内，局部阻力系数的结果如图8 所示。当流动介质为纯水时，局部阻力系数模拟值随着雷诺数的增大先减小后逐渐趋于稳定，其值在0.315 ～0.288间变化。PAM 溶液工况下，两种方案所得局部阻力系数的数值整体非常接近，相差最大不超过1.0%，可知即使上、下游断面距离不同，但整体减阻效果基本一致。局部阻力系数模拟值变化整体趋势表现为随着雷诺数的增大而增加，且未超出纯水工况的值，此与PAK 等［8］实验趋势一致，但增加幅度略小。雷诺数为100 000工况与纯水工况下的局部阻力系数已极为接近，PAM 溶液几乎失去减阻作用。在此次模拟的雷诺数范围内，突扩局部的减阻率最大约为10.8%，与直管中减阻率最大值（26.2%）相比，突扩局部的减阻效果不甚明显，分析其原因在于流体经突扩部分产生了涡旋，形成了回流区，剪切力随之增大，高分子聚合物的柔性链抵抗不住剪切而发生断裂，并且随着雷诺数增加，剪切力影响越发明显，局部阻力系数逐渐增大，导致减阻效果变差。

图8 局部阻力系数与雷诺数的关系图

3.4 回流区流动变化

回流区涡旋作为影响局部阻力的因素，其流动、能量变化的分析对了解减阻机理、实现突扩管减阻有着重要意义。将纯水、PAM溶液工况下所得回流区长度模拟结果通过Xr／h进行无量纲化表示，其中，Xr表示回流区长度，h＝（d2-d1）／2，所得结果见表1。无论是纯水还是PAM减阻溶液，回流区长度都是随着雷诺数的增加而增加；而在相同雷诺数下，PAM溶液的回流区比纯水中更长。减阻溶液中回流区长度增加，而依然表现出减阻效果。

表1 不同雷诺数下两种流体的回流区长度

湍动能云图如图9 所示。Re＝10 000 时，PAM溶液经突扩面后，台阶处的湍动能等值线密度较纯水明显变得稀疏，其最大等值线面积也明显变小，说明回流区内的湍动能有所减小，体现出了减阻效果。而从等值线形状可看出，湍动能最大处在回流区末端，对比相同数值的等值线，其在PAM 溶液中比纯水中在轴向上的位置靠后，说明此处湍动能轴向的减小变缓，PAM 使得湍动能沿轴向增加，因此导致回流区长度有所增长。

图9 不同雷诺数下的湍动能云图

由图9可知，雷诺数增大，流体的湍动能也随之增大，因而使得回流区长度增大。比较相同雷诺数下不同流体，可以观察到PAM 溶液相较于纯水，最大湍动能等值线面积皆有所减小，上游直管的壁面处湍动能也有着较为明显的下降，说明PAM对湍动能起到了抑制作用，且通过前面的分析已知两种雷诺数工况下都有减阻效果，可以推断这种抑制作用是实现减阻的原因。Re＝100 000 的工况下，PAM溶液与纯水的局部阻力系数最为接近。二者的湍动能云图分别如图9（c）与（d）所示，虽然最大湍动能值仍有减小，但台阶后的回流区处的等值线密度变化却并不明显，因此表现出局部阻力减阻效果的下降。

4 结论

文章利用Cross 模型描述高分子聚合物PAM溶液的黏度，模拟其在管径比为1∶1.5 的突扩管中不同雷诺数下的湍流流动，并于相同条件下的纯水工况做对比，分析了流场、减阻效果与回流区流动变化，得出结论如下：

（1）突扩管中的流动无论介质为纯水还是PAM溶液，经突扩面后都产生了速度死区；PAM 溶液压力恢复最大值大于纯水的，且出现位置靠后，说明涡旋损失有所减小且回流区长度增加。

（2）上游直管中随着雷诺数的增大，减阻率先增大后减小，其最大减阻率约为26.2%，临界雷诺数约为20 000。

（3）随着雷诺数的增加，纯水工况下的局部阻力系数先减小后趋于稳定，PAM溶液的局部阻力系数呈现增长的趋势，在模拟所设雷诺数范围内，后者数值未超过前者，PAM 溶液表现出减阻效果，但最大减阻率约为10.8%，较直管段减阻有较大幅度的下降。

（4）纯水与PAM 溶液的回流区皆随雷诺数的增加而伸长，相同雷诺数下PAM溶液中回流区长度更大，原因在于其末端处湍动能的轴向增加；相对于纯水，PAM溶液中湍动能最大值区域减小，PAM 对湍动能产生了抑制作用，表现出减阻效果。