Experimental Study on Generation and Evolution of Three-dimensional Freak Waves
,-
(National Engineering Research Center of Port Hydraulic Construction Technology,Tianjin Research Institute of Water Transport Engineering,Tianjin 300456,China)
Abstract:Freak waves can bring serious damage to vessels and maritime structures as well as to other facilities in the ocean due to the features of focused energy, strong nonlinearity, broad-banded spectrum, etc..Moreover such features are likely to be accompanied by other abnormal large waves occurring before or after them,such as deep troughs and successive large waves (wave group),which are also disastrous.Thus, more attention should be paid to both freak waves and associated abnormal large waves.In a real sea state,waves are usually characterized by multi-direction or short-crest.There are obvious differences between the dynamic behaviors of the two-dimensional and those of three-dimensional freak waves.Therefore,in this study,the complete generation and evolution processes of threedimensional freak waves are experimentally simulated through dispersive and directional focusing of component waves, in order to discuss the dynamic behaviors of the abnormal large waves occurring during the generation and evolution process as well as the relationships among them.The results suggest that the abnormal large wave evolves along the main wave direction in a symmetric way during the generation and evolution process of the three-dimensional freak wave, and that the process is divided into three or four typical stages based on characteristic parameters of abnormal large waves, implying that the variation trend of abnormal large waves can be predicted based on characteristic parameters.In the present study, the spatio-temporal range of the generation and evolution process is shorter for three-dimensional freak waves compared to two-dimensional events,the process for three-dimensional case may skip wave group stage and deep trough stage, implying that the likelihood of deep troughs and wave group associated with a freak wave in multidirectional random seas is likely to be small.
Key words:freak wave;rogue wave;generation and evolution;three-dimension;directional spread;multidirectional wave;experiment
0 Introduction
Freak waves or rogue waves are a type of independent large waves,which can appear suddenly in the open ocean all over the world.Such abnormal waves are commonly characterized by strong nonlinearity, short duration, focused energy and broad banded spectrum, which are likely to be accompanied by deep troughs and successive large waves (wave group)occurring before or after them.Due to the features mentioned above, these abnormal large waves can seriously damage vessels or offshore structures.
Generally,high waves often come together,forming a wave group.Gemmrich and Thomson[1]investigated the asymmetry of wave groups based on open ocean data.The degree of group asymmetry can be assessed by the relative position of the largest crest within a wave group.As pointed out,the asymmetry of wave groups is positively correlated with their nonlinearity and there is a clear trend of wave groups becoming asymmetric and the largest waves occurring closer to the beginning of the group with enhancing nonlinearity.Freak waves are uncharacteristically large compared to the surrounding sea state, exhibiting groupiness to a small degree in terms of the wave surface, but the strength of the groupiness, characterized by SIWEH-based groupiness factor, are great[2].It means that freak waves are likely to have relevance to wave groups.Stansell[3-4]reported that one hundred and four freak waves and one deep trough were obtained in analyzing the surface elevations measured during fourteen severe storms in North Sea,and that the deep trough with a depth of 5.38 m is 1.4 times the significant wave height, indicating that freak waves are likely to have relevance to deep troughs.The analysis of generation and evolution processes of two-dimensional numerical freak waves performed by Cui et al.[5]showed that the process was divided into seven typical stages based on characteristic parameters of abnormal large waves occurring during it, and that the deep troughs were likely to occur in the second and sixth stages.Further, the relevance of freak waves,deep troughs and wave groups was clearly identified.
Only in less-spread or unidirectional wave-fields,freak waves are likely to be characterized by long-crest, whereas in a real sea state, waves usually have three-dimensional characteristics ofshort-crest or broader directional spreading, which have significant influences on dynamic behaviors and characteristics of freak waves.In multi-directional wave-fields, freak waves exhibit differences in shape feature compared to unidirectional freak waves.In the numerical work of Fochesato et al[6], the three-dimensional freak waves show a curved wave front, followed by a deeper trough,with a crescent shape.Barratt et al[7]investigated the evolution of the steep, narrow-banded, directionally-spread, focusing wave group using the fully-nonlinear potential flow model, and pointed out that the third-order resonant interactions lead to the formation of wing waves at the periphery of the wave group, and the formation of broad, crescent shaped crests was attributed to the constructive interference between the wing waves and central crests.
The broadening directional spreading reduces the probability of a large wave event,correspondingly the distribution of wave height tends to fit better to the Rayleigh distribution[8],and also monotonically reduces the kurtosis of the surface elevation[9]due to weakening wave-wave interaction.Johannessen and Swan[10]indicated that the directional spreading can affect the nonlinearity of a large wave event due to the redistribution of the wave energy within the frequency domain.
The directional dispersion also affects the focal time and breaking characteristics, the increasing directional bandwidth leads to focused wave events steepening rapidly, limiting the total energy transfer and the growth in mean wave number[11].If the steep focused wave breaking occurs, the broadening directional spreading results in both greater breaking wave height and particle velocities at the crest.Two types of breaking waves had been showed.As can be seen, the first type is plunging breaking for the broader directional spreading cases, in contrast, the other type is spilling for the cases of narrower directional spreading[12].
Therefore,previous studies demonstrate that directional spreading is extremely important to accurately simulate freak waves and to explain their physical characteristics.Moreover most studies only concentrate on the variation of the freak wave itself, and little is known about the relevance of the three-dimensional freak wave to other abnormal large waves occurring during the generation and evolution process.Not only the freak wave but also the associated abnormal large waves are a significant threat to the ships or offshore structures.Thus,more attention should be paid to the relationship,based on which the evolution of abnormal large waves can be forecasted.
The superposition of component waves has been commonly used to explain the generation of freak waves.It had been addressed in many literatures that the experimental and numerical freak waves were successfully simulated based on the mechanisms[13-15].In this study, the whole generation and evolution processes of three-dimensional freak waves are simulated through dispersive and directional focusing of component waves in a wave basin.The freak wave is defined as a large wave withα1≥2,α2≥2,α3≥2 andα4≥0.65, whereα1=H0/Hs,α2=H0/H-1,α3=H0/H+1andα4=η0/H0,H0is the wave height of the large wave,η0is crest height of the large wave,H-1andH+1are the wave heights before and after the large wave[16].
The remainder of the study is organized as follows.Firstly,we review the results for the generation and evolution process of two-dimensional numerical freak waves[5].Then the conclusion is well confirmed by the present experimental results, furthermore, detailed analysis is presented.And then this is followed by a detailed study of the variation in characteristics of abnormal large waves occurring during the generation and evolution process of three-dimensional freak waves, and the relevance of three-dimensional freak waves to other abnormal large waves based on experimental results.In conclusion, we discuss the differences in the generation and evolution process between two-dimensional freak waves and three-dimensional ones.
1 Experimental arrangements
Fig.1 shows a sketch of the flume in which the two-dimensional experiments were implemented.The facility is 56 m long and 1.0 m wide with a water depth of 0.5 m.A piston-type wave maker is installed at one end of the flume, and an artificial absorbing beach is located at the opposite end to dissipate the reflected wave energy.And the wave surface elevations are measured by an linear array of 32 wave gauges aligned with the direction of wave propagation,with a spacing of 20 cm between adjacent gauges.
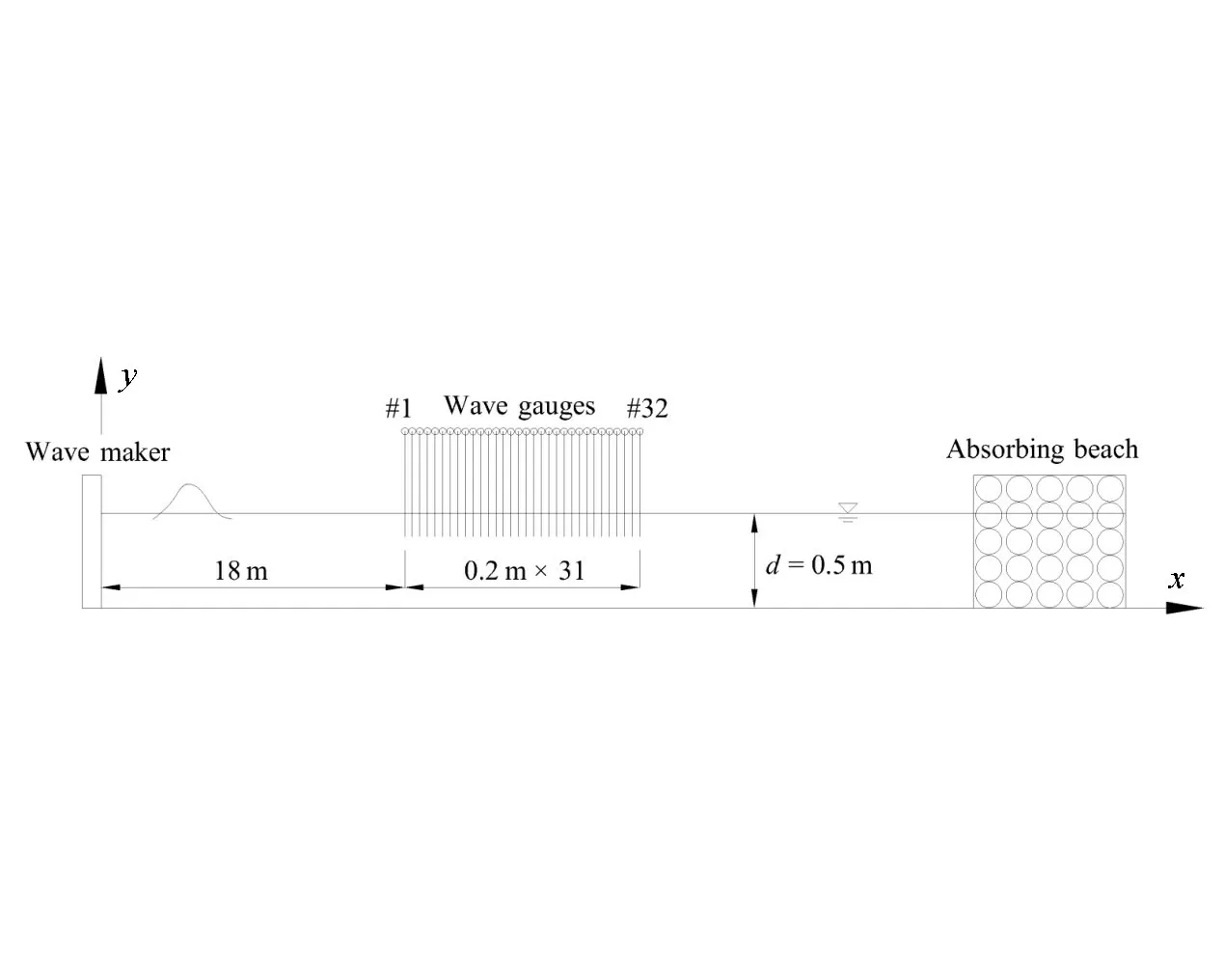
Fig.1 Sketch of the wave flume and wave gauge locations for two-dimensional experiments
The present three-dimensional experiments were carried out in a 55 m×34 m wave basin with a water depth of 0.4 m.The three-dimension waves are generated through 70 wave paddles located along one of the shorter sides of the basin,and each paddle is 0.4 m in width.The artificial absorbing beaches are installed at the other sides to minimise the reflected wave energy.A linear array of 18 wave gauges are set up along the main direction of wave propagation for measuring the wave surface elevations.The schematic illustration of the wave basin is depicted in Fig.2.The upper panel is the top view and the lower panel is the vertical slice taken atz=0.5lwm=14 m,wherelwmis the length of the wave maker.

Fig.2 Sketch of the wave basin and wave gauge locations for three-dimensional experiments
In this study, the wave maker signal generation is based on the dual-superposition model, in which the total wave energy spectrum is split into two parts: one for the background random waves and the other for the transient wave[17].The frequency spectrum is defined as a modified P-M spectrum expressed as:
whereHsis the significant wave height andTaveis the average period.
The directional spreading function is expressed as:
where 2n!!=2n×(2n-2)×...×4×2,(2n-1)!!=(2n-1)×(2n-3)×...×3×1.The coefficientnis taken to be 2 in the present study.According to the experimental arrangements, the angle of main wave direction is zero.The directional spectrumS(ω,θ) is defined as the product of the frequency spectrumS(f)and the directional spreading functionG(θ).
The dispersive and directional focusing mechanism is commonly used to explain the generation of freak waves.In order to increase focusing efficiency, herein, the dual-superposition approach is used to generate freak waves,i.e.a set of wave components that focuses at a given point in time and space are added to a background random sea.The dispersive and directional focusing occurs as a result of designed coherent phase distribution,i.e.at the spatio temporal focusing point,focused wave components with identical phase 0 produce crest focusing.
For two-dimensional events,the surface elevation of the freak wave is given by
For three-dimensional cases,the surface elevation of the freak wave is estimated as Eq.(4),extending Eq.(3)to incorporate the effect of directionality.
whereηis the surface elevation;dis the water depth;tcis the focusing time;xcandzcare the horizontal coordinates of focusing position;a1i=(2p1S(f)Δf)1/2anda2i=(2p2S(f)Δf)1/2are the amplitudes of the random and transient component waves for two-dimensional cases;a1mi=(2p1S(ωm,θi)ΔωΔθ)1/2anda2mi=(2p2S(ωm,θi)ΔωΔθ)1/2are the amplitudes of the random and transient component waves for three-dimensional cases;the energy of the target spectrum is divided intoMbands in frequency domain,and the directional anglesθiare uniformly distributed in the range of-π/2~π/2;ωmandkmdenote the angular frequency and wave number of each component wave,respectively,and are related by the linear dispersion relation;εis the random phase distributed in the range of 0~2π;p1andp2are the proportions of the energy of the random and transient trains, respectively.For two-dimensional cases,p1andp2are taken to be 80% and 20%[18],p1andp2are taken to be 97% and 3% for three-dimensional cases.
Based on linear wave-maker theory, the strokeS0(t) can be written as Eq.(5) for two-dimensional cases and as Eq.(6)for three-dimensional cases.
whereη1i(t)=cos(km x0-ωm t+εm),η2i(t)=cos(km(x0-xc)-ωm(t-tc)),Wm=4sinh2kmd/sinh2kmd+2kmdis the transfer function associated with the component wave,x0is horizontal coordinate of the wave maker.
whereη1mi(t)=a1micos(km(x0cosθi+z0sinθi)-ωmt+εmi),η2mi(t)=a2micos(km(x0-xc)cosθi+km(z0-zc)sinθi-ωm(ttc)),Wmi= 4sinh2kmd/(sinh2kmd+2kmd)cosθiis the transfer function associated with the component wave,x0andz0are horizontal coordinates of the wave maker.
In this study, the freak wave is defined as a large wave withα1≥2,α2≥2,α3≥2 andα4≥0.65,
whereα1=H0/Hs,α2=H0/H-1,α3=H0/H+1andα4=η0/H0,H0is the wave height of the large wave,η0is crest height of the large wave,H-1andH+1are the wave heights before and after the large wave[16].
In the following chapters,the study of the generation and evolution processes of freak waves is implemented based on one two-dimensional and six three-dimensional freak waves simulated in the present facilities.
2 Results and discussion
2.1 Generation and evolution of two-dimensional experimental freak waves
Cui et al[5]made a detailed study of generation and evolution processes of two-dimensional freak waves based on numerical results.In their study, abnormal large waves are defined as waves withα1≥2,which occur during the generation and evolution process of the freak wave,moreover,according to the parameter criteria that the abnormal large waves meet, the generation and evolution process of the two-dimensional freak wave is divided into seven typical stages.
In order to further examine freak waves and the relationship to other abnormal large waves in two-dimensional wave-fields,a two-dimensional freak wave is experimentally simulated by dispersive focusing in the wave tank and the features of the abnormal large waves occurring during the generation and evolution process of the freak wave are observed in the present study.The normalized surface elevations of abnormal large waves are shown in Fig.3.The surface elevation records are normalized by the significant wave height (Hs).Times are defined relative to the focus time (tc),normalized by the characteristic period (Ts).The abnormal large waves are highlighted by using red and blue lines for zero-up and zero-down crossing analysis,respectively.
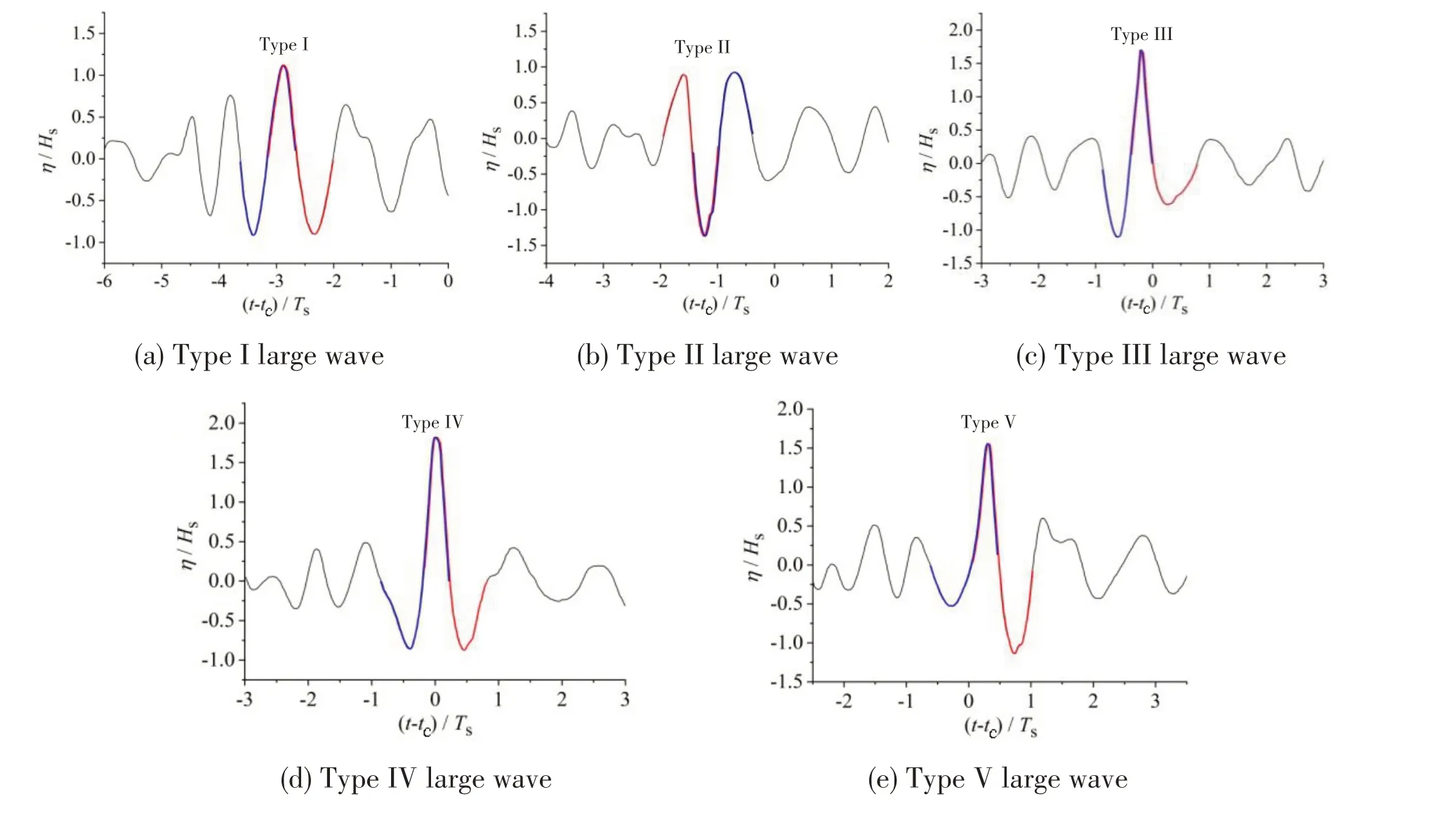
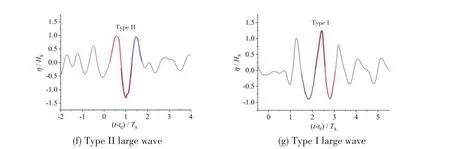
Fig.3 Normalized surface elevations of abnormal large waves occurring during the generation and evolution process of a two-dimensional freak wave
The present experimental results are consistent with the numerical results[5].The generation and evolution process of the two-dimensional experimental freak wave also has seven typical stages during which five typical abnormal large waves appear, and the abnormal large wave evolves in a symmetrical way.
In the first stage, the maximum wave with onlyα1≥2, comes together with adjacent high waves to form a wave group or successive large waves (see Fig.3(a)), also referred to as‘three sisters’[19];then in the second stage, the maximum wave withα1≥2 andα2≥2, appears in the form of a deep trough (see Fig.3(b)), also called‘hole in the sea’[3-4]; then in the third stage, the maximum wave withα1≥2,α3≥2 andα4≥2,appears in the form of an independently large wave,and there is a deeper trough prior to the wave crest (see Fig.3(c)); then in the fourth stage, the maximum wave withα1≥2,α2≥2,α3≥2 andα4≥2, meets all the freak wave criteria, forming a freak wave (see Fig.3(d));then in the fifth stage, the maximum wave withα1≥2,α2≥2 andα3≥2, appears as an independently large wave, and there is a deeper trough after the wave crest (see Fig.3(e)); then in the sixth stage,the maximum wave withα1≥2 andα2≥2 meets the same parameter criteria as the second stage, appearing as a deep trough (see Fig.3(f)); finally, in the seventh stage, the maximum wave with onlyα1≥2 meets the same parameter criteria as the first stage, coming together with adjacent high waves to form a wave group (see Fig.3(g)).It should be noted that the freak wave parametersα1,α2,α3andα4are calculated from the zero-up crossing analysis of surface elevation records (a wave starts from the zero-up crossing point of wave surface,and the period is defined as the distance between two zero-up crossing points on the time axis).Generally,the abnormal large wave is likely to pass through all the seven typical stages during focusing and defocusing, and sometimes may skip one or more typical stages.
Further, during the generation and evolution process, as the abnormal large wave evolves, the largest wave does not always follow a gradual buildup,the wave adjacent to the largest wave may develop into a new largest wave due to zero-crossing analysis limitation rather than a physical phenomenon, such as if the zero-up crossing analysis method is used to estimate the wave height(crest-trough), the abnormal large wave has a deep trough in the second stage (see Fig.3(b)), and then, following the second stage, the gradual increasing of the crest behind the deep trough will tend to form a new largest wave withα1≥2,α3≥2 andα4≥2 instead of the front wave.In the third stage, as a result of the evolution of the deep trough, the trough in front of the largest crest is still deeper than the back one (see Fig.3(c)), however the wave height of the abnormal large wave is calculated from the shallower trough value based on zero-up crossing analysis,thus the wave height of the abnormal large wave is likely to be underestimated.Similarly,due to the symmetry of the generation and evolution process, the wave height of the abnormal large wave in the fifth stage may also be underestimated based on zero-down crossing analysis.
In order to better describe the characteristics of abnormal large waves, both zero-up crossing and zero-down crossing analysis are used to estimate the freak wave parameters ofα1,α2,α3andα4in the present study.The subscripts‘-up’,‘-down’denote the zero-up crossing and zero-down crossing analysis respectively.
In the first and seventh stages, the abnormal large wave meets onlyα1-up≥2 orα1-down≥2, called Type I large wave for the sake of convenience (see Fig.3(a) and Fig.3(g)); in the second and sixth stages, the abnormal large wave meetsα1-up≥2,α2-up≥2 orα1-down≥2,α3-down≥2, called Type II large wave (see Fig.3(b) and Fig.3(f)); in the third stage, the abnormal large wave meetsα1-up≥2,α3-up≥2,α4-up≥2 orα1-down≥2,α2-down≥2,α3-down≥2, called Type III large wave (see Fig.3(c)); in the fourth stage,the abnormal large wave meetsα1-up≥2,α2-up≥2,α3-up≥2,α4-up≥2 orα1-down≥2,α2-down≥2,α3-down≥2,α4-down≥2,being a freak wave,also called Type IV large wave(see Fig.3(d));in the fifth stage,the abnormal large wave meetsα1-up≥2,α2-up≥2,α3-up≥2 orα1-down≥2,α2-down≥2,α4-down≥2, called Type V large wave (see Fig.3(e)).Tab.1 presents the freak wave parameters of the abnormal large waves based on both zero-up crossing and zero-down crossing analysis.

Tab.1 Freak wave parameters of abnormal large waves for the two-dimensional freak wave
The difference between parameters calculated from zero-up crossing and zero-down crossing analysis is significant for the third and fifth stages due to the great difference between trough values in front of and behind the high crest,it means that,to better describe the characteristics of Types III and V large waves, both front and back troughs should be considered, thus only one type of zerocrossing analysis is not enough to accurately depict the generation and evolution process.In contrast,the difference is slight for the initial and late stages,implying that there is marginal difference in the span (range of positions) and persistence of the process based on zero-up crossing analysis,relative to zero-down crossing analysis.
2.2 Generation and evolution of three-dimensional experimental freak waves
According to the parametersα1,α2,α3andα4of abnormal large waves, the generation and evolution process of the three-dimensional freak wave is divided into different typical stages which resembles the two-dimensional event.The definition of abnormal large waves for three-dimensional case is the same as that for two-dimensional case.Tab.2 lists the freak wave parameters of the abnormal large waves occurring during the generation and evolution processes of the three-dimensional freak waves for six experimental cases, wheretmdenotes the time of the deep trough for Type II large wave, or the time of the large wave crest for other typical large waves;xmdenotes the position of the abnormal large wave;Tsis the significant period;the associated characteristic wavelength (Ls)follows the linear dispersion relation.It should be noted that both zero-up crossing and zero-down crossing parameters are calculated.The normalized surface elevations of abnormal large waves for Cases 1-4 are shown in Figs.4-7.The surface elevation records are normalized by the significant wave height (Hs), and times are defined relative to the time of freak wave crest (tc), normalized by the characteristic period(Ts)for each case.

Tab.2(a) Freak wave parameters of abnormal large waves for three-dimensional cases based on zero-up crossing analysis

Tab.2(b) Freak wave parameters of abnormal large waves for three-dimensional cases based on zero-down crossing analysis
Fig.4(a) shows Type II large wave; Fig.4(b) shows Type III large wave; Fig.4(c) shows Type IV large wave (freak wave);Fig.4(d)shows Type V large wave based on zero-down crossing analysis or Type IV large wave (freak wave) based on zero-up crossing analysis, if the process is described by zero-down crossing parameters, it reaches its last stage, but not by zero-up crossing analysis;Fig.4(e)shows Type V large wave based on zero-up crossing analysis,whereas the target wave does not meetα1-down≥2 based on zero-down crossing analysis.
Fig.5(a) shows Type III large wave; Fig.5(b) shows Type IV large wave (freak wave); Fig.5(c)shows Type V large wave, if the process is described by zero-down crossing parameters, it reaches its last stage,but not by zero-up crossing analysis;Fig.5(d)shows Type V large wave based on zeroup crossing analysis, whereas the target wave does not meetα1-down≥2 based on zero-down crossing analysis.

Fig.5 Normalized surface elevations of abnormal large waves occurring during the generation and evolution process of the three-dimensional freak wave for Case 2
Fig.6(a) shows Type II large wave based on zero-down crossing analysis, whereas the target wave does not meetα1-up≥2 based on zero-up crossing analysis; Fig.6(b) shows Type III large wave;Fig.6(c)shows Type IV large wave (freak wave);Fig.6(d)shows Type V large wave,if the process is described by zero-down crossing parameters, it reaches its last stage, but not by zero-up crossing analysis; Fig.6(e) shows Type V large wave based on zero-up crossing analysis, whereas the target wave does not meetα1-down≥2 based on zero-down crossing analysis; Fig.6(f) shows Type II large wave based on zero-up crossing analysis, whereas the target wave does not meetα1-down≥2 based on zero-down crossing analysis.
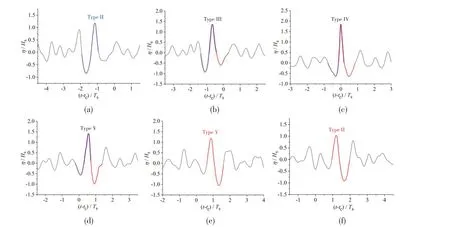
Fig.6 Normalized surface elevations of abnormal large waves occurring during the generation and evolution process of the three-dimensional freak wave for Case3
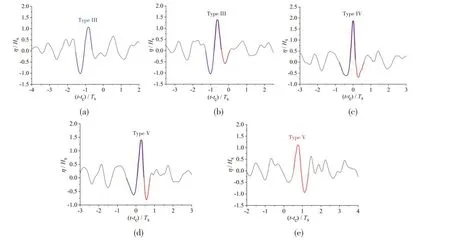
Fig.7 Normalized surface elevations of abnormal large waves occurring during the generation and evolution process of the three-dimensional freak wave for Case 4
Fig.7(a) shows Type III large wave based on zero-down crossing analysis, whereas the target wave does not meetα1-up≥2 based on zero-up crossing analysis; Fig.7(b) shows Type III large wave;Fig.7(c)shows Type IV large wave (freak wave);Fig.7(d)shows Type V large wave,if the process is described by zero-down crossing parameters, it reaches its last stage, but not by zero-up crossing analysis; Fig.7(e) shows Type V large wave based on zero-up crossing analysis, whereas the target wave does not meetα1-down≥2 based on zero-down crossing analysis.
It is observed experimentally that the abnormal large wave evolves along the main wave direction during the generation and evolution process of the three-dimensional freak wave.In the initial stage, the abnormal large wave meetsα1-up≥2,α2-up≥2 orα1-down≥2,α3-down≥2, appearing as Type II large wave for Case 1 and Case 3, or meetsα1-up≥2,α3-up≥2,α4-up≥2 orα1-down≥2,α2-down≥2,α3-down≥2,appearing as Type III large wave for Case 2, Case 4, Case 5 and Case 6.Unlike two-dimensional case,there is no Type I large wave in the initial stage,the abnormal large wave in multi-directionalwave-fields may just skip one or two stages and go directly to the second or third stage due to lower degree of the wave energy focusing in the main wave direction.
Following the second stage, evolution of the abnormal large wave exhibits an increasing trend in the crest behind the deep trough and a reduction in the deep trough,which may produce Type III large wave as the third stage.Then the qualitative trend is consistent, and the trough value in front of the large crest gets close to the back one,resulting in a freak wave during the evolution of the abnormal large wave reaching the fourth stage.After freak wave, the abnormal large wave appears as Type V large wave,which is likely to be higher than freak wave in its infancy due to the continuous increase in the back trough value, and then as the back trough continues to get deeper, the crest gradually reduces, the abnormal large wave degenerates into Type II large wave again.As the late stage of the process,the abnormal large wave may appear as a Type II large wave for Case 3,Case 5 and Case 6 or a Type V large wave for Case 1, Case 2 and Case 4 depending on the degree of the wave energy focusing in the main wave direction.The process does not include the seventh stage different from the two-dimensional case.
It can be seen that the generation and evolution process of the three-dimensional freak wave includes three or four typical stages, and that similar to two-dimensional freak waves, the abnormal large wave also evolves in a symmetric manner during the focusing and defocusing.
If the process starts at the third stage, there may be an upstream shifting of the position, in which Type III large wave occurs, based on zero-down crossing analysis due to the deeper front trough.It implies that the process described by zero-down crossing analysis may start earlier compared to zero-up crossing analysis (see Fig.7(a) and Fig.7(b)), in contrast, if the process ends at the fifth stage, there may be a downstream shifting of the position where Type V large wave appears based on zero-up crossing analysis due to the deeper back trough.It implies that the process described by zero-up crossing analysis may end later than zero-down crossing analysis (see Fig.4(d)and Fig.4(e); Fig.5(c) and Fig.5(d); Fig.7(d) and Fig.7(e)).The difference suggests that combining both types of zero-crossing analysis methods would be required to completely describe the generation and evolution process of the three-dimensional freak wave.
For all six three-dimensional cases,the persistence of the typical generation and evolution process from zero-up crossing analysis is about 1.2-2.7 times the significant period (Ts), during which the abnormal large wave spans about 0.8-2.1 times characteristic wavelength (Ls).The persistence from zero-down crossing analysis is about 0.2-2.5 times the significant period (Ts), during which the abnormal large wave spans about 0.2-1.9 times characteristic wavelength (Ls).The persistence based on combining both types of zero-crossing analysis is about 1.2-3.3 times the significant period (Ts), during which the abnormal large wave spans about 0.8-2.4 times characteristic wavelength(Ls).In contrast,according to Ref.[5],for two-dimensional freak waves,persistence of the generation and evolution process from zero-up crossing analysis is about 5-15 times the significant period(Ts),during which the abnormal large wave spans about 3-7 times characteristic wavelength(Ls).
The differences in persistence and span (range of positions) for three-dimensional cases, relative to two-dimensional cases, are remarkable.Since the component waves can spread directionally, and as a result, the wave energy focusing due to dispersion, is diminished in the main wave direction, in contrast, the higher degree of wave energy focusing occurs in the vicinity of the freak wave.
It is generally recognized that parameters ofα1andα4which characterize the wave itself are important to a large wave,even some researchers only useα1(orα1andα4)to define freak waves without regard toα2andα3, whereas, the present study suggests thatα2andα3are also interesting parameters that can describe the relationship between the large wave and the adjacent waves,and can be used to predict the evolution of abnormal large wave together with parameters ofα1andα4.
In addition, there is a major effect of wave breaking on the generation and evolution process,the experimental results show that the wave height loss due to wave breaking may result inα1<2.If the target wave does not meetα1≥2,the process is disturbed.
3 Conclusions
The generation and evolution processes of two-dimensional and three-dimensional freak waves formed experimentally by dispersive and directional focusing were investigated.
The present two-dimensional experimental results are in concordance with the published numerical results.For three-dimensional cases, an abnormal large wave evolves along the main wave direction during the generation and evolution process, which is divided into three or four typical stages based on the characteristic parametersα1,α2,α3andα4.With features similar to those of two-dimensional cases, the shape of the abnormal large wave varies in a symmetric manner, and there is a close relationship among the abnormal large waves.The relationship allows us to predict the variation trend of abnormal large waves with respect to the shapes or parametersα1,α2,α3andα4implying thatα2andα3can indirectly characterize an abnormal large wave,and thus are also important parameters.
In order to better characterize an abnormal large wave, both zero-up and zero-down crossing analysis methods are adopted to estimate the characteristic parameters.Unlike a two-dimensional case, the generation and evolution processes of three-dimensional freak waves starts at the second or third stage of the evolution of the abnormal large wave,and ends at the fifth or sixth stage.Based on six cases of three-dimensional experimental events, the duration of the process is about 1.2-3.3 times the significant period (Ts), during which the abnormal large wave spans about 0.8-2.4 times characteristic wavelength(Ls).
Directional spreading can reduce wave energy focusing in the main wave direction,in contrast,the higher degree of wave energy focusing occurs in the vicinity of the freak wave,which can lead to a reduced persistence of the generation and evolution process,implying that successive large waves(Type I large wave)and deep troughs(Type II large wave)are likely to be rarer occurrences of directional random seas,compared to unidirectional or narrow directional random seas.
- 船舶力学的其它文章
- A Numerical Study of Wave-Structure Interactions for a Square Structure with Different Submerged Depths
- Numerical Simulation of Two Degrees Coupled Sloshing of Distributed Liquid Tanks in Ships
- Freezing Process Simulation of Standing Water Droplets Under Different Supercooling and Contact Angles
- Load-bearing Characteristic Analysis of Marine Sandwich Composite Structures with Bi-modulus
- Analysis on Plastic Responses of Metal Foam Sandwich Beams under Low Velocity Repeated Impacts
- An Improved Prediction Method for Structural Response Analysis of Offshore Wind Turbines

