Analysis on Plastic Responses of Metal Foam Sandwich Beams under Low Velocity Repeated Impacts
-,-,,-
(1.Key Laboratory of High Performance Ship Technology(Wuhan University of Technology),Ministry of Education, Wuhan 430063, China; 2.School of Naval Architecture, Ocean and Energy Power Engineering, Wuhan 430063, China; 3.Key Laboratory of Impact and Safety Engineering,Ministry of Education,Ningbo University,Ningbo 315211,China)
Abstract:This paper presents the repeated impact tests of a metal foam sandwich beam(MFSB)by using INSTRON 9350 drop tower and analysis of the deformation and energy absorption performance of the MFSB.Based on the rigid-plastic assumption, the theoretical model is established to analyze the plastic mechanical behavior of an MFSB suffering from repeated low velocity impacts, in which the bounds of dynamic solution of permanent deflection are derived.The theoretical predictions are compared with the results of impact tests.Results show that the displacement of the sandwich beam is linearly distributed, and the deflection increases with the impact number, while the increment declines.With the increase of the impact number, the plastic deformation energy produced in each impact decreases while the rebound energy increases.The permanent deflections predicted by theoretical solutions agree well with those obtained from the impact tests, confirming that the theoretical model is capable of predicting the plastic responses of MFSBs subjected to repeated impacts.The proposed analytical model can provide theoretical references and technical supports for the design of the MFSBs under repeated impact loadings.
Key words:metal foam sandwich beam;repeated impact;plastic response;impact test;theoretical analysis
0 Introduction
When marine structures are subjected to repeated impact loadings during navigation and operation, such as from supplying ships, dropped objects, floe ice and so on, the deformation and damage will accumulate, resulting in failure and damage of the structures, even causing serious accidents[1].Hence, it is critical to study the dynamic behavior of marine structures under repeated impacts.
Attention was paid to the problem on repeated collisions of ships by Zhu[2]first in 1990,the dynamic responses of ship plates suffering from repeated impacts with a rigid mass were investigated by theoretical analysis, numerical simulation and impact tests.In Zhu's study, the numerical program was developed based on finite deference method to predict the permanent deflection of ship plates.To further study the dynamic behavior of ship plates subjected to repeated impacts, the repeated collision tests on rectangular plates with fixed boundary were conducted,and the correlation between permanent deflections and impact number was obtained[3].Afterwards,the theoretical model based on rigid-plastic assumption was established to analyze dynamic plastic mechanism of rectangular plates under repeated impacts, and the theoretical formula of permanent deflections were derived.In recent years,a series of works were carried out by Zhu and his co-workers[4-7]on the dynamic responses of ship plates suffering from repeated impact loadings.Firstly, a theoretical analysis was performed to study the plastic behavior of ship plating subjected to repeated impacts from floe ices,and the expressions were obtained to predict the permanent deflections.Then,the mechanism of damage accumulation of stiffened plates under repeated impacts was investigated experimentally and theoretically, and the correlation of stiffness, rebound velocity and elastic energy etc.with impact number were revealed.
As a new type of lightweight material, metal foam has excellent mechanical properties, and its sandwich structure has structural and mechanical advantages[8-9].As protective structures, metal foam sandwich structures possess potential applications in the field of naval and ocean engineering for improving their load-carrying capacity,impact protection and structural integrity.
Recently, some researches have been studying the dynamic behavior of MFSBs under single impact loadings[10-12].The experimental investigation was performed by Jing et al[13]to study the dynamic responses of a metal foam sandwich beam suffering from impact of aluminum foam bullet.In that work,high speed camera was used to record the impact process,and the deformation mode and failure mode of the sandwich beam were discussed.In order to determine the dynamic responses of metal foam sandwich beams subjected to blast loadings, a rigid plastic theoretical model was proposed by Qin[14]based on rigid,perfect plastic assumption,and the analytical formula of dimensionless deflection were derived.In addition,the bounds solutions of the permanent deflection were also adopted based on the circumscribing and inscribing yield locus.Afterwards, the theoretical model on metal foam sandwich beams suffering from low velocity mass impact was given, in which the results obtained from quasi-static and dynamic analysis were compared[15].
Numerous studies have been published on the mechanical behavior of metal foam sandwich beams under impact loadings, while little attention has been paid to the structural response under repeated impacts.The mechanism of deformation accumulation and energy dissipation of metal foam sandwich structures have remained unrevealed.In this paper, to examine the dynamic plastic responses of metal foam sandwich beam subjected to repeated low velocity impacts,the repeated impact tests on MFSBs were first performed using INSTRON 9350 drop tower.Then,a theoretical analytical model was established based on rigid plastic assumption.In the theoretical model,the bounds solutions of the deflection were derived using the circumscribing and inscribing yield locus.Finally,the theoretical model was verified by comparing the permanent deflections with those obtained from the impact tests.
1 Experimental study
1.1 Experimental setup
The repeated impact tests were performed by using INSTRON 9350 drop tower, as shown in Fig.1.Since the top of the additional mass frame was connected with a spring acceleration system,the initial impact velocity could be larger than that of free drop,and the maximum velocity could reach 24 m/s.
As seen from Fig.2, the MFSB was clamped at two ends with bolts to provide a fixed boundary.As shown in Fig.3, the impactor with a wedge nose was connected to a force transducer which had a maximum capacity of 90 kN,and the sampling frequency was 500 kHz.During the impact test, all the data were transferred from the force transducer by a data acquisition system (DAS 64K).Thus, the time history of velocity could be converted from the time history of impact force.
The MFSB was composed of front face sheet,back face sheet and an aluminium foam core,and the face sheets and core were glued by epoxy resin.Thicknesses of the face sheets and core weret=1 mm andc=10 mm,respectively.The span of the sandwich beam wasLS=150 mm,and the width of beam wasB=30 mm.In the repeated impact tests of the MFSB, the impact mass was 7.884 kg,the initial impact velocity was 2.12 m/s,so the impact energy was 17.8 J.
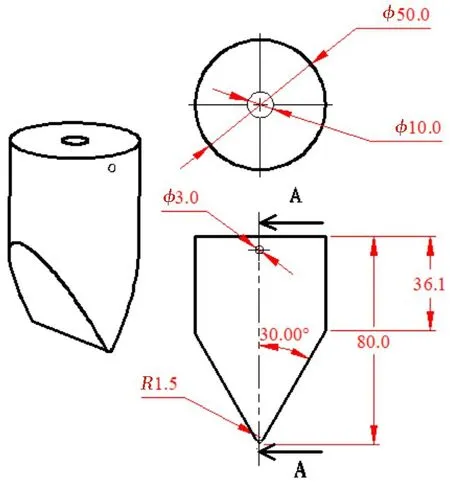
Fig.3 Dimensions of impactor
1.2 Experimental results
In this study,the bolts were used to constrain the ends of the sandwich beam.The deformation profile of the MFSB in the 10th impact is presented to discuss the deformation mode of the beam under repeated impact tests, as plotted in Fig.4.It can be found that when suffering low velocity impact,plastic hinges formed at the middle span and the boundary of the sandwich beam,and the deformation was almost linearly distributed from the middle span to the two ends.The external impact energy was mainly consumed by the plastic moment and axial force,in the form of plastic hinge rotation and axial elongation.

Fig.4 Deformation profile of MFSB
The impact test was repeated with same energy of 17.8 J, neither the face sheet nor the metal foam core experienced fracture in the first 10 impacts.As the impact number increased, the absorbed energy increased, leading to the deformation of the MFSB being enlarged gradually, as shown in Fig.5.During the repeated impacts, for all impacts, the deformation profile of the MFSB exhibited symmetry, the displacement approximately exhibited linear distribution, and the plastic hinges were located at the middle span and the fixed ends.Thus, the relevant assumptions on the deformation mode and energy consumption can be proposed in the theoretical model for low velocity repeated impacts.

Fig.5 Deformation profile of MFSB under repeated impacts
The time history of impact force of MFSB is plotted in Fig.6, from which it can be found the peak value of impact force increased with the impact number, and the duration time of the impact decreased.
As illustrated in Fig.7,the impact velocity increased with the increase of impact time,once its value declined to be zero, the impact velocity increased in the opposite direction till the impactor was separated from the surface of the MFSB.As the impact number increased,the rebound velocity increased gradually.

Fig.6 Time history of impact force of MFSB

Fig.7 Time history of impact velocity of MFSB
During the repeated impacts, the absorbed energy would accumulate with the increase of impact number.As shown in Fig.8, as the impact number increased, the permanent deflections of the face sheets increased,while the increment declined.
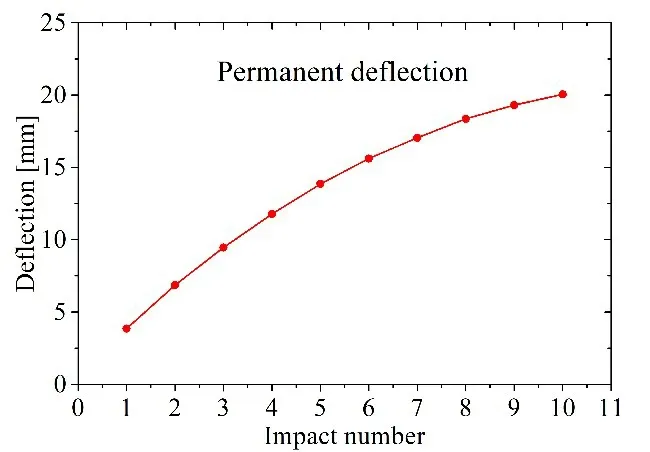
Fig.8 Permanent deflection of MFSB
The energy consumed by the MFSB could be divided into two major parts,i.e.plastic deformation energy and elastic deformation energy.One part of the elastic deformation energy would be released and transferred into the kinetic energy of the impactor in the form of rebound velocity while the other part would be represented as elastic vibration of the sandwich beam.The time history of strain energy of the sandwich beam could be obtained from numerical simulation results in Ref.[16], as presented in Fig.9.It is seen from this figure that after the impactor separated from the front face of the sandwich beam, the strain energy dropped but remained as constant,with almost no oscillation observed,indicating that the elastic vibration of the sandwich was very small and negligible.Thus, we could assume that the elastic energy stored in the sandwich beam in each impact would be entirely transferred into the rebounding kinetic energy of the impactor.In this paper,the ratio of the absorbed energy to the initial impact energy was defined as‘energy absorption coefficient’,and the square root of the ratio of rebounding energy to the initial impact energy was defined as‘energetic coefficient of restitution’.The‘energetic coefficient of restitution’could be expressed by Eq.(1)[17-18].

Fig.9 Time history curves of strain energy of sandwich beam obtained from numerical simulations[16]
Guo et al[19-20]performed experimental and numerical studies on the dynamic responses of metal foam sandwich plates under repeated impact loadings.It is found that as the impact number increases, the loading stiffness of the metal foam sandwich structures increases, and the elastic strain energy increases,resulting in the increase of the rebounding effect of the sandwich structures,while its increment declines.This phenomenon also occurs on the metal foam sandwich beam under repeated impacts in this paper.The rebound velocity is provided in Tab.1,and the energetic coefficientof restitutionercan be calculated by Eq.(1), then the energy absorption coefficienteican be gained by Eq.(2a).

Tab.1 Dynamic responses of MFSB under repeated impacts
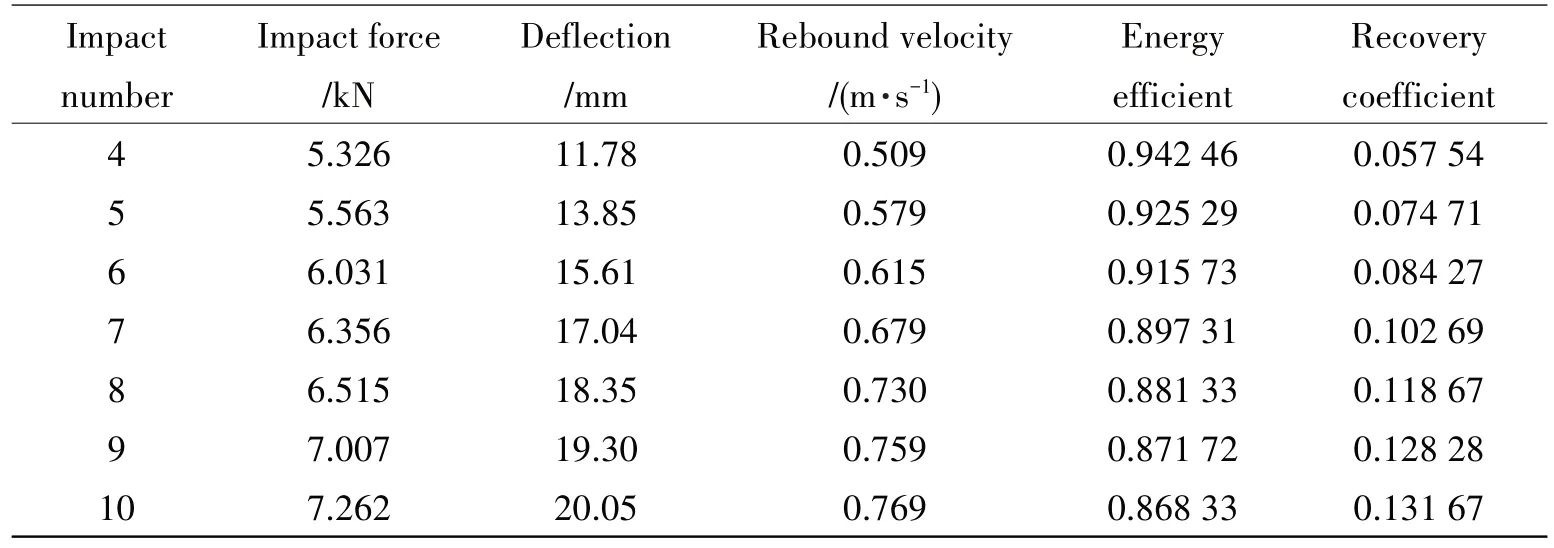
Tab.1 (Continued)
As shown in Fig.10,according to its trend,the curve of the energy absorption coefficient vs.the impact number can be divided into two parts.As the impact number increases, the energy absorption efficient and its increment decrease, but approach constant values.In order to make a more accurate description of the relationship between the energy absorption coefficient and the impact number,fitting formula were derived,as given by Eq.(2b).

Fig.10 Correlation between energy absorption with impact number
2 Theoretical analysis
2.1 Unified yield criterion for sandwich structures
When structures are subjected to intensive external loadings, the plastic deformation will occur,in the form of plastic bending and/or axial stretching.Therefore,both effects of the bending and stretching should be taken into account during the adoption of yield criteria.A sandwich beam consists of two front faces, core material and two rear faces, the stress states are much more complicated than those of a solid beam.According to the principle of force superposition, however, the stress of a sandwich beam can be decomposed into pure bending and uniaxial tension.The deformation profile of the MFSB measured from impact test is plotted in Fig.11.
The thicknesses of face sheet and core aretandc,the width of the beam isb,the distance between the neutral axis and the bottom of rear face ish.The yield stress of face sheet isσf,while the yield stress of metal foam core isσc.Meanwhile,MandNdenote the bending moment and axial force,respectively,andMPandNPare the fully plastic bending moment and fully plastic axial force,respectively.Assumingξ=h/(c+ 2t),and then the stress state of the sandwich structure can be divided into two cases,according to the location of neutral axis,as shown in Fig.12.
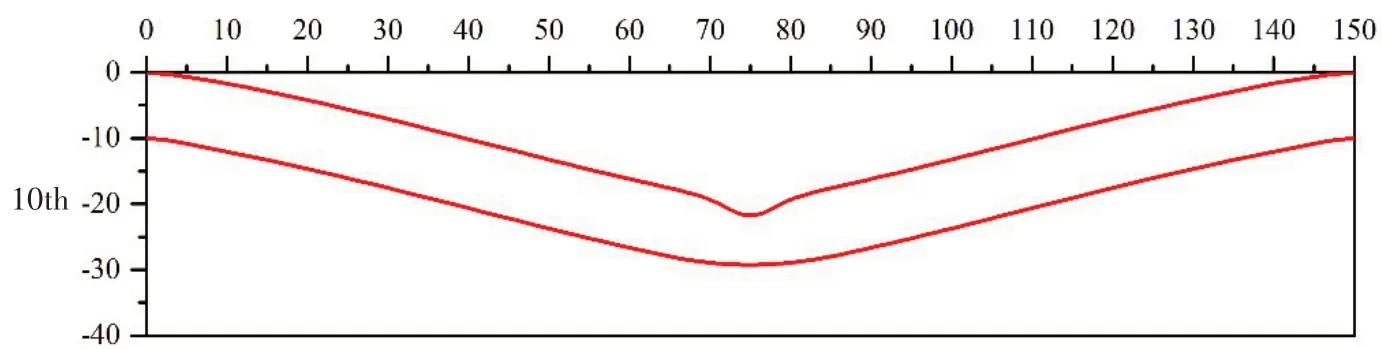
Fig.11 Deformation profile of MFSB measured from impact test
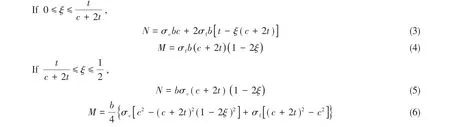
Thus,the plastic yield bending moment and plastic yield axial force can be expressed as following:
To simplify the calculation, the stress and thickness are non-dimensionalized.By definingσˉ=σc/σfandtˉ=t/c,it can be obtained that
From Eqs.(3)-(8),we obtain

Combining Eqs.(12)and(13),yield criteria can be rewritten as

Fig.13 Yield surface of the rectangular sandwich core-section
The yield surface of the rectangular sandwich core-section is shown in Fig.13.
2.2 Bounds of solutions

Therefore,square yield surface of the sandwich core-section can be depicted in Fig.14.

Fig.14 Square yield surface of the sandwich core-section
As for a sandwich beam with fixed ends, if only the plastic bending moment consumes energy,the plastic energy dissipation rate can be expressed as

Similarly,the dimensionless permanent deflection based on the inscribing yield surface can be expressed as
For repeated impacts,the deformation of the previous impact should be taken into account,i.e.the last status of stress and deformation after the previous impact serves as the initial status of the immediate next impact.Based on energy accumulation law,the expressions of dimensionless permanent deflection can be derived as following:
2.3 Validation for the theoretical model
As for a mild steel plate,the yield stress in the theoretical model is assumed to be the approximate value between the initial yield stress and ultimate strength,and expressed as
While for metal foam core,the yield stress is assumed to be the plateau stress,i.e.
In order to verify the validity of the theoretical model proposed above, the material properties and geometric parameters are taken as the same with the impact tests.What's more, the boundary condition,impact mass and impact velocity etc.also remain the same as the impact tests.Hence,in the verifying test of the theoretical model, the impact mass is 7.884 kg, the impact velocity is 2.12 m/s, and the impact energy is 17.8 J.The geometric parameters and material properties as well as dimensionless parameters of the metal foam sandwich beam are summarized in Tab.2.
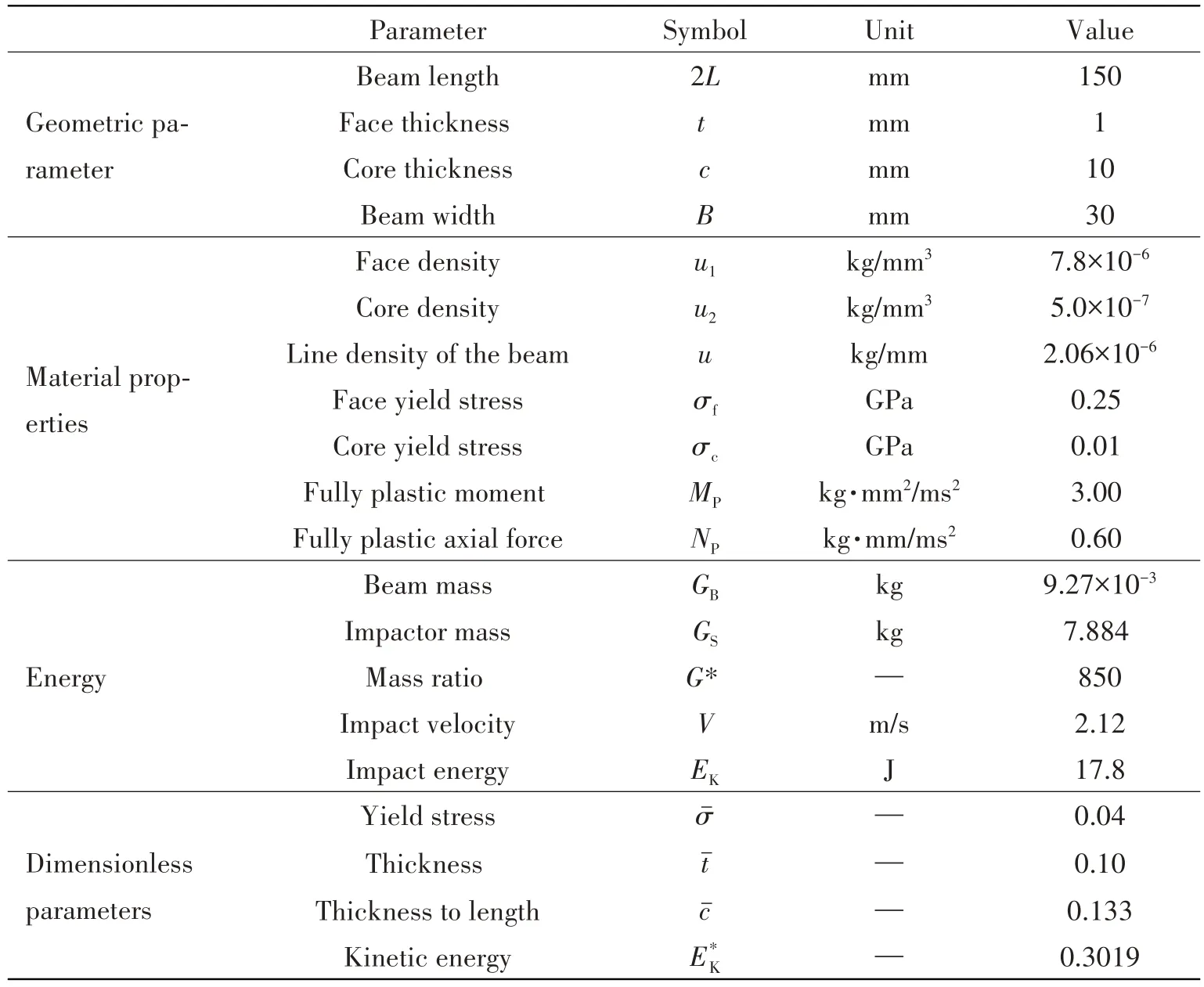
Tab.2 Parameters used in the verifying test of the theoretical model
The dimensionless deflection of the MFSB in different impact numbers obtained from different methods is presented in Tab.3.

Tab.3 Dimensionless deflection of MFSB in different impact numbers
It can be seen from Fig.15 that when the impact number is below 8,the difference of deflection between the theoretical prediction and the real impact test is within 10%.While as the impact number increases,the elastic effect of the sandwich beam is enhanced,thus the difference increases rapidly.For example, when the impact number is 10, the difference would reach 17%, which is relatively large and cannot be accepted.Thus,it can be concluded that when the impact number is larger than a specific value,the elastic effect of the sandwich beam cannot be neglected.
In order to enhance the accuracy of the results,the influence of elastic energy is considered in conjunction with the energy absorption coefficient obtained from impact tests.When considering the effect of rebound,the absorbed energy is calculated approximately as the difference between total energy and the stored elastic energy,then the plastically dissipated energy can be expressed as
The correlation between energy absorption coefficient and impact number can be gained from repeated impact tests,which is illustrated in Eq.(2).

Fig.15 Correlation between dimensionless deflection and impact number
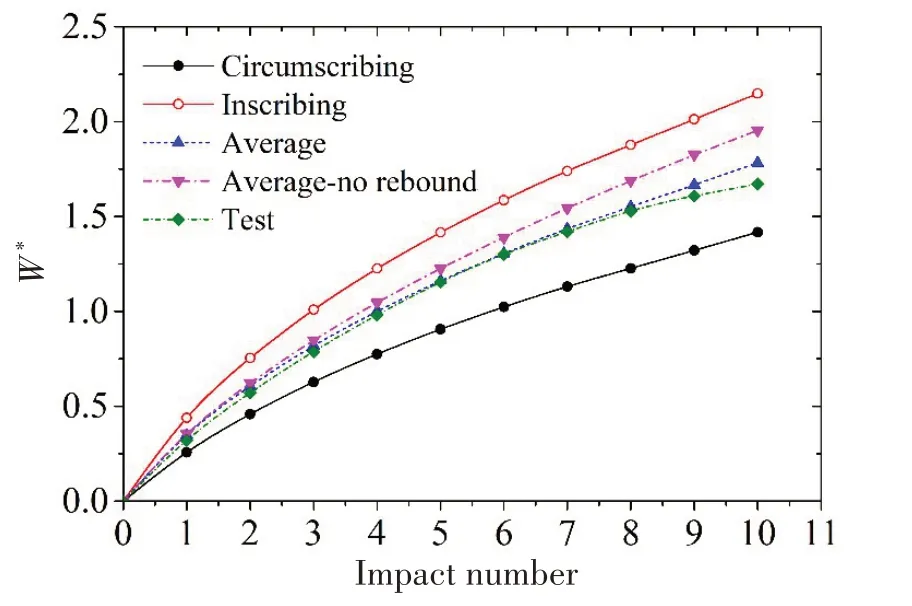
Fig.16 Correlation between dimensionless deflection and impact number considering rebound effect
As depicted in Fig.16, regarding the dimensionless deflections, when considering the rebound effect, the theoretical prediction are very close to the real impact tests.The dimensionless deflections of impact tests lie between the results obtained from the inscribing yield surface and the circumscribing yield surface whilst the average value obtained from these two square yield surfaces almost coincides with the result of impact tests.It can be concluded that, the corrected theoretical model is accurate enough in predicting the permanent deflections of the metal foam sandwich beam suffering from repeated impacts with rigid mass.
However, this theoretical model has made some assumptions, which would be responsible to the differences between the theoretical analysis and the experiments.One factor is the friction,which consumes energy in the impact tests, while the theoretical model does not take it into account.The second factor is the strain hardening, which the material of face sheet would experience during impact tests as the deflection increases, while in the theoretical model, the yield stress of face sheet is taken as the average of initial yield stress and ultimate strength.Thus,when the deflection is small, the yield stress of theoretical model would be larger than real one, but it would be smaller when the deflection is larger.
Based on the aforementioned analysis and comparison, it is confirmed that the prediction of the theoretical model agrees well with those of experiments,verifying that the theoretical model proposed in this paper is sufficiently accurate in analyzing the large dynamic deflections of metal foam sandwich beams under repeated impacts.
To be exact, the proposed theoretical method in this study also has its limitation.The rebound effect of the sandwich beam is obtained from the impact tests, while the elastic energy of the sandwich beam is related to the geometric and material parameters.That is to say, without performing appropriate repeated impact tests, the rebound effect cannot be predicated accurately.Thus, in future studies,in order to improve the accuracy of the theoretical predictions,the elastic energy of the beam can be evaluated by conducting a systematic numerical simulations[21].The equation to predict the rebound effect of the sandwich beam can be empirically derived by a regression analysis of the numerical results,in which the impact energy,geometric and material parameters can be taken into account.
3 Conclusions
The dynamic deformation behavior of a metal foam core sandwich beam suffering from repeated impacts was experimentally and theoretically investigated in this paper.The repeated impact tests of MFSB were conducted by using INSTRON 9350 drop tower,the time history of impact force and velocity were obtained and discussed, and the plastic energy absorption and rebound effect were examined.Then,a complete theoretical model was proposed based on the rigid plastic assumption, in which the rebound effect was considered, while the bounds of solutions were derived.Some conclusions can be drawn as follows:
(1)When suffering from repeated low velocity impacts,the displacement of the sandwich beam is distributed in a linear form from the middle span to the two ends, and the deflection increases with the impact number, while the increment declines.The external impact energy is mainly consumed by plastic hinge rotation and axial elongation.As the impact number increases, the plastic energy dissipation in each impact decreases.By comparison, the rebound energy increases with the impact number, indicating the rebound effect gradually becomes more important during repeated impacts.
(2) The influence of rebound effect can be determined by using the rebound coefficient obtained from impact tests to modify the results of the theoretical analysis.The permanent deflections predicted by the theoretical model agree well with the impact tests,indicating the theoretical model proposed can be used to predict the dynamic response with a good accuracy.Furthermore, to enhance the practical significance of the proposed method,further study should be conducted to evaluate the rebound effect of sandwich beams by numerical simulations in addition to impact tests.
- 船舶力学的其它文章
- Overview of Some Important Factors for Wave Loads and Springing
- Analytical Approximations for Stick-slip Vibration of the Marine Rubber Bearing-shaft System
- Shaping the Structural Frequency Responses with an Improved Partial Eigenstructure Assignment by Minimizing Modal Energy
- An Integrated Design on Next Generation Subsea Production System Based on Multidisciplinary Design Optimization Method
- Expansion Characteristics of Liquid-filled Cell on Hydrodynamic Ram Effect Subject to the Impact of High-speed Projectile
- An Improved Prediction Method for Structural Response Analysis of Offshore Wind Turbines

