Overview of Some Important Factors for Wave Loads and Springing

,-

(1.School of Naval Architecture and Ocean Engineering,Huazhong University of Science and Technology,Wuhan 430074,China;2.China Ship Scientific Research Center,Wuxi 214082,China)

Abstract:With the growth of ship hull sizes and the emergence of new floating structures,the demand for the design values of wave loads in the new codes is becoming increasingly intense.At present,this design is primarily determined by means of numerical prediction, modelling and full-scale ship measurements.In making a numerical prediction, many factors like structural modelling of springing(wave-induced vibration) and hydroelasticity (wave-structural interaction), numerical methods and nonlinear effects should be considered.Key factors were summarized and proposed, and some prospects for future development were proposed.Large differences between numerical calculation results and model tests for high forward speed still remain.Cross-comparisons between results of different numerical calculation programmes and testing data are important for improving the prediction accuracy of numerical programmes in terms of nonlinearity,high-order responses and high speed.

Key words:wave load;springing;structural modelling;hydroelasticity;model test;full-scale measurement

0 Introduction

Wave-induced vibration(springing)has been recognized in wave loading theory and hydroelastic (wave-structural interaction) theory for approximately 40 years.During this period of time, predictive models have evolved from two-dimension to three-dimension, from two-step methods to direct fluid-structure interactions, from frequency to time domains, and from linearity to non-linearity, but deviations remain between the results of numerical predictions and model tests or full-scale ship measurements.These errors originate from theoretical approximations, difficulty of programming numerical codes, high speed approximations, simplification of slamming forces, nonlinear approximation,structural modelling errors,and other factors.

Springing is a phenomenon of hull resonance under continuous excitation by waves.Since hull structures constitute small damping systems, resonance phenomena are sustained for extended time periods.Under low sea conditions large ship hulls are prone to linear wave-induced vibration.Under moderate and severe sea conditions non-linear springing may occur.For traditional ships, if bending stiffness is small, speed high, and nonlinear excitation great, wave-induced vibration may be more serious[1].Experimental research on the wave-induced and slamming vibration responses of large bulk carriers has been carried out[2], and the numerical predictions of springing resulting from four non-linear programmes are less than the results of experimental measurements, which demonstrates that the mechanisms and numerical predictions of springing have not been thoroughly studied yet.

The springing of large ship hulls during sea navigation causes ship structures to suffer frequent fatigue loads.Based on full scale measurement and analysis of the structural stresses of a 300-metre bulk carrier,it is concluded that the contribution of springing to total cumulative fatigue damage reaches 50%, almost equivalent to the contribution due to low frequency wave loads[3].For a large container ship, due to the large open structure of the deck, springing caused by horizontal bending moment and torsional load also contributes considerably to structural fatigue[4].Drummen[5]investigated the effects of nonlinear wave loads and fatigue damage on modern large container ships by springing and whipping, and concluded that springing is the main contributor to the total structural vibration of large-scale ships and that the main source of structural vibration in slender ships is whipping.Container ships have become longer in the past 20 years, and the increase in length means that vertical two-node vibration frequency has decreased and that the importance of the hydroelastic effects of whipping and springing have become more prominent[6].Jensen et al[7]studied wave-induced ship vibration by random waves and found that springing mainly occurred in low sea conditions and near the top wave, with the nonlinear contribution of springing as important as the linear contribution.Large container ships are subject to torsional loads in oblique waves, and it is necessary to conduct coupling studies of torsional mode and horizontal bending mode[8].The load research report[9]indicated that the springing responses of floating structures are closely related to loading conditions, wave conditions and the total vibration of the hull.Different modal vibrations,including vertical wave-induced vibration, transverse wave-induced vibration and torsional waveinduced vibration,are generated by different ship types.

Thus, wave loads and springing exert an obvious influence on the fatigue and structural strength of ship hulls, which are affected by many complex factors, resulting in considerable difficulty in defining the external load in the codes for ship and marine engineering design.With the increase in scale of ship hulls and the emergence of new floating structures, the demand for accurate design values for loads in the new codes is becoming increasingly intense.At present these are mainly determined by means of numerical predictions, model tests and full-scale ship measurements.In numerical predictions many factors must be considered, such as structural modelling of springing and hydroelasticity, numerical methods and nonlinear effects.The paper summarizes and comments on the key factors affecting wave loads and springing, and advances for future development.Since the literatures summarizing wave loads and springing over the last fifty years are copious,only relevant studies from the past 15 years are considered in this study with no intention of undertaking a comprehensive review.

1 Structural modelling influences on springing and hydroelasticity

For hydroelastic structure modelling,1D beam and 3D FEM models are mainly used.A simplified beam model for torsional and horizontal bending vibrations proposed by Malenica et al[10]can be used to evaluate torsion and horizontal bending loads during preliminary design stage for ships.One simplified beam model and a full 3D FEM model for a barge were compared by using this model.An elastic beam model was adopted to simultaneously simulate the vertical, transversal, and torsional stiffnesses of a container ship while considering the torsional moment, horizontal and vertical bending moments of the ship hull[11], as shown in Fig.1.

Hirdaris et al[12]investigated 1D and 3D structural modelling of one bulk carrier in the hydroelastic domain, assessed the forces of each mode, including vertical shear force and bending moment, by using 1D beam and 3D FEM models, and found that the results of the first elastic modes are similar and that the openings on the main deck have some influence on structural stress but almost no effect on the overall external loads of the ship's hull.

Senjanovic et al[13]carried out structural modelling for hydroelastic response assessment for an 11 400 TEU ULCS (ultra large container ship), including 1D advanced beam and 3D FEM models,and concluded that shear effects are relative to transverse bulkheads and engine room structure,which are important to torsional and bending moment.The torsion and horizontal bending moments of the 1D beam model are similar to the 3D FEM model at low frequency,but there are comparative differences between the two models at high frequency,including second-order responses.The thinwalled beam model was properly adopted to consider shear influences in the concept phase for floating structures,and the complex 3D FEM model is better for estimation of hotspot fatigue and analysis of structural strength.

Shin et al[14]investigated different structural models for understanding the overall hydroelastic responses of a 16 000 TEU ultra-large container ship designed by combining the 2D potential method and 3D potential method with 3D Green's function and Rankine source respectively in the 1D beam and 3D FEM structural models, and assessed and compared the numerical hydrodynamic results.It was found that the torsional,horizontal and vertical bending moments of the 1D beam model somewhat diverge from the 3D FEM model,but these differences may partially result from the potential method, in which the beam model is combined with a Rankine source in time domain and the 3D FEM model is combined with Green's function in a frequency domain.

In summary, there are several differences in the hydroelastic responses and wave loads of ship hulls between the 1D beam model and 3D FEM because the deformations of the hulls induced by bending, shearing and torsional deformation of the beam model are not completely coordinate with deformations in the 3D FEM structural model.The differences between the two models are related to the accuracy of the beam model.The vertical and horizontal bending of the hull beam is relatively easy to simulate,while the simulation of shear and torsional deformation is more difficult,thereby requiring complex beam models or multiple beams.Therefore,it is suggested that the 1D beam model might be applied during the schematic design phase, and the 3D FEM model might be adopted during the detailed design phase.

2 Numerical solving method investigation

In terms of numerical methods, Gu et al[15]studied a large ship with severe structural damage due to frequent wave-induced vibration during operation.There are four sets of hull wave-induced vibration numerical predicting programmes including linear, non-linear, second-order, frequency domain, time domain, two-dimensional and three-dimensional components.The numerical results from these programmes are more consistent at low frequencies.With the increase in frequency, numerical predictions of vertical two-node vibration differ greatly and the peak positions of the load responses are also different.From the structural stress spectrum obtained by numerical analysis,the results of each prediction method are considerably greater than those from full-scale measurements.This finding demonstrates the need for improvements in the precision of present numerical prediction codes.Kim & Kim[16]carried out studies of wave-induced vibration by oblique waves at zero speed, adopted the 1D beam model and the 3D BEM method to evaluate the hydrodynamic responses of floating structures, and proposed a hybrid BEM-FEM method to calculate nonlinear whipping in the time domain and springing in the frequency domain.Furthermore,Kim et al[17]studied the linear and nonlinear springing by using the hybrid BEM-FEM method in the time domain.Kim & Kim[18]assessed the springing and slamming responses of a ship by using the full-coupling hydroelastic method and considering structural elastic deformation coupled with a fluid field.

Kashiwagi et al[19]proposed two practical methods for ship hydroelasticity problems under forward speed: the Rankine source method in the frequency domain and three-dimensional Green's function method in the time domain.The references[20-21]present the three-dimensional Green's function method to assess the hydroelastic responses and hydrodynamic coefficients of floating structures, and the numerical results of motions and loads are in good agreement with each other.Kim & Kim[22]performed a benchmark research on a 6750 TEU container ship by using 17 numerical calculation codes.

Rajendran et al[23-24]investigated the vertical bending moment, heave and pitch responses of a large containership by using three methods, including 2D strip theory, 3D hydroelasticity in the time domain,and 3D rigid theory in the time domain.It was concluded that results of vertical bending moments agree with testing data but that the numerical prediction slightly overestimates the vertical motions under severe sea conditions.

In the following paragraphs, the numerical methods will be summarized from the perspectives of frequency domain and time domain.

2.1 Frequency domain numerical prediction method

Yao&Dong[25]studied the hydrodynamic interactions of two ships in waves with forward speed including consideration of steady state flow.The frequency domain method was applied including conditions of steady state flow, and a cross-comparison of motions and wave loads was made between numerical results and experimental results in heading seas.The result considering steady flow exhibits more precise results than that not considering.In addition,Kalske&Manderbacka[26]adopted a three-dimensional potential method in the frequency domain with the assumption of forward speed correction.Nakos[27]extensively employed the three-dimensional Rankine source method incorporating conditions of unsteady flow.Furthermore,some references[28-29]developed a hybrid method considering forward speed in the frequency domain by using Rankine source in the inner field and a translating, pulsating Green's function method in the outer field with singularities distributed on the virtual control surface.On the other side,the translating,pulsating Green's function of Havelock form on horizontal line segment[30-32]was studied using a semi-analytical high-order method.

Due to the fact that a large number of reviews in the literature are given over the past fifty years, only two specific aspects of wave load prediction in the frequency domain are described and summarized as follows,considering wave loads and springing.

2.1.1 Second-order theory

The typical nonlinear procedure in the frequency domain method is a second-order theory based on the perturbation principle and is part of two-dimensional slice theory.The second-order term in this theory considers the nonlinear excitation wave force and the nonlinear changes of the hydrodynamic force during vertical motions.Pinkster[33]proposed a method to calculate the frequency domain, second-order wave exciting force of rigid floating structures in three dimensions, which utilizes the pressure distribution on the wetted surface to assess external wave exciting forces on the ship's hull.The final expression of the second-order wave exciting forces includes five terms: relative wave height contribution, the pressure change induced by fluid velocity square, the interaction of first-order motion and first-order pressure gradient, the first-order force rotation effect and second-order velocity potential contribution, approximated by numerical calculation.It is concluded that the first two terms of the second-order wave exciting forces dominate[33]but that Pinkster's derived second-order force misses the coupling influence term between first-order motions[34].

In the field of 3D frequency domain nonlinear hydroelastic mechanics,Wu et al[35]firstly established a three-dimensional second-order hydroelasticity in the frequency domain to assess the nonlinear hydroelastic responses of a very large floating structure[36].Tian & Wu[37]developed one software for prediction of second-order hydroelastic responses in the frequency domain, and the software was also applied to the nonlinear hydroelastic response predictions of mooring systems and small waterline surface catamarans in irregular waves.

Furthermore,Hu et al[38]evaluated the springing responses of a 500 000 ULOC using the previously-referenced 3D frequency domain nonlinear hydroelastic software,assessed hydrodynamic motions and wave loads in heading seas and oblique seas, respectively, compared the hydroelastic responses of the ship in irregular waves with model test data,and investigated the springing influence on structural fatigue.

Wang[39]adopted the 3D linear and nonlinear frequency domain hydroelasticity methods to perform numerical calculations for a 500 000 ULOC and a 156 800 m3LNG ship,and performed modelling tests,calculated the effects of ship draught,structural damping and hull rigidity on hydroelastic responses and wave loads,and studied the effects of springing on fatigue life.

In general, second-order wave theory in the frequency domain mainly considers the quadratic term of the Bernoulli equation,changes on the wetted surface,the normal direction of wetted surfaces and the second-order velocity potential.At the same time,the theory is mainly divided into pressure integrals in the near and far fields.The pressure integral method for the near field integrates wave pressure on the hull surface directly,while the pressure integral method for the far field is derived from the conservation of momentum and energy.Near-field integration can consider forces and moments in full degrees of freedom, while far-field integration methods can only consider forces and moments in the horizontal direction, but the accuracy of far-field integration is higher than that of near-field integration and the calculations are less difficult.Second-order wave force theory in the far and near fields of the frequency domain has been applied in existing commercial software,such as WADAM (DNV), AQWA (ANSYS), and Hydrostar (BV).The numerical results from these programmes are consistent in the far field, but there are large differences in the near field method.On the other hand, Park et el[40]combined the methods of near field and far field with fluid-structure interaction mechanics to investigate the mean-drift forces of one elastic barge.

2.1.2 Irregular frequencies in hydroelasticity

Numerical analyses of the wave loads and hydroelastic responses of the ship hull affected by irregular frequencies are overestimated.Yang et al[41]added a rigid internal free surface to eliminate irregular frequencies in the 3D hydroelasticity, including the cases of finite and infinite water depth.Consequently, the feasibility of the hydroelastic theory was validated for a large bulk carrier and a barge; meanwhile, the effects of irregular frequencies on hydroelastic responses, diffraction forces, and hydrodynamic coefficients were investigated, as shown in Fig.2.The mesh refinement level of the rigid lid was evaluated.For the cases of finite and infinite water depths, these methods efficiently removed the irregular frequencies.It is concluded that in studies of wave loads and hydroelasticity,the irregular frequencies should be removed,especially for large-scale ships.

Fig.2 Irregular frequency elimination of hydrodynamic coefficients[41]for a large bulk carrier in two-node vertical bending mode

2.2 Time domain numerical prediction method

At present,the 3D linear hydroelastic methods in the frequency domain cannot consider the effects of large-amplitude motions, transient wetted surfaces, and slamming effects on hull motions and overall load responses.3D frequency domain second-order hydroelastic mechanics can consider the contribution of first-order velocity potential and first-order response (including rigid body motion and structural elastic deformation) to second-order hydrodynamic forces on the average wet surface,but is limited to second-order responses.A large number of model tests and full-scale measurements have shown that higher-order hydrodynamic forces, such as the third-order, fourth-order,and fifth-order high-frequency wave forces,can also significantly induce hull elastic vibration,especially when coupled with the two-node vertical bending moment or one-node torsion of the elastic hull structure,in which case there are significant higher-order structural vibration responses in ship hulls[42-43].All of these issues urgently require the development of time domain nonlinear hydroelastic methods and the development of related numerical prediction software.

The time domain method holds an irreplaceable advantage over the frequency domain method in dealing with transient problems, such as slamming and deck waves.A theory of complete nonlinearity in time domain was originally proposed.At each instant change in the wetted surface and its direction, the nonlinearity of the free surface, the quadratic term of the Bernoulli equation, and the nonlinear incident potential were considered.Under the completely nonlinear theory, integral equations must be solved for the transient wetted body and free surfaces of floating structures at each time step,requiring readjustment of the grid,establishment of a system of solving equations at each moment, and a high capacity for computing speed and data storage.Other studies considered fully nonlinear problems[44].Landrini et al[45]adopted the Rankine source method and B-spline function to study the full nonlinear free surface flow problem.With the assumption of a linear free surface and body boundary conditions of the ship hull satisfied on the instantaneous wetted body,Beck&Magee[46]calculated large amplitude motions and forces of the underwater diving ball by using the time domain Green function.Lin et al[47]studied the large amplitude motion of floating bodies such as ellipsoids and Wigley ships.Chapman[48]discussed the nonlinearity of the surface using the Rankine source method.Shao & Faltinsen[49]studied the second-order wave excitation forces of the improved Wigley ship for infinite water depth in the heading wave by using the high-order element method in the time domain.It is concluded that wave forces play a major role, while the contribution of the quadratic term in Bernoulli's equation is minor.

2.2.1 Complex Green’s function method in time domain

Using the 3D‘TDGF’(time domain Green's function), Sengupta et al[50]applied a simplified approach to assess nonlinear motions and wave loads based on the three-dimensional seakeeping theory; meanwhile, the numerical results of vertical bending moments and free motions were evaluated for the S175 container ship and a Wigley ship, respectively.Furthermore, Yang et al[51]introduced the 3D‘TDGF’with forward speed into hydroelasticity in finite water depth, and an approach was derived to improve the calculation accuracy of the‘TDGF’in finite water depth, as shown in Fig.3.The wave loads and hydroelastic responses of a 20 500 DWT bulker carrier have been analysed.

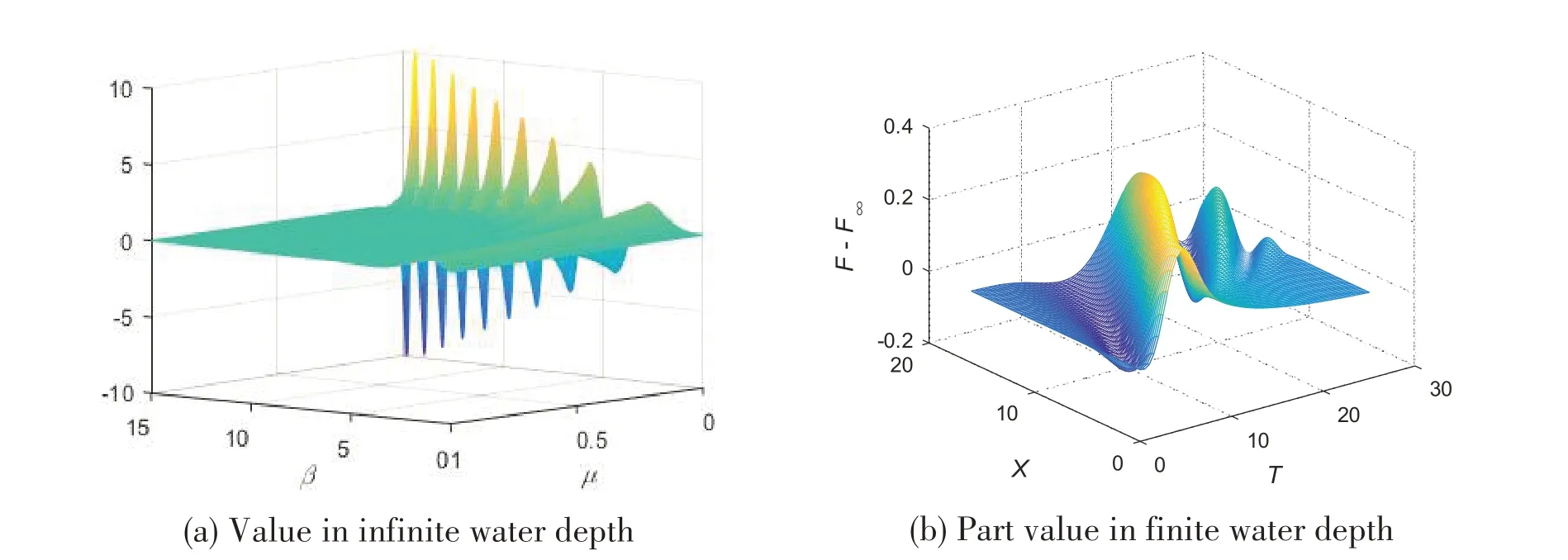
Fig.3 Three-dimensional Green function in time domain[51]

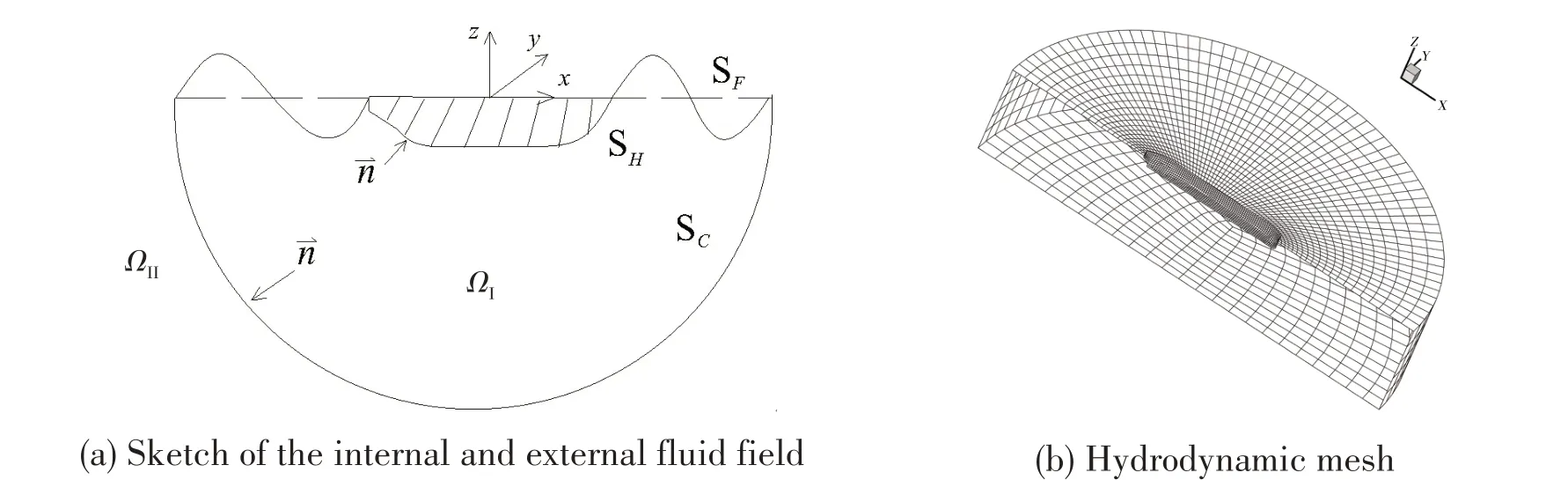
Fig.4 Inner and outer regions matching method[28]

2.2.2 Rankine source

Von Graefe et al[52]compared the wave loads of a 6500 TEU container ship by using the 3D‘TDGF’(time-domain Green's function) method and the 3D Rankine source approach (called GL Rankine).Yang et al[28]introduced the‘IORM’(inner and outer regions matching) method into three-dimensional hydroelasticity.In this method, the Rankine source was applied in the internal fluid field between the ship hull and a virtual control surface, and the‘TDGF’was adopted in the external fluid field outside the virtual control surface,as shown in Fig.4.

Furthermore, compared with the frequency domain method with forward speed cor rection, the GL Rankine method in the time domain yields more valuable results, especially at high Froude number.Kim et al[53]made a comparison of wave loads by numerical results and model testing data for an 18 000 TEU container ship.Chen & Liang[54]also introduced a virtual control surface surrounding the floating body into the multi-domain method.The linear boundary condition for the free surface was satisfied using a‘TDGF’out of the virtual control surface, and the nonlinear factors and viscous effect were applied in the inner fluid field.Furthermore, Chen & Zhu[54]combined a 3D time domain Rankine source method with a high-order boundary element method to assess motion and hydrodynamic coefficients of multi-vessel interactions,and numerical results suggested that steady flow has a strong influence on the motion.

For describing complex nonlinear sea states, a very effective and rapidly convergent HOS(high-order spectral) method has been proposed for long-time simulation using fast Fourier transforms and spectral methods.Xiao et al[55～56]established a time domain method for nonlinear irregular waves and extreme waves based on weakly nonlinear assumptions and the HOS method, and evaluated the motions of floating structures with forward speed.

2.2.3 CFD in fluid-structure interaction

Computational fluid dynamics (CFD) methods aim to calculate the hydroelastic responses of large ships.Paik et al[57]utilized CFD to assess strong nonlinear motions and wave loads by considering viscous effects.Recently, Finnegan & Goggins[58]investigated the water particle velocity and forces of wave energy converters by using ANSYS CFX commercial CFD software, and a numerical approach combining a viscous flow solver, and Robert et al[59]investigated the hydroelastic responses of a flexible barge in the time domain by use of beam model.In addition,Lakshmynarayanana et al[60]investigated the fluid-structure interactions of flexible floating bodies in waves by combining STAR-CCM+ (commercial CFD software) with Abaqus (commercial FEM software).Craig et al[61]studied the fluid-structural responses of a joint high-speed sealift model travelling in a large seaway in the time domain by utilizing OpenFOAM (open source software) and a high-order boundary element method.Moctar et al[62]proposed a computational method that couples nonlinear motion equations with Reynolds-averaged Navier-Stokes(RANS)equations to assess structural vibration.

Generally,the study on wave load and hydroelasticity has focused primarily on nonlinear problems,high speed and numerical stability.

3 Model tests and full-scale measurements

3.1 Model tests in basins

To simulate the profile characteristics of large openings in model tests,container ships are taken as an example,and the vertical,horizontal,torsional stiffnesses and shear centre of the backbone are satisfied simultaneously by model design in a see-keeping basin[63-64], as shown in Fig.5.Furthermore, Lin et al[65]evaluated asymmetric slamming effects on wave loads by using a 1:64 multisegment model test that adopts the U-shape beam to simultaneously meet the structural vibration similarity of torsional,horizontal and vertical stiffness.

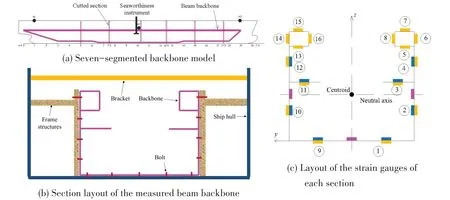
Fig.5 Experimental model in the wave basin(1:77)[64]

A wave load model test performed on a very large ore carrier showed that ballast conditions are more likely to cause springing of the ship structure than full load conditions[39].Multi-segment model test data of the wave load of a 13 000 TEU container ship showed that the wave loads induced by high-frequency vibration are more susceptible to heading direction than low-frequency results[66].The proportion of the high-frequency component to total wave load decreases from oblique seas to beam seas and the peak proportion of high-frequency whipping induced load is 58.73%.

Jiao et al[67]evaluated the motions and wave load of one naval vessel in long-crest waves using numerical prediction and model tests, and carried out full-scale measurements for nonlinear wave loads in short-crest waves.Furthermore,Yang et al[68]investigated the uncertainties of numerical results and model tests for different vessels and wave loads.

In summary, model tests can be used to study wave loads and wave induced vibration for ships under given sea conditions, but may yields some errors due to the scale effect, the approximate mass distribution and the simplification of the steel beam models.It is difficult to simulate torsion,horizontal shear, vertical shear, horizontal bending and vertical bending simultaneously.In addition,there are some limitations to the study of wave-induced vibration using a sectional model test.It is necessary to cut the hull beam into more sections to accurately simulate higher-order elastic vibrations and hydroelastic responses.

3.2 Full-scale measurements in realistic seas

Lin[69]conducted a full-scale measurement on a Bohai‘Changqing’tanker with a length of 221.3 m.A spectral analysis of the deck stresses was performed, finding that the ship does indeed have springing under sea conditions of 7th to 9th wind.Total longitudinal bending stresses of the hull increase by 13% to 17% when considering springing.A full-scale survey of a large ore carrier between St.Lawrence Bay and Rotterdam[3]showed that since no bottom slamming was recorded during the full-scale measurement, vibration stress mainly came from the springing load, and the structural wave-induced vibration damping coefficient obtained by measurement was approximately 0.5%.The time history curve under ballast conditions clearly indicated that the magnitude of springing and wave-induced hull stresses were similar.The stress measurements in the case of a full load showed that structural stress levels from wave-induced vibration are not as high as previously estimated because the wave pressures at the bottom decrease exponentially with an increase in draught.Under a full load,the ship mainly encounters following sea conditions.

Moe et al[70]carried out a full-scale measurement on an ore carrier with a perpendicular length of 281 m.The test time was approximately four months on a Pacific route between the United States,China and Japan.When the significant wave height reaches 3 m or more,vibration damage from the lowest bending mode accounts for nearly half of total fatigue damage.Such full-scale measurements were conducted on a typical Capesize bulk carrier[71]from November 2003 to May 2005.This ship's measurement results were compared with the data[70], showing that 56% of the total damage is caused by springing.

Okada et al[72]performed a three-year onboard survey of a 6700 TEU container ship between 1998 and 2001.According to the analysis of the measured data, the cumulative fatigue damage ratios with and without springing are 0.105 and 0.050, respectively, showing that springing doubles the cumulative fatigue damage.

In summary, a full ship test is necessary because the scale effect can be avoided in a full ship test and the data obtained can more accurately reflect the external load and wave-induced vibration of a ship hull in actual service.However,high cost and the need for multi-party cooperation make it difficult to carry out large-scaled ship tests.Thus,data from ship tests are precious.

4 Nonlinear hydroelasticity and springing

Under the assumptions of potential flow theory, nonlinear wave-structure interactions in floating structures mainly come from the following four aspects:(1)the velocity squared term in the pressure expression of Bernoulli equation for fluids; (2) large motions with an instantaneous wetted surface and the changes of the normal direction of the wetted surface; (3) non-linear conditions of the free surface;and (4) bottom slamming,flare slamming,and green water caused by water coming out of the bottom of the hull.The report of the ISSC Load Committee[73]considered that after decades of development,current thought has covered linear theory to nonlinear theory,2D theory to 3D theory,frequency domain theory to time domain theory, rigid seakeeping theory and hydroelasticity.The current status of numerical predicting methods of nonlinear hydroelasticity and springing is summarized as follows: at present, 2D linear and 3D linear hydroelasticity methods are relatively mature and widely used, but 3D nonlinear hydroelastic methods considering nonlinear hydrodynamic factors or structural nonlinear elastic deformation are not yet mature.It is necessary to consider the influence of non-linear factors in future hydroelasticity research.Furthermore, some references[74-75]reviewed recent advances and future trends in hydroelasticity and ship loads.The time domain method is more advantageous than the frequency domain method when solving nonlinear three-dimensional hydroelastic problems.Wu & Cui[76]summarized the development of 3D linear and nonlinear hydroelasticity and experimental techniques.Temarel & Hirdaris[77]summarized the theoretical development and application of hydroelasticity in the design of ships and marine structures at the 5th International Hydroelasticity Conference.In addition,the ISSC Load Committee has summarized current research progress and methods for considering hydroelasticity[78].In 2009,2012,2015,and 2018, the 5th to 8th International Conferences on Hydroelasticity[77-78]were held in the UK, Japan,Croatia,and South Korea,respectively.

Hirdaris et al[79]studied the nonlinear effects on the wave loads of a 10 000 TEU container ship by comparison of four numerical predicting codes with model test data.The distinctions between numerical results and measured data of the vertical bending moments are relative to heading direction and section position.Furthermore, a nonlinear time domain potential theory has been adopted to evaluate wave loading and hydrodynamic motion[80], in which the predicted results of added damping and added masses of the radiation potential have been compared with model tests and RANSEbased simulations, as well as linear frequency domain results for three different ship types at various forward speeds.The numerical comparison results of added damping are consistent at zero speed, while the added masses show good agreement with forward speed.In addition, Yang et al[81]presented two methods by using the 3D complex‘TDGF’and Rankine source respectively to evaluate hydroelastic responses and wave loads of the ships with forward speed.

Fig.6 Vertical bending moment of linear responses at midship[22](head sea,zero speed)

The responses of vertical bending moment,pitch and heave were predicted to assess the influence of forward speed at Froude numbers of 0.05 and 0.12.The statistical values of linear responses were calculated, and the comparisons were performed between model test data and numerically predicted results[22], as shown in Fig.6.The statistical average of numerical results agrees with the model test data for the linear vertical bending moment without forward speed.At the same time,the nonlinear results for vertical bending moment in the time domain are shown in Fig.7.The apparent high-frequency vibrations are due to springing and whipping.It is concluded that the predicted results exhibit a greater error at high speeds, and it is difficult to obtain satisfactory numerical results.The discrete characteristics of the numerical prediction results indicate a need for improvements in direction and thinking in future research.

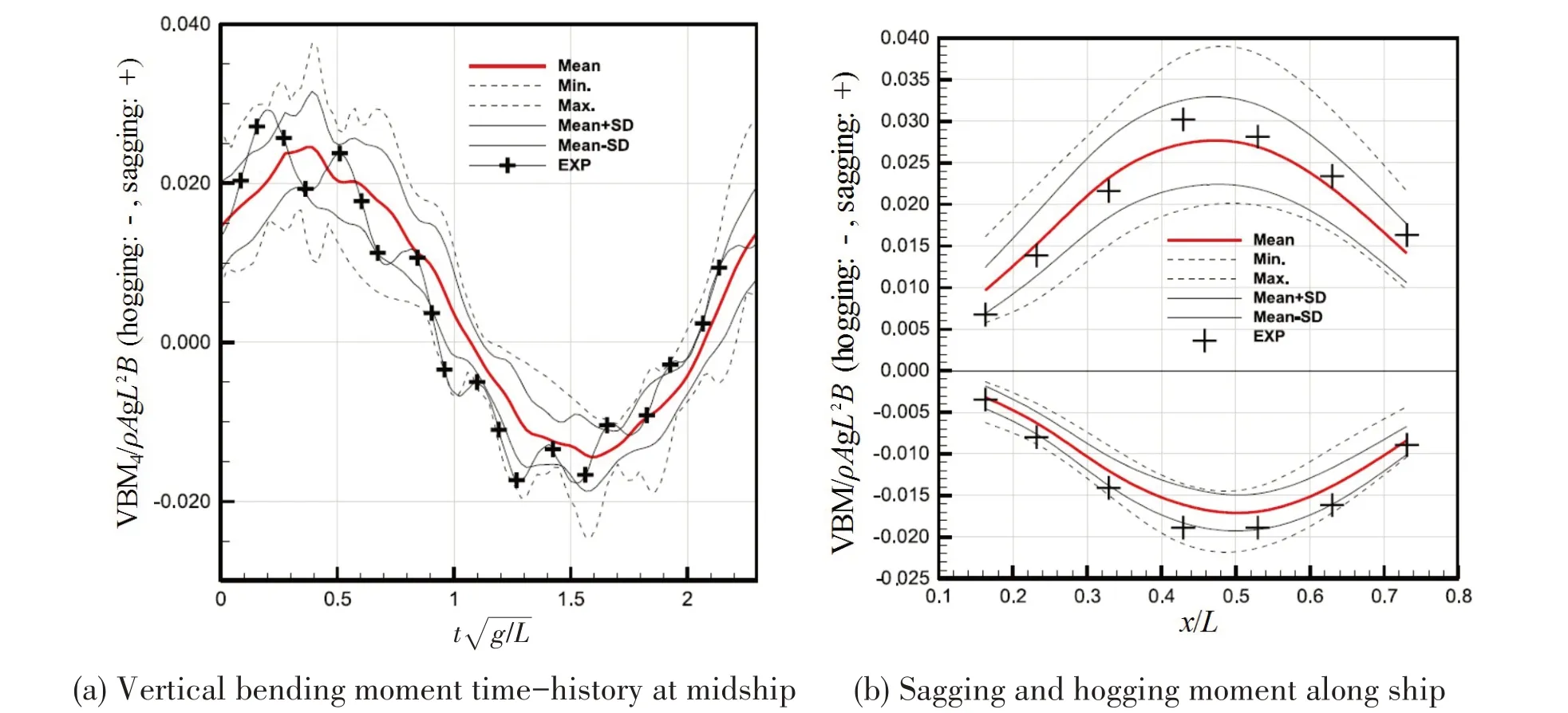
Fig.7 Vertical bending moment[22](Fr=0.05,λ/L=1.07,Wave height=10.9 m)

In recent years nonlinear 3D hydroelastic mechanics have been fully investigated by considering various nonlinear factors including slamming pressure,nonlinear hydrostatic restoring force and incident wave exciting force.The 3D Rankine source is combined with a Wagner model in the time domain[42].A nonlinear 3D hydroelastic method has been developed in the time domain by considering slamming pressure and nonlinear hydrostatic restoring force[66,82].The nonlinear wave loads of a 205 000 DWT bulk carrier have been evaluated by comparing the numerical results from the Rankine source method and model test data,including the springing and whipping effects[28].

An indirect 3D hydroelastic method in the time domain containing an impulse response function and considering nonlinear incident wave exciting force has been adopted to assess wave loads induced by slamming pressure on a naval vessel in irregular seas[67].Compared with model test results, the peak value of the pitch is overestimated by numerical predictive codes.This overestimation is observed because nonlinear diffraction and radiation exciting force are not considered in the numerical prediction programme.Moreover, the asymmetric characteristics of sagging and hogging bending moment are more distinct in the model test data than in the numerical results,especially in the bow position while the numerical codes have underestimated the sagging bending moments of bow positions.

The nonlinear horizontal and vertical bending moments of a 13 000 TEU container ship were numerically assessed using the Rankine source method and numerical damping beach in the time domain[83]and compared with model test data.Nonlinear factors include slamming pressure, nonlinear hydrostatic restoring force and incident wave exciting force.It is concluded that the nonlinear hydrostatic restoring force is dominant in the cases of oblique and beam seas.The wave loading component induced by high-frequency structural vibration is sensitive to wave direction.Moreover,the high-frequency responses of the wave loads must be considered in the cases of heading and heading oblique seas,where the slamming effect could not be ignored.

The wave loads and motions of a 6750 TEU container ship have been studied using a 3D nonlinear hydroelastic method in the time domain[84], including two methods, the complex 3D‘TDGF’and the Rankine source.The nonlinear response of the vertical bending moment and hydrodynamic motions at the midship section are evaluated considering slamming pressure, nonlinear hydrostatic restoring force and incident wave exciting force,including springing and whipping effects.Some important conclusions are reached: (1) there is little effect on heave and pitch induced by the nonlinear incident wave exciting force (mainly causing high-order responses in VBM)and slamming pressure(only inducing two-node vertical bending vibration),but there is a large effect on vertical bending moment; and (2) the nonlinear hydrostatic restoring force induces larger motions and vertical bending moments with few high-order responses.The nonlinear results of heave are smaller than the linear result,but the physical laws of pitch are opposite.

In general,the nonlinear effects of marine structures mainly cover changes in the wet surface of the hull, non-linearity of the free surface, higher-order wave forces, slamming effects, and waves on the deck causing the hydrostatic restoring force of the hull and incident waves force, diffraction wave force and radiation wave force to appear nonlinear.In medium- and high-sea conditions, the nonlinear effects of ship motion, especially wave loads, cannot be ignored.On the other hand, nonlinear wave forces from different frequency effects must be considered in evaluating hydroelasticity.At the same time,with the development of large-scale marine structures,the effect of high-frequency nonlinear wave forces on the hydroelastic responses of structures is becoming increasingly significant.These realistic demands in the assessments of ship motions and external wave loads make the development of three-dimensional nonlinear theory and nonlinear hydroelasticity considering forward speed very urgent.In particular, greater attention must be focused on high-order springing at high speeds.

5 Summary and prospects

There are many studies of vertical wave-induced vibration employing diverse numerical calculations and model tests.Some studies of horizontal wave-induced vibration have also been conducted,but there are few studies on torsional wave-induced vibration,primarily limited by the difficulty in model test simulations.In addition, although a variety of two-dimensional and three-dimensional numerical calculation methods can accurately evaluate wave-induced vibration responses and wave loads in zero-speed and low-speed conditions,there remain large discrete errors between numerical calculation results and model tests for high forward speeds.Furthermore,future studies concerning the wave loads and springing responses of ships are important for the following purposes:

(1) For high speed conditions, to improve the numerical prediction of hydroelastic responses and to improve forecast accuracy and efficiency;

(2) For model tests, to establish a benchmark test database based on full-scale measurement and verification for multiple ship types;

(3) To perform uncertainty analysis of structural modelling for different types of floating structures and modelling approaches;

(4)To conduct further research on large-open hulls,such as a container ship,especially model tests and full-scale ship measurements.

Although some progresses have been made in the study of nonlinear hydroelasticity,further research is needed on 3D nonlinear hydroelastic responses and wave loads as follows:

(1) To improve nonlinear hydroelasticity predicting programmes for accurate prediction of the responses of wave-induced vibration at high orders;

(2) To consider high speed influence properly and improve the accuracy of numerical programme prediction under high-speed conditions;

(3) To perform full-scale measurements and model tests of various very large following a standard procedure, and improve the prediction accuracy of numerical programmes in terms of nonlinearity, high-order responses, and high speeds through cross-comparisons among different numerical calculation programmes and testing data;

(4)To improve the present methods for calculating slamming pressure and whipping responses to contribute to a more accurate numerical predicting programme;

(5) To improve the calculation efficiency and stability of hydroelastic software in the time domain.