Analytical Approximations for Stick-slip Vibration of the Marine Rubber Bearing-shaft System
,-,,,-
(1a.College of Underwater Acoustic Engineering;b.National Key Laboratory of Underwater Acoustic Technology,Harbin Engineering University,Harbin 150001,China;2.Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University),Ministry of Industry and Information Technology,Harbin 150001,China)
Abstract:The one-degree-of-freedom mass-spring-belt model is established for describing frictioninduced stick-slip self-excited vibration by considering the stribeck-effect friction model and the normal load.The approximately analytical expressions for stick-slip oscillation amplitude are derived by using Krylov-Bogoliubbov-Mitropolsky method.Both the stable and the unstable steady-state solutions can be obtained by the analytical expressions.In addition,results from the analytical expressions agree well with results from numerical integration of the nonlinear governing equations of the model.Subsequently, the influences of kinetic friction coefficient and normal force on self-excited vibration amplitudes are discussed.The novelty of this work is the derived approximately analytical expressions for stick-slip oscillation amplitude, by which the stable and the unstable steady-state solution can be obtained.
Key words:friction;self-excited oscillation;analytical approximation;stribeck effect;stick-slip
0 Introduction
Many kinds of mechanical systems,such as fluttering machine tools[1],chattering shaft-bearing systems[2-3]and grating brakes[4], have the phenomenon of the friction-induced self-excited vibrations, which have been the significantly important cause of the instabilities and vibrations of systems.Under the condition of low speed and heavy load,the water-lubricated rubber stern bearing of a ship is often in a mixed or boundary lubrication condition.The stick-slip self-excited vibration probably occurs,which will aggravate the vibration and further destroy the acoustic stealth of ships.In the stick phase, the bearing lining is relatively stationary with the shaft.The elastic deformation of bearing lining increases and its energy accumulates gradually.The stick phase ends when the elastic force is greater than the static friction force between the shaft and the lining.The lining and the shaft separate under the action of elastic force, and enter the slip phase.At this time, the adhesive point will bounce back in the opposite direction and gradually form a new adhesive motion.The stick and slip phases appear alternately to result in the stick-slip self-excited vibration of the water lubricated rubber bearing-shaft system.The time domain and phase diagram of stick-slip vibration[5]are shown in Fig.1.

Fig.1 Diagram of stick-slip vibration
Lots of numerical works have been performed to investigate the self-excited vibrations.Panovko and Gubanova[6]found that the self-excited oscillations happen only when the belt velocity is lower than a special value.Popp[7]presented models and numerical and experimental results for four systems that are similar to the mass-on-moving-belt.Sinou and Jezequel[8]studied the role of damping in mode-coupling instability and the amplitude of limit cycle of a simple nonlinear two degrees-of-freedom model which had cubic nonlinear contact stiffness in order to avoid bad design.Leine[9]numerically simulated stick-slip vibrations using several different friction models such as the smoothing and switching methods.Feeny[10]summarized a very readable historical review on dry friction and stick-slip phenomena.
However, only a few of researchers can provide analytical expressions for friction-induced self-excited vibration amplitudes.Nayfeh[11]and Tondl[12]described self-excited oscillations of the mass-on-belt system, presenting approximate expressions for the vibration amplitudes for the case,where there is no sticking between mass and belt.Thomsen[13-14]set up approximate expressions for stick-slip oscillations of a friction slider,which are accurate only for very small differences in static and kinetic friction.Hoffmann and Bieser[15]determined the finite-amplitude limit cycles of two-degree-of-freedom model by the technique of Harmonic Balance and KBM, but only considered the linear contact stiffness instead of non-linear contact stiffness which is actually contained in most real systems.Kruse[16]proposed a new treatment for predicting the self-excited vibrations of nonlinear systems with frictional interfaces,called the constrained harmonic balance method.
Furthermore, most of the present studies on the analytical expressions for friction-induced self-excited vibration amplitudes employ the coulomb-type friction law, which cannot accurately describe the friction force occurring in the reality.The coulomb friction model includes a static friction part and a kinetic friction part,the kinetic friction coefficient is constant,and the model is generally used in the dry friction state.The stribeck friction model also includes the static friction part and the kinetic friction part.The kinetic friction coefficient varies with the velocity,which is generally used for boundary lubrication, mixed lubrication and hydrodynamic lubrication.Obviously,stribeck friction model is able to describe the lubrication state of bearing-rotating shaft system more accurately.The models of coulomb friction and stribeck friction are shown in Fig.4.This paper,considering the friction force model with the stribeck effect,provides the approximately analytical expressions for stick-slip vibration amplitude in friction self-excited model using KBM.Both of the stable and unstable steady-state solutions can be obtained by the analytical expressions.
1 Model
For the sake of deriving the approximately analytical expressions for stick-slip vibration amplitudes of friction-induced stick-slip self-excited models considering the friction model with stribeck effect, a one-degree-of-freedom friction self-excited model with stribeck effect and normal load is presented in this paper.The simplified process is as follows.To the water lubricated rubber bearing-shaft system, the stick-slip self-excited vibration mainly occurs in the torsional direction.This paper therefore focuses on the torsional direction.The transverse section of the rubber bearing-shaft system is shown in Fig.2(a), which includes the rotation of the shaft and the torsional vibration of the bearing lining.To facilitate the study, the rotation of the shaft can be equivalent to the rotation of the belt,and the torsional vibration of the bearing lining can be equivalent to the motion of the mass along the belt.Among them,the spring stiffness is the torsional stiffness of the bearing lining.The simplified results are shown in Fig.2(b).

Fig.2 Simplified process from the bearing-shaft system to 1-DOF simplified stick-slip model
Fig.2(b)depicts the model in detail:a rigid mass block slides over a belt that moves at constant speedVd, which is supported by the horizontal linear springkand dampingc, and the normal forceFNis regarded as the pre-compression force applied on the mass block, which is equal to the normal contact forces at the interface between the sliding mass and the belt.Thexaxis of the coordinate system represents the horizontal motion displacement.

Fig.3 Schematic picture of testing bench for the friction coefficient of water lubricated bearing

Tab.1 Parameters of the tested shaft and bearing
The friction coefficient in this paper comes from the experimental test.The testing bench for the friction coefficient of water-lubricated bearing is seen in Fig.3.After multiple measurements and average treatment, the friction coefficient of the waterlubricated rubber bearing is obtained and shown in Fig.4.The main parameters of the water-lubricated rubber bearing are seen in Tab.1.Eq.(3) describes the typical stribeck friction model, and the coefficients in the friction model are obtained by fitting the testing curve of friction coefficient.
The nonlinear dynamic equation of the model is
wherem,candkare respectively the mass,the damping and the stiffness of the model.The oscillation displacement is described by the variablex.TheFfandFNseparately denote the tangential contact force at the interface between the sliding mass and the belt, and the normal force.The tangential contact forceFfis the product of the normal contact force and the friction force coefficient with the negative damping effect that is also called stribeck effect.It is the function of the sign function,the relative sliding velocityvr, kinetic friction coefficientμ0, static friction coefficientμ1, coefficientβcontrolling the gradient ofμwith respect tovr.
With the purpose of determining the static equilibrium position,the first-order and second-order differential forms ofxdisplacement are set to be zero.Substitution of Eq.(4)into Eq.(1),the static equilibrium positionxeare obtained as Eq.(5), which is determined by normal contact force,spring stiffness,friction coefficients and driving speed of the belt.

Fig.4 Models of coulomb friction and stribeck friction
In order to study motions near this static equilibrium point, the new coordinate spaceuis set up by shift the original point to the static equilibrium point through the following equation.In the new coordinate space,Eq.(1)can be rewritten as Eq.(7).

2 Solutions
The KBM method is used to solve the nonlinear differential governing equations of the model in this chapter.After some terms of Eq.(10) are transferred from the left-hand side to right-hand side,Eq.(10)can be rewritten as

It should be noted that comparison of the varying level ofψwith respect to timet, the varying level of amplitude and phase versus timetis slight.The averaged amplitude and phase therefore can be obtained by averaging the amplitudes and phases over one period of the fast timescale,which means
2.1 Solution of derivative of the amplitude and the phase

In Eq.(22), the upper and lower limit of the integration, and the corresponding value of the sign function are determined by the law as shown in Fig.5.
The integration of the polynomials in Eq.(22)can be calculated to be the following equations:

Fig.5 Law of determining the value of the sign function
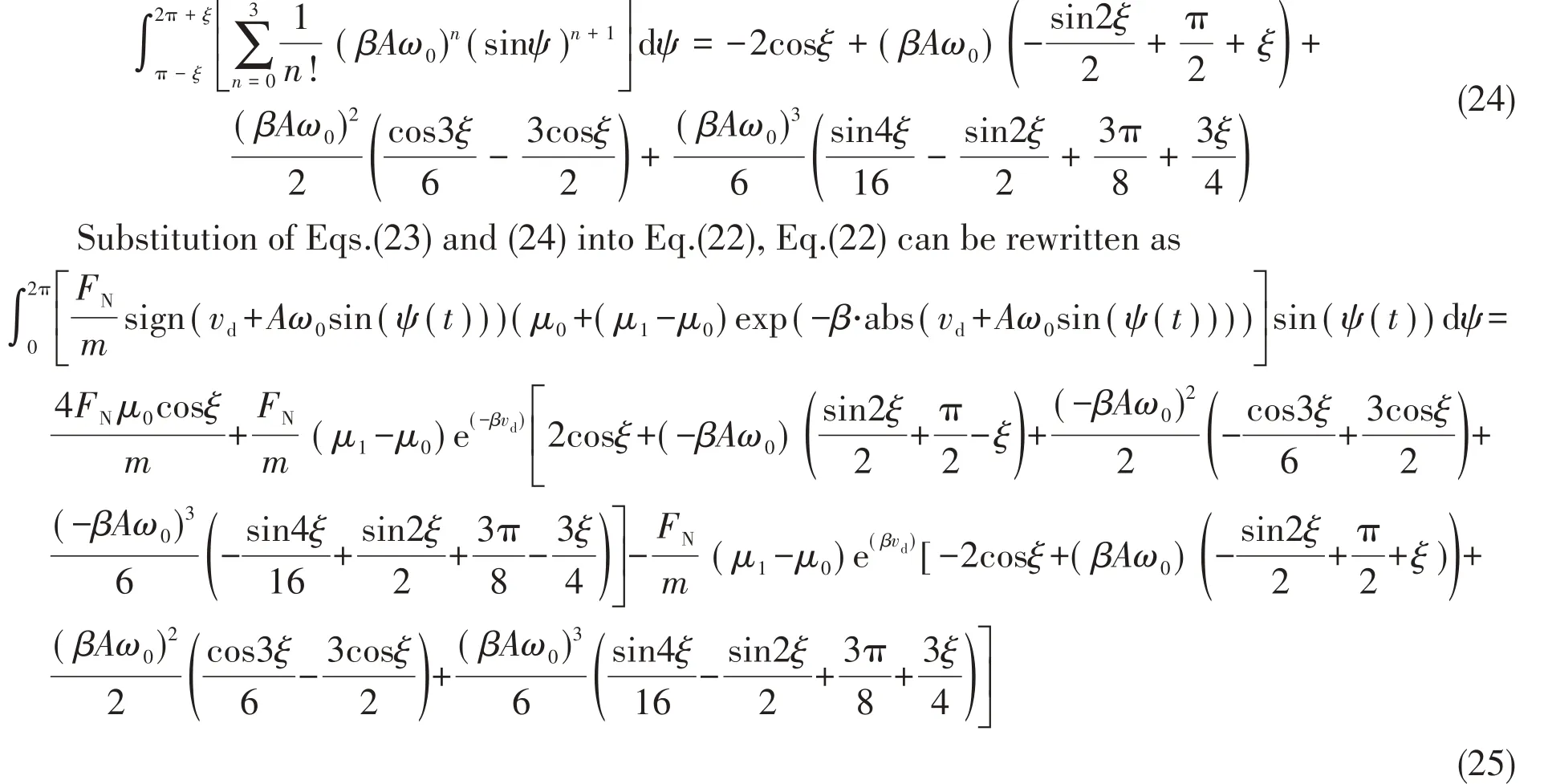
So far, the expression of the first integration terms has been solved by Eq.(25).Similarly, the expressions of the second and third integration terms can also be solved, which are as the following equations:

Eq.(19)can be rewritten as
2.2 Solutions of the amplitude and the phase
Eq.(28) and (29) respectively describe the derivative of the amplitude and phase with respect to time.When the harmonic oscillations of the model reach the steady state, the amplitudes and phases will be constant, the derivatives of which are equal to zero.The following equations are therefore obtained:
There is only one unknown variableAin the nonlinear algebraic Eq.(31), as can be solved using the Newton-Raphson iterations.The phase is determined by the initial condition observed from Eq.(30).Up to now,we have obtained the solutions of the amplitude and the phase by the above derivations.
3 Numerical validation and parameter analysis
The approximate analytical expressions for stick-slip vibration amplitude in friction self-excited model are derived as Eqs.(30)-(31) by using KBM method.In order to check the validity of the approximate analytical expressions, the comparisons of stick-slip self-excited vibration amplitudes between approximate analytical expressions and numerical integration are carried out.Subsequently,parameter discussion about the influences of kinetic friction coefficient and normal force on selfexcited vibration amplitudes are performed.
In this chapter, we therefore define the following parameter values of the practical ship shafting system,except otherwise specified.As the research model in this paper focuses on the water-lubricated rubber bearing lining, relevant parameters of the rubber lining are mainly given, as shown in Tab.2.

Tab.2 Parameters of the stick-slip self-excited vibration model
3.1 Numerical validation
Fig.6 depicts the comparison of the horizontal oscillation amplitudes between approximately analytical prediction and numerical integration, and also describes the dynamic bifurcation of the oscillation amplitudes versus the belt speed.The black lines denote the results from the numerical integration,of which the solid line represents the stable numerical solutions and the dash line represents the unstable numerical solutions solved by the means of integrating in reverse time for unstable limit cycles[17].The red rounds denote the results from analytical prediction derived by KBM method.

Fig.6 Dynamic bifurcation diagram of the vibration amplitude with respect to the belt speed
As observed from Fig.6, the unstable equilibrium branche1and the stable periodic branchp1arise from the origin in the meanwhile.The equilibrium branches consist of equilibrium points which represent the static equilibrium state of the mass,and the periodic branch consists of limit cycles which represent horizontal vibration with stick-slip or pure-slip.The stable equilibrium branche2and the unstable periodic branchp2are connected to the unstable equilibrium branche1at the point which is called subcritical Hopf bifurcation point.From the bifurcation point,the unstable periodic branchp2arises, and then converges with the stable periodic branchp1into the point,which represents the fold bifurcation point.
Obviously,the analytical expressions derived by KBM can give the stable and unstable periodic solutions,denoted by the red rounds.The agreement of the stable periodic results from the analytical expressions and the numerical integration is quite good.Moreover, to the prediction of the unstable periodic solution, the analytical expressions also acquire the solutions with a not bad precision, which has never been obtained by the analytical methods in any public literatures up to now.The errors mainly come from the conflict between the harmonic assumption of KBM and the fact that the horizontal oscillations are not actually strict harmonic behaviors.
3.2 Parameter analysis
The effects of a series of system parameters on the horizontal oscillation amplitudes are illustrated in Fig.7 and Fig.8.It is seen from Fig.7 that the amplitudes of the friction-induced self-excited oscillations slowly increase, with the increasing of the normal force, implying that low level of the normal force can lead to the small amplitudes of the oscillations or even static equilibrium,which is helpful to control the friction-induced vibration.In addition,when the normal force gradually increases, the errors between stable numerical and KBM solutions slowly become greater,which results from the prolonged stick phase of the stick-slip oscillations and the gradual deviation of the oscillation behavior from the strict harmonic.
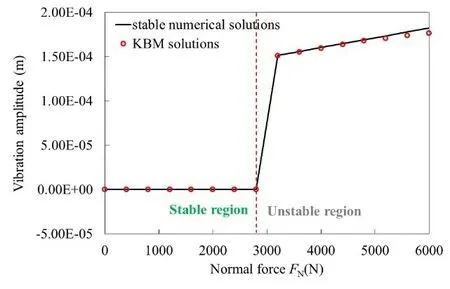
Fig.7 Influence of the normal force on the horizontal self-excited oscillation amplitudes
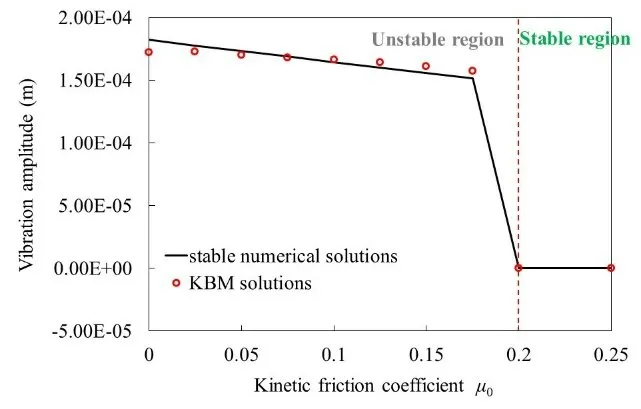
Fig.8 Influence of the kinetic friction coefficient on the horizontal self-excited oscillation amplitudes
Fig.8 shows the dynamic state of the model steps into static equilibrium from the self-excited oscillation while the kinetic friction coefficient isμ0>0.2,which demonstrates that the small distinction of the kinetic and static friction coefficient does benefit the stability of the model.
4 Concluding remarks
One DOF mass-spring-belt model for describing the friction-induced stick-slip self-excited vibration is established by considering the stribeck-effect friction model and the normal load.The approximate analytical expressions for stick-slip vibration amplitude in friction self-excited model with the stribeck-effect friction model are derived by using Krylov-Bogoliubbov-Mitropolsky method.Moreover,both the stable and the unstable steady-state solutions can be obtained by the analytical expressions.When the stribeck friction mode is employed, the friction self-excited vibration caused by the negative slope mechanism can be obtained, because the kinetic friction coefficient decreases with the increase of velocity,which is unable to be obtained when using the coulomb friction.
Once the self-excited oscillation reaches the steady state, it is obvious that the agreement of the approximately analytical predictions with numerical integration is generally good.The precision of the analytical predictions for the stable steady-state vibration is higher than that for unstable steady-state vibration.The error mainly comes from the harmonic assumption of KBM: the oscillation of the model must have the absolute or approximate harmonic behavior.Obviously,the horizontal stick-slip oscillation of the model in this paper is actually not a strict harmonic behavior.According to the discussions on the influences of the model parameters on self-excited vibration amplitudes, the model can keep the steady state of static equilibrium or the oscillations with a small amplitude if some appropriate parameter values of the variables are chosen,which is helpful to control the friction-induced vibration.
- 船舶力学的其它文章
- Overview of Some Important Factors for Wave Loads and Springing
- Shaping the Structural Frequency Responses with an Improved Partial Eigenstructure Assignment by Minimizing Modal Energy
- An Integrated Design on Next Generation Subsea Production System Based on Multidisciplinary Design Optimization Method
- Expansion Characteristics of Liquid-filled Cell on Hydrodynamic Ram Effect Subject to the Impact of High-speed Projectile
- An Improved Prediction Method for Structural Response Analysis of Offshore Wind Turbines
- Analysis on Plastic Responses of Metal Foam Sandwich Beams under Low Velocity Repeated Impacts

