人工冻结软黏土力学特性试验研究*
曾 宇 白 瑶 孙 鹏 韩天宇
(中国矿业大学(北京)力学与建筑工程学院, 北京 100083)
人工冻结技术广泛应用于富水地层地铁联络通道施工中。在使用冻结法施工时,随着温度降低,土中水结冰后形成强度更高、稳定性更好的冻土,且能达到止水效果,并可作为土体开挖空间的临时支护结构。要解决富水软黏土地层冻结帷幕维护下的联络通道开挖,就必须深入研究冻结软黏土的强度及变形特性,为联络通道冻结法施工提供关键参数。
冻土是由土颗粒、冰体、液相水和气体组成的非均质、各相异性的复杂体系,[1]其力学特性受多种因素影响。国内外学者的研究成果表明,影响冻土强度的因素主要分为两个方面:一是冻土自身性质,即含水率、干密度等;二是来自外界条件,包括温度、围压、应变速率等;这两方面往往相互耦合,共同影响冻土强度。张雅琴等通过研究不同含水率、应变速率和围压等因素对冻土抗压强度影响发现:冻土存在最优含水率,它使得冻土峰值强度达到最大,其抗压强度随应变速率增大而增大、最大偏差应力随围压增大而线性增大。[2-3]诸多学者从以上两个方面出发,研究了不同含水率[4-6]、温度[7-11]、围压[12]、加载速率[13]等对冻土力学特性的影响,取得了丰硕的成果。除此之外,对冻土应力-应变关系的研究是分析其力学特性的关键,其中最具代表性的有以Vialov模型、Duncan-Chang模型为代表的非线性弹性模型和弹塑性本构模型[14]。由于Duncan-Chang模型涉及的数学函数表达式相对简单,参数少且易于测定,在冻土研究领域被普遍采用,但对不同变形阶段的描述仍具有一定局限性。文献 [15-16]针对上述缺陷,提出了修正Duncan-Chang模型,能够比较好地描述岩土体不同阶段的应力-应变特征。综上所述,冻土力学特性受温度、围压、应变速率等影响显著,且土质不同,冻土力学性质也会有所差异。
因此,将以天津地铁7号线富水软黏土地层联络通道冻结法施工为背景,以冻结软黏土为研究对象,对冻结软黏土土样进行不同温度、不同围压以及不同应变速率条件下的三轴压缩试验,研究冻结软黏土典型应力-应变曲线和破坏模式,分析其强度和变形特性,通过对比传统应力-应变关系和改进Duncan-Chang模型,验证改进Duncan-Chang模型的有效性和适用性,为该类地区地铁联络通道冻结法施工方案设计提供参考。
1 土样基本物理参数
试验用土取自天津地铁7号线区间联络通道附近典型软黏土,土体埋深20~25 m。将土样碾碎过筛后进行颗粒级配分析、液塑限测定、击实试验等基本物理力学试验,得到颗粒级配曲线如图1所示,干密度与含水率的关系曲线图2所示,该土样基本物理特性指标见表1。

表1 试验土样基本物理特性指标
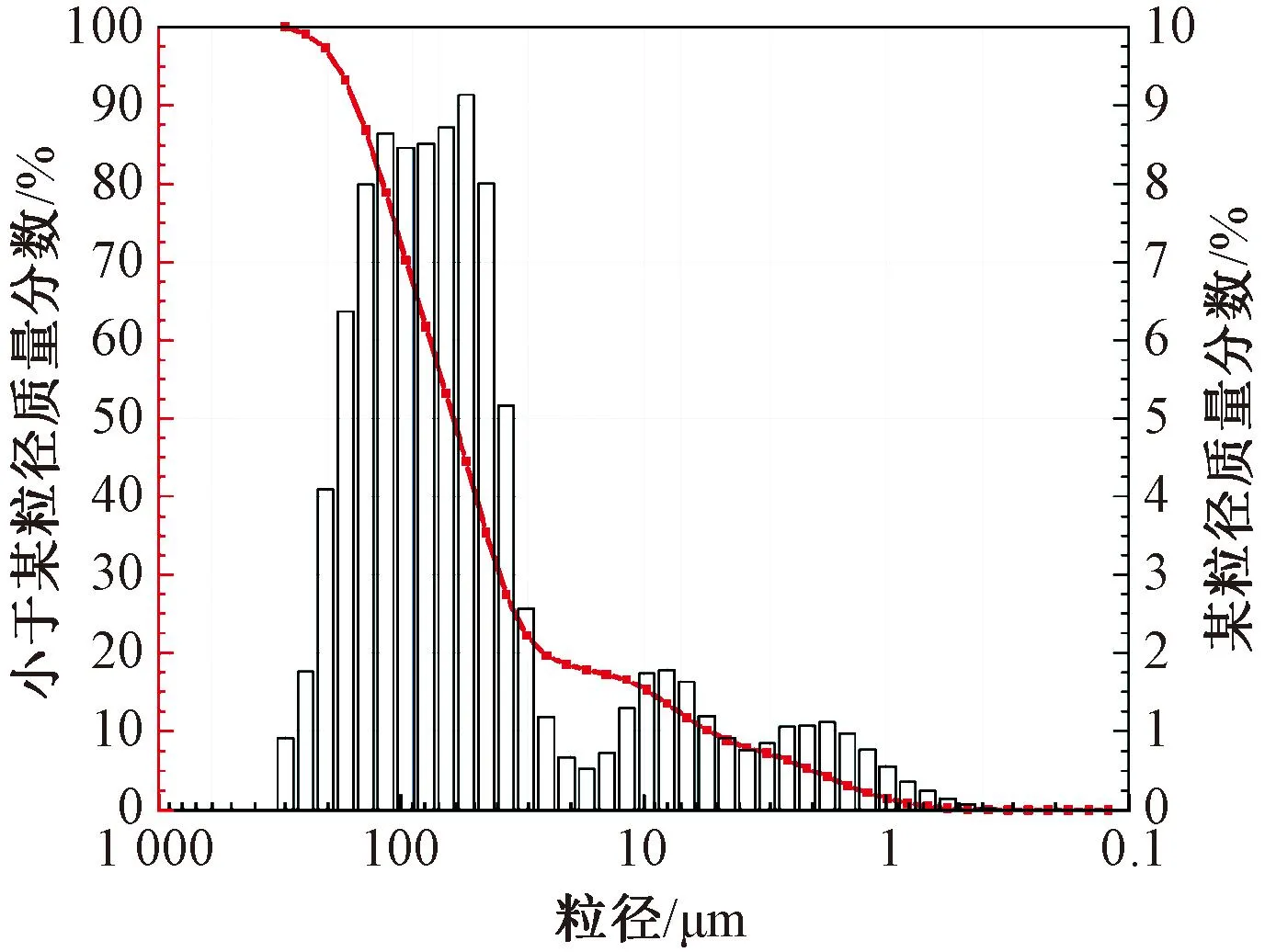
图1 颗粒级配曲线
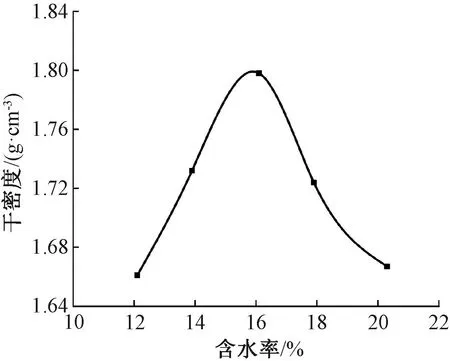
图2 干密度与含水率关系
2 试验准备
2.1 试样制备
试验用的土样均为碾碎过筛后的重塑土,首先将原状土粉碎后过2 mm筛,用烘干箱以105~110 ℃烘干,将烘干后的土配置成设计含水率的土样后密封养护24 h以上,使其水分均匀;然后将湿土分次放入模具击实,将试样连同模具先放于-30 ℃的环境箱内速冻4~6 h后脱模,装入保鲜膜内在试验冻结负温下恒温养护24 h;最后将试样置于低温压力室内再恒温2 h后方可进行试验。
2.2 试验方案
为尽可能接近原状土样的状态,根据重塑土的基本物理特性指标设定重塑含水率,配置了25%含水率的重塑土样。试样尺寸为φ50×100,试验仪器采用中国矿业大学(北京)自主研发的低温三轴试验系统[17],如图3所示。试验时,先将试样从特定冻结负温的冰箱取出,放入容器内,然后将低温储油箱中的冷却油注入容器中,通过调节控制柜和冷却液循环泵使得容器中的试样维持在指定的负温,控制台可以对温度、围压、加载方式进行调节。

图3 低温三轴试验系统
试验加载方式采用应变速率控制,当试样发生破坏或轴向应变达到20%时结束试验。为确保试验结果准确性,每组试验均设置一组对照组。试样制作及试验过程参照MT/T 593.1—2011《人工冻土物理力学性能试验 第1部分:人工冻土试验取样及试样制备方法》[18]和MT/T 593.5—2011《人工冻土物理力学性能试验 第5部分:人工冻土三轴剪切强度试验方法》[19]的要求执行,具体试验方案如表2所示。
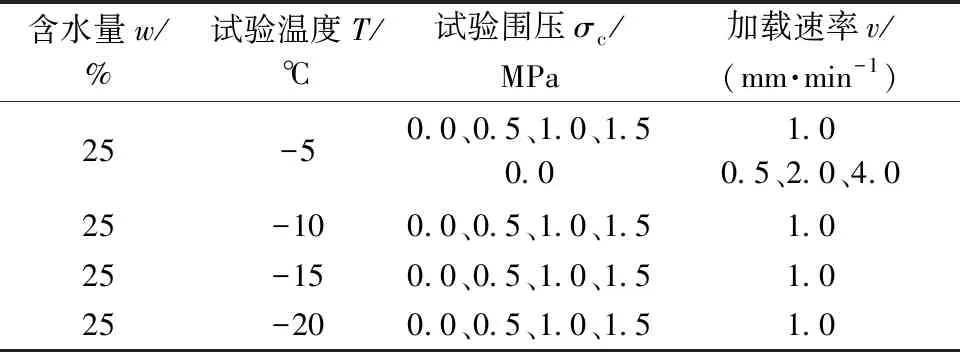
表2 试验方案
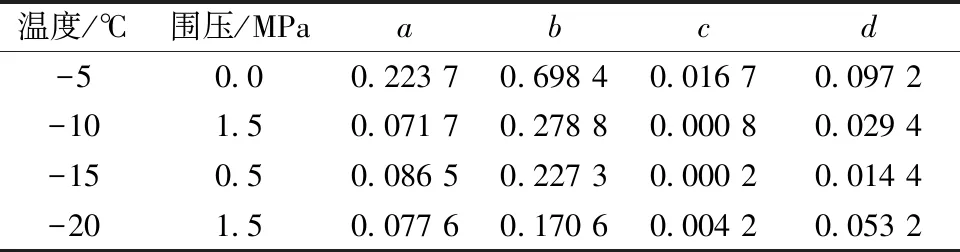
表3 不同试验条件下的模型参数
3 应力-应变曲线与破坏模式
3.1 典型偏应力-应变曲线分析
图4为不同冻结负温、围压条件下冻结软黏土样的偏差应力-应变曲线。可知:试验所得到的偏差应力-应变曲线均表现为应变硬化型。在不同冻结负温、围压下试验曲线主要分为弹性和塑性变形两个阶段,当偏差应力较小时,初期以弹性变形为主。随着偏差应力不断增大,曲线出现了明显的拐点,偏差应力变化缓慢,弹性变形逐渐转变为塑性变形。由于冰的弹性过程相对较短,因此在不同试验条件下弹性区对应的应变基本相同。在相同冻结负温条件下的偏差应力值随着围压的增大也逐渐增大,但随着冻结负温的降低,围压对偏差应力值的影响逐渐降低,如图4d所示,在-20 ℃的环境下,随着轴向应变持续增大,偏差应力增长形态同前,但进入塑性变形阶段的偏差应力值随着围压增大变化幅度极小。原因在于:随着冻结负温的降低,温度对冻土强度的影响增强,土体中未冻水逐渐转化成冰,孔隙被冰填充后增大了黏土颗粒黏结强度,冰的强化效应占主导地位,而围压对试样的强化效应减弱。
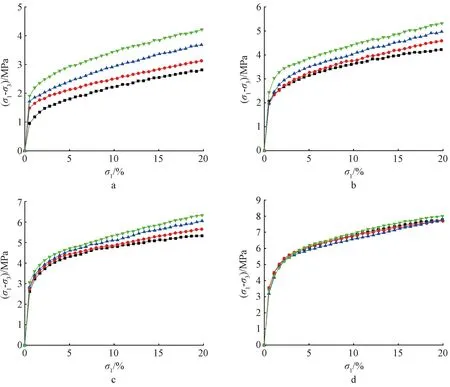
a—T=-5 ℃; b—T=-10 ℃; c—T=-15 ℃; d—T =-20℃。
3.2 破坏模式分析
选取部分试样宏观损伤破坏模式如图5所示。可知:当冻结负温较高时,试样发生鼓胀变形,并未出现明显的破坏面,当冻结负温较低时,试样发生了局部剪切破坏,出现了明显的破坏面,且破坏面呈45°,可见冻结温度、围压对冻结黏土的破坏模式密切相关。
4 影响因素分析
4.1 围压对强度的影响
将图5中数据进行整理、汇总,对于应变硬化型曲线,根据MT/T 593.5—2011[19]取20%应变对应的强度作为试样的抗压强度。图6为不同冻结负温条件下围压与抗压强度关系。可见:对于相同的冻结负温,冻结软黏土的抗压强度随围压增大而增大,且每种冻结负温条件下的围压与抗压强度具有良好的线性关系,可用式(1)进行拟合。拟合结果表明线性相关性较好(决定系数R2>0.99)。从拟合曲线中可以看出:拟合系数M随冻结负温的降低而减小,拟合系数N随冻结负温的降低而增大,同样说明随着冻结负温的降低,围压对试样的抗压强度影响逐渐减弱。
σ1=Mσc+N
(1)
式中:σ1为峰值抗压强度;σc为围压;M、N为拟合系数。
4.2 温度的影响
4.2.1温度对强度的影响
不同围压下的冻结负温与峰值强度关系如图7所示。可知:相同围压下,冻结软黏土的抗压强度随冻结负温的降低而增大,两者呈负相关线性关系,可用式(2)进行拟合。拟合结果表明:线性相关性较好(决定系数R2>0.96),拟合系数A随着围压增大而减小,拟合系数B随着围压增大而增大,表明随着围压的增大,曲线斜率逐渐减小,即冻土的抗压强度对冻结负温的敏感性也逐渐降低。
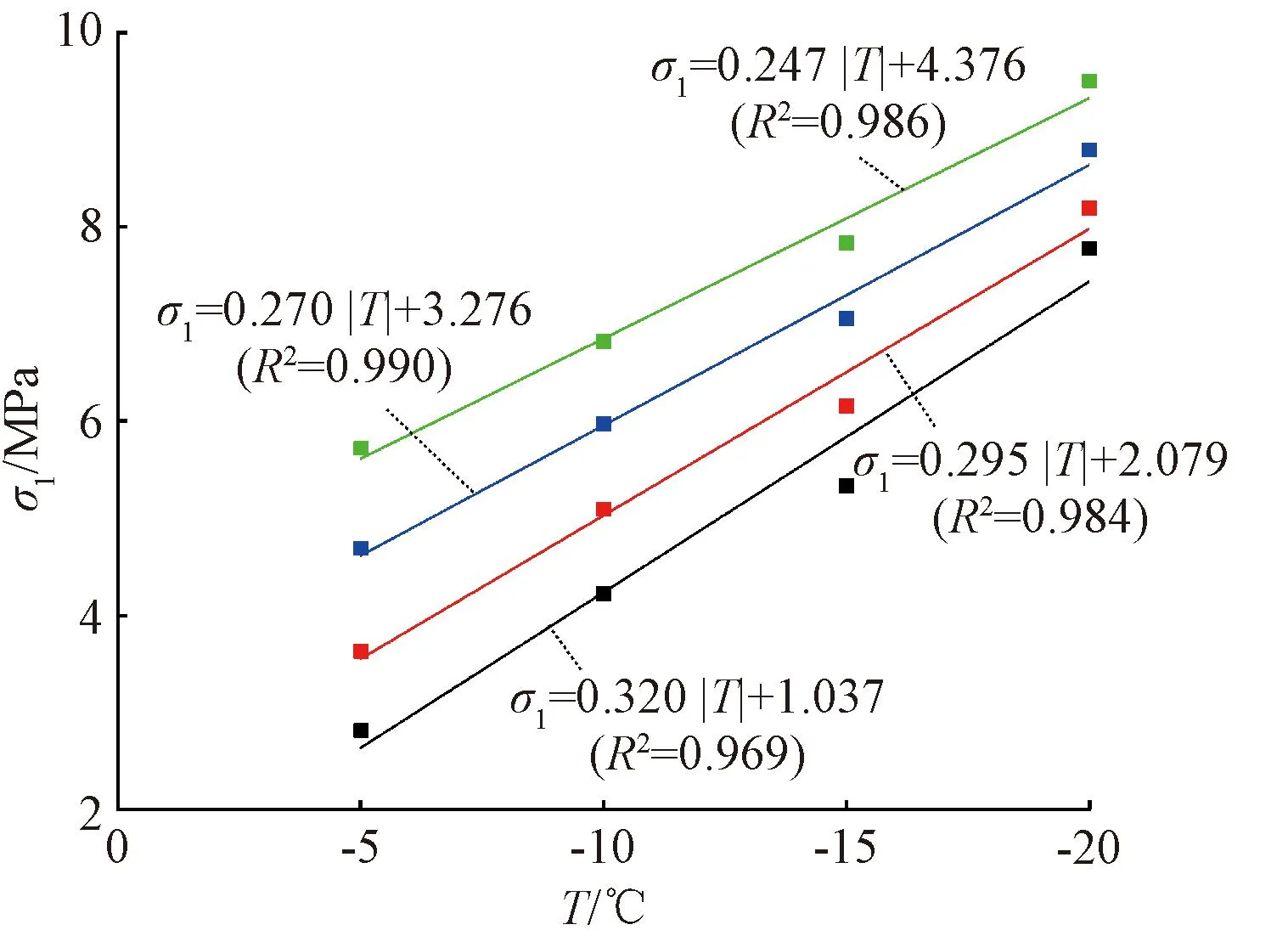
σ1=A|T|+B
(2)
式中:T为冻结负温;A、B为拟合系数。
4.2.2温度对抗剪强度指标的影响
根据摩尔-库仑强度准则得到不同温度、含水率下的摩尔圆与抗剪强度包络线,如图8所示。由抗剪强度包络线可求得不同冻结负温条件下的黏聚力、内摩擦角。两者与冻结负温关系如图9所示。

a—T=-5 ℃; b—T=-10 ℃; c—T=-15 ℃; d—T=-20 ℃。
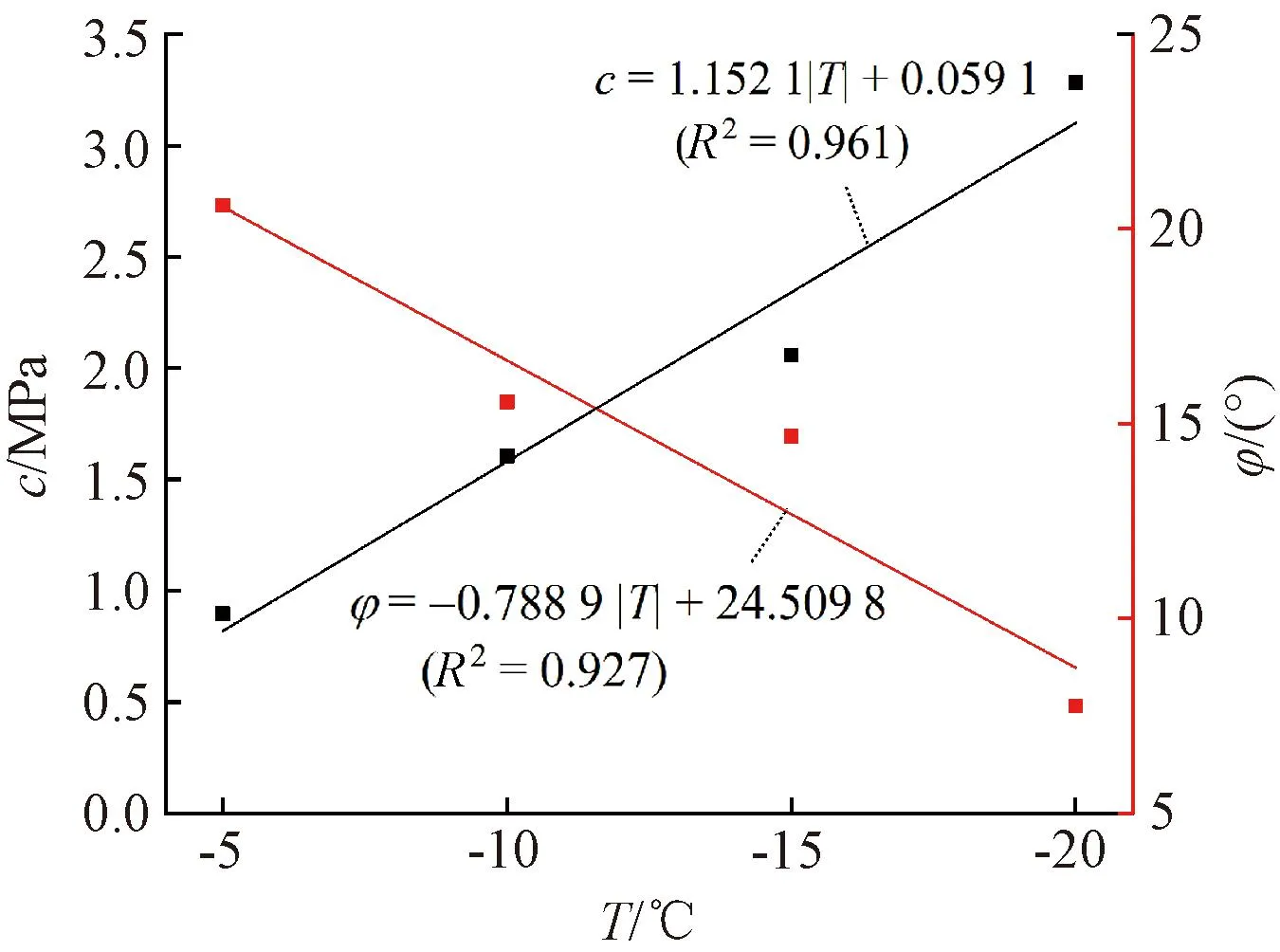
由图9可知:在试验冻结负温范围内,随着冻结负温的降低,黏聚力逐渐增大,内摩擦角逐渐减小。黏聚力变化范围为0.897~3.281 MPa,内摩擦角在7.7°~20.6°,这是由于土颗粒表面凹凸不平,使得土颗粒间的摩擦力较大,随着冻结负温降低,土体内部含冰量增大,除了土体本身的黏聚力之外,冰晶之间会产生更大的黏聚力,使得土体整体的黏聚力增大,此时冰的内摩擦角也随冻结负温的降低而逐渐增大,但随着孔隙中冰含量增大,土颗粒之间的冰晶相对光滑,从而使得试样内摩擦角有所减小。[20-21]同样将黏聚力、内摩擦角与温度拟合可知,两者与冻结负温的线性相关较好(决定系数R2>0.90)。
4.3 加载速率的影响
图10为-5 ℃的环境下,不同加载速率v下的冻结黏土抗压强度变化关系。可知,冻结黏土的抗压强度随着加载速率的增大而增大,通过对试验数据进行幂函数与线性拟合发现,冻结黏土的抗压强度与加载速率更符合幂函数关系,两者关系变化可用式(3)表示,且决定系数R2>0.97,相关性较好。
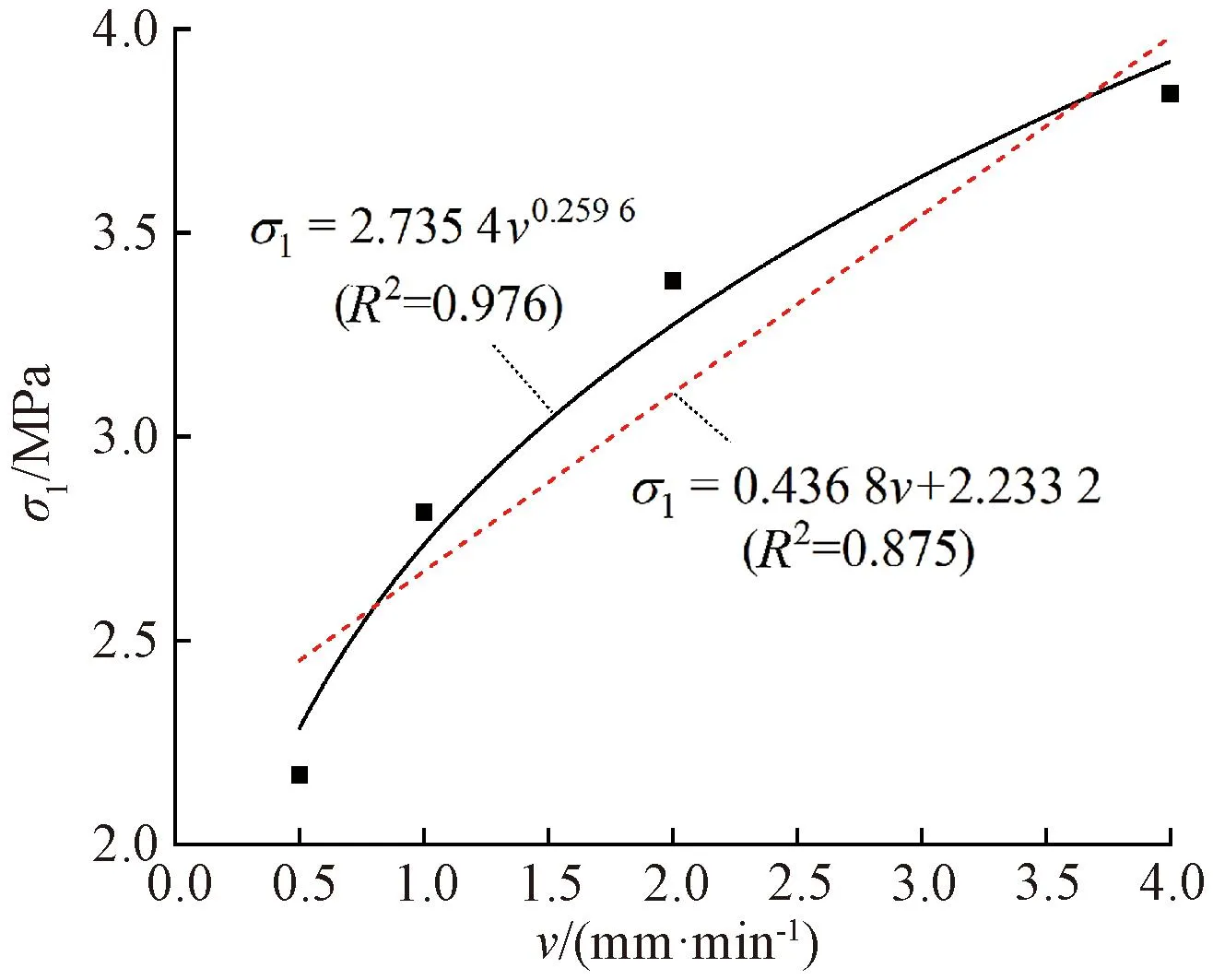
σ1=mvn
(3)
式中:m、n为试验系数。
5 人工冻土应力-应变关系
5.1 典型本构模型[22]
5.1.1Vialov模型
Vialov提出了在恒定应变速率且不考虑围压条件下冻土的应力-应变关系表达式:
σ=Aεm
(4)
式中:σ为冻土试样的主应力;A为试验参数,是速率和温度的函数;ε为冻土试样的轴向应变;m为冻土试样的硬化系数。
该模型适用于描述单轴条件下冻土应力-应变关系,具有一定的局限性,且研究者收集了大量的冻土单轴试验数据,发现Vialov模型无法描述所有冻土体的变形规律。
5.1.2Duncan-Chang模型[23]
Duncan-Chang模型是建立在全量应力-应变试验曲线基础上的非线性弹性本构模型,该模型中采用双曲线方程表示土的(σ1-σ3)-ε1曲线,其表达式如下:
(5)
式中:σ1-σ3为偏差应力;ε1为轴向应变;a、b为材料参数。
Duncan-Chang模型虽然具有形式简单、参数少等优点,但只能描述材料的线弹性和应变硬化阶段,当冻土含水率增大时,对于冻土峰后软化阶段,Duncan-Chang模型不再适用。
5.1.3姜永东模型[16]
姜永东等提出了修正的Duncan-Chang模型,下称姜永东模型,该模型考虑了应力-应变曲线初始压密阶段以及应变软化阶段,该模型的函数表达式为:
(6)
式中:a、b、c为材料参数。
姜永东模型虽然考虑了应力-应变曲线初始压密阶段以及应变软化阶段,却忽略了材料应变软化后的残余强度。
5.1.4改进Duncan-Chang模型
当冻土中含水率较低时,冻结软黏土多数为塑性体,更多地表现出土的性质,其变形为塑性变形;但随着冻土冻结温度降低、含水率增大,冰含量逐渐增加,冻土逐渐表现出冰的脆性变形特性。基于此,白瑶等在前人研究基础上提出一种改进的Duncan-Chang模型[24],改进后的Duncan-Chang模型不仅克服了前面算式存在的缺点,同时继承了上述模型的优点,既能描述材料的线弹性和应变硬化阶段,也可以描述冻土峰后软化阶段。改进Duncan-Chang模型的函数表达式为:
(7)
式中:a、b、c、d为材料参数,且a、c、d均取正。
5.2 模型验证
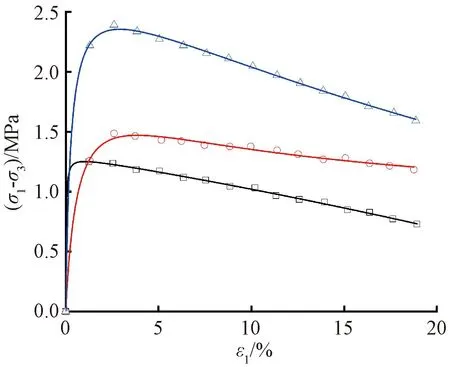
选取4组试验结果对前述四种本构模型进行试验验证,其拟合曲线如图11所示。可知:使用Vialov模型、姜永东模型和改进Duncan-Chang模型均可以描述冻结黏土在不同温度、不同围压下的偏差应力-应变曲线,但改进Duncan-Chang模型拟合效果最好,拟合的决定系数均达到0.99以上,其中部分曲线的模型参数如表2所示。
根据上述结果可知:改进Duncan-Chang模型在拟合冻土的应变硬化特征时取得良好效果。但随着试验条件或冻土种类的改变,冻土也表现出应变软化的特征,为验证改进Duncan-Chang模型对冻土应变软化特征的适用性,使用改进Duncan-Chang模型对文献[6]中高含水量冻粉黏土应力-应变曲线进行拟合,拟合结果如图12所示,可以看出改进Duncan-Chang模型同样适用于描述冻土的应变软化特征,能够准确表征冻结黏土在不同含水率、温度和围压下的变形及强度特性。
6 结束语
通过室内试验,研究了温度、围压以及加载速率对人工冻结软黏土力学特性的影响,主要研究结论如下:
1)在试验条件下,偏差应力-轴向应变曲线均为应变硬化型。随着冻结负温的降低,冻结软黏土由鼓胀变形逐渐转变为局部剪切破坏,其破坏模式受温度、围压、加载速率等影响。
2)在试验冻结负温范围内,冻结软黏土抗压强度与围压呈正相关,与温度呈负相关,均具有良好的线性关系,在较高冻结负温时,冻结黏土强度受围压影响明显,随着冻结负温降低,围压的影响逐渐减弱。黏聚力增加,内摩擦角减小,两者与温度均呈线性相关。抗压强度随加载速率增大而增大,两者更接近于幂函数关系。
3)采用改进Duncan-Chang模型对人工冻结软黏土偏应力-应变曲线拟合可以取得较好效果。

