盐水中法拉第模态的探究

田翠锋，柏圆圆，高彩云，王 萍

（山西大同大学物理与电子科学学院，山西大同 037009）

法拉第波是自由液体表面在垂直振荡驱动下，形成驻波波形图案并以驱动器的一半频率振动的非线性驻波[1]。Rayleigh[2]通过观察验证了法拉第观点，即水驻波振动频率为激励棒频率一半的结论。Benjamin[3]通过分析圆柱形容器中液体垂直振动规律，推导得出Mathieu 方程并证实了法拉第结论。Faraday[4]研究了不同液面波形，观察到了三角形、方形、六边形等形态。液体表面波模态、振幅和频率变化是探究流体从有序流动到混沌运动转变机制，判断稳定性与非稳定性现象阈值等的表征手段，因此探究法拉第表面驻波模态具有重要的理论价值和实际意义。科学工作者研究了表面波模态与激发频率、容器形状或边界条件、液体深度以及液体粘度之间关系[5-11]。在低频驱动下，Jiang[12]在矩形容器中（水深3 cm）发现了凹窝波峰。近期，法拉第不稳定性问题依然是流体力学研究热点之一，Jin[13]应用六自由度晃动矩形容器（水深12 cm）研究高阶法拉第模态，通过快速傅里叶变换方法识别频率反应，发现多模态法拉第波是在多频率激励下触发的。Wilson和Shao[14-15]在圆柱形容器中研究了粘性液体（液体厚度0.7 cm）法拉第波模态，高于法拉第波阈值的驱动振幅会产生次谐波，而低于阈值的驱动振幅会导致谐波边缘波，并给出了多组表面波模态结果。长方形水槽和圆柱形是常用充液容器，两者液体表面波模态和振幅有差别，圆柱形容器模态表现更多样[8,16]。

综上所述，目前的研究中液体表面驻波的驱动频率大多在几十赫兹，讨论驱动源振幅对驻波的影响偏少，因此实验利用高功率数控超声波清洗器作为振荡源头，观察低浓度盐水的表面波模态，通过改变驱动振幅、液体浓度及容器形状探究法拉第波的模态及振幅变化规律，深入了解流体力学驻波物理特性。

1 法拉第波模态理论解释

借助理想流体法拉第波流体力学方程，获得波函数满足的振动方程，分析矩形和圆形两种形状容器下波函数解。通过本征函数法得到Mathieu 方程，进一步获得稳态下色散关系，理解频率与波数、深度、密度和力之间的关系，最后由MATLAB模拟给出不同刚性容器下表面波模态结果。

1.1 法拉第表面波对应的流体方程

一般情况下，描述理想流体法拉第波的流体力学方程[3]为：

其中：g为重力加速度；Fcos(ωt)为振动台垂直振动的加速度；ρ为液体密度；γ为表面张力系数；ξ为竖直方向上位移；φ为流势。根据边界条件可知，ξ、φ可以根据本征函数Sm(x,y)的完全正交集展开：

解方程，获得本征值和本征函数：

其中：l和m包含0 和正整数，分别表示沿x轴和y轴两个方向的波数。MATLAB 模拟波形图如图1，z为波函数Slm。

唐湘如教授在现场介绍了全国以及广东省农业生产中的化肥使用情况，强调平衡施肥、科学种植的重要意义，呼吁在科学指导下合理施用化肥。唐教授带领大家逐一参观各试验处理表现情况，实地向参会者讲解农户常规施肥及不同梯度钾肥施用量对水稻生长发育、产量等的具体差别，介绍钾肥对水稻生产指标的重要影响。

对于边界曲线是半径为R的圆时，使用圆柱形极坐标(r,θ)是很方便的，此时Slm满足

其解为：

其中：klmR是的第m个零点；m为沿圆周分布的整波数；l为方位角模式，沿半径分布的最大值个数。

MATLAB 模拟圆柱形壁波函数分布如图2，z为波函数Slm，图2（a）～（d）为4 个典型模态（m，l）理论示意图，其中，(a)图为(2,0)模态、(b)图为(1,2)模态、(c)图为(2,2)模态、(d)图为(3,3)模态，灰色区域为表面波高于静止水平面，等高线区域为表面波低于静止水平面。

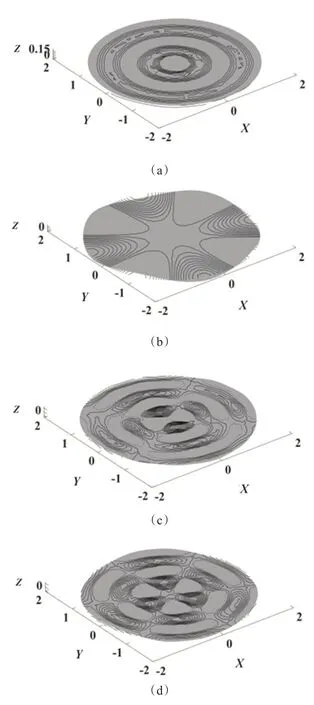
图2 圆形壁波函数分布

以上模拟是稳态结果，当有激励源时，波函数会随时间发生变化。另外，从以上结果可以看出，圆柱形刚性壁表面波模态比矩形容器内模态形状多，这一结论与文献[8]、[16]一致。

1.2 色散关系与模态之间的关系

接下来推导色散关系，利用公式（1），将ξ、φ逐项展开：

这里a0(t)=0，h为液体深度，km为本征值。将（5）式代入（1）式得到：

由于函数Sm(x,y)是线性无关的，所以系数am(t)满足Mathieu方程[3]：

法拉第波出现稳定模态的色散关系不含时间项，由公式（6）可知对应的色散关系为

当频率和外激励满足一定条件时，本征模态会被激发，由此可以导出相应的花纹。表面张力和重力对频率都有影响。由于km=从公式（7）也可以看出，波长与频率不再是线性关系。

2 盐水中法拉第表面波实验

为了给出高频率激励盐水表面波模态，实验选用KQ-600KDE 型高功率数控超声波清洗器作为驱动源，频率为40 kHz，输入功率可以调节到某个固定值，分别为240、300、360、420、480、540、600 W。超声振幅与输入功率关系为

其中：A为超声振幅；P为输入功率；f为超声频率；s为振动面积；α为传输系数。通过计算可知，不同超声输入功率对应的超声振幅分别为106、133、160、186、212、239、265 μm。应用不同驱动功率对低浓度盐水的法拉第波表面波模态进行了定性观测，探究了容器形状、驱动振幅和溶液浓度对法拉第波的影响规律。

2.1 盐水中振动表面波模态观察

2.1.1 同一浓度盐水不同形状容器下表面波模态

对照理论解释部分，实验容器形状选择矩形和圆形截面。为了避免额外的能量耗散和振动迟滞，必须选用刚性容器。矩形刚性容器为超声仪自带容液器，其内槽尺寸长、宽、高分别为30、24、15 cm。圆形容器选用500 mL的烧杯（直径为90 mm）作为充液器，并且烧杯与驱动源之间采用刚性连接。液体选浓度为1%的盐水，驱动源输入功率600 W，通过高速摄像机获得法拉第表面波模态图案，如图3。

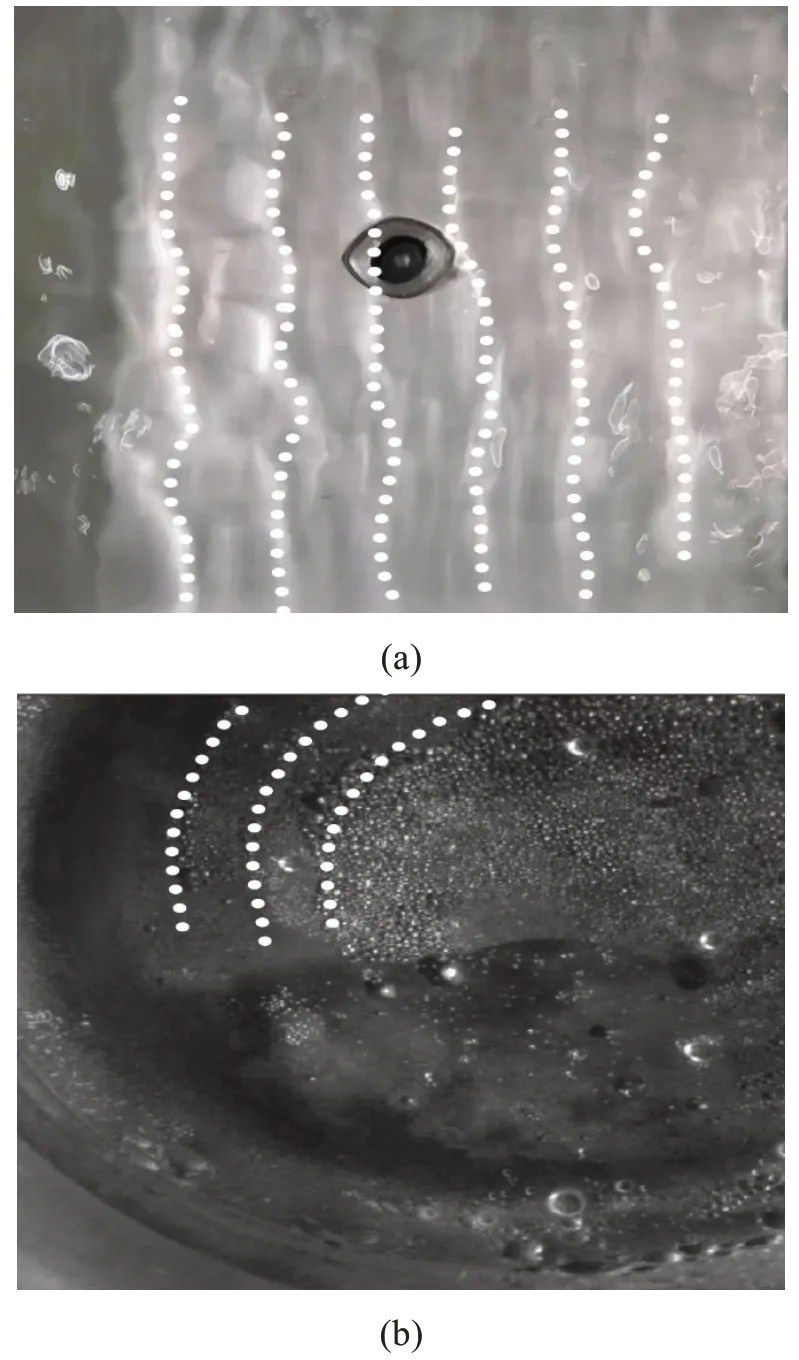
图3 法拉第表面波模态图案

为了更清晰地看到波形，用白色虚线沿着表面波纹描出。从图3（a）可以看出，方形容器的表面驻波模态为条纹状，与图1 波形相似，在出水口出有变形，主要原因是水深落差和边界的影响，另外盐水并非理想流体。图3（b）圆形容器的表面驻波模态为圆环状，与图2（a）模态相似。从波形图来看，图3 与公式（3）和公式（4）所展示的解一致，说明模态结构主要受容器形状影响。为了避免容器内部的高低落差影响，后面的研究选用圆形容器。

2.1.2 同一浓度盐水不同驱动振幅下表面波模态

为了探究激励源振幅变化对盐水表面波模态的影响，实验固定频率，固定盐水浓度，只变化驱动振幅。当驱动振幅从240 W 升至600 W，驻波图案形状无明显变化，但随着振幅增大，形貌更清晰明显。选取驱动功率360 W，盐水浓度为1%质量百分比条件下的驻波图作为展示，图4 为所录视频中的一帧，其规律用白色虚线描画，虚线代表最高峰位置。从图4 可以看出，整体呈圆环状，并且观测到（m，l）=（5，1）振动模态。

图4 功率360W浓度1%时表面驻波模态图

2.2 盐水中振动表面波波幅观察

从垂直角度观察，不同驱动振幅对驻波形状没有影响。从水平角度观察，法拉第波波峰受哪些因素影响，主要从驱动振幅和盐水浓度两个方面探究波幅变化规律。

2.2.1 驱动振幅对法拉第波波幅影响

增大振幅会使所形成的表面驻波图案更加明显，也可通过研究法拉第波振幅变化来证实这一结论。调整高速摄相机的位置、焦距和光强到合适值，使其正好能从侧面看清液面。测量不同功率下法拉第波波峰峰值，振幅高度以水平溶液为基准，如图5，以驱动振幅600 W 盐水浓度1%为例，红色虚线之间为所测波峰峰值，其余振幅和浓度测法类似，所测数据列于表1。

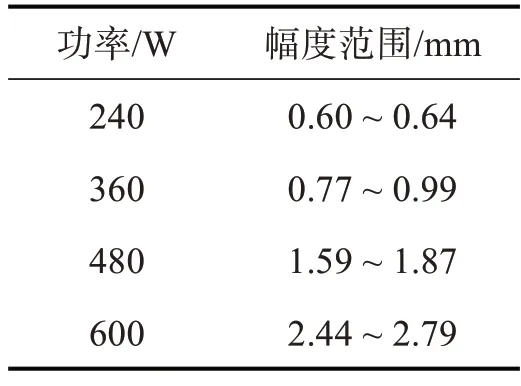
表1 不同功率下表面波振幅变化

图5 功率600W 1%盐水浓度表面波振幅示意图

从表1可以看出，增大驱动振幅会使驻波波峰增大，即法拉第波振幅增大，功率由240 W 增到600 W时，表面波波幅几乎增大4 倍。另外，波峰幅度数量级与文献[8-9]低频驱动下的波高一致，说明高频驱动下，并未引起大幅度变化。

2.2.2 盐水浓度对法拉第波波幅影响

提高激励功率会增大表面波波幅，接下来研究盐水浓度对法拉第波波幅的影响规律。图6 是驱动功率480 W，不同盐水浓度下表面波波幅变化结果。从图6 可以看出，随着浓度增大，表面波波幅最大值有下降趋势，这可能是由于增大盐水浓度会使溶液变得更加黏稠，从而使盐水与烧杯壁之间的黏滞力增大，导致波峰下降。

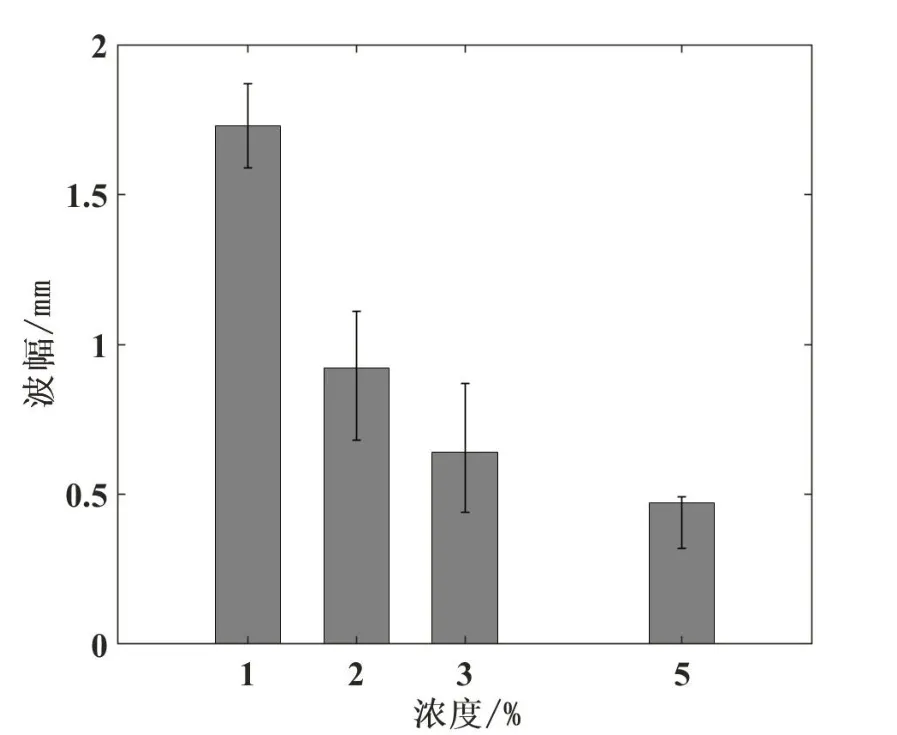
图6 功率480W不同盐水浓度表面波振幅变化图

3 结语

通过MATLAB 模拟和实验分析，对盐水表面波在小振幅（100 μm＜A＜300 μm）高频率超声仪激励下模态进行了研究。通过改变容器形状、驱动振幅和盐水浓度，研究低浓度盐水的法拉第波模态变化规律。根据实验结果分析，矩形容器法拉第波呈现条形状，圆形容器波模态为圆环状，与模拟结果一致。激励振幅变化对驻波形状影响较弱，增大驱动振幅，对应的法拉第波振幅增大，而增加盐水浓度，对应的法拉第波振幅减小。另外，高频驱动并未引起驻波波幅发生量级变化。研究结果对于流体力学领域波动问题的认识和理解有一定的参考意义。