基于多维关联规则的大规模数据并行挖掘研究
赵林燕,雷沁怡,洪德华,孙琦,刘翠玲
(国网安徽信通公司数据运营中心,安徽合肥 230000)
一个由初始向量指向目标向量的映射结果可以用关联系数表示,因此可将多维关联规则理解为由多个关联系数组成的统一集合空间。在由多维关联规则组成的集合空间中,每一个目标向量都对应一个节点,由于关联法则的映射关系不会发生改变,故而目标向量越多,集合空间内包含的节点坐标也就越多[1-2]。对于互联网数据参量而言,基于多维关联规则的集合空间既负责存储映射向量,也能够将相似性向量指标区别开来,一方面使得互联网主机能够对数据进行准确编码;另一方面也可以辅助已编码数据的快速传输,从而便于后续提取与处理指令的快速执行。
数据挖掘是指利用相关算法从海量数据中搜索隐藏信息的方法,按照算法执行条件的不同,可以分为基参量挖掘、并行挖掘、深度挖掘等多种不同的形式[3]。在执行并行挖掘指令的过程中,由于数据离散程度增加,故而极易导致数据分布呈现稀疏情况的出现。为解决上述问题,提出基于信息熵与遗传算法的并行挖掘技术,主要是根据数据节点排列形式建立完整的挖掘指令执行标准,又通过求取决策度指标数值的方式,完善挖掘算法的具体执行流程[4]。然而这种数据挖掘方法在准确挖掘数据参量方面的执行能力有限,实际应用效果并不好。为避免上述情况的发生,提出基于多维关联规则的大规模数据并行挖掘方法。
1 基于多维关联规则的数据集合构造
1.1 关联树结构
该文主要将基于多维关联规则的树状组织作为实现大规模数据并行挖掘处理的基础结构,关联树由多个关联节点组成,但根据执行任务的不同,各个节点所对应的数据对象也有所不同。在图1 所示关联树组织的结构示意图中,“0”节点作为初始结构,负责与互联网存储数据进行对接,并可将待挖掘信息参量直接反馈给下级节点结构[5-6]。“1”节点作为“0”节点的下级附属结构,具备一定的数据分类能力,可以按照数据参量编码形式的不同,将其反馈至不同的存储单元之中。“2”节点~“n”节点作为关联树组织核心处理结构,直接执行数据并行挖掘指令,并可以按照运行处理结果,显示数据信息参量的实时传输位置。

图1 关联树组织的结构示意图
根据关联树组织连接长度的不同,系数“n”的实际取值也有所不同,但在多维关联规则的作用下,树状组织越长,“n”的取值也就越大。
1.2 RFM值计算公式
RFM 值是多维关联规则限定条件,对于互联网数据信息而言,RFM 值指标的计算数值越大,多维关联规则对于数据参量的约束作用能力也就越强。由于关联树结构的连接形式并不会发生改变,故而在求取RFM 值计算公式时,默认相关参量指标的取值结果也不会发生改变[7-8]。设c表示一个随机选取的RFM 值定义指标,且系数c≠0 的不等式条件恒成立,β表示关联树结构中的节点定义系数。联立上述物理量,可将基于多维关联规则的RFM 值计算表达式定义为:
式中,xc表示互联网数据的特征值,αc、δc表示两个不相等的多维向量赋值系数。在求解RFM值表达式时,要求系数xc的取值必须处于[1,e]的物理区间。
1.3 多维运算法则
多维运算法是多维关联规则的执行机制,可以根据RFM 值求解结,确定互联网主机对于信息参量的处理能力。在关联树组织中,反馈节点的排列形式会影响RFM 值计算结果,使多维运算法则的作用能力出现变化[9-10]。设χ表示反馈节点分布系数的初始赋值,其最小取值为自然数“1”。ϕ表示待挖掘数据特征参量,受到RFM 值求解表达式的影响,RFM 值指标的计算数值越大,ϕ系数的实际取值也就越大。在上述物理量的支持下,联立式(1),可将多维运算法则表达式定义为:
其中,b1、b2分别表示两个不相等的信息并行运算特征,表示系数b1与系数b2的平均值,γ表示数据信息提取参量。在构建多维关联规则算法时,要求RFM 指标的计算取值与多维运算法则表达式必须高度统一。
2 大规模数据的并行挖掘算法
2.1 近邻值
近邻值是一个既定取值标签,负责调用多维关联规则,既能够将主机对于数据信息参量的挖掘处理能力控制在合理数值标准之内,也可以分析出待检测信息的分布状态,从而提升网络主机元件提取待测指标的准确性[11-12]。在多维关联规则作用下,近邻值指标的求解要求待测数据取值不能取其物理极限值,即在挖掘指令的单位执行周期内,只能有一个待测数据取值等于极大值或极小值。设a1、ι1表示两个不相等的近邻指标定义项,d1表示待测数据的初始取值,s1表示待测数据分布向量的初始值。
大规模数据并行挖掘算法的近邻值表达式为:
在多维关联规则作用下,近邻值指标取值与逆近邻值指标取值互为相反数。
2.2 逆近邻值
逆近邻值指标可以看作是近邻值指标的补充说明条件,其维度越高,待处理数据信息参量的分布越密集[13]。若将多维关联规则看作非可变应用标准,则可认为在该项约束性法则的作用下,待检测数据的实时存储量越大,逆近邻值指标受到近邻值指标的干扰也就越强;反之,若待检测数据信息的实时存储量较小,逆近邻值指标受到近邻值指标的干扰也就相对较弱[14]。设V′表示多维运算法则V的逆运算函数,且二者之间的取值关系始终满足式(4):
式中,℘表示反函数求解系数。
在数据信息参量逆运算指标恒为d2的情况下,联立式(3)、式(4),可将大规模数据并行挖掘算法的逆近邻值计算表达式定义为:
在求解逆近邻值表达式时,默认近邻值指标、逆近邻值指标互为相反数的条件恒成立。
2.3 离散挖掘系数
离散挖掘系数决定了大规模数据并行挖掘指令的执行能力,在多维关联规则的作用下,待测信息参量的分布离散程度越大,离散挖掘系数的实际取值也就越大[15-16]。考虑近邻值指标、逆近邻值指标的作用同步性,可认为离散挖掘系数的计算取值始终处于(1,+∞)的数值区间。在执行大规模数据并行挖掘指令时,离散挖掘系数同时影响了待测信息参量的并行排列顺序与挖掘运行指令的实际执行情况,且离散挖掘系数越大,待测信息参量的并行排列顺序就越稳定,挖掘运行指令的实际执行等级也就越高。设f表示多维关联规则下的大规模数据离散化排列向量,ΔH表示主机在单位时间内所能挖掘处理的数据信息总量,λ表示待测数据的并行化提取系数。
离散挖掘系数计算表达式为:
至此,完成对各项指标参量的计算与处理,在多维关联规则的作用下,实现大规模数据并行挖掘。
3 实例分析
在互联网环境中,数据信息离散指标的数值水平决定了其分布稀疏程度,这也在一定程度上影响了并行挖掘指令的执行能力。在不考虑其他干扰条件的情况下,数据信息离散指标的数值水平越高,待测信息参量的分布也就越稀疏,此时所得并行挖掘指令的执行能力相对较弱;反之,若数据信息离散指标的数值水平较低,待测信息参量的分布也就相对较为密集,此时所得并行挖掘指令的执行能力相对较强。
表1 记录了实验所选设备元件的名称及相关参量指标的数值情况。
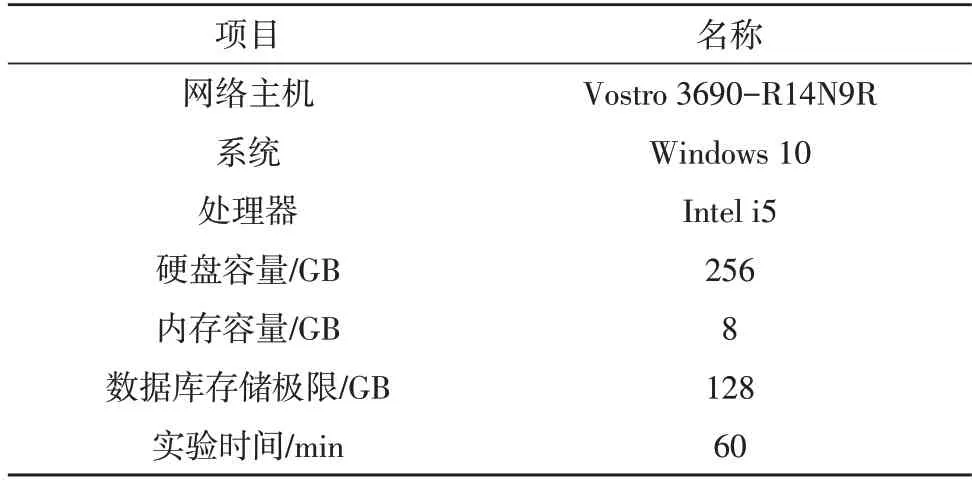
表1 实验参数
具体实验流程如下:
步骤一:利用基于多维关联规则的大规模数据并行挖掘方法对实验主机一进行控制,将所得实验数据作为实验组变量;
步骤二:利用基于信息熵与遗传算法的并行挖掘方法对实验主机二进行控制,将所得实验数据作为对照组变量;
步骤三:对比实验组、对照组变量数据,总结实验规律;
数据信息离散指标的计算式如下:
其中,θ表示并行化离散向量,ω表示挖掘向量定标值。
图2 反映了实验组、对照组ϑ指标与ω指标的数值变化情况。
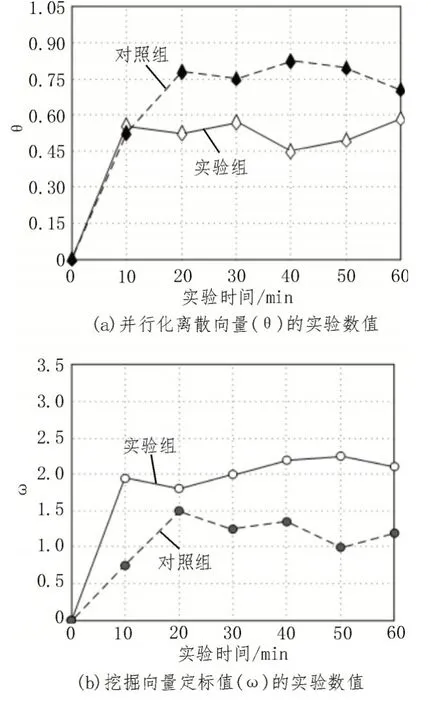
图2 实验数值
分析图2 可知,实验组θ指标的均值水平相对较低,但ω指标的均值水平却相对较高;对照组θ指标、ω指标的数值变化趋势则恰好与实验组相反。
联合式(7)与图2 中的实验数值,对数据信息离散指标μ进行计算,实验详情如表2 所示。

表2 数据信息离散程度
分析表2 可知,整个实验过程中,实验组μ指标的最大值只能达到30.11%,与对照组最大值77.00%相比,下降了46.89%。
综上可知,在基于多维关联规则的大规模数据并行挖掘方法的应用后,数据信息离散指标的数值水平确实得到了有效控制,与基于信息熵与遗传算法的并行挖掘方法相比,该方法可使待测信息参量呈现出较为密集的分布状态,这就表示所得并行挖掘指令始终具备较强执行能力,提升了数据挖掘质量。
4 结束语
为了提升大规模数据并行挖掘质量与效果的问题,提出基于多维关联规则的大规模数据并行挖掘方法,该方法以多维关联规则作为执行基础,在构建树状单元结构的同时,对RFM 指标进行精准求解,又通过对比近邻值指标、逆近邻值指标的方式,计算离散挖掘系数的具体数值,以此实现大规模数据并行挖掘。在实用性方面,在多维关联规则作用下,并行化离散向量指标取值明显缩小、挖掘向量定标值指标明显增大,这对于控制数据信息离散指标的计算数值起到了较强的促进性影响作用,可以在解决因数据离散程度过大而导致的数据分布稀疏问题的同时,获得准确的数据信息参量并行挖掘处理结果,提升数据挖掘质量与效果。

