基于油液在线监测的风机齿轮箱磨损状态识别
靳玉石,刘 伟,张 浩
(1.安徽吉电新能源有限公司,安徽合肥 231200;2.东北电力大学,吉林吉林 132012)
风电装机容量的不断增长,使得风机故障问题越来越成为制约风力资源应用的主要因素。风电机组长期工作在恶劣的自然环境中,各部件的绝缘强度和运行性能将随运行时间的变化而逐渐下降[1]。齿轮箱作为风机的关键部件,其故障运维会增加巨额维修成本且因故障导致的停机时间最长[2]。利用齿轮箱油液信息来诊断风机齿轮箱早期故障,可以降低风电场运行成本,提升效益。
该文提出一种基于在线监测的油液信息识别风机齿轮箱磨损状态模型,该模型利用BP 神经网络在识别诊断方面的优势,通过训练学习,综合分析多种油液信息获取齿轮箱磨损状态,避免由单一油液信息导致的诊断准确率较低的影响,提高了风机齿轮箱监测的可靠性,为风机运维提供科学依据。
1 BP神经网络
BP 神经网络是一种误差反向传播的前馈型人工神经网络,是目前应用最广泛的神经网络模型之一。该模型具有强大的信息处理能力以及自适应学习能力,在控制、图像识别、信号处理、非线性优化等领域得到广泛应用[3]。
典型BP 神经网络有三层结构,即输入层、隐含层、输出层,计算方式主要有输入信息正向传播和误差信息反向传播[4]。
BP 神经网络输入信息正向传播计算过程如下:
BP 神经网络隐含层和输出层神经元输出分别为:
式中,n、m分别为输入层和隐含层节点个数;ω和θ为BP 神经网络输入层到隐含层连接的权值和偏置值;ω′和θ′为BP 神经网络隐含层到输出层连接的权值和偏置值;x为BP 神经网络的输入层的输入;HO为BP 神经网络的隐含层神经元输出;f′(x)为输出层神经元的激励函数。
BP 神经网络模型的训练过程:通过不断调整每一个权值和偏置值来降低模型预测的误差大小,误差信息反向传播过程如下:
隐含层和输出层权值梯度分别为[5]:
因此,各层的权值和偏置值的更新公式如下:
式中,ωn和ωn+1分别为各层神经元第n次和第n+1 次迭代的权值;θn和θn+1分别为各层神经元第n次和第n+1 次迭代的偏置值;ε为网络学习率;E为网络训练误差。
2 齿轮箱磨损状态识别模型
风机齿轮箱润滑油液携带大量关于齿轮磨损等早期故障的特征信息。随着润滑油使用时间的增加,齿轮部件表面摩擦产生的金属颗粒和其他杂质会进入油液中,导致润滑油变质[6]。通过油液监测技术,可以获取有关齿轮箱磨损状态信息,预测和诊断齿轮箱故障[7]。传统齿轮箱故障诊断方法有铁谱分析法[8]、支持向量机[9]、自回归滑动平均模型[10]、改进的Elman 神经网络[11]、K-means 聚类[12]等。风机油液监测可以发现齿轮箱的潜在故障威胁[13],能够判断齿轮箱的润滑和磨损状态[14],可以极大地提高设备的运行可靠性。
该文选择润滑油液的粘度、水分、污染度、磨粒信息以及介电常数作为风机齿轮箱磨损状态识别的特征值。构建BP 神经网络的风机齿轮箱磨损状态识别模型,使用不同磨损状态类型的风机齿轮箱油液数据作为输入样本,将磨损状态类型作为输出来实现磨损状态的识别。磨损状态可划分为正常运行、轻微磨损、异常磨损、严重磨损、失效停机五种类型[15]。网络模型训练中对五种磨损状态进行编码,如表1 所示。

表1 齿轮箱磨损程度编码
基于BP 神经网络的风机齿轮箱磨损状态识别方法,在本质上是一种故障分类问题。将提出的BP神经网络模型用于风机齿轮箱磨损状态识别,将风机齿轮箱油液数据和对应磨损状态类别标签组成的实验数据划分为训练集和测试集,利用训练集数据训练该文所提出的BP 神经网络模型。网络模型识别流程如图1 所示。

图1 网络模型识别流程
网络模型识别的具体步骤如下:
1)根据油液参数以及输出磨损状态类型个数确定BP 神经网络的结构;
2)对油液样本数据进行归一化处理,使其符合网络的输入条件;
3)初始化网络权值与偏置;
4)将训练集样本输入神经网络;
5)开始网络学习,计算网络模型误差,更新网络权值与偏置;
6)判断误差是否满足终止条件,若否,则返回第4步;若是,则输出BP 神经网络最优结构;
7)利用训练好的网络模型对测试集样本进行识别。
3 算例分析
3.1 数据预处理与参数设置
由于不同的油液信息有不同的单位、大小以及量纲值,因此对于神经网络模型输入的油液信息采用以下公式进行归一化:
式中,y为归一化后的样本数据;xmax、xmin分别为样本数据最大值和最小值。
BP 神经网络隐含层的节点数会对模型的训练精度与识别结果产生的一定的影响,但是隐含层节点数没有固定的确定方法,该文根据以下公式来确定范围:
式中,n为输入节点数,m为输出节点数,a为[0,10]之间的常数。由此确定,BP 神经网络隐含层节点数范围在[3,13]之间。由实验确认,当隐含层节点数为5 时,BP 神经网络模型的训练误差最小,训练精度最高,因此确定该文提出的BP 神经网络隐含层节点数为5。
3.2 实验分析
选用某风机齿轮箱各磨损状态下的油液数据共计2 500 组作为实验样本,样本包括训练集和测试集,取10%的样本作为测试集。将归一化后的训练集数据输入BP 神经网络模型进行网络训练。图2 为BP 神经网络训练交叉熵损失函数曲线。
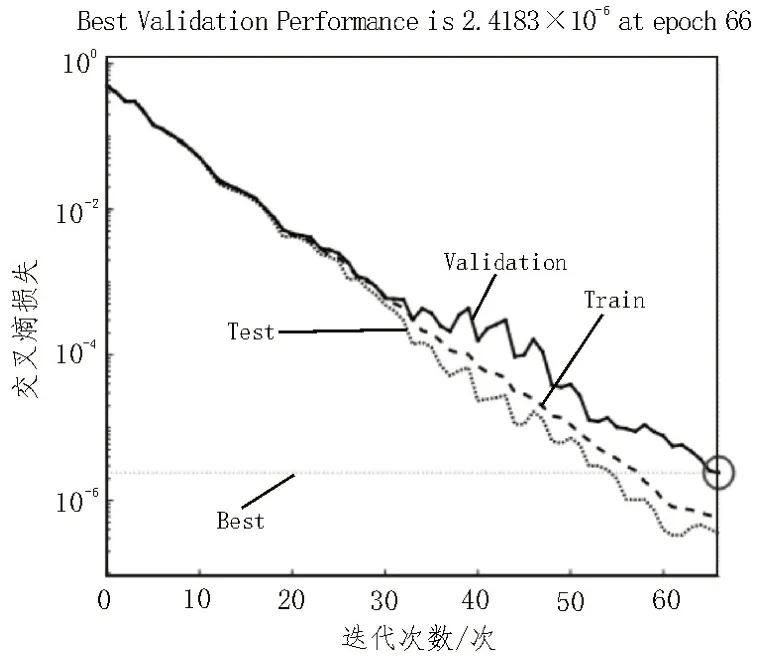
图2 BP神经网络模型训练误差曲线
从图2 中可以看出,BP 神经网络训练模型经过66 次迭代达到最佳验证性能点,此时的交叉熵误差函数值为2.418 3×10-6。通过混淆矩阵给出模型的训练结果,如表2 所示,混淆矩阵横坐标为目标输出,纵坐标为实际输出。由此可以看到,在2 250 组训练样本中,样本的训练结果准确率为99.6%。

表2 BP神经网络模型训练样本仿真结果
为验证BP 神经网络模型的性能,在经过训练后,将测试样本输入模型进行磨损状态识别。模型识别结果的混淆矩阵如表3 所示,分析250 组测试样本的识别结果,在五种磨损状态的实验分析中,每种磨损状态的识别结果均在96%以上。由此可知,BP神经网络模型的整体识别准确率为98%。
3.3 对比实验分析
K 均值聚类是将样本划分为K个簇的动态聚类方法,使划分到每个簇的样本是相似的,以达到分类的目的[16]。K 均值聚类算法具有操作简单、聚类效果好等特点,在群体分类、数据处理、故障诊断等方面得到了广泛的应用。
为对比该文提出的BP 神经网络模型与其他算法的识别性能,将测试集样本通过K 均值聚类算法进行磨损状态识别。图3 为BP 神经网络和聚类算法对测试集样本在不同磨损状态下的识别准确率。由图3 可以看出,在5 种磨损状态类型识别中,该文所提出的BP 神经网络模型的识别准确率均高于传统聚类算法。
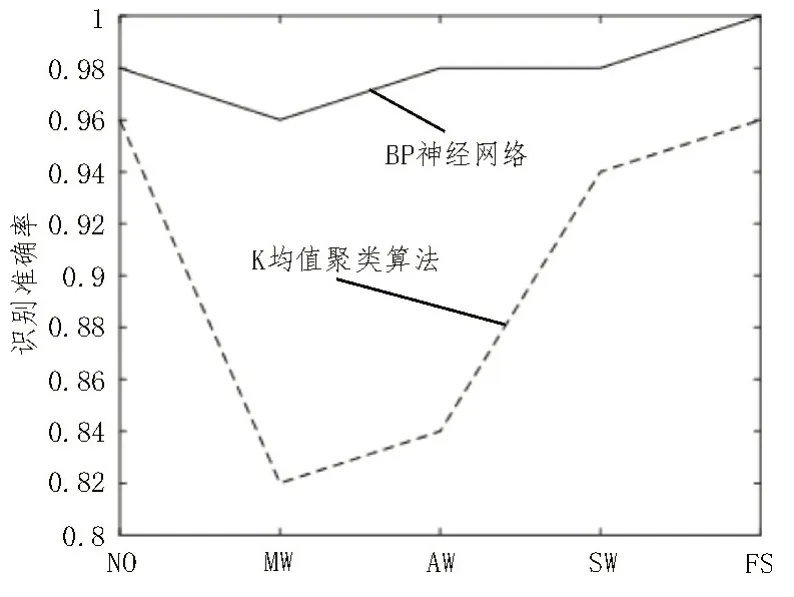
图3 不同模型对磨损状态的识别结果
在不同磨损状态类型的识别中,BP 神经网络模型具有较强的识别稳定性,每种磨损状态的识别准确率均保持在96%以上。表4 是BP 神经网络对于风机齿轮箱磨损状态的识别结果。由表4 可看出,对不同程度磨损状态样本进行测试,BP 神经网络模型均可以准确地识别磨损状态类型。
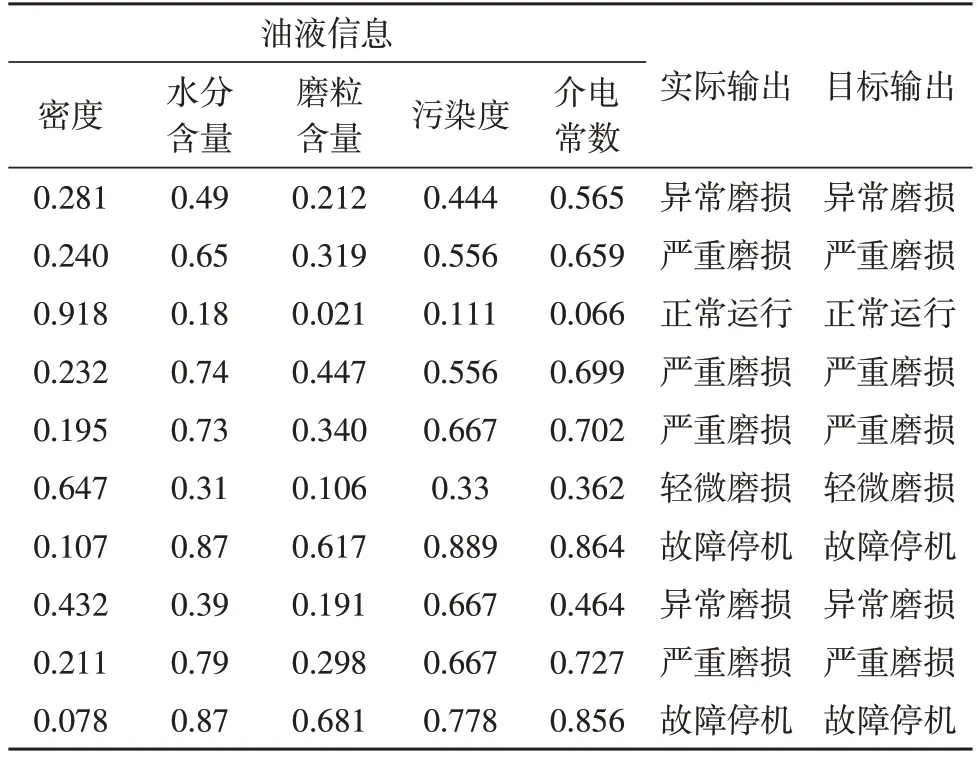
表4 样本的BP神经网络模型归一化识别结果
4 结论
针对离线油液监测风机齿轮箱故障的缺陷与传统聚类算法识别风机齿轮箱磨损状态准确率较低的问题,该文利用BP 神经网络模型基于在线油液监测的数据样本识别风机齿轮箱磨损状态。对算法进行测试,识别准确率达到了预期,为今后进一步深入研究基于在线油液监测的风电机组齿轮箱故障诊断提供了新思路。

