分形超晶格结构晶体中的多波长频率转换
王雪颖,马博琴
(1 中国传媒大学 信息与通信工程学院,北京 100024)
(2 中国传媒大学 数据科学与智能媒体学院,北京 100024)
0 引言
激光器产生的波长受到增益介质中原子、分子或者离子的能级结构限制,很多波长不能直接产生,因此非线性频率转换有着十分重要的使用价值。要实现高效率的非线性频率转换,需要解决光波在介质传播中的相位失配问题。解决相位失配问题主要有两种技术:双折射相位匹配技术和准相位匹配技术。传统的双折射相位匹配技术[1]在实现相位匹配的过程中,对温度和角度有着严格的要求,因此在非线性光子晶体的应用上存在局限。准相位匹配技术[2]可通过在介质区域内进行畴反转,借助其倒空间中的倒易矢量来弥补相位失配,进而来提高频率转换效率、拓展激光波长范围。在准相位匹配技术产生谐频的过程中,若基频波矢与倒易矢量共线,则该过程称为共线准相位匹配,否则,称之为非共线准相位匹配。光学超晶格[3-4]作为二阶非线性光学效应的载体,是非线性光学领域的重要研究领域之一。YAMADA M 等[5]在室温的条件下通过外加电场极化技术制备了厚度为0.2 mm、周期为2.8 μm 的超晶格铌酸锂晶体,实现了功率为20.7 mW 的蓝色光束,其转换效率高达600%/W·cm2,因此准相位匹配技术迎来了真正意义上的发展和应用。随着对准相位匹配技术和光学超晶格结构的深入研究,在一个超晶格器件中实现单一波长的准相位匹配过程已经无法满足人们的需求。CHOU M H 等[6]突破了周期光学超晶格结构,提出了一种双周期相位反转结构,实现了双通道、三通道、四通道的二次谐波输出。随着研究的拓展,准周期结构得到了广泛的关注。南京大学团队[7]提出了一种基于斐波那契数列的准周期光学超晶格结构,能够同时实现了多波长的二次谐波。我们研究小组已对H 型分形、谢尔宾斯基分形等超晶格结构[8]进行了研究,并制备了相应的非线性光子晶体,不同的超晶格结构晶体在非线性光学效应中有着各自的现象。
为了探究不同的超晶格结构的优势,越来越多的超晶格结构应用到光学材料中,以产生不同波长的谐波[9-11]。光学超晶格结构的设计也从最初的周期结构发展到准周期、啁啾、分形等多种结构,例如同心环形超晶格[12]、椭圆超晶格[13]、向日葵螺旋超晶格[14]、径向超晶格[15]等结构。超晶格结构的设计对于激光的发展具有重要的意义,能够补充激光器输出频谱的空窗波段,满足实际应用中的需要。Gosper 分形和Z 分形都是由一条线构成的二维平面图,在空间索引[16]、数学规划[17]、新型天线结构设计[18-19]等方面具有较高的研究价值。基于以上研究,本文提出了将Gosper 分形与Z 分形结构分别引用到非线性光学超晶格的构想,分析了两种分形超晶格结构可实现的谐波波长及其特性。
1 二维分形超晶格结构设计
Gosper 分形与Z 分形结构具有自相似的特性,都是由一条连续不间断的空间填充曲线构成。在分形结构中,分形维度是描述该分形结构不规则的量度,通常用豪斯多夫维数D=lnN/ln(1/r)计算,其中N表示每迭代一次自相似图形复制的个数,1/r表示曲线长度缩放的比例。在区域一定的情况下,分形迭代次数越高,占空比就越高,超晶格结构就会越紧密,其倒空间中的倒格矢就会越丰富,因此分形维度、占空比两个参数对分形超晶格结构的选择具有正向引导的作用。
1.1 Gosper 分形超晶格结构设计
Gosper 分形曲线可由L-系统[20]表示,L-系统的规则是对n阶分形编码进行替换,产生n+1 阶的分形编码。假设Gosper 分形曲线的初始编码“A”为一条任意位置和方向的线段,其决定了Gosper 分形曲线的初始位置和初始角度,编码的替换规则[21]为:“A”替换为“A-B--B+A++AA+B-”,“B”替换为“+A-BB--BA++A+B”。其中“A”和“B”表示向前移动相同的距离,“+”代表顺时针旋转60°,“-”代表逆时针旋转60°。图1(a)为二阶Gosper 分形曲线,是由7 个一阶Gosper 分形曲线组成的。分形每迭代一次,其迭代后的面积是迭代前的7 倍。在迭代过程中,n阶Gosper 分形曲线各个方向的维度是n-1 阶的倍,例如:二阶曲线的首尾线段长度是一阶曲线的倍,因此Gosper 分形的豪斯多夫维数为。
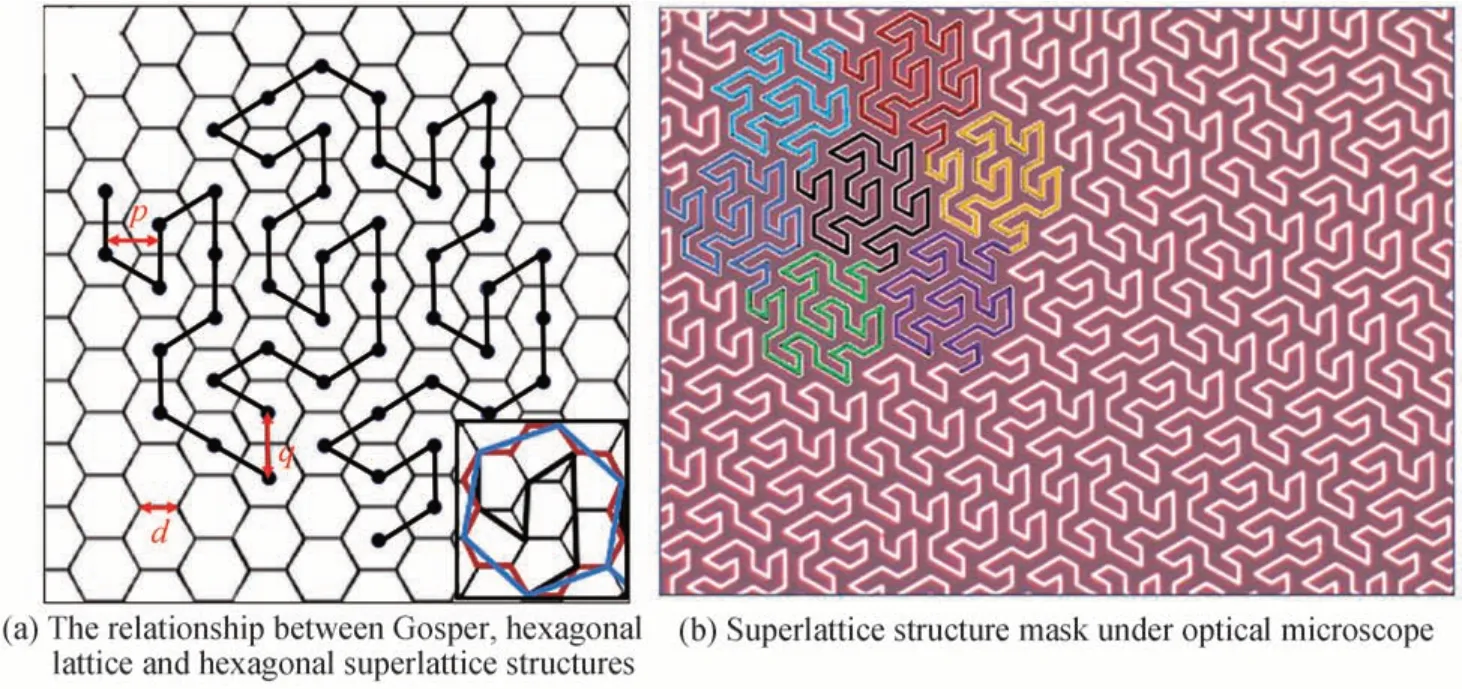
图1 Gosper 分形超晶格结构设计Fig.1 Structure design of Gosper fractal superlattice
与其他分形不同的是,Gosper 曲线还具有边界分形的特性,这也意味着Gosper 分形曲线比其他分形曲线更具有复杂度。为了更好描述Gosper 曲线的边界分形,将其引入到正六边形中进行描述,形成规则为:将边长为x的正六边形每条边都用3 条起伏的折线来代替,可得到18 条长度为的线段;将此时的18 条线段再次用长度为x/7 的3 条折线代替,依此类推,重复迭代的次数越多,形成的Gosper 分形的边界就越精细。如图1(a)中的右下角所示,一条蓝色直线是由三条红色折线组成,且蓝色直线长度是红色直线的倍。因此,其边界分形的豪斯多夫维数为。Gosper 分形曲线的两种分形维度(整体分形维度、边界分形维度)体现了其具有复杂的空间结构。
为了对Gosper 分形超晶格结构有更好的研究,另外设计了六角点阵、六边形两种周期结构,这两种周期结构和Gosper 分形超晶格结构三者的正空间结构关系如图1(a)所示,其中,六边形周期结构为底,六角点阵位于六边形周期结构的中心部分,Gosper 分形超晶格结构则是把六角点阵按照L-系统规则进行连线。在设计超晶格结构掩模版时,为了保证波长的转换效率以及避免极化过程中的畴扩展产生的影响,将Gosper 超晶格结构的空间间距p设置为13.64 μm,线宽设置为3 μm;六角点阵的周期q设置为15.75 μm,直径设置为3 μm;六边形的边长d设置为9.094 μm,线宽设置为3 μm。在掩模版制作完成之后,为了确定超晶格结构的完整性和正确性,在光学显微镜下对掩模版超晶格结构进行检测,如图1(b)所示,左上方为7 个不同颜色的二阶分形构成的三阶Gosper 分形。
1.2 Z 分形超晶格结构设计
Z 分形曲线也称Lebesgue 曲线,是一条连续、自身没有交叉的空间连续曲线。图2(a)为Z 分形曲线的结构示意图,假设二维空间的长度为L,宽度为W,把空间划分为23×23个长方形,3 阶Z 分形曲线可以穿过大小相等、互不重叠的64 个网格,在空间区域一定的情况下,曲线的阶数越高,空间网格分割的越细。图中红色框内为一阶Z 分形曲线,是由编码0~3 顺序连线构成,曲线的拐点为长方形的中心。在此基础上进行迭代一次,面积复制为原来四倍,四部分进行首尾相接,得到蓝色虚线框内编码为0~15 的二阶Z 分形曲线,按照这样的方法循环下去,就可以得到n阶Z 分形曲线。综上,Z 分形曲线的豪斯多夫维数D=ln 4/ln 3=1.262。

图2 Z 分形超晶格结构设计Fig.2 Structure design of Z fractal superlattice
在光学显微镜下的掩模版超晶格结构如图2(b)所示,在Z 分形超晶格结构掩模版的设计中,将其空间间距设置为13.64 μm、27.28 μm,为了防止在极化过程中畴反转面积扩延,失去超晶格结构原本的规则形态,线宽设置为3 μm。
2 实验结果分析
2.1 Gosper 分形超晶格结构
光的衍射在数学上是二维傅里叶变换的一种直接体现。本文用Matlab 设计了一个模拟超晶格衍射图的仿真程序,在制作掩模版并进行衍射实验之前,对其倒空间分布情况进行分析。图3(a)左部分为Gosper分形超晶格结构的模拟衍射图,右部分是波长为532 nm 的半导体激光束垂直入射至超晶格结构掩模版所获得的实验衍射图,两者完全吻合。图3(b)为六角点阵(左)、六边形(右)周期结构的衍射图,右上方插图为掩模版部分结构图,其中黑色区域为透光部分。

图3 Gosper 分形与周期结构超晶格衍射图Fig.3 Diffraction patterns of Gosper fractal and periodic structures
为了更好观察六角点阵周期结构、六边形周期结构和Gosper 分形超晶格结构三者在倒空间中的关系,在衍射实验中,掩模版到衍射屏的距离均为25 cm。从三者的衍射图中可以看出,六边形的衍射图案比六角点阵更亮,这主要是因为六边形光栅占空比更大。由于两种周期结构衍射图的中心部分相同,衍射亮斑整体都是呈六边形结构,且相邻衍射亮斑之间的距离均为1.00 cm,这意味六边形周期结构能够提供与六角点阵相同的倒格矢大小,实现相同基波波长的倍频输出。不同的是,在六边形周期结构的衍射图中,存在六个相同的锥形结构延伸部分,两个相邻锥形结构之间的角度为60°,体现了六边形周期结构在高阶准相位匹配时比六角点阵具有一定的优势。Gosper 分形超晶格结构的衍射图不再像六角点阵与六边形结构存在有序周期分布,其结合了六边形、六角点阵两个周期结构衍射图的相同之处,即中心部分是包络结构,且同阶级衍射点可以构成一个等边六边形,同时也将两个周期结构的不同之处体现了出来,即整体分布着六条衍射亮线,相邻两条衍射亮线之间的角度为60°,这意味着能够在六个不同方向同时实现同一波长的谐波转换。此外,衍射亮线上的相邻衍射亮斑之间的距离几乎是一致的,每一个衍射亮斑周围都围着相对应的六个次亮斑,体现了分形的局部与整体的相似性。值得注意的是,远离中心的衍射斑点依然很亮,说明Gosper 超晶格结构在实现高阶衍射时具有很大的优势。Gosper 分形衍射图顺时针旋转90°的中心部分与南安普顿大学研究的高阶Gosper 分形结构的电子衍射图[22]完全吻合。
为了更好的计算Gosper 分形中的倒空间分布,将其中心部分的衍射强点划分为六个六边形结构,为使倒空间结构更加清晰,图3(c)中仅展示了三个,如图所示,定义了a、c两种大小的倒易基矢,b可以由a和c进行线性组合得到,这三个矢量可以表示Gosper 分形倒空间中的大部分的衍射亮斑。在掩模版到衍射屏的距离为25 cm 的情况下,|a|、|b|、|c|的大小分别为0.64 cm、1.05 cm、0.41 cm,误差在5%以内。Gosper 分形超晶格结构的倒空间存在着多个不同大小的空间距离,每个空间距离都有与之相等、六个不同方向的衍射强点相对应,考虑到铌酸锂晶体的通光范围以及转换效率,选取的衍射斑点与中心点的距离分别为|a|、|2a|、|b|、|2b|、|3b|、|2c|、|3c|。
本文以铌酸锂非线性光子晶体为例进行理论计算,其通光范围在0.4~4.5 μm 之间,覆盖了近中红外区域。六角点阵超晶格结构的倒格矢大小可表示为,C0是六角点阵正空间周期,大小为15.75 μm,m、n分别为倒易矢量在水平、竖直方向的阶数。当(m,n)为(1,0)时,|G1,0|为0.399 μm-1,将倒格矢大小|G1,0|代入铌酸锂晶体的Sellmeier 公式,在共线的条件下可实现波长为1.430 μm的倍频输出。
已知六角点阵超晶格结构的倒易矢量分布,分形超晶格结构的倒易矢量分布可基于超晶格结构衍射图计算法[8]得出。根据六角点阵的周期为15.75 μm,倒易矢量为0.399 μm-1,可得到Gosper 超晶格中衍射亮斑对应的倒格矢大小。如图3(c)所示,衍射亮斑到中心点的距离为|a|=0.64 cm,倒格矢大小为|Ga,1|=0.255 μm-1,其表示为a方向上一阶倒格矢的大小;衍射亮斑到中心点的距离为|2a|=1.28 cm,其倒格矢大小为|Ga,2|=0.511 μm-1。将得到的倒格矢理论值代入动量守恒公式,可理论计算出入射基波波长。在共线准相位匹配的条件下,基频光沿a的方向入射能够通过倒格矢|Ga,1|=0.255 μm-1、|Ga,2|=0.511 μm-1的相位补偿,产生882.5 nm、650.5 nm 的二次谐波;沿b的方向入射能够通过倒格矢|Gb,1|=0.419 μm-1、|Gb,2|=0.838 μm-1、|Gb,3|=1.257 μm-1的相位补偿,产生701.5 nm、549 nm、483.5 nm 的二次谐波;沿c的方向入射能够通过倒格矢|Gc,2|=0.327 μm-1、|Gc,3|=0.491 μm-1的相位补偿,产生778.5 nm、660 nm 的二次谐波。综上可知,Gosper 分形超晶格结构中有更多更灵活的倒格矢,可以实现多个范围内的频率转换。
图4 为Gosper 分形超晶格结构的非共线准相位匹配过程。共线准相位匹配通过不同的倒格矢仅能够实现离散波长的倍频,不能展现出二维非线性光子晶体中全部可实现的波长转换。例如,在共线准相位匹配中,倒格矢Gb,1、Gb,2、Gb,3可实现离散基波波长1.403 μm、1.098 μm、0.967 μm 的倍频,由表1 可知,非共线准相位匹配可通过倒格矢0.838 μm-1、1.257 μm-1实现基波波长为1.143 μm、1.011 μm 的倍频,该过程能够补充共线过程中1.403 μm~1.098 μm、1.098 μm~0.967 μm 波段的空缺,增强波长的可协调性。此外,在非共线准相位匹配中,可以充分利用入射基频光方向与倒格矢方向之间不平行的特点,使产生的倍频光避开基频光的干扰,得到纯正的倍频光。

表1 Gosper 分形超晶格结构晶体中的非共线准相位匹配倍频Table 1 Noncollinear quasi-phase matched frequency doubling in Gosper fractal superlattice crystal

图4 Gosper 分形结构的非共线准相位匹配示意图Fig.4 Schematic diagram of noncollinear quasi-phase matched processes in the reciprocal space of Gosper fractal structure
三次谐波的转换效率和二次谐波的强度有关,根据准相位匹配谐频过程中能量守恒和动量守恒,在非共线准相位匹配过程中,可得
式中,λ为入射基波波长,|Gm,n|为倒格矢的大小,θ为入射波矢与倒格矢之间的夹角。基频光的入射方向与非共线准相位匹配倍频一致,经过0.419 μm-1、0.838 μm-1、1.257 μm-1倒格矢相位补偿,可得到基频波波长为2.134 μm、1.664 μm、1.473 μm 的三次谐波输出,三次谐波的波长分别为711.3 nm、554.7 nm、491 nm,其偏离角(三次谐波与基频波之间的夹角)分别为0.53º、0.91º、1.28º。
2.2 Z 分形超晶格结构
图5(a)为Z 分形超晶格结构的模拟衍射图,从图中可以看出,衍射点关于原点对称,分布在XOY平面的二、四象限。这主要是因为分形经过二维傅里叶变换之后,倒空间的点阵分布与正空间的结构是垂直关系。在Z 分形超晶格结构的正空间中,存在很多倾斜角度不唯一的左倾斜线段(“/”)空间结构,经过傅里叶变换后,在倒空间中形成了与之垂直的衍射斑点。图5(b)为倒空间中不同波长的准相位匹配倍频示意图,从图中可以看出,Z 分形超晶格结构的倒格矢分布比较丰富密集,例如:两个相邻红色圆圈内的衍射亮点之间分布着二等分点;倒格矢G0,2与G-1,2之间、G-1,2与G-2,2之间存在次亮衍射斑点,这为实现频率连续转换提供了前提条件。

图5 Z 分形超晶格结构衍射图Fig.5 Diffraction pattern of Z fractal superlattice structure
如图5(b)所示,红色圆圈内衍射亮点到中心点的距离分别为1.11 cm,2.25 cm,3.34 cm,误差在5%以内,计算可得倒格矢的大小分别为0.443 μm-1、0.898 μm-1、1.333 μm-1。在共线准相位匹配的条件下,可实现基频波长为1.372 μm、1.074 μm、950.5 nm 的倍频光输出。
在Z 分形超晶格结构中,基频光沿Y方向入射,在共线准相位匹配的条件下,通过倒格矢|G0,2|=0.399 μm-1可实现入射波长为1.430 μm 的倍频输出,在非共线准相位匹配的条件下,充分利用了横向高阶倒格矢|G±1,2|=0.438 9 μm-1、|G±2,2|=0.558 6 μm-1、|G±3,2|=0.758 1 μm-1、|G±4,2|=0.978 0 μm-1,实现了入射基波波长分别为1.429 μm、1.425 μm、1.415 μm、1.402 μm 的倍频输出。值得注意的是,在倒格矢G0,2和G±1,2的相位补偿下,可实现的入射波长相差仅有1nm,对连续可谐调波长的频率转换的发展具有重要的意义。
本文在二维Z 分形超晶格结构的基础上,对三维Z 分形超晶格结构进行设计。以二阶三维Z 分形超晶格结构为例进行描述,如图6(a)所示,其空间结构的尺寸大小与二维Z 分形超晶格结构相同,为了使三维结构在YOZ、XOY平面上投影结构更加清楚,去除了前后“Z”首尾相连的空间结构,如图6(b)所示,图中编号与三维相对应,需要注意的是,黑色圆圈处的拐角是图(a)中的虚线圆圈部分投影所形成的。在XOY平面上的投影上还存在着10.32 μm 空间尺寸大小,以及倾斜角度不唯一的右倾斜空间结构(“”),根据二维Z 分形超晶格结构的衍射实验可知,其经过傅里叶变换之后,在倒空间中会形成与之垂直的衍射斑点,该衍射斑点主要存在于一、三象限,这意味着其具有和二维空间相似的倒空间结构。

图6 三维Z 分形超晶格结构Fig.6 Three-dimensional Z fractal superlattice structure
此外,本文还为制备三维Z 分形超晶格结构晶体提供了数据支持。使用飞秒激光直写技术在制备三维Z 分形非线性光子晶体的实验过程中,激光光束经过物镜聚焦后的焦点位置是确定不变的。将样品放置在三维移动台上,通过电脑程序设置移动台XYZ三轴的移动行程来控制三维移动平台的运动,进而实现样品的三维加工。对于一阶三维Z 分形超晶格结构(在图中编号为0~7)来说,其移动行程初始位置为图中编号为0 的位置,坐标(X,Y,Z)为(0,0,0),以μm 为单位沿Y轴移动至编号1 的位置,坐标为(0,15.75,0),在此基础上,继续根据图中的编号进行位置移动,坐标依次对应为(0,0,-27.28)、(0,15.75,-27.28)、(-13.64,0,0)、(-13.64,15.75,0)、(-13.64,0,-27.28)、(-13.64,15.75,-27.28),依此类推,可完成整个三维Z 分形非线性光子晶体的制备。
与单向一维晶体和平面二维晶体相比,三维晶体具备更为丰富的倒格矢,在这些倒格矢的参与下可以预料到,三维Z 分形光学超晶格中的非线性光学现象会更丰富,可以在可见光波段获得多种颜色倍频光输出。此外,南京大学在三维叉形结构铌酸锂非线性光子晶体中实验证明了,在相同制备方法的情况下,三维二阶极化率的调制可以同时满足非线性波前整形和准相位匹配的要求,在数十微米长的三维非线性光子结构中,其转换效率比二维非线性光子晶体提升了两个数量级[23],因此,在同样的条件下,与二维Z 分形超晶格结构相比,三维Z 分形超晶格中的准相位匹配倍频转换效率预计显著提高。
从理论上来说,超晶格结构越紧密,倒格矢分布就会越丰富,更加有利于准相位匹配。但是,在晶体极化过程中,由于外加电场极化技术具有畴壁自发侧向扩展的局限性,使得超晶格结构间距减小,可能会造成反转畴结构连接在一起。分形超晶格结构在正空间上排列相对稀疏,倒空间分布密集,因此,分形超晶格结构可以在外加电场极化技术中,获得更高效的非线性效应,其优势更多体现在高阶的频率转换上。在探索不同超晶格结构优势的过程中,我们研究小组已成功极化了不同类型的铌酸锂非线性光子晶体,例如H 型分形、谢尔宾斯基分形等,因此,极化Gosper 分形与Z 分形的非线性光子晶体具备可行性。
3 结论
本文设计了Gosper 分形与Z 分形两种超晶格结构非线性光子晶体并进行了衍射实验,以铌酸锂晶体为例理论计算了两种分形超晶格结构可实现的谐波波长。Gosper 分形超晶格结构在共线准相位匹配的条件下,能够产生多个波段的二次谐波;在级联三倍频的过程中,基频光沿六个方向中任意一个衍射亮线入射,经过0.419 μm-1、0.838 μm-1、1.257 μm-1倒格矢相位补偿,能够得到基频波波长为2.134 μm、1.664 μm、1.473 μm 的三次谐波输出;Z 分形超晶格结构的衍射斑点分布集中,倒易矢量分布密集,通过横向高阶倒格矢G0,2G±1,2、G±2,2、G±3,2、G±4,2,可实现入射基波波长为1.430 μm、1.429 μm、1.425 μm、1.415 μm、1.402 μm 的二次谐波转换,最小波长间距为1nm。综上所述,Gosper 分形超晶格结构晶体的优势在于,能够在六个不同方向同时实现相同的多个波段的谐波输出,对多路多向的光集成器件有重要意义;Z 分形光学超晶格结构晶体通过横向高阶准相位匹配更有助于实现准连续波长的输出,提高了准相位匹配的实用性。

