圆偏振涡旋光致非轴向自旋和轨道运动研究

蔡亚楠，严绍辉，张亚楠，柳牧龙，张锐，任文艺，姚保利

（1 西北农林科技大学 理学院，杨凌 712100）

（2 中国科学院西安光学精密机械研究所 瞬态光学与光子国家重点实验室，西安 710119）

0 引言

光与微小物体相互作用时会发生动量传递，从而实现对目标物体的操纵，这种光学操纵技术称为光镊。因其具有非接触、无创等优良特性，被广泛应用于各种微观领域的研究［1-3］。例如，在原子物理领域，光镊可以用来捕获、冷却原子，研究玻色-爱因斯坦凝聚；在分子生物物理领域，可以揭示单个生物大分子的功能特性；在生命科学领域，可以深入研究活体细胞的个体行为，探索生命运动规律。近年来，随着光场调控技术的发展，光镊的功能已不仅仅局限于对微粒进行捕获与移动，还能够实现对捕获对象的旋转，这种手段通常被称为光致旋转（也称光学扳手）。光致旋转丰富了传统光镊的功能，并推动了光镊在胶体物理、微流控、生命科学等领域的应用［4-6］。

光致旋转的本质是光和物质相互作用过程中光学角动量的传递：当紧聚焦的光场与微粒相互作用时，光场携带的光子角动量会传递给微粒使后者获得机械角动量从而发生旋转［7］。光子的角动量可以分为外禀的轨道部分和内禀的自旋部分［8］。其中，轨道部分与光场的涡旋相位直接相关，在与微粒相互作用时可以传递给微粒诱导轨道运动；自旋部分与光场的偏振有关，可以诱导微粒的自旋运动。通常情况下，光子角动量的取向与光轴（光束传播方向）平行，称为轴向角动量。在与微粒相互作用时，这类光场可以诱导粒子围绕光轴方向旋转。近年来，在倏逝场、干涉场和聚焦场等结构光场中均发现了横向自旋角动量［9-14］。不同于轴向角动量，横向自旋角动量可以对微粒施加横向力矩令其围绕垂直光轴的方向转动，能为光致旋转操控提供一个新的旋转自由度，从而有可能实现光学非轴向旋转操控。目前，利用特殊结构光场实现非轴向光致旋转的研究已经相继展开［15-17］。例如，PETER B 等利用特殊定制的偏振波片在聚焦光场中获得了纯横向自旋角动量；HANG LI 等设计了二值光学相位板，用以产生携有横向自旋角动量的聚焦场，计算了聚焦场中角动量密度的分布；RUI Guanghao 等利用偶极子反演法在聚焦结构光场中构建了纯横向自旋角动量以及旋向三维可控的自旋角动量，并模拟了纳米级微粒在光场中的受力［18］。这些研究展示了利用聚焦场实现粒子非轴向旋转操控的可能性，但以理论研究为主，实验研究较少。

近轴近似下，左（右）旋圆偏振光携带轴向自旋角动量ℏ（-ℏ）（平均每光子），一般情况下，很难操控粒子非轴向自旋。然而，在紧聚焦条件下，圆偏振光束的聚焦场中可能存在横向自旋角动量［19-21］，进而诱导非轴向自旋效应。涡旋光束携带轨道角动量，主要用于驱动粒子围绕光轴做轨道运动［22-25］。当涡旋光束为圆偏振态时，会同时携带轨道角动量和自旋角动量，其聚焦场有可能同时驱动粒子做轨道运动和非轴向自旋运动［26］。本文提出利用轨道角动量和自旋角动量方向相同的圆偏振涡旋光束捕获粒子，使其同时实现轨道运动和非轴向自旋。为了理解粒子的旋转特性，首先利用T 矩阵理论计算了聚焦光场施加于捕获粒子的光力和光力矩，分析了粒子旋转的动力学机制。然后，利用全息光镊系统产生圆偏振涡旋光，在实验上同时实现了粒子的轨道运动和非轴向自旋操控。

1 理论研究

1.1 理论模型

为了便于实验研究，本文的研究对象选取微米尺度粒子，采用电磁散射模型中的T 矩阵方法分析光场施加给微粒的光力和光力矩。假设一个半径为a，折射率为n2的球形粒子被紧聚焦的涡旋光场照明，根据电磁散射理论，粒子在光场中受到的光力时间平均值和自旋矩时间平均值分别为［19］

式中，ε1和μ1是粒子周围介质的介电系数和磁导率，为单位张量。E( =Einc+Esca)和H( =Hinc+Hsca)表示总的电场和磁场，其中，Einc和Hinc为照明电场和磁场，Esca和Hsca为散射电场和磁场。在T 矩阵方法中，Einc和Esca用矢量球谐函数展开为

式中，k为光在介质中的波数，（amn，bmn）为入射场的展开系数，（pmn，qmn）为散射场的展开系数，和分别是第一类和第三类矢量球谐函数。（pmn，qmn）和（amn，bmn）由T 矩阵关联，考虑到粒子为球形，T矩阵为对角矩阵，其表达式为

将式（4）和（5）代入积分式（1）和（2）中，则粒子受到的光力和自旋矩的时间平均值均可由系数（amn，bmn）和（pmn，qmn）表示。涡旋光聚焦光斑为空心环形光，当粒子被捕获于环上时，会受到轨道矩的作用。假设粒子被稳定捕获时相对光轴的位置矢量为ro，轨道矩的具体表达式为

根据Debye-Wolf 矢量衍射积分［27-28］，作用在粒子上的光场Einc为

式中，f为物镜的焦距，k为光在聚焦区域的波数，θmax为孔径角，由物镜的数值孔径NA=n1sinθmax决定，k为波矢，θ(0 ≤θ≤θmax)和ϕ(0<ϕ≤2π)为观察点的极角和方位角坐标。积分核A(θ，ϕ)与入射场A0(θ，ϕ)关联，关系式为

式中，(eθ，eϕ)为径向和角向的单位矢量，(A0ρ，A0ϕ)为入射场A0(θ，ϕ)的径向和角向分量。假设入射涡旋光束为均匀振幅分布，则入射场可以写成偏振和相位的乘积形式，即A0(θ，ϕ)=uexp(ilϕ)，l为涡旋光的拓扑荷数，u为偏振矢量，对左旋圆偏振（Left-handed Circularly Polarized，LCP）光，有。

1.2 模拟结果

利用上述理论模型分析粒子在光场中的受力。聚焦浸水物镜的数值孔径NA 设为1.27，周围介质折射率n1为1.33，孔径角θmax=arcsin(1.27/1.33)=72.7°，入射光波长为1 064 nm，功率为100 mW，捕获粒子的折射率n2为1.59+0.003i，半径a为1.5 μm。首先，以左旋圆偏振涡旋光（Left-handed Circularly Polarized Vortex Beam，LCPV）为例，研究粒子在圆偏振涡旋光场中的轨道运动特性。假设粒子的轴向平衡位置位于焦平面，图1（a）给出了拓扑荷数为15 和-15 时，焦平面上聚焦光场强度沿x轴的变化曲线，可以看到，聚焦光斑均为空心环形，但拓扑荷l=15 时，产生的聚焦环半径更大。图1（b）和（c）分别为粒子在聚焦光场中受到的径向力沿x轴和y轴的变化曲线。结合三幅图，发现粒子受到的径向光力消失的位置没有与环形光斑强度最大值的位置重合，而是沿着远离光轴的方向偏移120 nm，这说明粒子在光强最大值附近存在稳定的径向捕获。图2（a）和（b）展示了两种光场中粒子在焦平面上的横向受力分布，绿色箭头的方向和大小分别代表横向光力的方向和大小，可以看到，在平衡位置处存在均匀分布的角向力，说明粒子将绕光轴做轨道运动。需要注意的是，当拓扑荷l=15 时，粒子绕正z轴做顺时针轨道旋转；而当l=-15 时，轨道运动反向。这是因为拓扑荷的符号决定了轨道角动量的方向，图2（a）和（b）是光学轨道角动量向粒子传递的结果。

图1 ±15 阶LCP 涡旋光紧聚焦场的归一化强度和粒子受到的径向力的变化曲线Fig.1 Line scans of the normalized intensity distributions and the radial trapping force for tightly focused LCP vortex fields with topological charge of ±15

图2 粒子在LCP 涡旋光作用下的横向力分布Fig.2 Transverse force distributions experienced by the particle under tightly focused LCP vortex fields

由于捕获粒子是吸收性的，它在做轨道运动的同时还可能发生自旋。表1 定量地给出了粒子被捕获于平衡位置时受到的光力矩。对于轨道矩，这里只关注轴向分量。可以看到，粒子除了受轴向轨道矩和自旋矩作用外，还受横向自旋矩作用。这是因为圆偏振涡旋光在紧聚焦条件下产生了轴向电场分量，其与横向电场分量形成了横向的场自旋［29］。因此，粒子的自旋实际上是偏离光轴某个方向进行的，即存在非轴向自旋。还发现，拓扑荷为15 的左旋圆偏振涡旋光施加给粒子的非轴向横向自旋矩是拓扑荷为-15 光场的5.9 倍。这是因为拓扑荷为-15 的左旋圆偏振涡旋光携带的轨道角动量和自旋角动量方向相反，在与粒子相互作用时发生的轨道-自旋耦合效应会削弱自旋矩［7，30］。上述理论模拟结果表明，轨道角动量和自旋角动量方向相同的圆偏振涡旋光更适合同时驱动粒子做轨道运动和非轴向自旋运动。值得注意的是，当研究对象为更小尺寸的粒子（比如半径为1 μm 的粒子），或捕获光场拓扑荷的绝对值改变（比如+13 和-13 的涡旋光），理论模拟光场施加给粒子的轨道矩和自旋矩的数值会略有差异，但会得到与上述相同的结论。

表1 ±15 阶LCP 涡旋光束中粒子位于平衡位置时受到的轨道矩和自旋矩Table 1 Orbital and spin torques exerted on the particle at the equilibrium position under LCP vortex beams with topological charge of ±15

2 实验研究

2.1 实验装置

利用全息光镊系统开展圆偏振涡旋光束捕获特性的实验研究。具体光路如图3 所示，激光器Laser（λ=1 064 nm，工作功率为1.1 W）发出的线偏振光经透镜f1（焦距10 mm）和透镜f2（焦距250 mm）扩束准直后入射至纯相位型液晶空间光调制器（Spatial Light Modulator，SLM，1 920×1 080 pixels，PLUTO NIR-Ⅱ，德国Holoeye）。通过在SLM 上加载全息图的方式可以调制光束的相位，使其携带+15 或-15 阶涡旋相位。调制后的光束被透镜f3（焦距200 mm）和透镜f4（焦距200 mm）组成的4f系统中继至浸水物镜Objective（100×，NA1.27，日本Nikon）的后焦面，再经物镜聚焦后形成紧聚焦场用以捕获粒子。物镜和透镜f4之间放置有四分之一波片（Quarter Wave Plate，QWP），可以将入射线偏振光转换成左旋圆偏振光。包含捕获粒子的样品Sample 被LED 灯照明，其图像被聚焦物镜收集，再经透镜f5成像于CCD 相机（DCC3240M，Thorlabs Inc.，USA）上，记录粒子动态捕获过程。上文的理论模拟中，使用球形粒子作为研究模型，球对称的特点导致它的自旋运动很难在实验上被观察到。参考文献［31，32］，本文选取不规则的碳酸钙粒子作为捕获对象以便能直接观察到粒子的轨道运动和自旋运动。

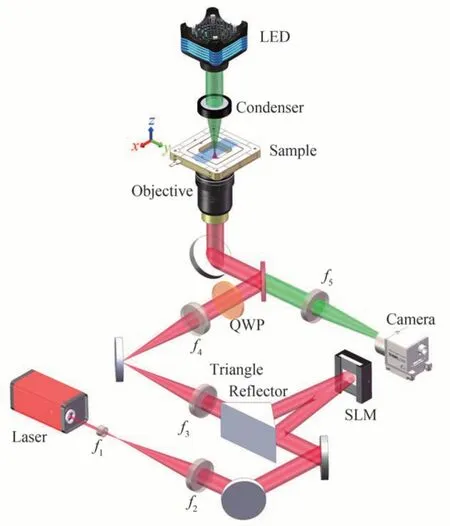
图3 全息光镊系统的光路示意图Fig.3 Schematic diagram of holographic optical tweezer system

2.2 实验结果与讨论

图4（a）～（d）为不规则粒子（尺寸约为3 μm×1.5 μm×2 μm）在拓扑荷为-15 的左旋圆偏振涡旋光聚焦场中光致旋转过程的视频截图。如图4所示，白线描绘了粒子的圆周运动轨道，箭头表示粒子轨道运动的方向，提示粒子在做逆时针轨道运动。粒子在圆形轨道的不同位置时，其长轴方向始终与轨道半径方向垂直，未发现粒子的非轴向自旋运动。正如前文模拟结果提示，当入射光的轨道角动量和自旋角动量方向相反时，粒子受到的非轴向自旋矩很小，且受液体的粘滞力和其他阻力的影响，实验中很难实现粒子的非轴向自旋操纵。虽然提高照明激光的功率可以增大粒子受到的非轴向自旋矩，但这种方法导致的热效应会严重干扰粒子的稳定捕获。

图4 碳酸钙微粒在拓扑荷数为-15 的紧聚焦LCP 涡旋光场中的光致旋转过程Fig.4 Rotating of calcium carbonate particle in the tightly focused LCP vortex beam with topological charge of -15

改变入射光的拓扑荷为+15，观察同一粒子的旋转过程。如图5（a）～（d）所示，粒子在拓扑荷为+15 的LCP 涡旋光场中的光致旋转过程与在拓扑荷为-15 的光场中的情况有差异。首先，可以看到粒子在做顺时针轨道运动，这是因为当涡旋光束的拓扑荷数由-15 调控为+15 后，光束携带的轨道角动量的方向发生了变化，其诱导产生的轨道运动也随之发生改变，轨道运动由逆时针方向变为顺时针方向。视频截图中还可以明显看到，除了轨道运动，粒子同时还在做自旋运动。这是因为，当光场的轨道角动量和自旋角动量方向相同时，粒子受到的横向自旋矩比方向相反时大，从而更容易诱导粒子发生非轴向自旋。为了方便观察粒子的非轴向自旋现象，选取不规则粒子的一处明显特征，对该特征使用黄色圆点标记。在4.29 s 到5.83 s 过程中，黄色圆点标记的特征在围绕微粒自身某点做自旋运动，不同时刻呈现的清晰度不一样。在5.67 s 时刻，黄色标记特征位于轨迹外，在5.83 s 时刻，位于轨迹内，结合整个运动过程可知，微粒自旋运动是围绕某一偏离光轴的方向进行的，即粒子在做非轴向自旋运动，这是横向自旋矩和轴向自旋矩共同作用的结果。

图5 碳酸钙微粒在拓扑荷数为15 的紧聚焦LCP 涡旋光场中的光致旋转过程Fig.5 Rotating of calcium carbonate particle in the tightly focused LCP vortex beam with topological charge of 15

3 结论

本文研究了微米尺度的吸收型粒子在圆偏振涡旋光聚焦场中的动力学特性。数值研究结果表明，粒子被捕获于光强最大值附近围绕光轴做轨道运动的同时，还会受到非轴向自旋矩的作用，该自旋矩与光场携带的角动量的方向有关。当光场的轨道角动量和自旋角动量方向相同时，自旋矩的数值相比反向时更大，从而更易于驱动粒子非轴向自旋。实验上，利用全息光镊系统，捕获并观察不规则碳酸钙微粒在光场中的动态运动过程，初步证实了粒子可以同时做轨道运动和非轴向自旋运动的可能性。本文实现了利用轨道角动量和自旋角动量方向相同的圆偏振涡旋光同时实现粒子的轨道运动和非轴向自旋操纵，对光致旋转的相关应用具有指导意义。