基于COMSOL的中央厨房餐品微波加热包装仿真研究

梁怡良,王利强,2*,张新昌

1(江南大学 机械工程学院,江苏 无锡,214122)2(江苏省食品先进制造装备技术重点实验室,江苏 无锡,214122)

近年来,外卖餐品出餐效率低、密封性差等问题常常被点餐者所诟病,加之新冠疫情的出现,使餐品在安全卫生方面有了更高的要求[1]。而冷冻技术的升级逐渐将大众的眼光聚焦在规模化生产的中央厨房餐品上[2-3],以便当、预制菜等3R食品(ready to cook,ready to heat,ready to eat)为代表的中央厨房餐品的市场份额越来越大[4]。而向来以加热速度快、操作便捷著称的微波加热方式受到用餐者广泛的喜爱,餐品针对性的微波加热技术也随之成为学术界和工业界关注的热点。

朱勇[5]利用COMSOL模拟微波炉加热方便米饭的过程,探究金属化包装贴膜对米饭温度分布均匀性的影响。CHEN等[6]利用COMSOL多物理场耦合对微波加热土豆的过程进行仿真模拟,分析气体扩散系数、渗透率、蒸发速率等参数对微波加热的影响,模型预测的结果与观测结果非常吻合。SALVI等[7]采用多物理场中电磁场、气流场和传热的耦合方法,利用COMSOL建立了连续流微波加热过程中流体温度场的数值模型,模型数值与实验的平均温度基本保持一致。PITCHAI等[8]用COMSOL模拟微波加热冷冻土豆泥的温度情况,空间表面温度模拟值和试验值拟合较好。

本文以有无包装盖膜的土豆泥餐品为研究对象,土豆泥餐品(含水率70%～80%,孔隙率Φ0.8)参照文献[9]制备,借助COMSOL Multiphysics软件,构建电磁场、传热在内的三维多物理场耦合模型模拟土豆泥的微波加热过程,分析餐品包装内部电场、温度场的变化情况,通过微波加热实验对仿真模型的可靠性进行验证,以便优化模型,进一步完善微波炉用餐品包装的设计。

1 材料与方法

1.1 材料与仪器设备

食品级聚丙烯(PP)餐盒(160 mm×110 mm×50 mm)、聚丙烯(PE)膜,苏州和好塑业有限公司;新鲜土豆,天惠超市;纯净水,娃哈哈集团有限公司;M1-L213B型号微波炉,中国美的公司;V320多功能包装机,苏州德森包装机械有限公司;FLIR T440红外热像仪,前视红外热像系统贸易(上海)有限公司;DS1922温度记录仪,上海沃第森电子科技有限公司。

1.2 实验方法

微波加热有多种频率,其中2.45 GHz是国际规定频率之一,可以避免电子、电器产品间的电磁干扰,保证波形的稳定。家用微波炉的频率为2.45 GHz,在微波加热时,能量转换效率很高,约73%。本文采用实验与数值仿真相结合的方法探究餐品包装对于餐品加热效果的影响,如图1所示。

图1 实验装置与仿真系统示意图

1.2.1 实验方法

将新鲜土豆去皮切丁后,置于锅中煮熟,充分捣碎成均匀泥状,取500 g土豆泥装入PP包装盒中,选取5个特征点,如图2所示,在相应位置布置温度传感器,同时保持土豆泥表面的平整,利用包装机将餐盒封膜后置于4 ℃冷柜中6 h。放入微波炉中加热4 min,读取5个特征点的温度变化曲线,采用均匀系数(covariance of temperature,COVT)来定量评价土豆泥的温度均匀程度[10],其计算如公式(1)所示:

(1)

图2 瞬态测温特征点分布示意图

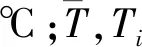
1.2.2 仿真方法

在COMSOL Multiphysics 5.6软件中设置微波炉的功率700 W,模式TE10模,采用矩形波导端口,频率2.45 GHz,设定加热时间240 s。得到土豆泥餐品加热过程中电场和温度的分布图,绘制土豆泥特征点的温度变化曲线。

1.2.3 结果验证方法

为了验证仿真模型的精度,特征点实验与仿真瞬态温度的均方根误差[6](root mean square error, RMSE)的计算如公式(2)所示:

(2)

式中:Ts,仿真模拟温度,℃;Te,实验测量温度,℃;i,数据节点编号;n,数据点总数。

2 微波加热数值模型的构建

微波加热餐品的过程中主要包含4种数学模型:模拟温度变化的传热模型、模拟水分变化的传质模型、谐振腔中场强分布的电磁数学模型和加载样品的电磁场模型[11]。温度是反应餐品微波加热情况的重要指标,本文主要对微波加热餐品温度变化的传热模型进行研究,来预测微波加热的温度分布。

2.1 控制方程及其边界条件

2.1.1 电磁学方程

微波加热餐品时,腔体内部为无源区域(ρ=0),求解麦克斯韦方程组[12]得到微波腔内电磁场分布,如公式(3)所示:

(3)

式中:E,电场强度,V/m;H,磁场强度,A/m;j,电流密度,A/m2;ω,角频率,rad/s;μ,磁导率,H/m;ε0,真空介电常数,F/m;ε′,相对介电常数;ρ,电荷体密度,C/m3。

当电磁波穿过有耗介质时电磁强度减弱,损耗的电磁能作为加热源,其微波耗散能量Qv[13]的计算如公式(4)所示:

Qv=2πfε0ε″E2

(4)

式中:f,微波频率,Hz;ε″,介电损耗因子。

在微波腔中,电场的切向分量Etan在界面处连续,金属波导和炉壁是理想电导体,适用于边界条件[14],如公式(5)所示:

Etan=0

(5)

2.1.2 质量守恒方程

由于土豆泥餐品是土豆泥固相、水和空气的二元混合物,故可以将其看作多孔介质模型进行研究。在微波加热的过程中,土豆泥内水的浓度遵循以下质量守恒方程[6],如公式(6)所示:

(6)

式中:ci(i=w,g),物质(水和气体)的摩尔浓度,mol/m3;Di,物质的扩散系数,m3/s;ui,达西速度,m/s;I,水蒸发速率,kg/(s·m3);Mw,水分子摩尔质量,kg/mol。

利用非平衡蒸发法描述水汽化相变方程[6,15],如公式(7)所示:

(7)

式中:K,水蒸发速率常数,s-1;pv,eq,平衡水蒸汽压,Pa;pv,理想水蒸汽压,Pa;R,理想气体常数。

水气流动是由气压梯度引起的,在多孔介质模型中,流体的动量平衡遵循达西定律[16-17],如公式(8)所示:

(8)

式中:ki,p,渗透率,m2;μi,动力黏度,Pa·s;P,水汽和空气的分压和,Pa。

2.1.3 能量守恒方程

土豆泥餐品加热时,多孔介质模型各相始终保持局部热平衡,能量守恒方程如公式(9)所示[18]:

(9)

式中:Cpi,流体比热容,kJ/(kg·℃);ni,流体通量,kg/(m2·s);keff,有效热导率,W/(m·℃)。

餐品表面与空气发生热量交换,其表面的热量边界条件如公式(10)所示[19]:

(10)

式中:hc,对流换热系数,20 W/(m2·℃);Ta,环境温度,℃。

2.2 几何模型与网格划分

在COMSOL 5.6中,建立21 L微波炉三维模型,模型包括铜质腔体(325 mm×315 mm×202 mm)、金属波导(50 mm×78 mm×18 mm)、玻璃转盘(123.5 mm×6 mm)以及包装盒(160 mm×110 mm×50 mm),土豆泥厚度为30 mm。由于土豆泥是混合物,其比热容和导热系数会随温度变化,为了减少计算量,对模型进行简化处理,利用加权公式计算进行等效替代,输入数值仿真模型的参数,见表1。基于此,构建2种几何模型,如图3所示。

表1 数值仿真模型参数输入值

图3 微波炉加热土豆泥几何模型图

模型一为有包装盖膜餐品,认为模型含20 mm空气顶隙;模型二为无盖膜餐品,不含空气顶隙。网格尺寸会因求解域不同而异,为了提高精度,将模型网格划分为自由四面体单元,其中微波炉腔、玻璃转盘和土豆泥3个区域的网格单元尺寸分别为[8]:2～30 mm,3～6 mm和2～4 mm,创建了360 635个四面体单元,划分结果见图4。采用Nyquist准则来校核最大网格单元尺寸[20],如公式(11)所示:

(11)

图4 微波加热仿真模型的网格划分图

式中:λ,波长,m;c,真空光速,3×108m/s;ε′,相对介电常数;μr,相对磁导率,1 H/m。

2.3 模型假设

为了方便对加热过程研究,对模型做出以下假设。

(1)假设土豆泥和包装质地均匀,初始温度分布均匀,初始温度为4 ℃,温度传导在加热的过程中表现为各向同性,且微波炉内空气的温度保持25 ℃恒定;

(2)假设模拟加热过程中,除了土豆泥及包装以外的所有区域均无固体传热,且包装不发生形变;

(3)假设金属波导和微波炉铜壁可以看作一个理想电导体。

3 结果与讨论

3.1 电场

微波炉谐振腔内电场强度分布也会受土豆泥摆放位置的影响,所以应保持模型一和模型二样品放置位置的一致。微波在炉腔内传播遇到理想电导体边界发生全反射,形成驻波,微波的辐射频率为2.45 GHz,其波长为122.4 mm,驻波为61.2 mm,炉腔长325 mm,除以驻波约为5,在X方向上形成5个电场强峰[22]。图5展示了土豆泥餐品2个模型微波加热时的电场空间分布情况。

a-模型一有盖膜电场分布;b-模型二无盖膜电场分布

在微波加热餐品的过程中,电磁场的分布决定了被加热物料传热场的分布,由图5可知,2个模型电场分布情况大致相同,电场强点和弱点的位置基本一致,区别在于场强的最大值和最小值存在明显差异,说明PE材质包装盖膜的存在会对谐振腔内电场强度产生削弱作用,但不会改变电场强弱点的分布。

3.2 温度场

餐品的加热源主要是微波耗散能量的转换和自身热传导。为了验证数值模型的准确性,分别对有包装盖膜和无包装盖膜餐品进行加热实验,控制实验条件分别与仿真模型一和模型二的一致,实验中受限于土豆泥自身的物理特性,无法将其切开测量切面的温度分布,故本实验测量了样品上表面、下表面、长侧面和短侧面的温度分布,并依照图2收集a、b、c、d和f这5个特征点的温度数据绘制温升曲线。

3.2.1 样品表面温度分布对比

图6-a所示为样品上表面温度分布情况,在加热4 min后,样品上表面边缘产生一周高温带,有盖膜组最高温度实验值为83.0 ℃,无盖膜组最高温度为81.9 ℃,略低于有盖膜组,其主要原因是盖膜的存在使得加热时样品产生的湿热蒸汽难以散失,聚集在样品表面上方的空气顶隙中,从而达到了对样品表面二次加热的效果,而2组的仿真值均达到了85 ℃。中心部位存在圆形的偏高温区,而由中心向四周过渡的区域产生了大面积的低温区,将偏高温区包围。在样品长边方向上,低温区分布在圆形偏高温区两侧。低温区包含了若干个冷点,最低温度仿真值分别达到了25.6 ℃和22.8 ℃,对应的实验值为28.2 ℃和25.1 ℃。图6-b为下表面温度分布情况,同样的,在样品角隅和边缘处产生了高温区,实验最高温度达到了85.5 ℃和84.1 ℃,仿真最高温度均达到了85 ℃,中心部位形成了偏高温区域,但沿长边方向从中心到两端出现了一大一小的低温区,实验最低温度为28.0 ℃和27.1 ℃,仿真最低温度达到了26.3 ℃和24.7 ℃。图6-c和6-d为侧面温度分布情况,可以看出,在样品侧面,高温区依旧是分布在边缘处,靠近中心部位存在着低温区,但此时实验的高低温差要小于仿真的温差,这也是实际操作时热成像采集的滞后带来的影响。

a-样品上表面;b-样品下表面;c-样品长侧面;d-样品短侧面

比较各表面温度分布的实验与仿真结果,发现2组表面最高温度的实验值均低于仿真值,其中的影响因素是在热成像拍照的时间内产生了热量损耗,而最低温度实验值又高于仿真值,原因是在拍照的时间内热传量的继续传递。微波加热方式使得样品存在很大温度分布不均匀性,各表面都有过热区域和过冷区域,受电磁波穿透深度的局限性以及样品介电特性的影响,样品表面边缘部位多是高温区,而低温区存在于中心位置。整体而言,无论包装盒是否带有包装盖膜,样品的表面温度分布情况趋于一致,主要区别在于包装膜的存在对表面温度值的升高起促进作用,而2组样品表面温度分布的实验结果和仿真结果也展现出了很高的一致性,说明了仿真模型具有一定的可靠性。

3.2.2 样品特征点温升曲线对比

单从样品表面的温度分布情况上无法看出餐品内部升温的变化规律,所以需要根据样品内部a、b、c、d、f这5个特征点的瞬态温升曲线进行仿真和实验的对比分析,有盖膜和无盖膜餐品特征点实验与仿真的温升曲线采用Origin 2017绘制,如图7所示。

a-有包装盖膜土豆泥;b-无包装盖膜土豆泥

由图7可知,在微波加热4 min内,有盖膜和无盖膜土豆泥样品各特征点温度持续升高,但升温规律有所差异。在加热初期,靠近表层的特征点a、b、c、d能较好地吸收微波能,升温速度快,中心位置的f点升温慢,温度低。由于实验过程中餐品和包装可能产生热变形导致特征点位置发生偏移,从而引起测量误差,产生加热滞后的现象,表现为加热初期温升较慢。对于有盖膜组,无论仿真还是实验,特征点温度高低的排序为a>c>d>b>f,同样是位于边角,点a和c靠近上表面,受盖膜下方汇集的热气流二次加热的影响,温度值要高于靠近下表面的b点和d点,受电磁场分布的影响,a点和d点更易吸收微波能;反观有盖膜组,无论仿真还是实验,特征点温度高低的排序为d>a>c,b>f,此时没有热气流的影响,加之水分的散失,a点和c点温度值低于d点;位于中心的f点是5个特征点中温升最慢、温度最低的,2组升温情况实验与仿真大致相同,不受包装盖膜的影响。到加热后期,温升的能量来源除了微波能之外,还有局部的热传导,f点更为突出。各特征点的仿真温升速率开始降低,而实验温升速率基本保持不变,这是由于模型的理想化,忽略了比热容随温度的变化,加之样品介电常数实际的变化要复杂得多,从而影响了仿真温度的线性上升。整体来看,2组样品各特征点温升曲线的仿真结果和实验结果大致拟合,可以认为仿真客观地反映了样品微波加热的实际温升情况。

为了进一步探究COMSOL模拟的准确性,利用5个特征点的瞬态温度值计算温度均匀系数,经Origin 2017绘图得到温度均匀系数随时间的变化曲线,如图8所示,COVT值越大,温度分布越不均匀。可以看出,无论有无包装盖膜,样品的仿真和实验温度均匀系数变化趋势大致相同,均表现为先升再降,后在0.2附近趋于平缓稳定。4 min时,有盖膜组的仿真和实验结果略小于无盖膜组,不可否认盖膜对样品加热会产生微小的影响。两组仿真曲线和实验曲线都有2个交点,一方面,有盖膜组在45 s前,COVT仿真值略高于实验值,但差异并不明显,反观无盖膜组,虽然COVT仿真值也高于实验值,但实验COVT曲线发生了明显的滞后,使得实验与仿真COVT曲线在70 s左右才相交,原因可能是无盖膜组在加热实验前15 s内热量散失的速度高于样品微波热的转化速度,使得样品各特征点在低温阶段升温差异不大,而仿真曲线显得更加平滑;另一方面,在加热停止时,2组COVT实验值均稍低于仿真值,也使得仿真模型对样品温度均匀性的预测更加保守。

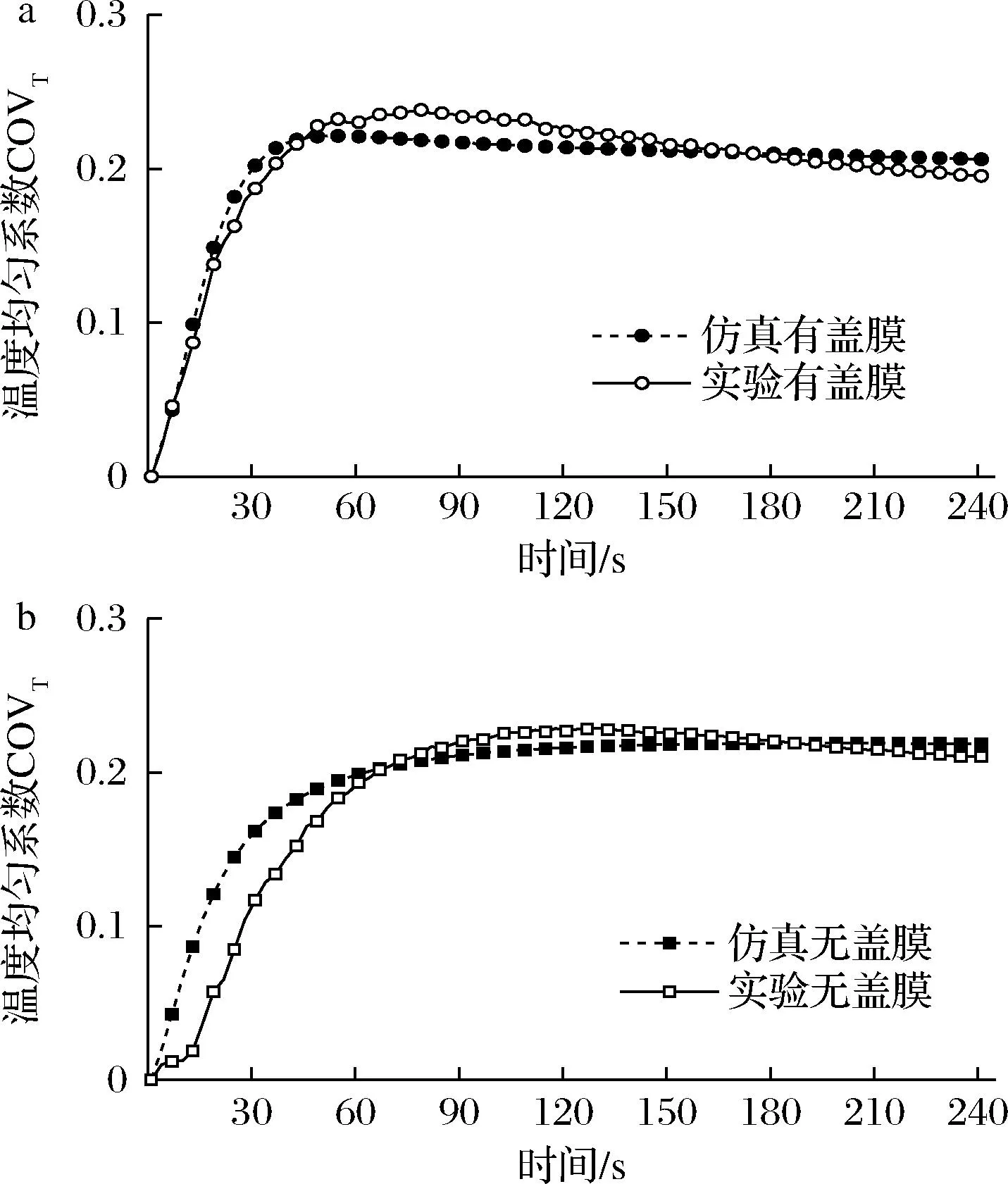
a-有包装盖膜土豆泥;b-无包装盖膜土豆泥

计算样品特征点瞬态温度仿真值与实验值的均方根误差RMSE,来进一步验证模型的精度,如表2所示。在整个加热阶段,有盖膜组土豆泥微波加热特征点温度模拟值和实验值的RMSE平均值为2.955 ℃,温度均匀系数COVT的RMSE值为0.011,无盖膜组的RMSE平均值为2.538 ℃,COVT的RMSE值为0.022,两者拟合较好,表明模型能较好地反映微波加热过程中样品的温度变化趋势,RMSE越小,实验与模拟的差异性越小,当RMSE值小于1时,可认为模型更加精确,具备优化实际产品的要求。

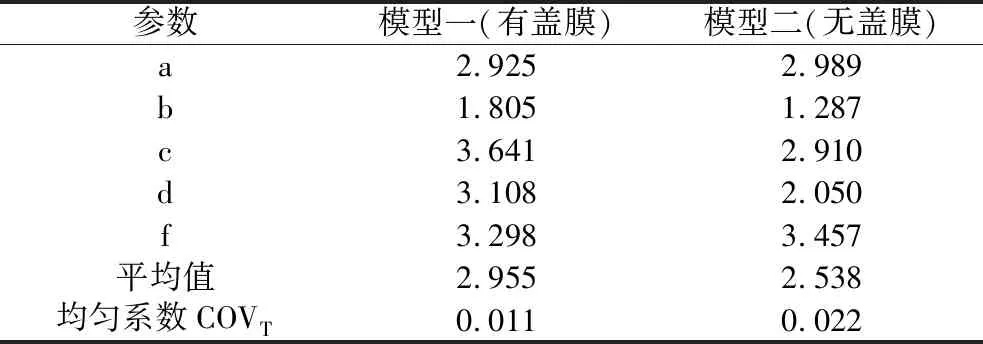
表2 仿真值与实验值的均方根误差RMSE

4 结论

本文利用COMSOL软件模拟土豆泥的微波加热过程,并借助实验验证模型的可靠性,得出如下结论:

(1)模拟值和实验值较为接近,有盖膜组土豆泥微波加热特征点温度模拟值和实验值的RMSE平均值为2.955 ℃,温度均匀系数COVT的RMSE值为0.011(RMSE<1),无盖膜组特征点温度模拟值和实验值的RMSE平均值为2.538 ℃,COVT的RMSE值为0.022(RMSE<1),表明该模型能较好地模拟微波加热过程。

(2)PE包装盖膜的存在不会明显改变电场分布,也不能决定物体加热后的温度分布,无法改善温度分布不均匀的问题,但会影响物料表面的加热效果。

(3)无论有无包装盖膜,样品仿真和实验的温度均匀系数COVT变化趋势大致相同,均表现为先升再降,后在0.2附近趋于稳定,最终有盖膜组COVT的仿真和实验值略小于无盖膜组,不可否认盖膜对样品加热会产生微小的影响。

由于微波能会激发金属表面电子的跃迁产生电火花[23],故可以借助数值仿真模型进行金属优化微波包装[24]的研究,避免实验过程中产生安全隐患。因此,优质的数值模型能为成本高、操作难和危险性大的实验研究提供可靠的仿真代替方案。展望微波加热包装的未来,数值模拟方法将会更加广泛地运用到微波包装的优化研究当中。