基于反馈线性化与非线性扰动补偿的液压型风电机组有功功率控制研究

陈立娟　吴蝶　高伟　魏龙正　曹晟维　艾超　李景彬

摘要：液压型风电机组并网后不能直接发电，需要对有功功率进行控制，而风能具有随机性和波动性，导致该系统具有时变性和非线性，故需解决外部扰动下风机有功功率的精准控制。采用反馈线性化解决液压主传动系统非线性问题，采用非线性扰动观测器快速精准观测外部扰动对系统输出功率的影响，设计了不匹配扰动下的有功功率补偿控制器，精确补偿扰动对系统输出功率的影响，最终得到了液压型风电机组有功功率控制策略。基于30 kV·A液压型风电机组半物理模拟实验平台，使机组输出有功功率能够精准跟随目标转速变化，有功功率绝对误差为±0.05 kW，稳态误差在3%～5%范围内。

关键词：液压型风电机组；有功功率控制；非线性扰动观测器；不匹配扰动

中图分类号：TH137

DOI：10.3969/j.issn.1004-132X.2023.23.013

开放科学（资源服务）标识码（OSID）：

Research on Active Power Control of Hydraulic Wind Turbines Based on

Feedback Linearization and Nonlinear Disturbance Compensation

CHEN Lijuan¹WU Die²GAO Wei³WEI Longzheng³CAO Shengwei³AI Chao³LI Jingbin¹

1.School of Mechanical Engineering，Shihezi University，Shihezi，Xinjiang，200240

2.School of Mechanical Engineering，Nanjing Institute of Technology，Nanjing，211167

3.School of Mechanical Engineering，Yanshan University，Qinhuangdao，Hebei，066004

Abstract：The hydraulic wind turbine could not directly generate electricity after being connected to the grid，it was necessary to control the active power. The wind energy had randomness and volatility. The system had time-varying and nonlinear characteristics，and it was necessary to solve the accurate control of the active power of the fans under external disturbances. The nonlinear problem of the hydraulic main drive system was solved by feedback linearization. The nonlinear disturbance observer was used to quickly and accurately observe the influences of external disturbances on the output power of the system. An active power compensation controller under mismatched disturbances was proposed to accurately compensate the influences of disturbances on the output power of the system，and the active power control strategies of the hydraulic wind turbine were obtained. Based on the semi-physical simulation experimental platform of 30 kV·A hydraulic wind turbine，the output active power of the unit may accurately follow the target speed changes. The absolute error of active power is as ±0.05 kW，and the steady-state errors are within the range of 3%～5%.

Key words：hydraulic wind turbine； active power control； nonlinear disturbance observer； mismatched disturbance

收稿日期：2023-05-30

基金項目：国家自然科学基金（52175240）；河北省杰出青年基金（E2021203020）；中央引导地方科技发展专项资金（ZYYD2022C09）

0 引言

传统型风机以双馈型和直驱型机组为主，其中双馈型风机具有故障率高、齿轮箱体积庞大、维护困难等缺点^［1］；直驱型机组成本较高，同时会给电网带去大量的谐波^［2］，降低发电电能质量^［3］。大型风电机组载荷更加复杂，机组寿命仍需重视，因此，亟需研制一种高寿命、低成本、高性能的风电机组。液压型风电机组创新性地采用液压柔性传动，引入励磁同步发电机，提高了电能质量，延长了机组寿命，采用液压长管路将发电环节落地安装，减小了机舱质量和安装运维成本^［4-5］。

由于风电机组并网之后，发电机转速不会发生变化，但风速的波动、外部环境温度的变化对系统的影响都体现到机组输出功率上，影响有功功率控制的控制精度，因此，学者针对液压型风电机组有功功率的精准控制进行了大量研究^［6-8］。吴超^［9］针对变量泵/马达-液压蓄能器的储能系统，分析了储能装置的能量储放特性，以系统传输功率为控制输出，以风速为输入信号，对储能系统的功率平稳输出作用进行仿真和实验研究，验证该机组在不同风速下控制律的控制效果，提高了风电机组功率输出的稳定性，平滑程度提高了74.6%。WANG 等^［10］提出了一种用于大型海上风电机组的数字静液压传输解决方案，并提出了一种数字静液压传动风电机组在湍流风下的控制策略，研究了马达切换过程中的系统压力控制，以及湍流风作用下机组的动态性能和年发电量，研究結果表明，数字静液压传动的风电机组比静液压风电机组的年发电量提高了1.6%。ESCOBAR-NARANJO等^［11］将极值寻求控制方法扩展应用到静液压传动风力发电机组中，研究了机组在稳定、阶跃和湍流风下极值寻求控制方法的有效性，实现了机组功率控制。ALI等^［12］提出了一种适用于低风速区域的功率优化控制技术，该技术可以进一步提高静压风力发电机组的功率控制能力。

上述针对液压型风电机组有功功率控制的研究为本文液压型风电机组有功功率精准控制的研究提供了一定的方向性。由于液压型风电机组并网后，内外扰动对系统的影响直接反应到有功功率上，因此，亟需采用控制方法精确地补偿不同扰动对有功功率控制的影响，进一步提高有功功率的控制精度。反馈线性化控制（FLC）主要用于消除非线性系统的非线性项，不过对于具有不匹配的不确定性系统，传统的反馈线性化控制系统存在一定弊端，无法使失配且不确定的系统的状态到达期望的平衡点，因此需要推导出新的控制律^［13-15］。同时，有学者通过开发基于干扰观测器的控制算法来抵消系统中不确定项，主要思想是将所有不确定性合并为一项解决扰动问题^［16］。液压型风机属于典型的强耦合、非线性系统，因此依赖传统模型局部线性化控制难以实现精准控制。本文提出了一种基于反馈线性化与非线性扰动观测的液压型风电机组有功功率双变量控制方法，采用反馈线性化方法解决系统相乘非线性的问题，结合非线性扰动观测器解决参数时变以及外界扰动等问题，并将其应用于补偿控制，消除扰动对跟踪性能的影响。

1 液压型风电机组模型建立

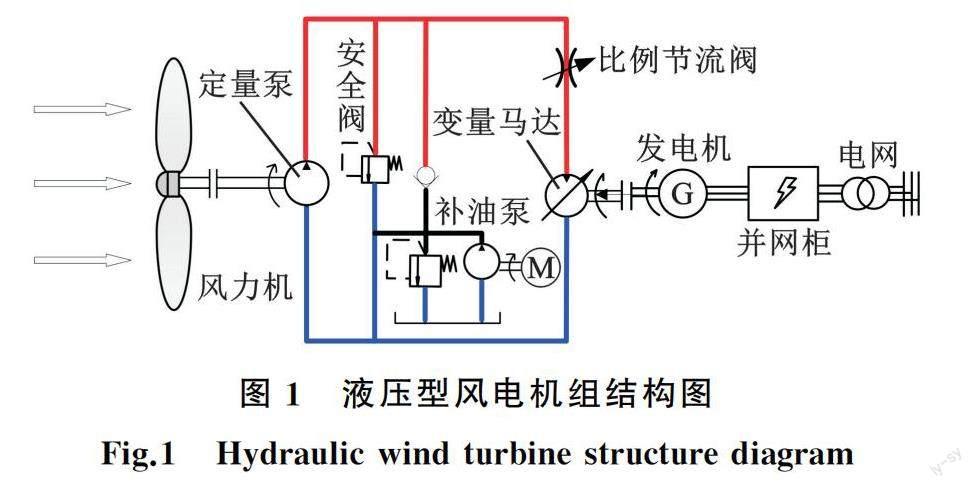
本文所研究的液压型风电机组结构如图1所示，主传动系统为定量泵-变量马达系统，定量泵与风力机相连，变量马达与同步发电机相连，风力机旋转使得泵出口高压油到马达入口驱动其带动同步发电机实现风力发电机组并网，并网后向电网输入有功功率^［17-18］，补油泵主要作用是给定量泵-变量马达闭式液压调速回路补油。

（1）液压泵数学模型。液压泵在风力机作用下输出高压油，流量连续性方程为

式中，q_p为泵的流量；D_p为泵的排量；n_p为泵的转速；C_tp为泵的泄漏系数；p_h1为泵进出口的压力差。

液压泵的力矩平衡方程为

式中，T_w为风力机输出转矩；T_p为泵负载力矩；J_p为泵转动惯量；B_p为泵的阻尼系数；θ_p为泵转角；G_p为泵负载弹簧刚度。

泵输出端刚度很大，由上述分析可得到泵的状态方程为

式中，η_mp为定量泵机械效率。

（2）比例节流阀数学模型。比例节流阀在泵与马达之间，起节流调速作用，其阀芯位移方程为

式中，x_v为节流阀开口大小（0～1）；K为比例系数；U_E为电压信号。

比例节流阀的流量方程可表示为

式中，q_b为比例节流阀流量；p_h2为比例节流阀出口压力；p_L为节流阀压降；K_q为节流阀的流量系数；C_d为节流口的流量系数；ρ为液压油密度；W为节流口的面积梯度。

（3）马达数学模型。马达流量方程为

式中，q_m为马达的流量；C_tm为马达的泄漏系数；K_m为变量马达排量系数；γ为变量马达摆角；n_m为马达的转速。

马达力矩平衡方程为

式中，T_m为马达输出转矩；T_e为马达的负载力矩；B_m为马达的阻尼系数；J_m为马达的转动惯量；G_m为马达负载弹簧刚度；θ_m为马达转角。

考虑到马达输出端刚度很大，由上述分析可得变量马达的动态方程为

式中，η_mm为变量马达机械效率。

（4）液压系统输出数学模型。液压系统的输出转矩为

液压系统的输出功率为

风力发电机组并网后，发电机（马达）转速受电网牵制稳定于同步转速。此时，液压系统输出功率取决于系统压力和变量马达摆角大小。

根据式（3）、式（5）和式（8）可得状态空间表达式。液压系统输出转矩以及功率主要取决于系统中马达入口压力和马达转速与摆角，其中，马达转速与入口压力可分别通过转矩转速及压力传感器实时采集监测，在系统并网后，马达转速根据电网频率要求，稳定于该转速，此时，马达入口压力与摆角是影响系统输出转矩与输出功率的主要因素。

可得液压主传动系统的数学模型为

式中，β_e为油液弹性模量；V₁为定量泵与比例节流阀之间的高压管路容积；V₂为比例节流阀与变量马达之间的高压管路容积。

液压型风电机组并网之后，变量马达转速和发电机转速为定值，即n_m=n_e=1500 r/min，且比例节流阀完全打开，因此，系统的状态空间模型可写为

式中，n_md为变量马达功频转速，n_md=1500 r/min；V₀为定量泵与变量马达之间的管路容积，V₀=V₁+V₂。

根据式（12），系统存在耦合项和不确定项，会影响系统的控制精度。

2 不匹配扰动下的有功功率控制

机组并网之后，液压主传动系统直接解耦，因此，机组有功功率控制可通过液压主传动系统有功功率闭环控制来实现。本文采用反馈线性化方法分别结合液压主传动系统的高压压力、定量泵转速来实现有功功率的闭环控制。针对参数的时变性和外界扰动对有功功率控制精度的影响，采用扰动观测器对扰动量进行观测，并基于不匹配扰动补偿控制器得到扰动的补偿量。最后，将闭环控制量与扰动补偿量进行线性叠加，动态调整变量马达摆角和比例节流阀的控制电压，以实现液压型风电机组有功功率的高精度控制。基于不匹配扰动的机组有功功率控制框图见图2。

2.1 液压主传动系统有功功率控制策略

令x₁=n_p，x₂=p_h，u=γ，即有

将式（13）写成仿射非线性形式，其中，在不考虑扰动的情况下，f（x）和g（x）的表达式如下：

2.1.1 反馈线性化控制律

（1）系统控制输出。以捕获的功率为控制输出，即控制输出可表示为

（2）系统相对阶r求解如下：

因此，系统的相对阶r=1。如果系统的所有状态存在L_gL_fh（x）=0，必须经过多次微分得

（3）反馈线性化控制律。结合（14）、式（15）和式（17）可得

式中，u_fb为反馈线性化控制变量。

由式（15）和（16）可知，L_fh（x）可表示为

由式（16）可知，液压主传动系统控制变量状态为

状态A（x）的倒数为

跟踪偏差可表示为

式中，y_d为液压主传动系统的目标功率；y为液压主传动系统采集的功率。

跟踪偏差的一阶微分形式可写为^［19］

等效控制律v₁可定义为

为保障系统稳定性，令

通过上述计算，反馈线性化的控制律可设计为

因此，在不考虑扰动情况下，将式（20）、式（14）、式（25）代入式（26）中，得反馈线性化控制律为

2.1.2 扰动补偿控制律

考虑到包含扰动的非线性系统，式（13）所示的系统可以表示为^［20］

式中，d为外源系统产生的扰动矩阵；u_d为系统扰动补偿控制变量；g_d（x）为单位矩阵。

为了降低式（28）所示的扰动问题，提出了一种有功功率控制系统扰动观测器^［21］，具体如下：

式中，p（x）为非线性扰动观测器增益；N（x）为设计的矩阵函数；M为非线性状态观测器状态；d^为扰动估计值。

矩阵函数N（x）可设计为

式中，k_p为矩阵函数N（x）增益系数，且为正值。

因此，非线性扰动观测器增益p（x）可以表示为

因此，扰动观測量为

式中，M₁为非线性状态观测器状态1；M₂为非线性状态观测器状态2。

若设计合理的矩阵函数N（x），使d^接近d，则需要式（34）成立：

式中，e_d为扰动估计值与扰动值的偏差，e_d=d^－d。

当t→∞，d· 0，则液压主传动系统有功功率控制扰动补偿控制系统全局稳定，任何N（x）可以被选择来保证估计误差的渐近收敛性。

系统观测扰动的补偿量为

其中，φ为扰动补偿状态，φ可表示为

式中，φ₁为扰动补偿状态1；φ₂为扰动补偿状态2。

由于该系统只有一个输出，且由式（16）可知，系统的相对阶为1，即r=1，因此，式（36）可写为

式中，g_d1、g_d2分别为单位矩阵g_d的列矩阵。

结合式（15），－L_gd1h（x）和－L_gd2h（x）可表示为

将式（38）代入式（36），扰动补偿状态φ可表示为

因此，最终的扰动补偿控制器为

基于上述分析，得到反馈线性化控制器u_fb和扰动观测器控制律u_d，有功功率非线性扰动系统的控制器可表达为

由式（41）可知，本文所提出的控制器参数主要包括反馈线性化控制参数k₁、矩阵函数N（x）增益系数k_p，控制器参数整定主要考虑控制系统稳定的收敛性和控制精度，其中随着工况的变化会微调控制器参数，具体数值如表1所示。

2.2 有功功率控制器稳定性分析

选择式（42）作为非线性系统（28）的李雅普方程：

则式（42）的微分形式为

由式（24）、式（25）可知，基于反馈线性化的闭环控制偏差一阶微分形式e·_fb可表示为

将式（34）和式（44）代入式（43）可得

其中，k₁>0，k_p>0。

式（45）满足李雅普诺夫稳定性理论，因此，液压主传动系统有功功率控制系统渐近稳定。

3 仿真分析

为验证本文所提控制策略理论分析的有效性，对不同风工况和目标功率下机组有功功率控制效果进行仿真分析，仿真参数如表2所示。

在0 s启动主传动系统有功功率控制策略，150 s时给定液压型风电机组7 m/s-8 m/s的阶跃风速，给定目标功率为2 kW-4 kW。变量马达端无负载扰动下，观察液压主传动系统相关物理量变化情况，并将本文所提出的反馈线性化结合非线性扰动补偿控制方法（FLC+DOB）的控制效果与反馈线性化含积分控制方法（FLC含积分）的控制效果进行对比，具体如图3所示。

由图3可以看出，本文提出的控制算法的控制效果相比于反馈线性化控制效果，定量泵转速增大了10 r/min左右，高压压力减小了0.06 MPa，风电机组捕获的风功率稳态误差减小了25 W，稳态误差几乎为0，变量马达摆角增大了0.01，变量马达摆角的增大主要用于补偿扰动量的影响。结合功率指令以及变量马达输出功率可知，功率的响应时间以及超调量相对较小，即响应时间缩短了0.8 s，超调量减小了53%，进一步证明了本文所提控制策略的有效性。

为进一步验证本文所提控制策略的控制效果，给定液压型风电机组5 m/s（±0.5 m/s）-7 m/s（±0.5 m/s）的阶跃波动风速，且阶跃时间为150 s，目标功率为2 kW。观察液压主传动系统定量泵转速、高壓压力、有功功率以及变量马达摆角等物理量在本文所提控制策略下的响应情况，结果如图4所示。

由图4可知，与反馈线性化控制相比，采用本文所提控制策略，定量泵转速相比增大17 r/min，高压压力相对减小0.18 MPa，风电机组捕获的风功率稳态误差几乎为0，变量马达摆角增大0.02，变量马达摆角的增大主要用于补偿扰动量的影响。结合功率指令以及变量马达输出功率可知，有功功率的调整时间以及超调量相对较小，调整时间缩短了101.44 s，超调量减小了53%，进一步验证了本文所提非线性观测器的快速性和准确性以及控制策略的有效性。

4 实验研究

基于图5所示的液压型风电机组原理搭建本文的实验平台，由风电机组模拟系统、液压主传动与并网发电系统、数据采集与监控系统以及控制系统组成。实验平台主要参数如表2所示。

风电机组模拟系统采用伺服电机输出转速和转矩驱动定量泵转动模拟风电机组特性，控制系统通过采集系统的相关物理量来实现并网转速、有功功率与功率追踪等高精度控制，液压型风电机组状态监测平台实时观测和采集整机状态信息。

发电机并入电网之后并不能直接发电，需要对机组的有功功率进行控制。为验证本文所提有功功率控制策略的有效性，在恒定定量泵转速、阶跃定量泵转速两种工况下开展实验研究与验证。

给定定量泵1500 r/min的恒定转速，在目标功率1.5 kW的工况下，系统各物理量状态变化如图6所示。

由图6可知，在恒定定量泵转速指令和目标功率需求下，发电功率、定量泵输入功率和发电效率基本随着目标功率的变化而变化，定量泵输入功率基本稳定在5.98 kW，发电效率基本稳定在0.25，液压系统效率基本稳定在0.75，相对目标功率有功功率的响应时间最大值为20 s，最大绝对误差为±0.05 kW，稳态误差为3.33%。有功功率在定量泵转速切换瞬间发生波动但20 s内会重新稳定在1.5 kW目标功率，有功功率虽然会受定量泵转速影响发生波动，但很快就会重新稳定在目标功率，具有较强的鲁棒性，验证了本文所提控制策略的有效性。

由图6e和图6f可知，发电系统的无功功率由1.1 kW减小到-0.4 kW，且只在有功功率跌落瞬间，无功功率为负值，主要原因是，为电源电压与电网负载电压之间存在相位差，电网就需要吸收一定量的无功功率来维持运行的稳定性。功率因数由0.85变化到1，表征有功功率对视在功率的比值，说明有功功率比重较大。

给定定量泵1570 r/min-1600 r/min的阶跃转速模拟风速突变的工况，在目标功率为1.5 kW的工况下，观察系统的有功功率、系统捕获功率、系统的传输效率和发电效率、无功功率和功率因数等物理量状态变化，结果如图7所示。

由图7可知，在定量泵转速1570 r/min-1600 r/min的阶跃指令和1.5 kW目标功率工况下，发电功率、定量泵输入功率、发电效率基本没有变化，发电功率基本稳定在1.5 kW，相比目标功率，绝对误差为±0.06 kW，稳态误差为4%，在3%～5%范围内。定量泵输入功率基本稳定在6 kW，发电效率基本稳定在0.25，液压系统效率基本稳定在0.69，说明在本文所提出的控制策略下，系统的发电功率不跟随定量泵转速而发生波动或产生变化，只跟随目标功率变化，具有较强的鲁棒性。

由图7e和图7f可知，发电系统的无功功率由-0.58 kW变化到1.78 kW，功率因数由0.48变化到1，主要原因是，为保障发电机输出的有功功率满足目标功率和电网供需侧的需求，发电机在定量泵转速变化瞬间从电网短暂地吸收了无功功率。

对比分析风电组机阶跃负载功率下有功功率控制效果与阶跃定量泵转速下有功功率控制效果，实验结果表明：在阶跃负载有功功率控制目标工况下，机组输出有功功率能够精准跟随目标转速变化，有功功率绝对误差为±0.05 kW，功率指令切换过程有功功率比较平稳无明显波动。在定量泵转速阶跃指令和恒定目标功率工况下，虽在转速阶跃点有功功率会发生波动，但有功功率很快就会重新稳定在目标功率，具有很强的鲁棒性，验证了本文并网发电有功功率控制策略的有效性。

5 结论

（1）以液压型风电机组为研究对象，基于液压型风电机组有功功率精准控制需求，采用理论分析和实验研究的方法，建立并网后液压风机模型，分析机组输出功率的影响，并提出了考虑不匹配扰动的液压型风电机组功率精准控制策略。基于并网后液压型风电机组系统状态空间模型，得到液压主传动系统非线性项和扰动项。设计了有功功率控制系统非线性扰动观测器，将反馈线性化方法和不匹配扰动状态观测补偿方法相结合，提出液压型风电机组有功功率精准控制策略，实现了有功功率的精准控制。

（2）开展了液压型风电机组有功功率半物理模拟实验研究。基于30 kV·A液压型风电机组半物理模拟实验平台，验证在时变液压参数和负载扰动下，液压型风电机组有功功率控制效果。机组输出有功功率能够精准跟随目标转速变化，有功功率绝对误差为±0.05 kW，稳态误差在3%～5%范围内。

随着风电机组在电网中的占比不断提高，电力系统不仅需要风电机组输出功率平稳，而且需要风电机组输出的有功功率能够匹配电网负荷功率的需求，今后将进一步针对网侧负荷的需求如何主动调配机组输出功率开展研究。

参考文献：

［1］HAN Bin，GAO Hongyan. Linear Parameter-varying Model Predictive Control for Hydraulic Wind Turbine［J］. Actuators，2022，11（10）：1-17.

［2］CHEN Lijuan，ZHENG Pengfei，GAO Wei，et al. Frequency Modulation Control of Hydraulic Wind Turbines Based on Ocean Used Wind Turbines and Energy Storage［J］. Energies，2022，15（11）：1-33.

［3］AI Chao，ZHANG Lin，GAO Wei，et al. A Review of Energy Storage Technologies in Hydraulic Wind Turbines［J］. Energy Conversion and Management，2022，264：1-20.

［4］AI Chao，ZHOU Guangling，GAO Wei，et al. Research on Quasi-synchronous Grid-connected Control of Hydraulic Wind Turbine［J］. IEEE Access，2020，8：1-20.

［5］MULDERS S P，DIEPEVEEN N F B，van WINGERDEN J W. Extremum Seeking Control for Optimization of a Feed-forward Pelton Turbine Speed Controller in a Fixed-displacement Hydraulic Wind Turbine Concept［J］. Journal of Physics：Conference Series，2019，1222（1）：1-10.

［6］MALIK M Z，BALOCH M H，GUL M，et al. A Research on Conventional and Modern Algorithms for Maximum Power Extraction from Wind Energy Conversion System：a Review［J］. Environmental Science and Pollution Research，2021，28（5）：5020-5035.

［7］ABDULLAH M A，YATIM A，TAN C W，et al. A Review of Maximum Power Point Tracking Algorithms for Wind Energy Systems［J］. Renewable & Sustainable Energy Reviews，2012，16（5）：3220-3227.

［8］KUMAR M，SARAVANAN B，SANJEEVIKUMAR P，et al. A Review on Control Techniques and Methodologies for Maximum Power Extraction from Wind Energy Systems［J］. IET Renewable Power Generation，2018，12（14）：1609-1622.

［9］吳超. 储能式液压型风力发电机组平稳输出控制［D］. 秦皇岛：燕山大学，2019.

WU Chao. Smooth Output Control of Energy Storage Hydraulic Wind Turbine［D］. Qinhuangdao：Yanshan University，2019.

［10］WANG F，CHEN J C，CHENG M，et al. A Novel Hydraulic Transmission Solution to Large Offshore Wind Turbine：Design and Control Strategy［J］. Ocean Engineering，2022，255：111-121.

［11］ESCOBAR-NARANJO D，MOHANTY B，STELSON K A. Experimental Validation of Extremum Seeking Control for a Midsize Hydrostatic Transmission Wind Turbine［C］∥Fluid Power Systems Technology. Bath，2022：1-13.

［12］ALI A E，DELDAR M，ANWAR S. Optimal Control of Hydrostatic Drive Wind Turbines for Improved Power Output in Low Wind-speed Regions［J］. Energies，2021，14（16）：5001.

［13］KUMAR D，MAHATO A C，PRAKASH O，et al. Priority Flow Divider Valve and Its Dynamic Analysis Using Various Hydraulic Drive Systems：a Bond Graph Approach［J］. Mechanical Sciences，2022，13（1）：459-472.

［14］ZHANG J R，CHEN W T，AI C，et al. Research on High Precision Control of Maximum Power Point Tracking for Offshore Hydraulic Wind Turbine［C］∥Fluid Power Systems Technology. American Society of Mechanical Engineers，2022，86335：1-30.

［15］AI C，BAI W，ZHANG T，et al. Research on the Key Problems of MPPT Strategy Based on Active Power Control of Hydraulic Wind Turbines［J］. Journal of Renewable and Sustainable Energy，2019，11（1）：1-8.

［16］YARMOHAMMADIA M J，TAGHIZADEHA M，SADEGHZADEHB A. Assessing Short-term Storage Effects on Hydrostatic Wind Turbine in Presence of Turbulent Wind［J］. Amirkabir Journal of Mechanical Engineering，2021，53（6）：3431-3444.

［17］艾超，张亚滨，陈汉超，等. 液压型风力发电机组低电压穿越分层控制研究［J］. 机械工程学报，2018，54（20）：96-105.

AI Chao，ZHANG Yabin，CHEN Hanchao，et al. Research on Hierarchical Control of Low Voltage Ride through of Hydraulic Wind Turbine［J］. Journal of Mechanical Engineering，2018，54（20）：96-105.

［18］陈革新，艾超，张亮，等. 液壓型风力发电机组低电压运行特性分析［J］. 液压与气动，2017（7）：33-42.

CHEN Gexin，AI Chao，ZHANG Liang，et al. Analysis of Low Voltage Operation Characteristics of Hydraulic Wind Turbine［J］. Hydraulic and Pneumatic，2017（7）：33-42.

［19］ZOU Yidong，HU Wenqing，XIAO Zhihuai，et al. Design of Intelligent Nonlinear Robust Controller for Hydro-turbine Governing System Based on State-dynamic-measurement Hybrid Feedback Linearization Method［J］. Renewable Energy，2023，204：635-651.

［20］ZHANG Yuchen，MA Mengchen，YANG Xiaoyan，et al. Disturbance-observer-based Fixed-time Control for 6-DOF Spacecraft Rendezvous and Docking Operations under Full-state Constraints［J］. Acta Astronautica，2023，205：225-238.

［21］JOKAR H，VATANKHAH R，MAHZOON M. Active Vibration Control of Horizontal-axis Wind Turbine Blades Using Disturbance Observer-based Boundary Control Approach［J］. Engineering Structures，2023，275：1-14.

（编辑 袁兴玲）

作者简介：陈立娟，女，1989年生，博士研究生。研究方向为流体与传动。E-mail：chenlj@njit.edu.cn。李景彬（通信作者），男，1980年生，教授、博士研究生导师。研究方向为农业机械装备创新与性能设计。E-mail：ljb8095@163.com。