基于闭环辨识模型的永磁同步直线电机分数阶反馈控制方法
钟永彬 高健 冯富原 张揽宇
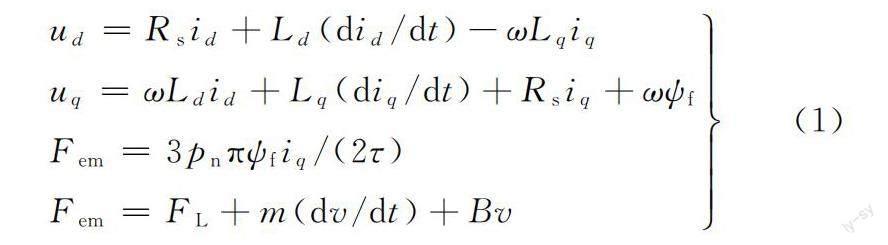
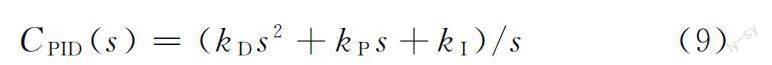

摘要:為了提高永磁同步直线电机(PMLSM)的跟随精度,提出了一种基于闭环辨识模型的分数阶反馈控制方法,通过对反馈控制系统误差幅值特性进行特定分数阶次形式的精准调节来有效抑制PMLSM的跟随误差。该方法推导了PMLSM闭环辨识模型,通过误差幅值特性分析,确定了分数阶超前-滞后补偿器参数选定方法,以实现分数阶反馈控制系统对PMLSM控制频域特性的准确描述,进而提高PMLSM辨识精度及控制性能。采用所提方法在PMLSM龙门运动平台上进行辨识方法和不同运动规划的跟踪实验及圆轨迹运动实验的验证,实验结果表明,该闭环辨识方法能有效抑制外界对辨识信号的干扰,所建立的闭环辨识模型准确性高;相较于PID控制方法,所提分数阶反馈控制方法能够大幅减小PMLSM跟随误差,对于不同运动规划,跟随误差的均方根误差值减小至少82.47%,验证了所提方法可有效提高PMLSM跟踪精度。
关键词:永磁同步直线电机;跟随精度;闭环辨识;分数阶反馈控制;频域特性调节
中图分类号:TP271
DOI:10.3969/j.issn.1004-132X.2023.23.001
开放科学(资源服务)标识码(OSID):
Fractional-order Feedback Control Method for PMLSMs Based on
Closed-loop Identification Model
ZHONG Yongbin1GAO Jian1,2FENG Fuyuan1ZHANG Lanyu1,2
1.State Key Laboratory of Precision Electronic Manufacturing Technology and Equipment,
Guangdong University of Technology,Guangzhou,510006
2.Key Laboratory of Intelligent Inspection and Manufacturing IoT of Ministry of Education,
Guangdong University of Technology,Guangzhou,510006
Abstract:In order to improve the tracking accuracy of PMLSMs,a fractional-order feedback control method was proposed based on closed-loop identification model. By precisely adjusting the error amplitude characteristics of the feedback control system in a specific fractional-order form,the following errors of PMLSMs might be effectively suppressed. A closed-loop identification model was derived for the PMLSM and the parameter selection method of the fractional-order lead-lag compensator was determined based on analysis of the error amplitude characteristics. With the properly defined fractional-order parameters,the fractional-order feedback control system might accurately describe the frequency-domain characteristics of the PMLSM,and the identification accuracy and control performance of the PMLSM might thus be improved. The proposed method was experimentally validated on a PMLSM gantry motion platform through identification methods, tracking experiments with different motion planning, and circular trajectory motion experiments. The experiments on system closed-loop identification and motion tracking with different plannings were performed. The experimental results show that the closed-loop identification method may effectively suppress the influences of external interferences on the identification signals,and the closed-loop identification model is accurate for the control system,the proposed fractional-order feedback control method may greatly reduce the tracking errors of the PMLSMs,and compared to the PID control method,the proposed control method may reduce the root mean square error (RMSE) tracking errors by at least 82.47% under different motion scenarios. The experimental results demonstrate the effectiveness of the proposed method in improving the tracking accuracy of PMLSMs.
Key words:permanent magnet linear synchronous motor(PMLSM); tracking accuracy; closed-loop identification; fractional-order feedback control; frequency-domain characteristics adjustment
收稿日期:2022-11-23
基金项目:国家自然科学基金(52075106,U20A6004)
0 引言
随着集成电路制造技术的飞速发展,芯片上可容纳的晶体管数目不断增加,芯片内部空间不断密集化,为了保证芯片制造良品率,集成电路产业对精密电子元件制造和测试设备精度及效率的要求越来越高,于是,具有高功率密度、高效率及出色控制性能的永磁同步直线电机(permanent magnet linear synchronous motor,PMLSM)被广泛应用于集成电路产业设备的研发[1-2]。PMLSM能够直接驱动实现直线运动,相较于旋转电机具备更好的开发应用前景,所以PMLSM常与精密运动平台研究关联在一起[3-5]。
PMLSM结构简单,主要包括由永磁铁组成的初级定子以及由线圈组成的次级动子两个部分。运行过程中,受齿槽力、端部效应及导轨摩擦力等的影响,PMLSM出现的推力波动将导致跟随精度以及稳定性下降。为此,学者们进行了深入的研究,在齿槽力模型分析的基础上,改进PMLSM结构,以减小齿槽力对推力的影响,提高PMLSM推力稳定性和运动精度[6-7]。与此同时,也有学者从改进PMLSM控制系统的角度来提高其运行精度[8-9]。因PMLSM运动受其自身电气特性及结构特性影响比较大,所以,模型控制理论被广泛应用于PMLSM精密运动控制方法研究,如改进电流预测控制方法、磁通量反馈补偿控制方法等[10-12]。从学者的研究结果可以看出,PMLSM模型的准确性在很大程度上决定了控制系统的性能。吴路路等[13]指出,可以通过提高PMLSM模型准确性来实现控制系统性能的提高。由于PMLSM内部元件在工作时的电磁关系存在复杂的耦合现象,且其电气、结构参数无法直接通过测量获得,所以,学者们结合最小二乘法,提出了基于辅助变量的辨识方法[14]、基于改進遗传算法的参数辨识方法[15]、基于机器学习的参数辨识方法[16]等,均在一定程度上提高了参数辨识的准确性以及简便性。然而,由于覆盖全频段的控制信号需要采用扫频信号、M序列信号等才能实现PMLSM的全面辨识,所以其控制信号易受电压干扰、噪声干扰等的影响,容易使辨识信号中的较高频段电流分量产生高频波动,导致辨识信号精度下降[17]。针对这一问题,本文建立带电流环控制的PMLSM闭环辨识模型来实现PMLSM的闭环辨识,减小干扰信号对参数辨识的影响,提高PMLSM辨识的准确性。随着分数阶微积分计算方法的发展,分数阶控制理论得到快速发展,其微分算子阶次可为分数形式这一特点,使其能更准确地表达被控对象控制频域特性,所以,将分数阶控制理论应用于机电伺服控制系统中具备优势[18-19]。
本文提出了基于闭环辨识模型的分数阶反馈控制方法,结合分数阶控制理论和误差幅值特性,提出了分数阶超前-滞后补偿器参数选定方法,实现被控对象所需频域特性的准确表达。
1 永磁同步直线电机闭环辨识建模
由于永磁同步直线电机在UVW坐标系下的数学模型复杂,难以在其基础上寻求很好的控制方法,故本文采用Clarke变换、Park变换将电压从三相静止UVW坐标系变换到两相旋转dq坐标系下进行建模及控制系统设计[20],以实现PMLSM的最佳控制。根据PMLSM的电气特性及动力学特性,得到dq坐标系下的PMLSM数学模型为
式中,ψf=M0If,为转子每极永磁磁链;M0为初级和次级的互感幅值;If为永磁体等效电流;ud、uq分别为d、q轴的控制电压;id、iq分别为d、q轴的控制电流;Fem为电磁推力;Rs为每相绕组电阻;Ld、Lq分别为d、q轴的每相绕组电感;τ为极距;pn为极对数;ω为电角速度;v为次级运动速度;FL为外力;m为运动部分质量;B为黏性摩擦因数。
结合id=0的矢量控制策略,此时,电机的q轴电压量uq满足
将式(2)代入式(1)并做拉氏变换,可以得到PMLSM运动系统从控制电压到速度的传递函数,模型框图见图1中蓝色框,传递函数表达式为
根据式(3),整理可得PMLSM的开环辨识模型传递函数:其中,ai、bi为所需辨识参数。式(4)的分母多项式最高阶次为2,分子多项式最高阶次为1,为二极点单零点模型。辨识模型的建立及阶次确定能够在保证辨识准确性的前提下节省参数辨识时间,参数辨识过程中仅需计算参数ai、bi即可获得完整的PMLSM模型。在此基础上,本文将电流环PI闭环反馈控制器引入到PMLSM建模及参数辨识中,加入电流环后的模型框图见图1。电流环PI闭环反馈控制器的表达式为
其中,kP、kI分别为闭环反馈控制器的增益系数与积分系数。电流环的加入能够保证控制信号的跟随精度,但同时也改变了辨识结构。系统辨识对象从原先的PMLSM系统转变为电流环与PMLSM所组成的整体系统,所以用于参数辨识的模型也将发生改变。为了保证参数辨识的准确性,需要建立带电流环控制的PMLSM闭环系统相应的模型,并计算其准确的传递函数阶次。通过建立PMLSM闭环反馈控制回路框图,推导出PMLSM闭环模型传递函数:
整理可得PMLSM闭环模型传递函数:
其中,分母多项式最高阶次为3,分子多项式最高阶次为2。到此就建立了带电流环控制的PMLSM系统闭环辨识模型。
由于PMLSM一般采用直线光栅尺、激光干涉仪等测量装置获取其位移信息作为闭环反馈信号,所以,建立电压到位移的传递函数模型更加有利于控制系统的设计。根据速度与位移之间的时间积分关系,PMLSM从电压到位移的模型传递函数为
2 基于闭环辨识的分数阶反馈控制方法
在建立PMLSM闭环辨识模型的基础上,本文设计了基于辨识模型的分数阶反馈控制方法,其控制结构如图2所示,图中,R为参考位移,Y为输出位移,u为PID闭环反馈控制器输出电压,uf为经过频域特性补偿后的控制电压。本文所提方法在PID闭环反馈控制器CPID(s)基础上,根据闭环控制系统频域特性,通过分数阶超前-滞后补偿器CF(s)对指定频域范围内幅值特性、相位角度特性进行补偿,提高反馈控制系统对低频信号的响应性能,从而改进PMLSM运动精度。PID闭环反馈控制器可表达为
其中,kD为闭环反馈控制器的微分系数。在频域内,分数阶超前-滞后补偿器可表达为
式中,K、λ、x均为分数阶超前-滞后补偿器参数;α为分数阶超前-滞后补偿器阶次。
分数阶微积分理论的引入使得分数阶超前-滞后补偿器阶次不再局限为整数0、1或2,其取值为(0,2)内的任意实数。分数阶超前-滞后补偿器能够根据被控对象频域特性进行更加准确的幅值特性、相位特性调节,保证控制系统具备优异的响应性能。图3所示为不同阶次以及不同增益常数的超前-滞后补偿器(a)λ=0.8、K=1、x=0.85,不同α取值(b)α=0.7、K=1、x=0.85,不同λ取值(c)α=0.7、λ=0.8、x=0.85,不同K取值(d)α=0.7、λ=0.8、K=1,不同x取值频域特性仿真实验结果对比。
从图3中的分数阶超前-滞后补偿器频域特性可以看出,分数阶超前-滞后补偿器所表达的频域特性具备范围性,其幅值特性在低频段、高频段表现为不同的调节效果,相位特性只针对指定角频率ωb及其不为0周边频域段。阶次的调整能够改变幅值特性、相位特性,所以分数阶超前-滞后补偿器的加入能够在有效提高控制系统带宽的同时,不造成因控制系统高频段增益幅值特性增大而带来的对高频噪声信号的敏感性。
根据图2,得到加入分数阶超前-滞后补偿器前,反馈控制系统从输入R到输出Y的传递函数:
闭环误差传递函数为
加入分数阶超前-滞后补偿器后,反馈控制系统传递函数变为
闭环误差传递函数变为
在频域范围内,s=jω,根据式(10)~式(14),可得
式中,AF為分数阶超前-滞后补偿器的幅值特性;AC、AE分别为反馈控制系统加入分数阶超前-滞后补偿器前的闭环幅值特性及闭环误差幅值特性;?C、?E分别为反馈控制系统加入分数阶超前-滞后补偿器后的闭环幅值特性及闭环误差幅值特性。
由此,系统加入分数阶超前-滞后补偿器后的闭环幅值特性变化值为
闭环误差幅值特性变化值为
将式(15)代入式(16)中,可以推导出AF与ΔAC、ΔAE具备以下关系:
由于反馈控制系统在低频域范围内,闭环幅值特性趋近于0,也即AC(ω)|ω→0=?C(ω)|ω→0=0,而闭环误差幅值特性主要存在于低频域范围内,所以在低频域范围内,存在
根据式(19)可确定分数阶超前-滞后补偿器参数,以实现分数阶反馈控制方法准确表达被控对象所需闭环误差幅值特性。
3 实验
3.1 实验系统及模型参数辨识
本文方法的实验验证在PMLSM龙门运动平台上进行。如图4所示,该平台采用PMLSM作为致动器,且每个电机均配备直线光栅尺以采集运动信息,实现PMLSM系统的闭环反馈控制。本文在SCALEXIO控制器中实现所提控制方法,并对PMLSM系统进行实时运动控制。
根据所提PMLSM闭环辨识方法开展参数辨识实验。辨识过程中的PMLSM系统输入电流及反馈电流如图5所示,可以看出,开环辨识条件下,实际测量电流与规划扫频信号之间存在相移与幅值衰减,而闭环辨识能够有效提高电流信号的跟随精度,并且抑制电流波动,从而提高参数辨识准确性。
在此基础上,根据式(13)所示辨识模型,本文使用最小二乘法对扫频信号辨识实验数据进行拟合,得到PMLSM系统模型传递函数:
图6对比了开环控制下,开/闭环辨识模型的响应位移,可以看出,闭环辨识模型响应与PMLSM系统响应具备较高的一致性,而开环辨识模型响应与PMLSM系统响应之间存在较大误差。
3.2 PMLSM跟随误差实验
根据式(20)辨识模型,结合Ziegler-Nlichols参数整定方法及多次参数调整实验,最终确定PID控制器参数kP=1553.12、kI=131.65、kD=13.63。在此基础上,结合式(10)、式(15)、式(19),可以求得分数阶超前-滞后调节器参数K=2.514、λ=7.5946×10-4、x=0.3978、α=1.1066。由此,可以得到分数阶超前-滞后补偿频域特性,如图7a所示。反馈控制系统在加入超前-滞后补偿器前后的闭环频域特性对比及闭环误差幅值特性对比如图7b、图7c所示,可以看出,分数阶超前-滞后调节器能够有效增大反馈控制系统带宽,从而使反馈控制系统误差增益特性得到抑制,同时,保证闭环控制系统高频段的响应特性不发生变化。
在PID控制器及分数阶超前-滞后补偿器参数选定后,本文采用正弦运动规划、三次曲线函数运动规划以及圆轨迹运动规划作为输入信号开展PMLSM运动误差对比实验。三次曲线函数为
式中,ta、tc分别为三次曲线函数的加速时间与匀速时间。
图8所示是本文所提方法与PID反馈控制方法的正弦运动跟随误差实验结果,表1所示是实验两种方法跟随误差的均方根误差(root mean square error,RMSE)及平均绝对误差(mean absolute error,MAE)等数据对比结果。其中,|MAX|表示跟随误差的最大绝对值,实验结果表明,PMLSM系统跟随误差会随着控制信号频率的增大而增大,本文所提分数阶反馈控制方法能够保证PMLSM系统在不同频率的正弦运动规划实验中均具备较优的跟随精度,相较于PID反馈控制方法,跟随误差的RMSE可降低至少82.47%。
同时,本文对三次曲线函数规划进行了不同反馈控制方法的比对实验,图9和表2所示是本文所提方法与PID反馈控制方法在三次曲线函数运动规划下的轨迹跟随实验结果。结果表明,本文所提方法能够在很大程度上减小PMLSM系统跟随误差,相较于PID反馈控制方法,跟随误差的RMSE降低了86.02%,实现了PMLSM系统的快速高精度定位。
在单电机跟踪运动控制实验的基础上,本文也将控制算法应用于龙门平台的Y轴双电机,通过双轴运动系统测试本文所提控制算法的跟踪性能。图10所示为龙门平台圆轨迹运动的位移与跟踪误差实验结果,可以看出,本文方法能够有效提高龙门运动平台中每个电机跟随精度,双轴轨迹运动精度也得到了较好的提高,相较于PID反馈控制方法,本文方法的圆轨迹误差RMSE降低了85.61%。因此,系列实验数据对比及分析结果表明,本文分数阶反馈控制方法可有效提高PMLSM系统的运动跟随精度。
4 结论
本文通过建立带电流环闭环控制的PMLSM系统模型,实现对运动系统的闭环辨识,提高了参数辨识准确性。在此基础上,结合分数阶控制理论提出了分数阶反馈控制系统方法,并通过闭环误差幅值特性,明确了分数阶超前-滞后补偿器参数选定方法,实现了PMLSM系统控制频域特性的准确表达,从而能够有效提高PMLSM运动系统的跟随精度。系列实验结果表明,带电流环的闭环辨识方法可以获取更适于实际运动系统的模型,据此设计的分数阶反馈控制方法可有效提高PMLSM系统运动跟随精度。在不同运动规划下,相较于PID反馈控制方法,本文方法能将跟随误差的RMSE值减小至少82.47%,验证了本文所提基于闭环辨识模型的分数阶反馈控制方法在提高PMLSM系统运动精度方面的有效性和先进性。
参考文献:
[1]HU Chuxiong,OU Tiansheng,CHANG Haonan,et al. Deep GRU Neural Network Prediction and Feedforward Compensation for Precision Multiaxis Motion Control Systems[J]. IEEE/ASME Transactions on Mechatronics,2020,25(3):1377-1388.
[2]LIU Yachao,GAO Jian,ZHONG Yongbin,et al. Extended State Observer-based IMC-PID Tracking Control of PMLSM Servo Systems[J]. IEEE Access,2021,9:49036-49046.
[3]陶大錦,柯大观,袁柳斌,等. 直线伺服系统模型参数辨识及其实验研究[J]. 中国机械工程,2013,24(7):915-921.
TAO Dajin,KE Daguan,YUAN Liubin,et al. Model Parameter Identification and Experimental Study of Linear Servo System[J]. China Mechanical Engineering,2013,24(7):915-921.
[4]杨亮亮,时军,鲁文其,等. 直线伺服系统时滞参数辨识与补偿研究[J]. 机械工程学报,2018,54(5):193-201.
YANG Liangliang,SHI Jun,LU Wenqi,et al. Research on Identification and Compensation of Delay Parameters in Linear Servo System[J]. Chinese Journal of Mechanical Engineering,2018,54(5):193-201.
[5]ZHANG J D,GAO J,ZHANG L Y,et al. Novel Dynamic Microactuation Method for Tracking-error Reduction of Permanent Magnet Linear Synchronous Motors[J]. IEEETransactions on Industrial Electronics,2022,69(9):9165-9175.
[6]TAN Qiang,WANG Mingyi,LI Liyi,et al. Research on Noninteger Pole Number for Segmental Permanent Magnet Linear Synchronous Motor[J]. IEEE Transactions on Industrial Electronics,2021,68(5):4120-4130.
[7]ZHAO Jing,MOU Quansong,ZHU Congcong,et al. Study on a Double-sided Permanent-magnet Linear Synchronous Motor with Reversed Slots[J]. IEEE/ASME Transactions on Mechatronics,2021,26(1):3-12.
[8]TAN Lingwei,GAO Jian,LUO Yuheng,et al. Super-twisting Sliding Mode Control with Defined Boundary Layer for Chattering Reduction of Permanent Magnet Linear Synchronous Motor[J]. Journal of Mechanical Science and Technology,2021,35(5):1829-1840.
[9]ZHANG Wenjing,NAN Nan,YANG Yifang,et al. Force Ripple Compensation in a PMLSM Position Servo System Using Periodic Adaptive Learning Control[J]. ISA Transactions,2019,95:266-277.
[10]WANG Mingyi,YANG Rui,TAN Qiang,et al. A High-band width and Strong Robust Current Control Strategy for PMLSM Drives[J]. IEEE Access,2018,6:40929-40939.
[11]WANG Mingyi,YANG Rui,ZHANG Chengming,et al. Inner Loop Design for PMLSM Drives with Thrust Ripple Compensation and High-performance Current Control[J]. IEEE Transactions on Industrial Electronics,2018,65(12):9905-9915.
[12]XI Jingsi,DONG Zeguang,LIU Pinkuan,et al. Modeling and Identification of Iron-less PMLSM End Effects for Reducing Ultra-low-velocity Fluctuations of Ultra-precision Air Bearing Linear Motion Stage[J]. Precision Engineering—Journal of the International Societies for Precision Engineering and Nanotechnology,2017,49:92-103.
[13]吳路路,韩江,田晓青,等. 无偏差最小二乘法伺服控制系统参数辨识[J]. 中国机械工程,2016,27(1):109-113.
WU Lulu,HAN Jiang,TIAN Xiaoqing,et al. Parameter Identification of Unbiased Least Square Servo Control System[J]. China Mechanical Engineering,2016,27(1):109-113.
[14]梁健强,吴金洲,魏巍. 基于辅助变量的永磁同步直线电机系统辨识研究[J]. 微电机,2021,54(11):52-57.
LIANG Jianqiang,WU Jinzhou,WEI Wei. Research on System Identification of Permanent Magnet Synchronous Linear Motor Based on Auxiliary Variables[J]. Micromotors,2021,54(11):52-57.
[15]岳颀. 基于改进遗传算法的内埋式永磁同步电机参数辨识[J]. 微电机,2015,48(8):79-82.
YUE Qi. Parameter Identification of Embedded Permanent Magnet Synchronous Motor Based on Improved Genetic Algorithm[J]. Microelectric Machine,2015,48(8):79-82.
[16]HAUSMANN S B,VARGAS A M,MATHIS A,et al. Measuring and Modeling the Motor System with Machine Learning[J]. Current Opinion in Neurobiology,2021,70:11-23.
[17]张鹏,王文格,付霞,等. 基于闭环自适应辨识的速度环PI参数自整定[J]. 中国机械工程,2016,27(5):639-645.
ZHANG Peng,WANG Wenge,FU Xia,et al. Self-tuning of PI Parameters of Velocity Loop Based on Closed-loop Adaptive Identification[J]. China Mechanical Engineering,2016,27(5):639-645.
[18]ZHONG Yongbin,GAO Jian,ZHANG Lanyu. Fractional-order Feedforward Control Method for Permanent Magnet Linear Synchronous Motor Based on Frequency-domain Adjustment Theory[J]. Mechanical Systems and Signal Processing,2023,190:110115.
[19]ZHONG Yongbin,GAO Jian,ZHANG Lanyu. Adaptive Fractional-order Anti-saturation Synchronous Control for Dual-motor Systems[J]. Applied Sciences,2023,13(4):2307.
[20]CHEN Syuanyi,LI Tunghung,CHANG Chihhun. Intelligent Fractional-order Backstepping Control for an Ironless Linear Synchronous Motor with Uncertain Nonlinear Dynamics[J]. ISA Transactions,2019,89:218-232.
(编辑 袁兴玲)

