考虑轮胎载荷转移影响的复合式胎压监测补偿修正方法

唐先智　张晓壮　郝少澎　王波　张宇

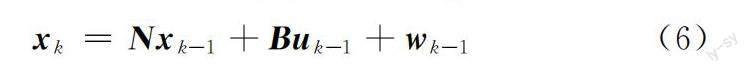
摘要：车辆在加速和爬坡时会产生载荷转移，导致胎压监测结果受到干扰，针对该问题，提出了基于轮胎载荷的胎压监测结果补偿修正方法。基于双重无迹卡尔曼滤波对车辆质量和质心位置进行了双重估计，采用递推最小二乘法（RLS）进行了坡度识别。利用轮胎转毂试验台进行试验，得到载荷、车速、胎压和轮胎下沉量的数据，拟合了载荷、车速、胎压与轮胎下沉量的关系表达式。利用坡度识别，通过车辆质量和质心位置的估计，计算四轮独立载荷，修正相应的轮速脉冲。试验结果表明：没有载荷修正的胎压计算值存在20%的稳定误差和大幅度波动；加入载荷修正，虽有一定的迟滞性和波动，但会很快收敛到真实值，稳定误差在5%以内，解决了因载荷变化导致胎压估算不准确的问题。

关键词：轮胎载荷转移；复合式胎压监测；双重无迹卡尔曼滤波；轮胎转毂试验台

中图分类号：U463.6

DOI：10.3969/j.issn.1004-132X.2023.23.012

开放科学（资源服务）标识码（OSID）：

Compensation and Correction Method of Compound Tire Pressure Monitoring

Considering Influences of Tire Load Transfer

TANG Xianzhi¹ZHANG Xiaozhuang¹HAO Shaopeng¹WANG Bo¹ZHANG Yu²

1.School of Vehicle and Energy，Yanshan University，Qinhuangdao，Hebei，066004

2.Luan Automobile Technology Co.，Ltd.，Changzhou，Jiangsu，213000

Abstract：The vehicle would produce load transfer during acceleration and hill climbing，which led to the interference of tire pressure monitoring results. To address this problem，a tire pressure monitoring result compensation correction method was proposed based on tire loads herein. Dual estimation of vehicle mass and center of mass position was carried out based on Dual-UKF，and recursive least square （RLS） was used for slope identification. The data of load，vehicle speed，tire pressure and tire sinkage were collected by using a tire rotation hub test bench. The relational expression of load， speed， tire pressure and tire sinking were obtained by fitting the data. Using slope identification，the four-wheel independent load was calculated by estimating the vehicle mass and center of mass position to correct the corresponding wheel speed pulse. The test results show that the calculated values of tire pressure without load correction have 20% stable error and large fluctuation. with load correction，although there is a certain hysteresis and fluctuation，it will eventually converge to the true value quickly and the stable error is within 5%，which solves the problem of inaccurate tire pressure estimation due to load changes.

Key words：tire load transfer； composite tire pressure monitoring； dual unscented Kalman filtering（Dual-UKF）； tire hub test bench

收稿日期：2022-12-14

基金項目：河北省高等学校科学技术研究重点项目（ZD2019063）；国家自然科学基金（51505414）

0 引言

在汽车行驶安全方面，制动防抱死系统（ABS）、胎压监测系统（TPMS）和安全气囊被称为保证汽车安全行驶的三大重要配置。对胎压监测系数的研究主要分为三类：直接式胎压监测、间接式胎压监测和复合式胎压监测^［1］。

直接式胎压监测通过安装在轮胎上的传感器实时更新胎压胎温，并且可以检测出轮胎是否出现漏气。张威等^［2］采用单片机，通过传感器采集压力和温度数据，由液晶显示器显示胎压和温度，并且增加了储存器，能够在系统断电时保存数据。 郭玉言^［3］基于ARM处理器对直接式胎压监测系统进行了设计，利用WIFI模块与手机APP进行了连接。韩志嵘等^［4］对大型汽车直接式胎压监测进行了设计，不仅可以实时监测胎压和胎温，还可以自行调节胎压。虽然直接式胎压监测对胎压有着较高的测量精度，但是成本较高，使用寿命有限，并且容易被外界信号干扰造成数据丢失。

间接式胎压监测系统主要是基于ABS的轮速信号，估算方法一般为轮速脉冲法、频域法、动力学模型法和参数辨别法。周福强等^［5］对实车采集的数据通过快速傅里叶变换进行频域分析，采用最高峰值法获得轮胎扭转频率，从而获得胎压。单经纬^［6］首先对轮速信号进行处理，采用分段线性差值法对轮速信号进行了重构，通过快速傅里叶变换进行频谱分析，提取轮胎共振频率判断轮胎是否缺气。彭加耕等^［7］通过里程修正轮胎磨损量，基于BP神经网络对四轮同时缺气进行辨识。王宝琳等^［8］采用BP神经网络修正车辆转弯所造成的内外侧轮胎脉冲存在差异的问题，利用三均值比较法对右后轮胎压进行判断。罗新帅^［9］、董倩倩^［10］基于轮速脉冲法和频域法设计了间接式胎压监测算法，对两种方法进行融合实现了四轮同程度欠压识别。尹龙川^［11］通过轮速分析，融合频率法和半径法对胎压进行监测。间接式胎压监测成本低，但是无法显示胎压值，只能在胎压达到报警线时提示驾乘人员。

复合式胎压监测安装一个或两个直接式胎压压力传感器，使用间接式的方法实现对其他轮胎胎压的估算。刘澍^［12］嵌入了基于同侧轮轮速脉冲比较法的间接式胎压监测单轮算法，并在直线工况下实现了单轮缺气定位报警。吴飞龙等^［13］设计的复合式胎压监测方法在轮胎只有一个轮胎单独欠压或是两个轮胎欠压情况下使用半径法，其余情况使用频率法。复合式胎压监测系统成本比直接式胎压监测系统低，并且还可以实时监测轮胎胎压。然而，车辆在实际行驶过程中，由于加速度、道路坡度的存在，车辆会产生载荷转移，导致前轴载荷与后轴载荷分配情况发生变化；并且油箱内现有的油量、载客量、载货量等变化，也会导致轴荷分配发生变化；车辆人员的数量和分布情况不同，也会在一定程度上影响轴荷分配。载荷的变化会影响胎压监测的准确性。

基于以上问题，本文采用轮速比较法设计复合式胎压监测系统，并且对车辆质量、质心位置、道路坡度进行识别，对不同载荷下胎压与轮胎下沉量进行分析，验证载荷和胎压之间存在一定的关系式，提出了载荷补偿修正胎压的方法，并且通过试验验证了方法的正确性。

1 车辆动力学模型搭建

本文以四轮独立悬挂、前置前驱、前轮转向车辆为研究对象，测量值信号来自于车载传感器和CAN总线。

根据牛顿第二定律建立质量与坡度估计所需的车辆纵向动力学模型，如图1所示。

由牛顿第二定律进行受力分析可得到车辆在坡道上的纵向动力学表达式：

式中，δ_m为车辆换算质量；v纵向速度；F_t为车辆驱动力；F_i为坡道阻力；F_w为空气阻力；F_f为滚动阻力；T_m为滚动阻力矩；i_g为变速器传动比；i₀为主减速器传动比；η_t为传动效率；r₀為车轮半径；C_d为空气阻力系数；A为车辆迎风面积；ρ为空气密度；f为滚动阻力系数；m为车辆质量；g为重力加速度，取9.8 m/s²；α为道路坡度。

2 基于Dual-UKF的车辆参数估计

选择合适的滤波算法，利用汽车纵向动力学对车辆参数进行估计是核心环节。在车辆使用过程中，车辆上发生的加载或卸载会导致整车质量和质心位置变化，这些变化会导致前后轴载荷不同，从而使后轮车轮轮速脉冲发生变化，导致胎压的计算估计值增大或减小，所以，为了减小这些影响，在传统估计方法中，会将质心位置和整车质量等参数直接作为常数来使用，没有考虑车辆参数的改变对结果造成的影响。双重无迹卡尔曼滤波算法（Dual-UKF）的优点在于可将可能变化的车辆参数量考虑进去，并且考虑了车辆参数量与状态量之间的互相影响关系（互为输入输出），提高估计准确率，因此本文基于双重无迹卡尔曼滤波算法实现对车辆质量与车辆质心位置的高效追踪估计，从而对胎压估计值进行修正。

经典卡尔曼滤波的系统状态方程是线性的。对于线性系统，其状态空间表达式如下：

式中，N为状态转移矩阵；B、H为转换矩阵；x_k为状态量；u_k-1为控制量；w_k-1为过程噪声；v_k为测量噪声；k为离散时间。

先验估计误差、协方差计算为

式中，X^－_k为先验状态估计值；P－_k为先验状态协方差；Q为过程噪声的协方差；P_k－1为后验状态协方差。

后验估计更新计算误差协方差为

式中，X^_k为当前状态的估计值；Z_k为观测量；K_k为卡尔曼增益。

建立考虑参数变化的车辆状态空间方程与观测方程如下：

式中，θ～_k为状态量；f（x_k，θ～_k，u_k）、h（x_k，u_k）为多元函数式；w_s，k为车辆状态估计时的系统过程噪声，其协方差为Q_s；v_s，k为车辆状态估计时的测量噪声，其协方差为R_s；q_k是被估计的车辆参数量与状态量。

观测量Z_k表示为

式中，a_x为纵向加速度；a_y为侧向加速度；ω_r为横摆角速度。

x_k为车辆的参数量，x～_k表示在状态估计时将参数视作定值，要估计的车辆参数量与状态量分别如下：

式中，m为整车质量；a₀为质心至前轴距离；v_x为纵向车速；v_y为侧向车速；β为转向盘转角。

输入量u_k为

式中，δ为前轮转角；ω_ij为四轮轮速信号；T_ij为四轮扭矩。

输入量离散方程表示如下：

其中，T_s为最小仿真步长，输入量基于前项欧拉法进行离散化处理，使其可以正常输出。

由于车辆参数量x_k的变化速率缓慢，因此在第一层估计结果出来后，将车辆参数量认作常数，得到参数方程与观测方程如下：

式中，w_var，k为车辆状态估计时的系统过程噪声，其协方差为Q_var；v_var，k为车辆状态估计时的测量噪声，其协方差为R_var。

利用CarSim创建测试工况，输出所需的控制和测量参数量，利用MATLAB/Simulink搭建Dual-UKF滤波器，对比CarSim输出的车辆行驶状态以验证估计结果的正确性。

车型选择CarSim中的C级车，设置驾驶员模型中的控制量。仿真路面设置为附着系数μ=0.9的平坦路面，以60 km/h的初速度进行仿真，轮缸压力设置为p_b=0.5 MPa，以0.5 Hz频率的正弦波信号作为转向盘输入，角度范围为［-90°，90°］。

通过参数调试得到双重无迹卡尔曼滤波参数估计器中的过程噪声Q_varc=diag（1，0.1，1），测量噪声R_varc=0.01I_3×3；状态估计器的过程噪声Q_vars=10^-8I_3×3，测量噪声R_vars=I_3×3。

CarSim的C级车的整车质量m=1655 kg，质心至前轴的距离a₀=1.30 m。整车质量估计如图2所示，质心位置至前轴的距离如图3所示。

由图2与图3可知，随着仿真的进行，整车质量m、质心至前轴的距离a₀估计量有所波动，但最终都收敛到对应的真实值附近，因此该观测器可以实现对车辆质心及质量预测。

3 基于RLS算法的道路坡度识别

由于递推最小二乘（RLS）估计算法相比其他方法需求的参量更少、实时性更好，且对单输入单输出系统而言，无需额外先验条件，因此本文选用RLS估计算法实现对路面坡度的估计。

联立式（1）～式（5），得到车辆纵向动力学公式表达：

建立n阶自回归（AR）模型：

式中，y（t）为系统输出；a₁，a₂，…，a_n为待估计参数；y（t-1），…，y（t-n）为测量数据；ε（t）为系统白噪声，均值为零且方差大于零。

递推最小二乘法参数估计表达式如下：

式中，θ^（t+1）为待估计参数；K（t）为增益矩阵；P（t）为协方差矩阵；φ（t）为输入向量；λ为遗忘因子。

由于新旧观测值相互影响较小，故令遗忘因子λ=0.95。根据RLS算法，由式（24）～式（26）可得路面坡度估计值α为

为验证坡度估计算法模块有效性，同样利用MATLAB/Simulink搭建状态估计观测器模型，并与CarSim中设定好的车辆模型进行联合仿真测试，仿真流程如圖4所示。图4中，T_总表示发动机输出扭矩，a_x表示纵向加速度，V_x表示纵向速度，m_0表示汽车质量初始值。CarSim输出信号至MATLAB/Simulink所搭建好的模型中，输出估计的坡度值。

中道路条件设置为30°的坡度，仿真车辆速度为40 km/h匀速，仿真结果如图5所示。

由图5可知，真实路面坡度值在26%～32%之间，观测结果在5s内快速收敛到真实坡度值附近，估计误差在5%之内，该观测器具有较高的估计精度且稳定性较好，可以实现对道路坡度的预测。

4 载荷对轮速的影响分析

为进一步探究载荷对轮胎滚动的影响机制，本文利用轮胎转毂试验台采集轮胎在不同垂向载荷、胎压状态下的轮胎变形量信息，根据试验结果建立各参量之间的关系。

搭建的单轮转毂试验台如图6所示，该试验台由驱动电机、转毂、气泵、压力缸、单边悬架、轮胎以及相应的传感器组成，转毂试验台采用SC160复动气缸进行加载，通过打气泵使气体经过油水分离器的过滤作用于加载气缸上，控制复动气缸输出压力模拟载荷，并将载荷施加在麦弗逊悬架的减振弹簧及摆臂上，最终实现控制轮胎所受到的垂直载荷，调节范围为0～10 kN。同时利用轮胎压力传感器、激光位移传感器、气缸压力传感器来获取对应的载荷、胎压、轮胎变形量等信息。

当轮胎压力固定时，随着轮胎加载力的增大，轮胎的变形量逐渐增大。根据日本学者FUJIMOTO经验结果^［14］，轮胎下沉量经验公式可表示如下：

式中，F_z为载荷，kN；p为胎压，kPa；σ为下沉量，mm；a₁、b₁、c₁、d₁、e₁为待标定系数。

本文选择的轮胎型号为Cross Wind HP品牌的205 60 R16 92H；胎压的选择为标准胎压、85%标准胎压、70%标准胎压；载荷从2.0 kN开始，以0.5 kN为间隔，逐渐增大载荷至6.0 kN；载荷5 kN，胎压分别为150 kPa（1.5 bar）、240 kPa（2.4 bar）时，车速以10 km/h为间隔，从40 km/h依次增大至120 km/h。建立轮胎承受载荷、轮胎气压和车速与轮胎变形量对应关系，得到胎压、载荷与轮胎下沉量的变化关系，如图7所示，车速与轮胎下沉量的关系如图8所示。

由图7可以看出，随着对轮胎施加的载荷增大，轮胎的下沉量也增大，并且在同一载荷的情况下，胎压越高，轮胎下沉量越小。载荷2～6 kN处于线性区域，并且在胎压较低的情况下，变形量变化范围也会增加。

由图8可以看出，车速对轮胎变形量影响较小，当车速从40 km/h增加至120 km/h时，在轮胎低压的情况下，轮胎下沉量变化为2.4 mm，相对于轮胎低压状态，标准胎压时，从低速至高速，轮胎下沉量不到2 mm。

利用式（28）对图7和图8中的试验数据进行拟合，得到未知系数a₁、b₁、c₁、d₁、e₁，拟合后的下沉量经验公式为

式中，E₁、F₁为整理后的拟合系数，E₁为1.771、1.747、1.476，F₁为10.43、8.594、7.524。

为验证载荷是否对轮速脉冲信号有影响，将测试轮胎安装在试验车上，通过在车内加载或卸载，模拟后轴车轮分别在2.0 kN、4.0 kN、6.0 kN的载荷工况，通过使用10 kg的沙袋改变后轴轮胎垂直载荷，车辆以60 km/h速度做匀速直线行驶运動；通过试验车的车载CAN通信网络，利用Kvaser leaf v2 CAN总线分析仪，从总线上采集所需轮速脉冲等信号，并将所采集到的信号以.log文件形式储存至指定文件夹^［12］，之后利用MATLAB建立函数脚本，按照试验车型的CAN网络通信协议，针对所需信号进行解析、换算、滤波、修正^［9］，得到各组试验下的轮速信号，结果如图9a、图9b、图9c所示，各组载荷速度差值对比如图9d所示。

将三种不同载荷下的前后轮速滤波处理后做均差，结果如图9d所示，结合图7可以看出，随着载荷的增大，后轮轮胎下沉量增大，轮胎滚动半径减小，使车辆前后轴之间的轮速脉冲差值增大，后续会影响轮速法计算得到的实际胎压值。

5 基于载荷修正的复合式胎压监测算法

复合式胎压监测是在间接式胎压监测算法基础上，引入一个或两个胎压压力传感器的信息用以估算未安装轮胎压力传感器车轮的胎压。现有的复合式胎压监测均以轮速法为基本方法。

轮速脉冲比较法的原理是利用ABS系统中轮速传感器的脉冲信号计算各个车轮转速，由于轮胎缺气时其滚动半径会减小转速会增加，故通过对比四轮轮速脉冲信号之间的差异就可以判断出轮胎是否出现缺气状况，复合式胎压监测系统主要流程如图10所示。

脉冲数组的累计是通过累计轮速脉冲数据的方法放大各轮速信号N_i之间的差异。为方便数据后期处理，更新之前首先对轮速信号进行归一化处理。同时也利用轮速信号累计的过程计算车辆速度、加速度、方向转角等状态值在累计期间的均值，用于判断样本可靠性，决定本组样本的剔除或修正。本文选取固定长度N_std=5000，即每累计5000个轮速脉冲样本进行一次更新。其中脉冲数组的累计具体步骤与部分表达式如图11所示。其中，N_i为轮速信号（i=0，1，2，3），Acc±为采样周期内的加速度、减速度均值，v为车速信号值，str为转向盘转角信号值，Deg_r，l为采样周期内右转角、左转角均值，N_i为轮速脉冲样本数据，v为采样周期内的车速均值。

为提高更新速率，本文采用滚动时域算法数据结构，数据结构如图12所示，以N_std为固定窗口长度，按时域顺序依次存放样本数据，数据队列的方式保证了队列中的样本数据维度不变。

利用自适应双重叠加滤波器模块对轮速信号进行预处理。之后使用Busmaster中的Replay功能，对采集到的不同阶梯载荷下的匀速直线行驶工况样本进行回放仿真，利用标准轮速脉冲值与胎压计算公式进行拟合标定。胎压计算拟合公式如下：

式中，p_i为各非基准轮胎压，kPa；p₀为基准轮胎压，kPa；A_i、B_i为胎压计算公式标定系数；N^_i为各非基准轮修正并滤波后轮速脉冲样本值，i=1，2，3；N^₀为基准轮滤波后轮速脉冲样本值。

A_i、B_i标定后的胎压拟合系数数值为

对标定后的胎压拟合公式设计测试工况，测试方法按照GB/T 26149《乘用车轮胎气压监测系统的性能要求和试验方法》进行，测试内容为直线行驶工况胎压计算显示精度测试。设计阶梯载荷试验工况，以150 kg载荷工况为基准进行胎压计算公式参数拟合，待参数拟合完成后依次进行一次卸载与两次阶梯加载过程。为保证试验结果的准确性，测试以60 km/h速度进行匀速直线行驶，并保证每个载荷区间段均有足够的有效样本数量进入。

试验车辆为前置前驱车型，因为发动机舱、变速箱等因素，导致车辆的簧上载荷大部分都分布于前轴，在车内载荷发生变化时，前轴载荷发生的变化相对后轴载荷变化较小，本文所设计的复合式胎压监测，选择的基准轮为左前轮和右前轮。图13所示是车辆载荷发生变化，但没有对载荷进行修正所计算得到的两后轮胎压结果。

由图13可以看出，由于标定过程中未考虑载荷变化带来的影响，所以当载荷差值发生较大变化时，计算结果出现较大的稳态误差。以上述工况为例，标准胎压为230 kPa时，最大计算值为246.3 kPa，最小计算值为198.6 kPa，计算误差波动范围超过20%。

车辆在行驶过程中，轮胎的垂向载荷会根据不同的车辆工况和路况的改变而发生改变。轴荷会根据加速度的变化而发生载荷转移，利用车辆动力学对四轮独立载荷进行计算，实现实时更新，具体计算公式为

式中，a为质心至前轴的距离；b为质心至后轴的距离；l_f为前轴轮距；l_r为后轴轮距；h为车辆质心高度。

结合第二节对m₀、a₀的估计结果可以得到整车质量分布在车辆后轴的载荷得到修正量，具体表达式为

结合式（30），可以得到修正后的胎压计算公式：

式中，Δ为载荷影响修正量；τ为拟合换算系数；a₁为车辆轴距。

第三节对坡度识别的结果显示，坡度识别具有一定的迟滞性，并且仅通过车辆动力学模型实现坡度高精度识别或实现变坡度高精度识别较困难，所以本文利用坡度识别对路面进行筛选，若路面坡度过大，四轮独立载荷变化较大，则此段的数据会被过滤，以保证数据的准确性，实现对胎压的准确识别。图14所示为车辆载荷发生变化且对载荷进行修正后所计算得到的两后轮胎压结果。

分析上述试验结果，由于滤波算法估计参数的滞后性，当载荷差值发生较大变化时，计算依然出现小波动的偏移误差，但随着估计值的逐步趋稳，胎压计算值收敛至胎压真实值附近。如图14所示，标准胎压为230 kPa时，最大计算值为238.1 kPa，最小计算值为225.6 kPa，计算误差波动范围被控制在了5%以内，稳态误差得到了很好的控制。

6 结论

（1）基于輪速比较法采用车辆载荷修正复合式胎压监测系统，使用车辆纵向动力学模型基于双重无迹卡尔曼滤波（Dual-UKF）对车辆质量与质心位置进行了双重估计，从CarSim仿真试验中可以看出，该方法有着较高的精度与收敛速度，实现了对目标的跟踪估计。利用递推最小二乘法（RLS）对道路坡度进行了识别，并在CarSim软件中进行了仿真试验，误差在5%左右，验证了算法的可行性。

（2）搭建了轮胎转毂试验台，研究了载荷、车速、胎压与轮胎变形量之间的关系，拟合出轮胎下沉量经验公式。将测试轮胎装入实车，进行了在后轴车轮施加2 kN、4 kN和6 kN不同载荷的试验，将前后轮速滤波处理后取平均作差，发现载荷会导致轮胎轮速发生变化，后续会影响基于轮速法的复合式胎压监测的胎压计算。

（3）通过坡度识别过滤车辆在坡道上行驶的数据，使用Busmaster软件对采集到的不同阶梯载荷下的匀速直线行驶工况样本进行回放仿真，拟合标准轮速脉冲值对胎压的计算。仿真试验表明，没有加入载荷修正时，存在20%的稳定误差和大幅度波动；加入载荷修正，虽有一定的迟滞性和波动，但是最终会很快收敛到真实值，稳定误差在5%以内，解决了因坡度和载荷导致胎压值计算不准确的问题。

参考文献：

［1］王勇. 浅谈胎压监测系统TPMS的类型和标准实施现状［J］. 科技资讯，2017，15（9）：26-27.

WANG Yong. Discuss the Types and Implementation Status of TPMS for Tire Pressure Monitoring Systems［J］. Science & Technology Information，2017，15（9）：26-27.

［2］张威，王宁波，陈美玲. 基于单片机的胎压监测装置设计［J］. 现代信息科技，2022，6（2）：70-74.

ZHANG Wei，WANG Ningbo，CHEN Meiling. Design on Tire Pressure Monitoring Device Based on Single Chip Microcomputer［J］. Modern Information Technology，2022，6（2）：70-74.

［3］郭玉言. 基于ARM的汽车胎压监测系统［J］. 自动化技术与应用，2020，39（12）：173-178.

GUO Yuyan. ARM-based Automotive Tire Pressure Monitoring System［J］. Techniques of Automation and Applications，2020，39（12）：173-178.

［4］韩志嵘，林芸，刘洁. 基于ARM的汽车胎压监测系统［J］. 汽车实用技术，2019（1）：114-115.

HAN Zhirong，LIN Yun，LIU Jie. ARM Based Automotive Tire Pressure Monitoring System［J］. Automobile Applied Technology，2019（1）：114-115.

［5］周福强，王少红，兰宁，等. 基于轮胎扭转高阶频点的汽车胎压监测信号分析［J］. 汽车科技，2021（6）：7-11.

ZHOU Fuqiang，WANG Shaohong，LAN Ning，et al. Analysis of Automobile Tire Pressure Monitoring Signal Based on High Order Frequency Point of Tire Torsion［J］. Auto Sci-Tech. ，2021（6）：7-11.

［6］单经纬. 基于频域特征分析的间接式胎压監测算法研究［D］. 长春：吉林大学，2016.

SHAN Jingwei. The Research of Indirect Tire Pressure Monitoring Algorithm Based on Frequency Domain Feature Analysis［D］. Changchun：Jilin University，2016.

［7］彭加耕，王宇岱，韩宗奇，等. 高速工况下间接式胎压监测的影响因素研究与优化［J］. 汽车技术，2020（9）：45-51.

PENG Jiageng，WANG Yudai，HAN Zongqi，et al. Research and Optimization on Influencing Factors on Indirect Tire Pressure Monitoring in High Speed Driving Conditions［J］. Automobile Technology，2020（9）：45-51.

［8］王宝琳，夏怀成，董倩倩. 车辆转弯工况下间接式胎压监测系统脉冲数的修正［J］. 汽车安全与节能学报，2021，12（4）：507-515.

WANG Baolin，XIA Huaicheng，DONG Qianqian. Correction for Pulse Number of Indirect Tire Pressure Monitoring System under Vehicle Turning Condition［J］. Journal of Automotive Safety and Energy，2021，12（4）：507-515.

［9］罗新帅. 基于轮胎滚动半径和频域特征的间接式胎压监测算法研究［D］. 长春：吉林大学，2021.

LUO Xinshuai. Research on Indirect Tire Pressure Monitoring Algorithm Based on Tire Rolling Radius and Frequency Domain Feature［D］. Changchun：Jilin University，2021.

［10］董倩倩. 基于轮速脉冲数和频率法融合的胎压监测算法研究［D］. 秦皇岛：燕山大学，2021.

DONG Qianqian. Research on Tire Pressure Monitoring Algorithm Based on the Fusion of Wheel Speed Pulse Number and Frequency Method［D］. Qinhuangdao：Yanshan University，2021.

［11］尹龙川. 基于轮速分析的间接式胎压监测算法研究［D］. 武汉：湖北工业大学，2021.

YIN Longchuan. Research on Indirect Tire Pressure Monitoring Algorithm Based on Wheel Speed Analysis［D］. Wuhan：Hubei University of Technology，2021.

［12］刘澍. 直线行驶工况下的复合式胎压监测算法研究［D］. 秦皇岛：燕山大学，2021.

LIU Shu. Research on Compound Tire Pressure Monitoring Algorithm under Straight Line Driving Condition［D］. Qinhuangdao：Yanshan University，2021.

［13］吴飞龙，郭世永. 复合间接式胎压监测机制研究［J］. 青岛理工大学学报，2022，43（1）：106-114.

WU Feilong，GUO Shiyong. Research on Monitoring Mechanism of Compound Indirect Tire Pressure［J］. Journal of Qingdao University of Technology，2022，43（1）：106-114.

［14］庄继德. 汽车轮胎学［M］. 北京：化学工业出版社，1988.

ZHUANG Jide. Automotive Tyres［M］. Beijing：Chemical Industry Press，1988.

（编辑 袁兴玲）

作者简介：唐先智，男，1982年生，副教授。研究方向为智能轮胎、汽车系统动力学及控制、无人驾驶汽车驾驶意图识别及驾乘感受识别、混合动力/电动汽车能量管理策略。E-mail：tangxz@ysu.edu.cn。王 波（通信作者），女，1983年生，博士，讲师。研究方向为节能与新能源汽车和液压混合动力控制策略。E-mail：wangbo2015@ysu.edu.cn。