生问，让课堂绽放亮丽光彩——“运算律总复习”教学的全新尝试

浙江杭州市闻涛小学（310051） 俞 杰

浙江杭州市创意城小学（310056） 伍雪梅

【课前之思】

“运算律总复习”是人教版教材六年级下册的教学内容。这个内容旨在回顾并整理小学阶段所学的运算定律，目标是引导学生自主整理和总结所学的运算规则，并熟练应用这些规则进行计算。这一课常见的教学思路是先集中梳理知识，再进行相应的练习。这种教学方式虽然环节清晰、流程顺畅，但往往难以激发学生的学习兴趣，学生深度思考的机会有限，学习效果不尽如人意。究其原因，是学习过程平淡乏味，学习内容缺乏新意，难以引导学生主动学习和深刻思考。那么，在教学“运算律总复习”时，如何进行创新和突破呢？

首先，分析学生在学习中产生的疑惑。在教材中，需要学生填写的表格只有加法和乘法的五个运算律（如图1）。填写后，学生可能会产生疑问：为什么减法和除法没有相应的运算律？也许教师会引导学生回忆减法的运算性质以及除法的运算性质，但这样学生的疑问可能会进一步增加：为什么加法和乘法的称为“定律”，而减法和除法的称为“性质”？

图1

其次，对某所学校162 名六年级学生进行前测后，笔者发现，60%以上的学生确实有“为什么减法和除法没有相应的运算律？”这样的疑问。在课堂实践中也发现，只要教师稍作引导，许多学生就能意识到并提出“为什么加法和乘法的称为‘定律’，而减法和除法的称为‘性质’？”这类疑问。发现并提出有意义的数学问题能够形成批判性思维和创造性思维，符合数学课程标准中强调的创新意识的培养。因此，笔者认为，在本课中抓住并加强学生内心的疑问是非常有价值的教学目标。

最后，问题的探究和解决也突显本课另一个重要的教学目标，即发展学生的推理意识。在学习某个除法运算性质时，学生需要先运用乘除法之间的关系进行转化，然后根据乘法运算律进行解释（有时还需要进行乘法运算律的变形），最终找到性质和定律之间的联系。整个过程需要严密而清晰的思维，涉及数学符号的推导，可以有效培养学生的推理意识。

基于以上思考和发现，笔者将“生问课堂”模式应用于本课，在保持复习课基本模式“知识唤醒、梳理、结构化，查漏补缺、巩固强化，适度提升、合理拓展”的基础上，着重引导学生参与提问、验证、推理、计算、编题等学习活动，使他们进一步领悟运算律与运算性质之间的联系，增强运算能力、探究能力和提问能力，同时发展推理意识和创新意识，从而使原本单调乏味的复习课焕发新的魅力。

【课堂实践】

一、回顾旧知，唤醒经验

师：大家学习过哪些运算律，还记得吗？

（学生口答，教师板书记录，形成知识整体结构图，如图2）

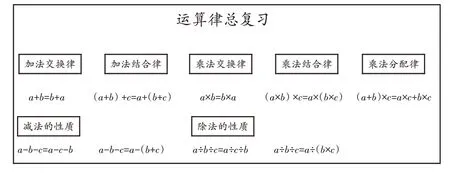
图2

[设计意图：口答、板书等方式，可快速地唤醒学生已有经验；按加、减、乘、除的顺序进行梳理并呈现，既让学生对运算律的整体结构有清晰的印象，也为后面开展“生问课堂”准备好学习材料。］

二、查漏补缺，巩固知识

1.呈现答题情况

师：课前大家都做过一份前测题，现在一起来看看答题情况吧。（出示图3）

图3

2.分析错误原因

师：我们先来看正确率最低的第④题。大家猜一猜，做错的同学是怎么想的？

师（出示图4）：为什么不可以这样做？

图4

生1：这只是在凑数字约分。

生2：他想用乘法分配律，但这个式子不符合乘法分配律的结构。

师：简便运算一定要有依据。可以把17×19 当作一个整体，分别与两个分数相乘再相加。

师（出示图5）：第⑤题可以这样做吗？

图5

生3：这样做不对，因为除法中没有“一个数除以两个数的和等于这个数分别除以两个数之后的和”这样的运算性质。

生4：肯定不对。因为按照正常的运算顺序，先算括号里的加法，再算除法，结果根本不是12。

……

（师生互动，再次明确简便运算的依据。学生自主订正）

[设计意图：教师以前测的形式了解学情，精选六道学生最易出错的习题，为课堂上的精准教学提供了依据。通过深入分析，教师能够发现学生在哪些方面存在不足，从而帮助学生更好地填补空白，并巩固已学。此外，这样能让学生对运算律的特点和相互关系有更深入的思考和理解。］

三、生问引学，深入探究

1.板书提醒，引发生问

师：刚才我们用了黑板上的这些运算律和运算性质来进行简便计算，现在请大家再仔细地看一看它们，有没有疑惑的地方？

生1：为什么加法和乘法的叫运算律，而减法和除法的叫运算性质？

师：生1提的问题还可以怎么描述？

生2：为什么加法和乘法后面都是“律”，而减法和除法后面都是“性质”？

师：也就是定律和性质有什么不同。这真是一个值得研究的好问题。还有其他问题吗？

生3：除法到底有没有分配律？

师：你是怎么想到这个问题的？

生3：因为乘法有分配律，所以我就想除法会不会也有分配律。

师：这也是一个好问题！

生4：除了黑板上写的，还有没有其他运算律或运算性质？

师：你很善于思考，这也是一个非常好的问题。

……

[设计意图：在梳理环节，教师有意将运算律和运算性质分类呈现，上下左右“不对称”的信息（如上为定律下为性质，其中定律乘法有三个，性质除法有两个），是刺激学生观察、比较、生疑的有效材料。引导学生发现和提出问题并感受提问的方法，既让学生的思维得到锻炼，又促使学生展开深度探究。］

2.有序探究，深入感悟

生5：我觉得有除法分配律，因为（a+b）÷c=a÷c+b÷c。

师：你说的这个除法分配律，跟乘法中的某个运算律有关，看得出来吗？先自主探究，再与同桌交流。

生6：我把除法转化为乘法，发现可以运用乘法分配律。（如图6）

图6

师：是的，除法是乘法的逆运算，所以除法运算可以转化为乘法来分析。你们讲的除法分配律，可以用乘法分配律来解释，所以我们不再把它称为运算律，而是称为运算性质。它就是除法的又一个运算性质。

师：a÷b÷c=a÷c÷b和a÷b÷c=a÷（b×c）这两个除法运算性质，会不会也和哪个乘法运算律有关？该怎么解释呢？小组合作探究，并把推导的过程记录下来。

师：这两个除法运算性质与乘法运算律的关联是，一个可以用乘法交换律来解释，另一个可以用乘法结合律来解释。（出示图7）

图7

3.教师引导，学生释问

师：除法的运算性质都可以用乘法运算律进行解释。猜一猜，减法的两个运算性质可以用什么进行解释？

生8：加法运算律。

师：是的，你们到了初中就会知道，减法都能转化为加法来思考，所以用加法的两个运算律就可以解释减法的运算性质了。

师：现在你知道除法和减法的为什么都叫运算性质了吗？

生9：因为它们都可以用运算律来解释。

生10：这些性质都是通过运算定律推导得到的。

师：定律是最基本的原理，而用这些基本原理可以解释的运算规律，就不再叫什么定律，而叫作性质。简单地说，运算性质都可以用运算律推导出来。

[设计意图：通过分步探究除法的运算性质，让学生较好地理解除法运算性质和乘法运算律之间的联系和区别，并认识加法运算律和减法运算性质的关联，从而解决之前提出的问题。探究的过程，是学生开展推理的过程，更是知识实现结构化的过程。］

四、灵活运用，提升能力

师：还剩一个问题——还有没有其他运算律或运算性质？我给出一道练习题，大家边做边思考吧。

出示练习题：在□里填数，在○里填运算符号，使得算式可以简便计算。

（对于每一种填法，教师都要求学生介绍简算的依据。常见的填法有-2.5-0.5 等。教师借助之类的“非典型”填法引出新的运算性质，如a×b÷c=a÷c×b、a-b+c=a+c-b等。）

[设计意图：此题形式简单，答案开放，解题时不但要充分考虑运算之间的关系，而且要有较好的数感来保证运算简便，是对运算律和运算性质的灵活运用。依托算式引出新的运算性质，学生既能顺利解决问题，又能感受到运算性质的丰富。］

【课后有感】

“运算律总复习”这一课的设计实现了高度的实效和创新。对课程的设计和实施进行反思，最成功的部分就是合理引入和有效引导“生问”，这让本课的教学具有鲜明的亮点。

一、生问，让课堂面貌焕然一新

如前所述，传统的“运算律总复习”通常由教师主导知识梳理和题目练习，形式机械、内容单调，学生学习动力不足。然而，将“生问”引入课堂，课堂氛围就会发生明显改变：学生情绪高涨，积极思考，自发地参与探究。这一变化的原因显而易见；学生提出自己感兴趣的数学问题，这些问题不仅得到教师的关注，还被记录在黑板上，成为课堂研究的内容；学生自行探究这些问题，通过交流和讨论，获得属于自己的理解……在这样的学习过程中，学生真正成为课堂的主人，始终参与课堂活动，主动进行思考和探究。

二、生问，让学习活动深度发生

本课的运算律和运算性质，学生之前已学过，因此，复习时如果仅限于记忆和熟练运用，学习将停留在表面层次——没有充分思考，也没有新的收获。然而，引入“生问”环节后，学生提出了具有深度的数学问题（例如定律和性质之间的区别），这促使学生进行更深入的思考。由此，高质量的学习活动，如比较、分析和推理等得以展开，学生开始理解运算律和运算性质之间的内在联系，建构了更为结构化的数学知识体系。这一过程使得课堂呈现深度学习的迷人特质。

三、生问，让素养提升清晰可见

数学学习不仅仅是知识的习得和技能的掌握，还包括能力的发展和素养的提升。在本课中，笔者有意创设数学情境（例如，通过结构化呈现运算定律和性质），引导学生进行观察、比较和思考，并提出一系列有深度的数学问题。这些“生问”活动锻炼了学生的批判性思维和创造性思维，培养了学生的数学眼光和创新意识。同样，在“定律和性质有什么不同”的问题驱动下，学生积极参与了字母表达式的转化和比较，实现了对运算律和运算性质之间的联系沟通。这个过程也促进了学生符号意识和推理意识的培养，学生的能力和素养得到了明显提升。

一节普通的复习课，因为“生问”的引入而焕发出光彩。在数学课程标准强调“问题的发现和提出”的背景下，教师需要更加关注学生的学习心理，更加重视学生的内在疑问，通过更有效的教学设计和教学过程，促进学生运算能力、创新意识等核心素养的发展。