基于LS-SVM方法的变压器铁心振动状态监测

林 聪,何兆磊,朱梦梦,赵 静

(1.云南电网有限责任公司计量中心,云南 昆明 650011) (2.中国南方电网公司电能计量重点实验室,云南 昆明 650217) (3.云南电网有限责任公司电力科学研究院,云南 昆明 650217)

基于新能源的新一代电网呈现出大容量、高电压、智能化、高可靠性和可持续发展的特点[1-3]。智能电网是一种高度智能化、分布广泛的网络,它由先进的监控技术、高性能的电子设备和通信技术组成[4-5]。将各种电子设备引入电力系统会导致产生更复杂的谐波,与现有波形不同,从而加速绝缘老化、过热动力设备,缩短动力设备寿命[6]。上述种种特点对变压器的状态监测与诊断提出了新的要求。对于电力设备状态的监测和评估,通常采用在线和离线方法。近年来,信息技术、计算机技术、传感器技术等新技术的快速发展,使变压器状态监测和故障诊断技术取得了新的进展[7-8],对于变压器实际应用具有一定的意义与作用。基于此,本文以110 kV和10 kV变压器为研究对象,建立了基于最小二乘支持向量机(LS-SVM)算法的变压器故障诊断模型,并通过变压器铁心振动的典型故障状态预测结果验证了LS-SVM算法的精准性,以期为变压器的检修提供技术指导。

1 变压器故障诊断模型

LS-SVM算法将二次规划转化为线性方程组求解问题,加快求解速度的同时有效降低了计算的复杂性,是标准SVM的一种扩展。算法通过式(1)对未知函数进行求解。

f(x)=ωT·φ(x)+b

(1)

式中:f(x)为分类决策函数,ω为超平面的权值矢量,φ(x)为映射函数,b为偏置常数。

给定训练样本集,将最优分类超平面归一化后,对样本集数据进行分类,得到一个带约束的优化问题:

(2)

式中:J为代价函数,λ为正规化参数,ξi为松弛变量。

约束条件为:

yi=ωφ(xi)+b+ξii=1,2,…,N

(3)

式中:yi为约束函数,b为权重向量,N为变量总数,φ(xi)为映射函数变量。

根据约束条件和目标函数建立拉格朗日函数L(·),优化问题变为二次优化问题:

(4)

式中:α为拉格朗日乘数,ξ为松弛变量,αi为拉格朗日乘数分量。

为加快求解速度,基于库恩-塔克条件可得:

(5)

本文将无线射频识别(RFID)标签与振动传感器相融合,以超级电容作为备用供能设备,使其具备振动信号测量功能,通过光伏电池实现RFID传感器的长期持续性工作。自取能RFID传感器设计如图1所示。

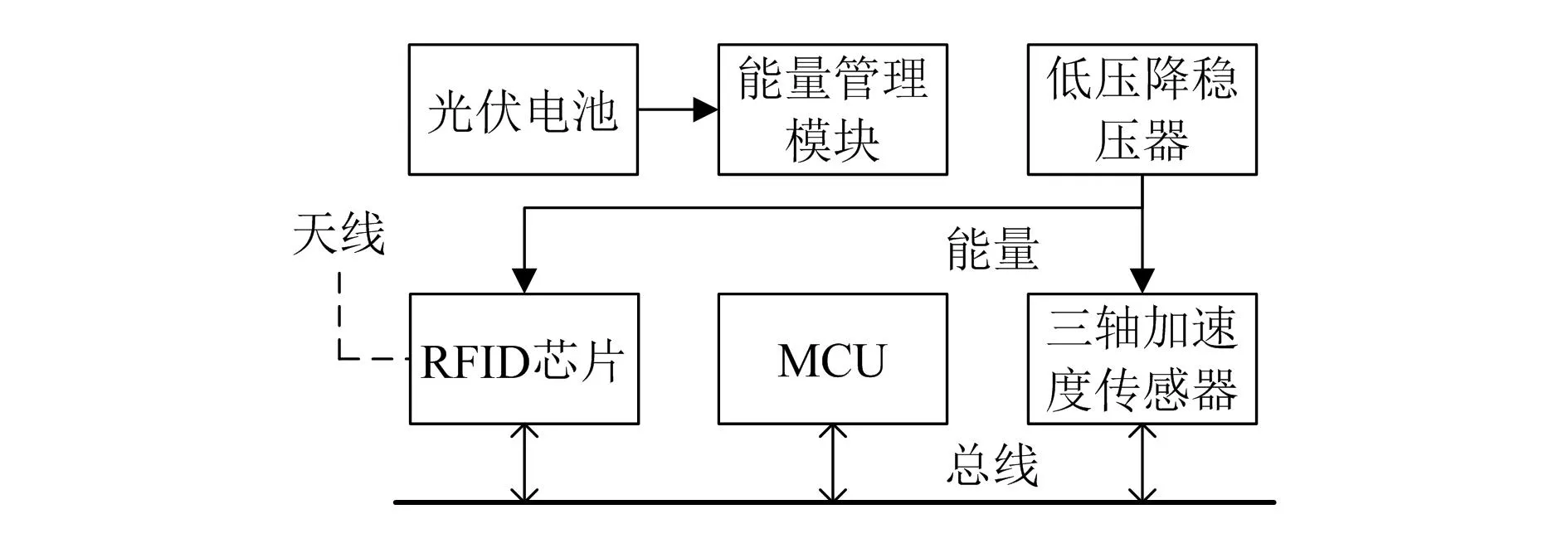
图1 自取能RFID传感器结构图

为确定检修的时间节点,需对变压器进行故障预测。基于变压器状态数据预测变压器的剩余寿命值 (remaining useful life, RUL)值,如图2所示。

图2 变压器故障诊断流程

变压器故障特征提取方法包括时频域、频域以及时域特征提取。时域特征提取方法主要有方差、峭度、倾斜度、峰值以及绝对均值等。其中,频域特征提取对于低频分辨率矿井变压器故障特征的提取效果并不理想。由于受强电磁的干扰,矿井变压器振动信号大多具有非线性和非平稳性,导致时域特征提取的诊断精度不高。因此,本文以Hilbert边际谱图为变压器故障特征参数,并利用时频分析法对其振动信号进行采集。

2 结果与讨论

以云南昆明某110 kV三相变压器和10 kV单相变压器为研究对象,取2020年12月15日—2021年5月15日时间段内的运行数据作为样板数据。变压器正常运行时其振动信号波形和状态指数保持稳定,发生故障时,Hilbert 边际谱波和振动信号的分布会发生畸变,状态指数会偏离正常值。因此,故障预测需要获取海量状态指数信息用于训练故障预测模型。针对变压器进行故障预测,其流程如图3所示。

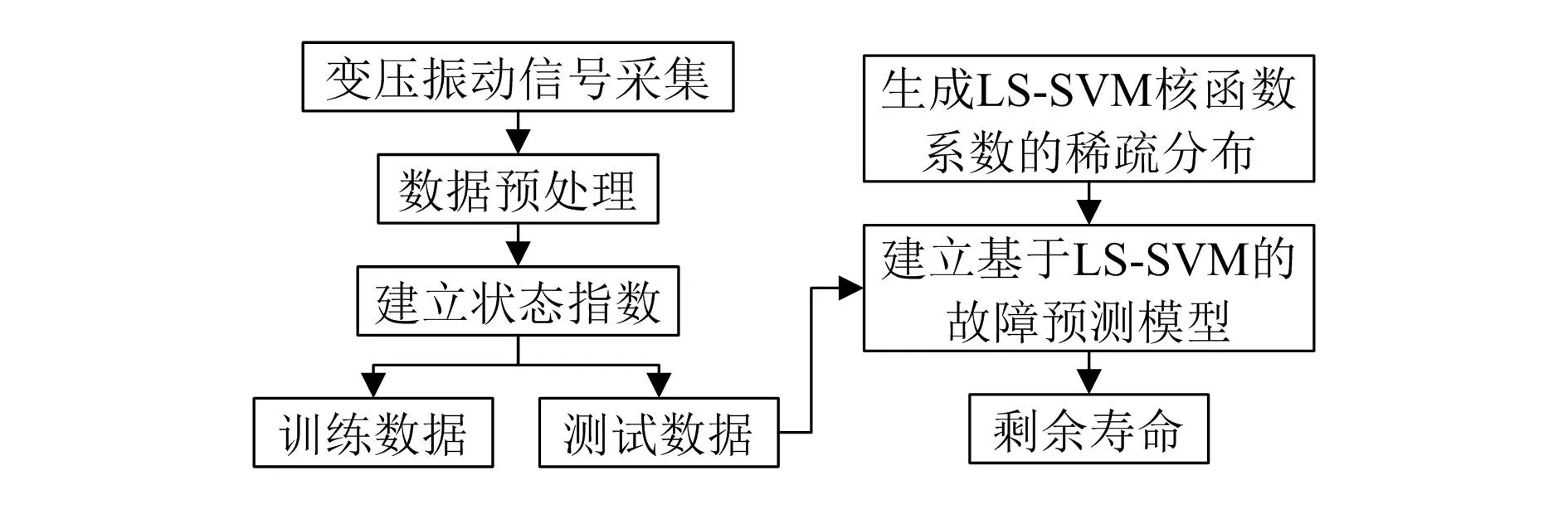
图3 变压器故障诊断流程

为测试变压器铁芯和绕组更换过程对模型测量精度的干扰程度,对不同条件下变压器高压C相进行扫频测试,变压器频率响应变化如图4所示。由图可以看出,拆卸变压器并更换铁芯和绕组后变压器的频率响应曲线无明显变化,即更换变压器铁芯与绕组未对本身结构造成影响,进一步表明诊断结果不会因铁芯和绕组的更换而发生变化。

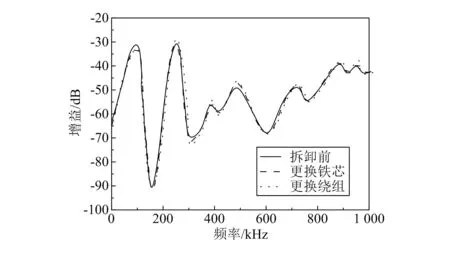
图4 变压器频率响应曲线

选择铁芯松动、铁芯形变、绕组松动以及绕组形变4种典型的机械故障类型进行预测;此外,对于混合故障需通过振动信号分别对绕组和铁芯的每一种故障进行诊断。对于故障诊断而言,需确定状态指数的失效阈值,为此,分别测试了故障发生时变压器铁芯及绕组对应的Hilbert边际谱图,如图5所示。根据变压器Hilbert边际谱图计算得到相应的失效阈值,见表1。可以看出,不同变压器组件的失效阈值有较大差异,主要是由于变压器铁芯与绕组二者间的故障机制和振动频谱存在较大差异,不同故障的表现并不一致。

图5 不同故障条件下变压器的Hilbert边际谱图

表1 不同故障下变压器组件的失效阈值

核函数系数通过量子遗传算法优化生成,分别测量4种故障类型1 200个时间节点数据,其中800个时间节点数据用于测试模型性能,400个时间节点数据用于训练LS-SVM模型。以10 kV铁芯形变为例,其诊断结果如图6所示。可以看出,优化生成LS-SVM模型的预测总谐波畸变(THD)值与真实THD值基本一致,进一步表明LS-SVM故障诊断模型能够准确预测变压器故障状态指数随时间的变化情况。

图6 10 kV铁芯形变总谐波畸变

故障预测中一般将剩余使用寿命(RUL)、相对误差(RA)和绝对误差(AE)作为预测效果评价指标。各实例中的诊断RUL、AE以及RA值见表2。可以看出,各个实例中的RA与AE均较小,其中实例6(110 kV三相变压器铁芯形变)的误差最大,其相对误差最大为2.67%;实例1(10 kV单相变压器铁芯松动)和实例7(110 kV三相变压器绕组松动)的误差最小,其相对误差仅为0.99%。上述结果证明LS-SVM算法能够有效增强变压器的检修指导,可以获取较为精确的故障发展趋势数据。

表2 各实例中的诊断RUL、AE以及RA值

为验证变压器故障诊断模型的泛化能力,对不同服役年限(2 a、4 a、6 a以及8 a)变压器进行故障预测,结果如图7所示。可以看出,训练样本数大于200时,故障诊断模型对服役年限为2 a和4 a的变压器的预测误差最小,主要是因为模型运行5 a的变压器运行数据为训练数据。而对于服役年限为6 a和8 a的变压器而言,模型的预测诊断误差依次增大,但均处于可接受范围内。

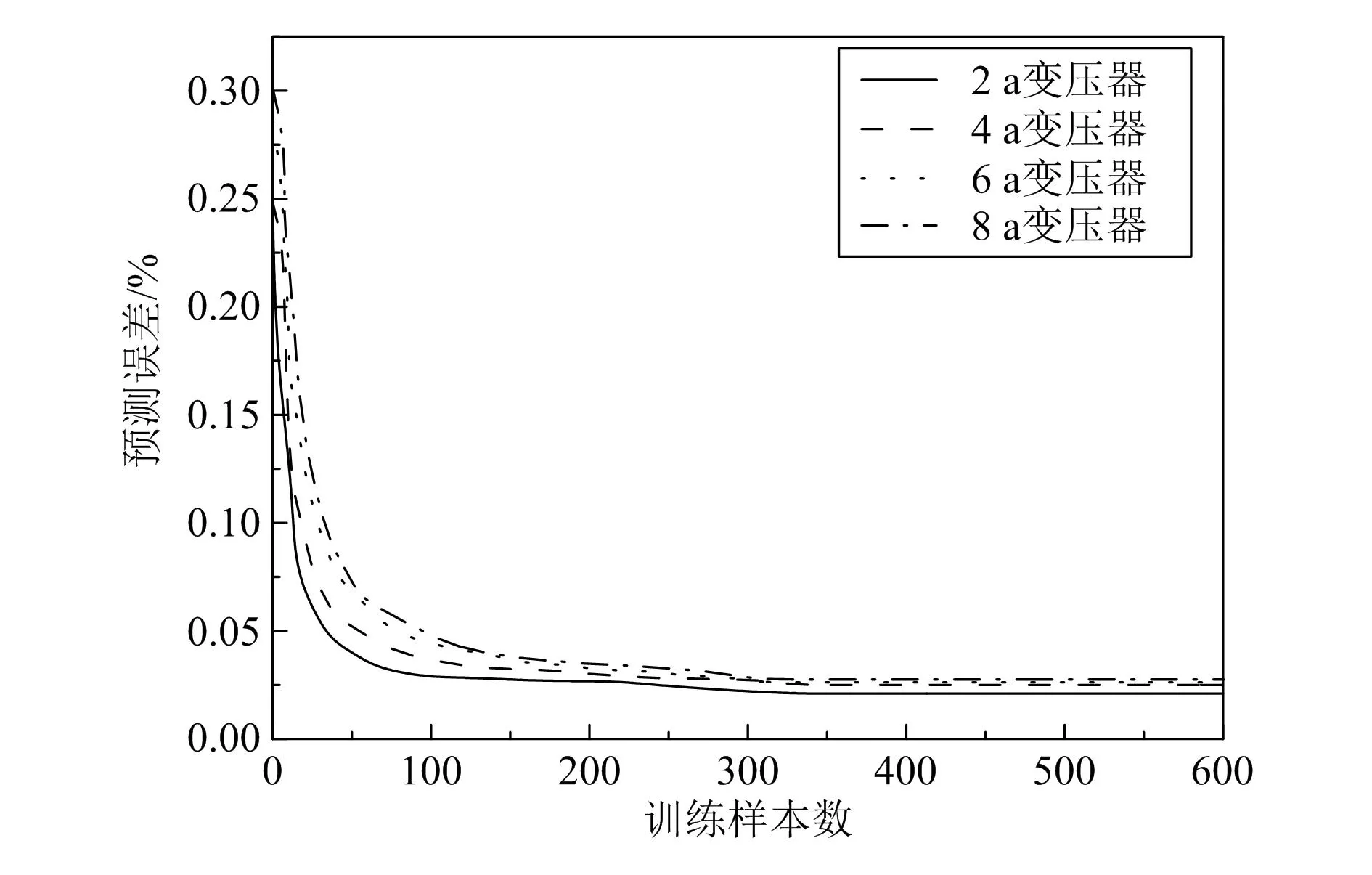
图7 不同服役年限变压器的预测结果

考虑到振动数据通过RFID传感器来进行采集和传输,可能会存在数据包误传输以及丢失的情况。不同误码率下模型预测精度如图8所示。可以看出,核函数明显提升了预测模型的泛化能力,当误码率小于0.01时,模型的预测误差低于0.05%,故障预测模型能够实现最佳的诊断精度;当误码率大于0.03时,模型预测误差将急剧上升,最高达0.40%。然而,正常工作时RFID系统误码率一般小于0.000 1,即模型能实现良好的预测性能。

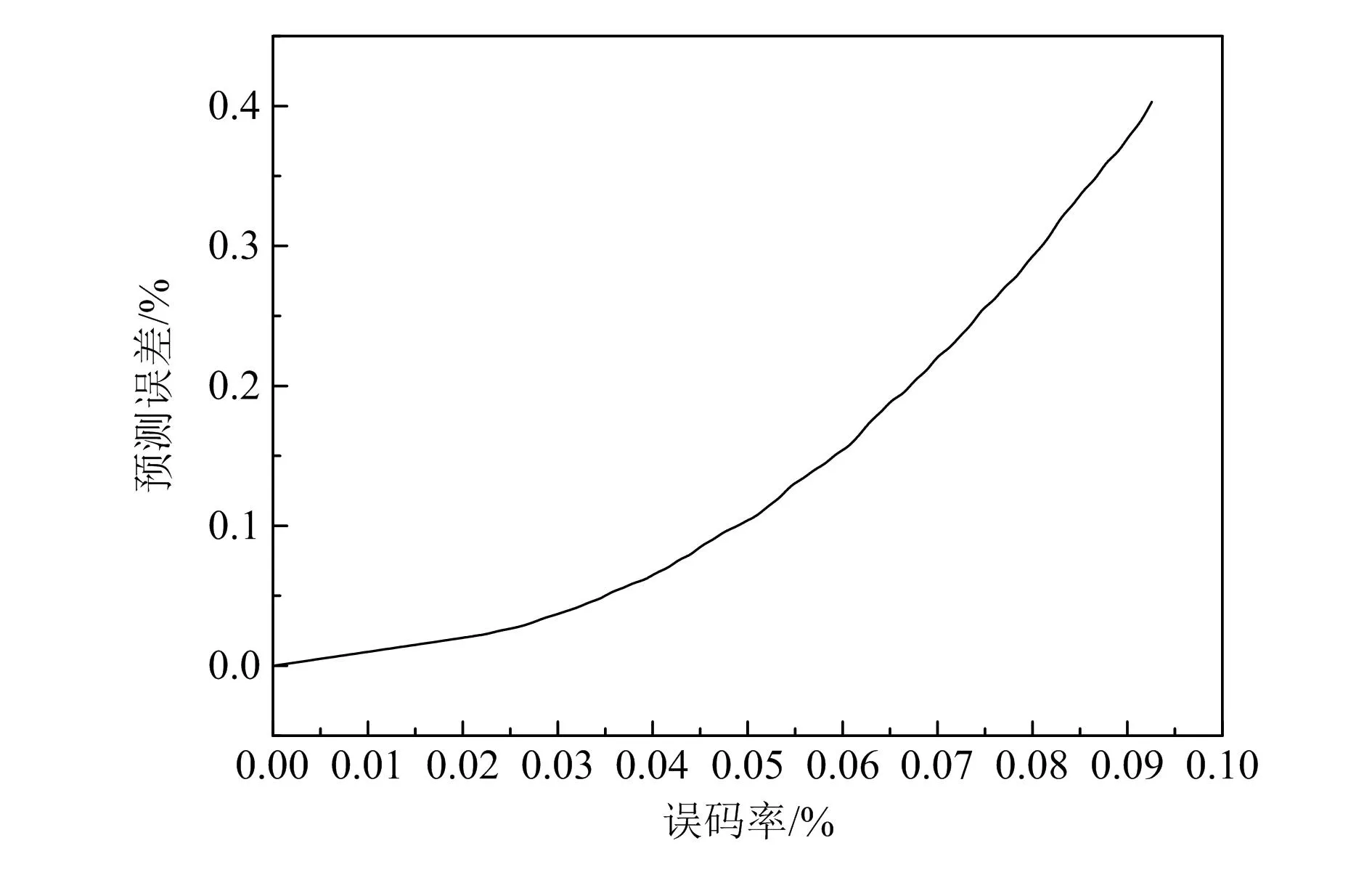
图8 不同误码率下的预测性能

3 结束语

本文从便利性与低成本的角度,设计了基于RFID的变压器振动信号采集和传输装置。并以Hilbert边际谱图为变压器故障特征参数,利用时频分析法对其振动信号进行采集和分析,研究表明:核函数可明显提升预测模型的泛化能力,当误码率小于0.01时,模型的预测误差低于0.05%,故障预测模型能够实现最佳的诊断精度;LS-SVM算法具有良好的泛化能力,能够精准预测铁芯及绕组机械故障的发展趋势。