用基本模型突破等腰三角形问题

王君

模型解读

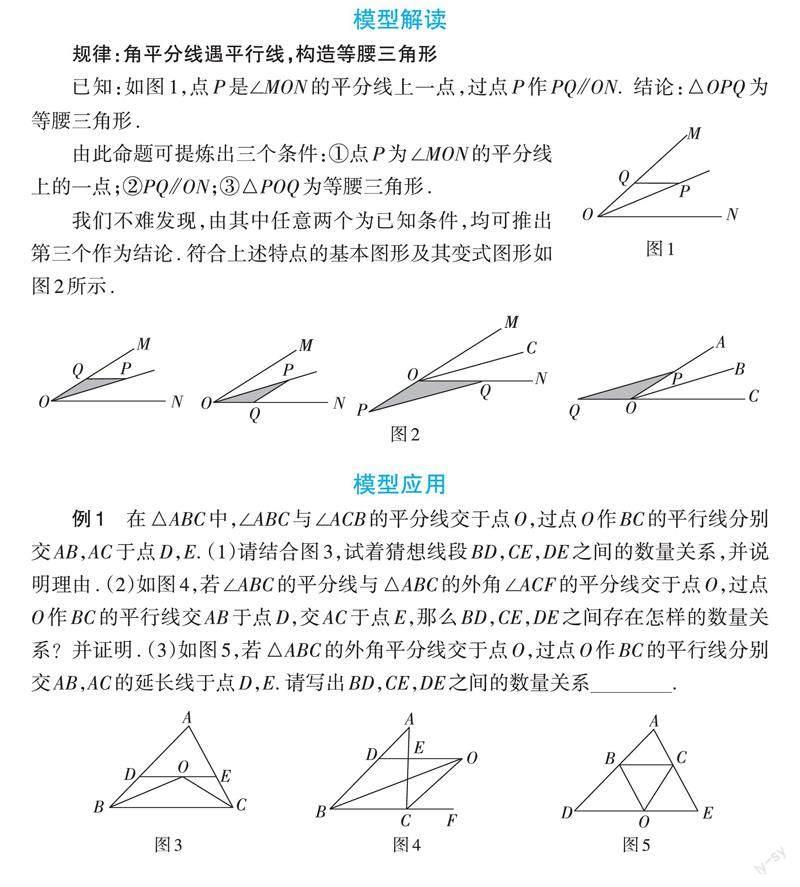
规律：角平分线遇平行线，构造等腰三角形

已知：如图1，点[P]是∠MON的平分线上一点，过点[P]作[PQ][?][ON].  结论：[△OPQ]为等腰三角形.

由此命题可提炼出三个条件：①点[P]为[∠MON]的平分线上的一点；②[PQ][?][ON]；③[△POQ]为等腰三角形.

我们不难发现，由其中任意两个为已知条件，均可推出第三个作为结论. 符合上述特点的基本图形及其变式图形如图2所示.

模型应用

例1 在[△ABC]中，[∠ABC]与[∠ACB]的平分线交于点[O]，过点[O]作[BC]的平行线分别交[AB]，[AC]于点[D]，[E]. （1）请结合图3，试着猜想线段[BD]，[CE]，[DE]之间的数量关系，并说明理由. （2）如图4，若[∠ABC]的平分线与[△ABC]的外角[∠ACF]的平分线交于点[O]，过点[O]作[BC]的平行线交[AB]于点[D]，交[AC]于点[E]，那么[BD]，[CE]，[DE]之间存在怎样的数量关系？并证明. （3）如图5，若[△ABC]的外角平分線交于点[O]，过点[O]作[BC]的平行线分别交[AB]，[AC]的延长线于点[D]，[E]. 请写出[BD]，[CE]，[DE]之间的数量关系.

解析：（1）如图3，由角平分线的定义得[∠DBO=∠OBC]，[∠ECO=∠BCO].

由平行线的性质得[∠DOB=∠OBC]，[∠EOC=∠BCO]，则[∠DOB=∠DBO]，[∠EOC=∠ECO]，[于是BD=DO]，[OE=CE]，从而[DE=BD+CE].

（2）如图4，同（1）得出，[BD=DO]，[OE=CE]，从而[DE=BD-CE].

（3）[DE=BD+CE.]

例2 如图6，在[△ABC]中，[∠ABC=30°]，[BD]是[∠ABC]的平分线，交[AC]于点[D]，[E]为[BD]上一点，过点[E]作[EF⊥AB]，交[AB]于点[F]，过点E作EG[?]BC，交AB于点G，若[EF=2]，求线段[BG]的长.

解析：[∵]EG[?]BC，[∴][∠GEB=∠EBC]，∠AGE = ∠ABC = 30°.

[∵][BD是∠ABC的平分线]，[∠ABC=30°]，

[∴][∠EBC=∠FBE=15°]，

[∴][∠FBE=∠GEB=15°]，[∴][BG=GE]，[∠FGE=30°].

[∵][EF⊥AB]，且[EF=2，][∴][GE=2EF=4]，[∴][BG=GE=4]，即线段[BG]的长为4.

分层作业

难度系数：★★解题时间：6分钟

1.如图7，[BA][?][DC]，点[E]在[BC]上，且[CD] = [CE]，[∠D=74°]，则[∠B]等于 .

2. 如图8，[∠MON=30°]，[OP]平分[∠MON]，过点[P]作[PQ][?][OM]，交[ON]于点[Q]. 若[OQ] = [4]，则点[P]到[OM]的距离为.

3. 如图9，在[△ABC]中，[AD]是[∠BAC]的平分线，[DE][?][AB]，交[AC]于点[E]，若[DE=7]，[CE=6]，则[AC]等于.

难度系数：★★★解题时间：6分钟

4. 如图10，把一张长方形的纸折叠，使得点[B]与点[D]重合，折痕为[EF]，那么△[BEF]是一个等腰三角形吗？为什么？

5. 如图11，在[△ABC]中，[AD]平分∠[BAC]，[BD⊥AD]，垂足为点[D]，过点[D]作[DE][?][AC]，交[AB]于点[E]，若[AB] = 5，求线段[DE]的长.