基于互斥锁传播的多智能体路径规划算法

岳荣康，丁 行，江 海，龙 吟

（1.西南科技大学 计算机科学与技术学院，四川 绵阳 621000；2.四川省烟草公司成都市公司，成都 610014）

0 概述

多智能体路径规划（Multi-Agent Pathfinding，MAPF）的目标是寻找出可使多个智能体无冲突地到达各自目的地的路径集合［1］。多智能体路径规划算法在诸多领域得到广泛应用，如智能仓库［2］、机场托运［3］、自主导引车、机器人［4］以及数字游戏［5］等。在多智能体路径规划应用中，最常见的目标是使得多个智能体能够以最短路径或者最短时间到达各自的目的地。然而，无论是寻找最短路径还是最短时间的方案，都是NP 难问题［6-7］。针对该问题，国内外学者在过去几年内已经取得了一定的进展，即使是在超过100 个智能体的场景中，也能有效地寻找出合适的解决方案。

大多数方案在解决最优化MAPF 问题时，都假设时间被离散化为时间步以及每个操作的持续时间均为一个时间步，这些简化假设削弱了多智能体路径规划算法在现实世界中的适用性［8］。本文的目标是解决一种更通用的多智能体路径规划问题，简称为MAPFR问题［9-10］。在MAPFR问题中，在连续时间线上的任意时刻智能体都占据了度量空间中的一个定义区 域。目前已 有算法（如E-ICTS［11］、ECBSCT［12］）解决了部分MAPFR问题，它们支持非均等时间成本的移动动作并考虑智能体占用的坐标区域。然而，这些算法仍然依赖于时间离散化来定义等待动作的持续时间，这可能会对解决方案的质量和运行时间产生负面影响［13］。最新提出的基于连续时间的冲突搜索（Continuous Conflict Base Search，CCBS）［14］算法虽然不依赖于时间离散化，但是它在面临基数冲突时会在上层搜索中扩展过多的约束树节点，继而导致算法的空间复杂度与时间复杂度存在一定的瓶颈。

本文提出一种优化算法以进一步解决MAPFR问题。使用一种人工智能规划领域中著名的互斥锁传播技术［15］，该技术是一种约束传播的形式，对应于有向一致性，而有向一致性又是路径一致性的截断形式。互斥锁传播技术与所有约束传播技术一样，能够高效地使隐式约束显式化。在人工智能规划中，互斥锁传播常应用于规划图，从而在多项式时间内紧密地近似从给定状态到达的所有可达状态的集合［16］，它已成功应用于设计状态空间规划器的可达性启发式算法［17］和计划空间规划器的启发式算法［18］中。规划图思想在多智能体路径规划研究中以多值决策图（Multi-valued Decision Diagram，MDD）［19］的形式出现。MDD 是为每个智能体而单独构建的，包含了它们的可达性信息［20］，但是，MDD 不包含智能体组合的可达性信息［21］。另一方面，直接为智能体组构建联合MDD 在计算上是不可行的，因为联合空间随着智能体数量的增加呈指数增长［22］。互斥锁传播技术在人工智能规划中缓解了上述困境［23］，本文将这种技术应用到多智能体路径规划研究中。在结合CBS 框架后，互斥锁传播能够有效识别基数冲突，在算法运行中能够取得更高的计算效率。现有工作只能在离散时间的假设下识别有限形式的基数冲突，并且需要手动设计对应的约束［24］，而互斥锁传播技术具有更强的迁移性，可以通过自动设计来打破对称性的约束，从而在运行时间和成功率方面提高CCBS 的冲突解决能力。

1 背景知识

1.1 多智能体路径规划问题定义

本文通过六元组〈Γ,M,S,G,coord,A〉来定义多智能体路径规划问题，其中：Γ=(V,E)是一个图；M是一个度量空间；S和G分别是起点和终点函数；coord 将Γ中的每个顶点映射到M中的一个坐标；A是有限移动动作的集合［15］。每个动作a∊A都由一个持续时间aD和一个运动函数aφ定义。运动函数aφ是一个将时间映射到度量空间的函数aφ：[0,aD]→M。当执行动作a时，aφ(t)是智能体在时间t处在M中的坐标。值得注意的是，这些运动函数的定义允许模拟以非常数速度移动并遵循任意几何曲线的智能体。

在MAPFR问题中有2 种类型的动作，即移动动作和等待动作。对于一个移动动作a∊A，限制aφ，使它从某个顶点v开始在另一个顶点v′结束，且(v,v′) 是E中的边，即存在v和v′，使 得aφ(0)=coord(v)，aφ(aD)=coord(v′)，(v,v′) ∊E。用from(a)和to(a)分别表示这些顶点。本文通过假设移动动作集合的有限性，将所提算法的完整性和最优性限制为仅与所选移动动作集合相关。如果一个算法在解决方案存在的前提下能够保证从一组移动动作集合A中返回一个有效的解决方案，则认为它对于移动动作集合A来说是完备的。在同样的移动动作集合A中，由不同动作组合而成的解决方案可以是非最优甚至是无效的。因此，如果一个算法能够保证它从移动动作集合A中返回的解决方案一定是所有有效方案中路径代价最小的，则认为它对于移动动作集合A来说是最优的。

对于等待动作a来说，存在一个顶点v∊V，使得对于每 个t∊[0,aD]，都 有aφ(t)=coord(v)。为了完整性，本文为等待动作定义from(a)和to(a)顶点。虽然移动动作的集合作为输入被给出，但是等待动作的集合对于每个顶点v∊V和任何正实数aD都是隐含定义的。因此，等待动作的集合是无限大的。当智能体在顶点v处时，它可以选择在v开始的任何动作，如移动或等待，即from(a)=v。如果智能体的形状重叠，则发生智能体之间的碰撞。为了检测这种重叠，本文设计如下不同于传统的碰撞检测方法公式：

当智能体i和j分别占据位置mi和mj时，它们的形状重叠时IsCollision(i,j,mi,mj)=true。例如，如果智能体是二维盘状且半径为r，则当智能体之间的距离小于2r时会发生碰撞。也就是说，在这种情况下，可以使用IsCollision(i,j,mi,mj)=dist(mi,mj) <2r来检测智能体之间的碰撞，公式表达如下：

对于一个动作序列π=(a1,a2,…,an)，这里采用π[：j]表示前j个动作，π[：j]=(a1,a2,…,aj)。π的持续时间和运动函数分别称为πD和πφ，它们的定义如下：

式（3）计算在执行π时每个时刻的位置，需要注意的是，运动函数是相对于相对时间而不是绝对时间定义的。例如，对于将智能体从v移动到v'的任何动 作a，有aφ(0)=v和aφ(aD)=v'。因 此，为了计 算πφ(t)，需要先确定在时间t计划执行的动作。可以通过观察π中的第i个动作从(π[：i-1])D的时间开始、在(π[：i])D的时间结束来计算。然后，通过该动作的开始时间校正t，以获得智能体在该动作执行期间的位置。式（3）的最后一行定义了在计划结束后智能体保持在其最后一个位置。

MAPFR与经典多车路径规划问题一样，本文将单智能体的计划定义为一个动作序列π=(a1,a2,…,an)，执行该序列会使智能体i从si移动到个单智能体计划之间的冲突定义为：当2 个智能体同时执行各自的计划时，则在某个时间点发生碰撞。

定义12 个智能体的路径规划有冲突，则有：

∃t∊[0,max(πiD,πjD)]，IsCollision(i,j,πiφ(t),πjφ(t))

当一个智能体的计划路径与其他智能体的路径都不构成冲突时，则认为它的计划路径是有效的。单智能体的计划路径代价就是其持续时间，与经典多车路径规划问题类似，计划路径的代价总和是单一智能体计划成本总和，而计划路径的完成时间是这些路径代价的最大值。

1.2 基于冲突的搜索算法

CBS 是一个具有两层结构的多智能体寻路算法。在CBS 的上层算法中维护着一棵约束树，树中每一个节点包含了约束和满足该节点所有约束的路径［17］。CBS 的下层算法则是针对单智能体的寻路算法，它的任务是为每一个智能体找到满足当前约束树节点中所有约束的最短路径，通过它得到的路径只考虑了约束，未将其他智能体的影响纳入计算范围内，因此，生成的路径之间很可能存在顶点冲突或者边沿冲突。当搜索完成后，若现有节点中的路径集合无冲突，则会返回这个路径集合作为最终的解；当路径集合中存在冲突时，CBS 上层算法会选择一个冲突扩展子节点，并为产生冲突的2 个智能体添加约束，直到找到无冲突的路径集合为止。

根据文献［18］的定义，CBS 算法中的冲突可以分为3 类，当2 个智能体分别满足当前约束树节点的约束后，有以下3 种情况：1）智能体ai和aj都无法找到小于等于路径代价为li和lj的无冲突路径对，则称它们之间的冲突是重要冲突；2）次要冲突意味着2 个智能体中有且仅有1 个智能体可以找到使得彼此无冲突的路径；3）一般冲突则是指2 个智能体均可找到无冲突的路径。

1.3 基于动作序列的多值决策图

在多智能体路径规划中，传统的多值决策图是由离散的时间步表示的层级关系及节点坐标顶点而构成的［19］，无法直接应用于连续时间下的多智能体路径规划问题。本文将传统地图中的边替换为智能体实际执行的动作，并添加相应的动作执行时间窗。

在本文所提出的多值决策图中，每个节点拥有level、time 和loc 属性，level 代表在该智能体当前的动作规划中到达该节点对应loc 的序列，time 则是到达对应loc 并停留的时间。每条边还额外带有执行时间窗，代表这条边对应动作的开始执行时间与结束时间。

1.4 基于规划图的互斥锁传播

规划图一般包含命题节点和动作节点这2 种类型的节点，这些节点按级别划分，偶数级别只包含命题节点，奇数级别只包含动作节点，零级别表示起始状态。如果命题是下一级动作的先决条件，则命题节点与动作节点之间会连接一条边。此外，如果命题由该动作变成真，则动作节点与命题节点之间也会连接一条边［20］。规划图表示并行动作的效果，但这种方法非常粗略。为了更好地近似可达状态集，使用以下规则在规划图上进行互斥传播。

在第i层，如果2 个动作节点互斥，则满足以下条件：1）一个动作的效果为另一个动作效果的否定；2）一个动作删除了另一个动作的先决条件；3）一个动作的先决条件和另一个动作的先决条件在第i-1层互斥。如果2 个命题节点互斥，则满足以下条件：1）一个命题是另一个命题的否定；2）第i-1 层中实现一个命题的所有动作与第i-1 层中实现另一个命题的所有动作之间均为互斥。

在多智能体路径规划的背景下，MDD 是一种有向的分层数据结构，类似于规划图。但是，由于每个智能体在执行动作时都可以在当前顶点u处等待或者经过边，因此每个动作都有一个前提条件，即智能体在该动作开始执行时处于顶点u。因此，无需显式表示动作层，为每个智能体单独构建的MDD集合可以看作是规划图的特殊情况。同样地，在MDD 中，互斥锁传播规则也可以简化。如果MDDi中 的MDD 节 点ni和MDDj中 的MDD 节 点nj在t层是互斥的，则不存在冲突的子路径，该子路径将智能体ai和aj从其在时间步0 处的起始顶点移动到时间步t处的顶点ni.loc 和nj.loc。由于互斥传播可以在多项式时间内进行，因此可以有效且紧密地近似可达顶点集，从而获得有用的信息。

2 互斥锁传播在多值决策图中的应用

本文根据多值决策图的构成定义了2 种初始互斥锁，分别是节点互斥锁与边沿互斥锁。在一组多值决策图中，2 个节点(ni.time ∩nj.time)≠∅且ni.loc=nj.loc，则认定它们是一对节点互斥锁。类似地，在一组多值决策图中，2 条边同时满足(ei.time ∩ej.time)≠∅、ei.from.loc=ej.to.loc 和ei.to.loc=ej.from.loc 时，则认为它们是一对边沿互斥锁。

例如，图1 所示为4 种基数冲突，图2 中展示了智能体a1和a2陷入图1（a）所示的矩形冲突时的一组多值决策图。多值决策图中节点的标签代表其所对应的地址坐标，虚线连接的一对节点指它们互为节点互斥锁。在第1 层，MDD1的B2 与MDD2的B2 就明显是一对节点互斥锁，代表的实际意义是2 个智能体可能在第1 个动作执行完成后在坐标B2 处陷入冲突。

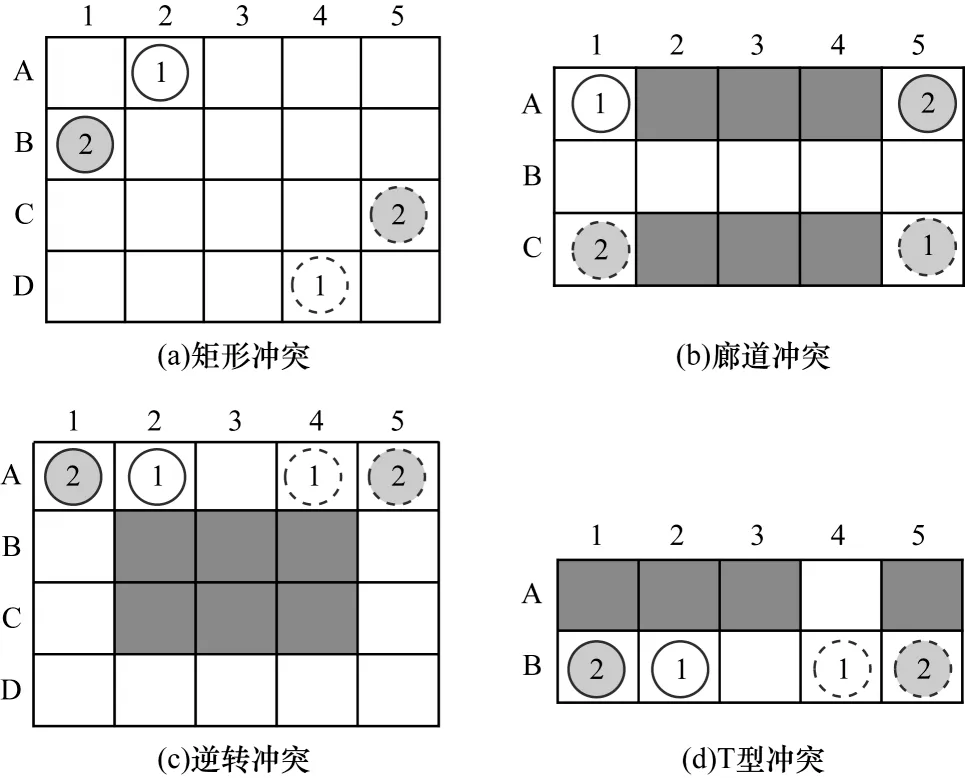
图1 基数冲突Fig.1 Cardinality conflict

图2 位于图1（a）中的2 个智能体对应的MDDFig.2 The MDD corresponding to the two agents in Fig.1（a）

基于互斥锁的传播特性，本文定义2 种传播互斥锁在多值决策图中的传播方法，分别是基于节点的前馈传播和基于边的前馈传播。在基于节点的前馈传播中，当2 个节点(ni.time ∩nj.time)≠∅且图中所有满足ei.to=ni和ej.to=nj的边构成边沿互斥锁时，2 个节点构成传播互斥锁。在基于边的前馈传播中，当2 条边(ei.time ∩ej.time)≠∅且ei.from 和ej.from 互为互斥锁时，则这2 条边构成传播互斥锁。

例如，图2 中实线连接的节点都是传播节点互斥锁。很明显可以知道，MDD1的B2 与MDD2的B2就是一对初始节点互斥锁，因此，MDD1中B2 到C2的边与MDD2中B2 到B3 的边是一组传播互斥锁。在第2 层，2 个MDD 中都只有1 条边可以前往MDD1中 的C2 和MDD2中 的B3，正 是MDD1中 的B2 到C2以及MDD2中的B2 到B3。因此，MDD1中的C2 和MDD2中的B3 构成传播互斥锁，使用实线连接。

本文采用算法1 在一对MDD 中识别出初始互斥锁与传播互斥锁，该算法类似于AC-3 算法。值得注意的是，这里的算法流程仅用于阐释整个算法的核心想法，看起来可能效率略有不足。首先将所有的初始互斥锁加入队列中，然后逐一判断所有互斥锁能否向后传播。传播互斥锁形成后也会加入队列中，在MDD 的每一层总是先检测节点的互斥关系再检测边的互斥关系。

算法1互斥锁的生成

推论1如果MDDi中的ni与MDDj中的nj是一对互斥锁，且有ni.level=nj.level=l，那么对于2 个智能体ai和aj，不存在一对可用的路径pi与pj。具体来说，这对路径的起始时间是0，起点分别是si与sj，且它们会在时间l分别到达ni与nj。

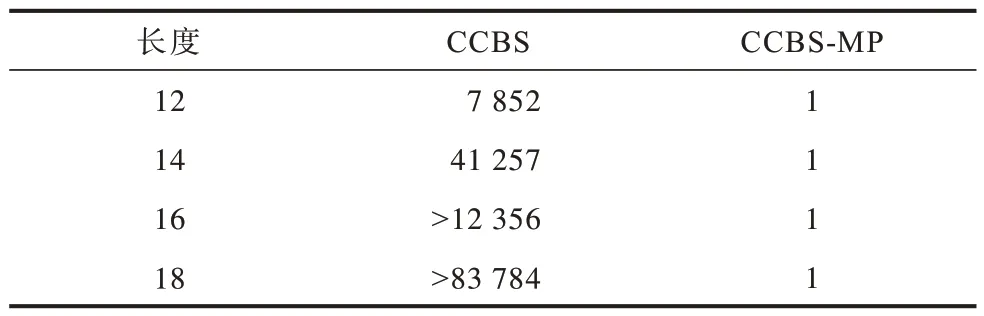
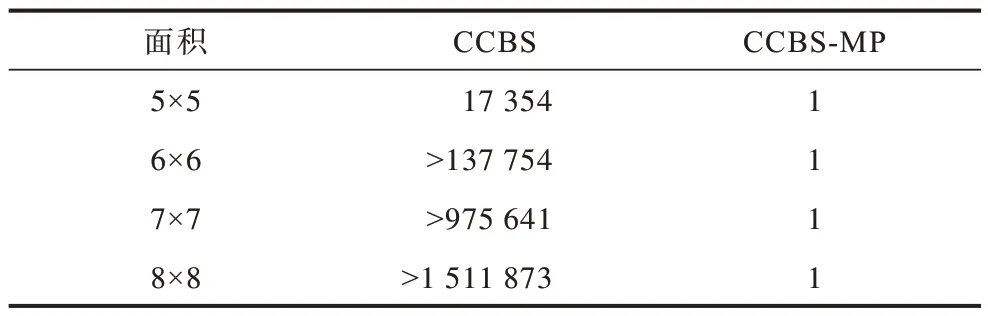
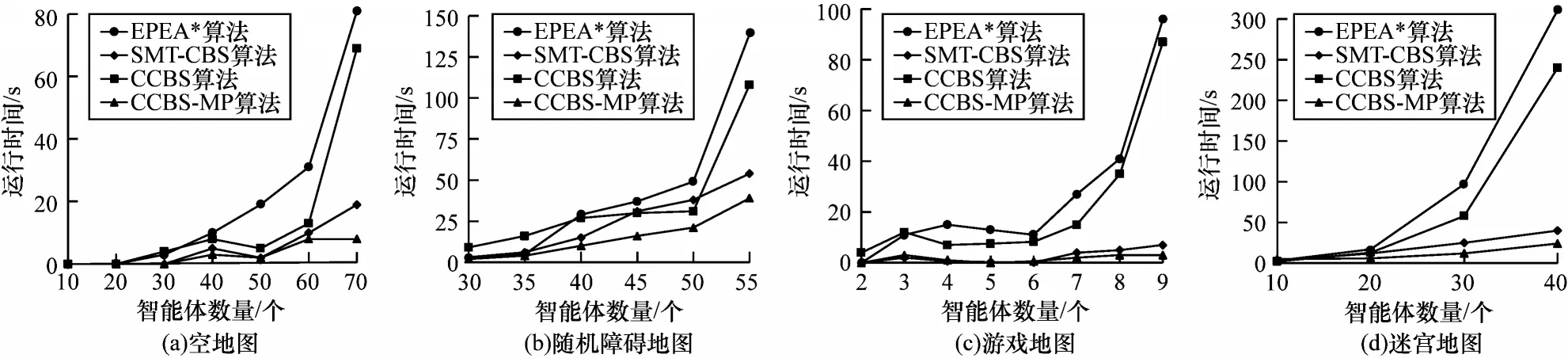
证明当ni与nj是一对初始互斥锁时，结论则显而易见。因此，本文着重论述当ni与nj是一对传播互斥锁的情况，假设此时存在一对这样的可用路径pi与pj且是无冲突的，定义ni,t表示pi中时间t时智能体ai所对应的到达节点ni，nj,t表示pj中时间t时智能体aj所对应的到达节点nj。由定义有ni,0.loc=si，nj,0.loc=sj，ni,l=ni，nj,l=nj。通过互斥锁的定义，接下来证明ni与nj不是一对传播互斥锁。首先，可以知道si≠sj，因 此，ni,0与nj,0一定不 构成互斥锁，又因为此时存在一对可用路径pi与pj，所以可以知道在t

推论2如果MDDi中的ni与MDDj中的nj满足ni.level=nj.level，但不构成互斥锁，那么一定存在一对可用路径pi与pj，使得智能体ai和aj可以在时间l时无冲突地到达ni与nj。

证明因为ni与nj不构成互斥锁，所以一定存在一组终节点是ni与nj的边不构成互斥锁。因此，不断反馈传播可以一直推到智能体ai和aj的起点si与sj，则传播得到的路径就是这一对可用路径pi与pj。

综合推论1 与推论2，可以得到引理1。

引理1当且仅当MDDi中的ni与MDDj中的nj满足ni.level=nj.level 且不构成互斥锁时，存在一对可用路径pi与pj，使得智能体ai和aj可以在时间l时无冲突地到达ni与nj。

3 基于互斥锁传播的基数冲突识别

在实践中可以得知不同智能体的路径长度并不总是等长的，因此，很可能出现智能体ai已经到达目的地并始终停留在gi处而智能体aj与之产生冲突的情况。针对智能体之间的可能冲突发生在智能体到达目的地之前，以及发生在其中一个智能体到达目的地之后的2 种情况，互斥锁传播需要不同的方式来进行处理。本文将这2 种冲突区分开来，并在后续做出不同处理。

终点前基数冲突（Pre-goal Conflict，PC）指不考虑智能体会在终点停留这一假设时，仍然无法在现有的一组MDD 中找出一对可用路径，使得智能体ai和aj能够无冲突地到达各自目的地。与之相对应的是终点后基数冲突（After-goal Conflict，AC），代表在给定的运动时长范围内，存在一组可用路径，可以使得2 个智能体无冲突地到达各自的目的地，但是无论哪一组可用路径，总是会在另一智能体到达目的地后穿过其目的地。

算法2基数冲突的识别

引理2当且仅当算法2 返回非基数冲突时，中存在一对路径代价分别为li与lj的可用子路径pi与pj。

证明 假设此时存在一对可用路径pi与pj，通过引理1 可以知道中第li层存在一个节点nj与的终节点不构成互斥锁，又因为路径pi与pj是无冲突的，所以智能体aj在li时间后不会穿过智能体ai的目标节点gi。综上，此时存在一条从nj到gj的可用路径，且其不会穿过智能体ai的目标节点gi，此时算法2 会返回冲突种类为非基数冲突。假设算法2返回非基数冲突，容易知道中存在一条路径p可从nj到达终节点，并且中途不会穿过的终节点gi。通过引理1 可以得知，存在一对可用路径pi与pj可使智能体ai和aj从起点移到gi与nj。如果智能体ai到达gi后一直停留在gi处，那么pj结合路径p即可构成一条使得智能体aj从sj移动到gj且与pi无冲突的路径。

综上所述，当且仅当算法2 返回的冲突类型为终点前基数冲突或终点后基数冲突时，智能体ai和aj之间存在基数冲突。

4 基于互斥锁传播的基数冲突解决

本文提出2 种用于生成约束集合的算法，分别用来解决终点前基数冲突与终点后基数冲突。

推论3当冲突类型是终点前基数冲突时，如果智能体ai的路径pi违背约束集合Ci以及智能体aj的路径pj违背约束集合Cj，那么路径pi与pj一定存在冲突。

推论4当冲突类型是终点后基数冲突时，如果智能体ai的路径pi短于代价约束的限制，且智能体aj的路径pj违背了约束集合Ci，那么路径pi与pj一定存在冲突。

证明约束集合Cj中包含了第li层中与的终节点构成互斥锁的节点以及中大于li层但满足n.loc=gi的节点。如果智能体aj违背了约束集合Cj，那么它一定会与停留在gi处的智能体ai产生冲突。通过引理1 可知，此时智能体ai和aj对应的路径pi与pj一定存在冲突。

5 实验结果分析

将CCBS 与互斥锁传播(Mutex Propagation)相结合的方法简称为CCBS-MP。首先将CCBS-MP 与CCBS 在图1 所示的基数冲突实例上进行比较，然后列出在不同栅格地图环境下CCBS-MP 与CBS 框架中现有最前沿算法CCBS、SMT-CBS 以及A*算法中最前沿版本EPEA*的性能对比。在实验中，除了冲突分类和约束生成之外，3 种算法采用相同的代码库。本文在亚马逊云服务器中选用内存为8 GB 的EC2 虚拟机进行所有实验。

5.1 基数冲突

本文在图1 中给出了基数冲突的一些实例。表1～表3 分别显示了CCBS-MP 和CCBS 算法在不同类型冲突中运行时的约束树节点展开数。表中的前缀“>”表示求解器在5 min 内未能解决该实例，“>”后面的数字表示运行时限到达时的约束树节点展开数。从中可以看出，CCBS-MP 在1 s 内就能解决所有实例。

表1 在不同长度的对称冲突下约束树节点生成数量对比Table 1 Comparison of the number of constraint tree nodes generated under symmetric conflicts of different lengths

表2 在不同面积的基数冲突下约束树节点生成数量对比Table 2 Comparison of the number of constraint tree nodes generated under cardinality conflicts of different areas

表3 在不同面积的非基数冲突下约束树节点生成数量对比Table 3 Comparison of the number of constraint tree nodes generated under non cardinality conflicts of different areas

由于缺少对应的规则生成具有针对性的约束，CCBS 不能有效地解决基数冲突。对于矩形冲突、走廊冲突和目标顶点冲突，CCBS-MP 在找到最优解之前仅展开1 个约束树节点；对于交换冲突，CCBS-MP在约束树底部仅展开3 个具有基数冲突的约束树节点，而在约束树的其余部分仅展开具有半基数和非基数冲突的约束树节点。

5.2 基准环境

本文使用文献［15］提供的4 个基准地图，包括如下：

1）2 个小地图，分别是16×16 的空地图和拥有20%随机障碍的32×32 地图。

2）2 个大地 图，分别是194×194 的游戏 地图和128×128 的迷宫地图，走廊宽度均为1［25］。

为了测试算法的求解极限，本文改变智能体的数量进行对比，对于不同的智能体数量，统计基准集中25 个不同场景下的平均成功率，将其作为最终的实验结果之一。

图3 显示了CCBS-MP、CCBS、EPEA*［26］和SMT-CBS的成功率，分别统计它们在5 min 的时间限制内解决的实例数。图4 显示了每个求解器在所有已解决的实例上的平均运行时间。从中可以看出：在16×16的空地图中有许多基数冲突，CCBS-MP 和SMTCBS 的效果都优于CCBS；在其他3 种环境更为复杂的地图中，CCBS-MP 在运行时间和成功率方面均优于CCBS 和SMT-CBS。同时，可以观察到EPEA*算法在环境较为简单的空地图中与CCBS 算法表现相当，而在较为复杂的地图环境中且智能体数目较多时，EPEA*会出现成功率与运行时间性能急剧降低的情况，这主要是由于EPEA*算法空间复杂度过高，受限于实验设备的内存空间，从而导致这样剧烈的性能变化。针对CBS 框架中的算法，CCBS 无法识别出基数冲突与对称冲突，且没有生成对应的特殊约束，而SMT-CBS 在矩形冲突之外没有更多的规则来应对基数冲突。在CBS 算法框架中，无法提前识别出基数冲突，导致的直接结果是过多地扩展约束树节点，既延长了无冲突路径集合的计算时间还占用了内存空间，每扩展一个约束树节点，不仅需要下层算法重新根据约束规划最优路径，还需要上层算法重新检测新路径组合中可能存在的冲突。

图3 4 种场景下的算法成功率对比结果Fig.3 Comparison results of algorithms success rates in four scenarios

图4 4 种场景下的算法运行时间对比结果Fig.4 Comparison results of algorithms runtime in four scenarios

6 结束语

互斥锁传播技术可以有效推理2 个智能体之间的相互作用并从产生的互斥中推断可应用的约束。基于互斥锁传播技术，本文提出一种新的算法框架，用于自动识别基数冲突并生成强约束集以对约束树进行分支，同时保证CBS 的最优性与完备性。实验结果表明，与目前前沿的MAPF 求解器相比，该算法的运行时间和成功率有一定优势。下一步将利用互斥锁传播技术来解决半基数冲突和非基数冲突，同时在MAPF 的不完整布尔模型中使用互斥锁传播技术。