面向汽车充电预约的光储充电站能量调度策略

赵文薇，林 兵，2，卢 宇，，王明芬

（1.福建师范大学 物理与能源学院，福州 350117；2.北京大学 信息科学技术学院，北京 100871；3.福建师范大学 协和学院，福州 350117）

0 概述

2019 年全球一次能源利用中，84%来自化石能源［1］。中国是世界最大的能源生产国和消费国，2020 年碳排放占全球碳排放总量的31%，居第1 位［2］。而汽车，是交通领域二氧化碳的主要排放源。新能源电动汽车（Electric Vehicle，EV）的普及可以有效减少二氧化碳排放，降低碳污染和汽车的运行成本［3］。汽车电动化无疑是交通领域实现“碳达峰、碳中和”目标的主要路径［4］。

推进EV 推广普及的关键因素是其充电的便捷性。目前，公认最具应用前景的解决方案是EV 的能源补给基础设施——光储充电站（Photovoltaic Storage Charging Station，PSCS）的合理 化部署［5］。大量EV 的不协调充电行为可能对电力质量和电网整体稳定性构成重大冲击，形成高峰，降低储备利润，扰乱供需，影响电压［6］。同时，随着以光伏（Photovoltaic，PV）、风电为主要形式的分布式能源和储能技术的快速发展［7］，带储能系统（Energy Storage System，ESS）的PSCS［8］为应用调峰和需求响应策略提供了可能，能够实现分布式能源、储能、智能充电相互协调支撑的绿色运行模式。

PSCS 在满足EV 负荷需求的同时，通过合理吐纳PV，控制储能系统在负荷低谷时间片充电，在较高的销售价格下实现多余能源到电网，以降低需求侧峰谷差、提高电力供需平衡，达到降低成本、安全运行的目的。为了描述这种动态调度，系统内供应和需求之间的能量交互可以建模为能量管理模型。针对能量管理，ALUISIO 等［9］对EV 日常运行和PV产量预测的运营成本进行了研究，提出了种供EV 的直流微电网运行优化规划的方法。DICORATO等［10］考虑模块化电动汽车供应基础设施的结构，进行协调控制及设计双向充电功能，但没有考虑EV 充电规划。RAFIQUE 等［11］提出一种基于实编码GA 算法的优化模型来优化能源的调度。作为凸规划问题，YAN 等［12］考虑EV 充电需求、PV 的不确定性，使用随机规划模型，但对EV 充电规划没有进行具体研究。LUO 等［13］重点从多类型充电设施出发考虑其年社会成本，建立了混合整数二阶段规划优化问题。BIYA 等［14］采用基于最大功率跟踪、PID 和电流控制策略的充电站设计方法，实现分布能量管理。YAN 等［15］考虑PV 发电和充电需求的不确定性，但同样没有考虑细化充电规划。ZHENG 等［16］重点研究了配电网潮流和母线电压约束的多电动汽车充电站在线最优充电策略，但未考虑需求端充电规划。曹凌捷［17］针对目前充电站负荷高峰与电源出力不匹配的特点，重点分析如何对系统中的供电侧进行能量管理。陈理宁等［18］兼顾PV 出力、电动汽车充电功率及储能充放电状态，采用多目标帕累托优化模型，并采用NSGA-Ⅱ算法进行求解。张丽娜等［19］构建以系统总运行成本最小为目标的优化模型，用粒子群优化算法进行求解。禹威威等［20］综合多因素构建了在分时电价和需求侧响应机制下的多目标优化模型，使用非支配排序遗传算法进行优化求解。王守相等［21］建立了提升配电网灵活性的两阶段优化模型，构建了基于蒙特卡洛树搜索的EV 有序充电模型，采用粒子群优化算法进行优化求解。SARKER 等［22］考虑储能系统的损耗成本、EV 的随机能源需求以及储能调度的鲁棒性，提出集群管理框架，以最小化EV 充电站运营成本。陈刚等［23］针对系统分散分布的特点，考虑储能电池的寿命损耗成本，提出基于多智能体一致性算法的储能单元分布式协同控制策略。LUO 等［24］采用随机动态规划和贪婪算法计算充分充电价格。郝越等［25］对于调度模型采用GA 对以单日利润最大为目标函数进行求解。江宏玲等［26］考虑储能系统的购电成本和未来一段时间的运行收益，但未考虑需求端充电规划。

目前关于PSCS 的能量管理研究较多，其中部分针对EV 需求侧进行优化调度，也有一些针对PV 产量预测和系统约束优化，相比，较少学者在能量优化过程中针对充电规划进行优化调度，关于需求端和能源端前后配合的优化工作也比较少。因此，考虑到今后大规模的充电需求和时间约束，在满足EV 充电需求的情况下，实现预约机制下PSCS 的EV 充电负荷调度和能量管理愈发重要。

基于上述研究现状，本文对储能系统调度和充电策略展开研究，本文研究通过PSCS 系统模型，考虑预约车辆充电的时机、功率调配和能量调度，以充电形式和能源调配的协作来实现能量调度的流动性。此外，提出基于带精英策略的遗传算法的混合递推优化策略（Elitist Genetic Algorithm Hybrid Recursive，EGAHR），即一种在PSCS 系统中考虑充电规划的能量调度优化的机制。采用贪婪决策方法对系统能源进行调度，满足EV 的充电要求，并最小化电网侧成本。同时，EGAHR 策略利用最佳拟合的思想来优化调度，以保证系统可以找到最佳能量调度策略。最后，基于PSCS 历史数据和数据集，通过模拟不同系统配置下的能量调度和效果变化进行仿真实验，验证EGAHR 策略的效果。

1 系统模型和问题定义

PSCS 系统主要包含电网、ESS、PV、负荷单元和其他电子设备。负荷单元包含基础负荷和EV 充电负荷，可由PV、ESS 和电网协同供电。作为充电负荷的输入口，充电桩为EV 提供充电服务，同时收集EV 充电信息。

图1 是PSCS 系统架构，由图1 可知，电网和ESS通过AC-DC 转换器接入，PV 通过DC-DC 转换器连接到母线。能量管理系统（Energy Management System，EMS）内部基于EGAHR 算法设定能量调度策略。为了确保EV 充电的服务质量，假设每阶段EV 数不大于充电桩数。

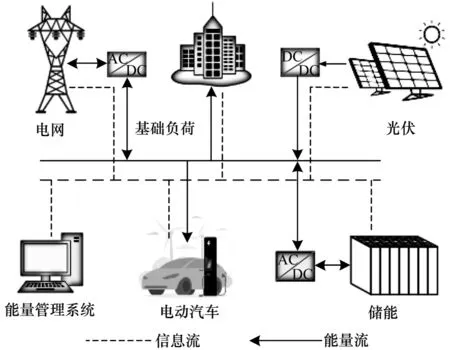
图1 PSCS 系统架构Fig.1 Architecture of PSCS system

图2 进一步展示了PSCS 系统能量流调度细节。在PSCS 系统的日常运行中，EMS 系统获取PV 发电、储能状态、EP、EV 等相关信息，并管理所有EV 的充电过程，实现充电能源的调度策略制定。PV 输出优先服务需求负荷，过剩能量存储到ESS 或反馈到电网。当PV 输出不能满足负荷需求时，则由电网或ESS 来供给。ESS 的关键作用是在低EP 时期存储电网电力或多余的PV 发电，并在高EP 时放电，利用峰谷差进一步减少成本。为避免PV 波动性的影响，上述运行假设PV 已知，而考虑充电规划的能量调度策略和算法，将在下一节介绍。

图2 PSCS 系统的能量流调度Fig.2 Energy flow scheduling for PSCS system

图3 EV 充电时段关系示意图Fig.3 Schematic diagram of EV charging time relationship

1.1 EV 预约充电模型

EMS 系统根据EV 预约信息（充电需求、到达时间和离开时间），在合适的时间以合适的充电模式来选择合适能源充电，达到削峰填谷目的的同时，降低车主充电费用和运营商的成本。假设：EV 离开前的荷电状态（State of Charge，SOC）达到100%，为简化实际模型，忽略EV 和储能中电池的效率和寿命造成的成本影响。

EV 的充电模式分快充P1和慢充P2两种，同时采取智充策略。若平行充电车辆过多导致用电紧张，达到上限而采取错峰供电，则阶段性调节慢充为第3 种零功率P0充电。EVi的停车时间和充电需求分别表示为tp,i和Ro,i，快充和慢充的充电时间分别由t1和t2表示，充电桩的输出功率决定于停车时间和满足需求用快慢充电方式所用时间的关系。当一段时间需求能量负荷达到最大限制时，使充电设施被饱和占用或EV 充电时间过少等情况统称为其他状态。充电功率的表达式如式（1）所示：

对于慢充的EV，EMS 系统可以通过间断控制将充电时间调整到低EP 时间片。对于快充的EV，一旦开始充电，过程将不会中断，EMS 在优化调度中只需要确定何时开始充电即可。

1.2 需求计算

对于EVi，本文假设EV 的充电完成时间可以早于其断开时间，但不能超过用户定义的断开时间。EV 停车时间和充电时间关系的示意图如图4所示。

图4 EV 停车时间和充电时间关系的示意图Fig.4 Schematic diagram of relationship between parking time and charging time of EV

设I表示整个期间预约充电EV 的预期总量。本文用I×T的逻辑矩阵W（0-1）记录在不同时间片EV的充电状态，如图5 所示是EV 充电状态示意图。有如下EV 充电状态的二元变量wi,t：

图5 EV 充电状态示意图Fig.5 Schematic diagram of EV charging state

其中：[Ai,Di]表示EVi的接入时间片范围；nc,i表示EVi完成充电任务的时间片个数。nc,i的计算过程为：

此时，考虑到包括空调散热、设备运转等的基础负荷Lbase,t，在t时间片用电总负荷PEVA,t为：

其中：PEV,t表示t时间片的EV 负荷，通常情况下，由于EV 预约信息的差异性，智充策略的充电决策受直接影响。

1.3 能量供应模型

为满足EV 的充电需求，在PSCS 内部由能源相互调度供应。因此，根据功率守恒约束，在t时间片内本文有：

其中：PEVA,t表示包含EV 负载的总负荷；PESS,EVA,t表示由ESS 供电；PPV,EVA,t表示 由PV 供电；PGrid,EVA,t表示由电网供电。

1.3.1 ESS 模型

设SSOC,t为ESS 在t时间片的荷电状态，其范围为0～1，可由ESS 在t时间片的剩余电量ERem,t和总容量ETotal来计算，如式（11）所示：

在ESS 充放电过程中，电池荷电状态随着能量的流入流出呈现动态变化。本文用ΔPESS,t表示ESS输入功率Pc,ESS,t和输出功率Pd,ESS,t之差，另外，ESS 的输入输出功率由于化学能电能转化，存在一定的损耗，本文用μESS,c表示输入的损耗系数，用μESS,d表示输出的损耗系数。因此，ESS 在充放电过程中，SOC的动态调整如下所示：

其中：PPV,ESS,t、PGrid,ESS,t分别表示t时间片PV、电网给ESS 的电能；PESS,Grid,t表示ESS 给电 网的电能。

1.3.2 PV 模型

由于PV 在未来很难采集到太阳能的准确值，EMS 通过历史数据估算的PV 数据进行调度管理。PV 首先可以为EV 供电，多余电力存储在ESS 中，或在适当时候出售给电网。它们之间的能量平衡式如式（16）所示：

其 中：PPV,t为t时间片PV 的总发电量；PPV,EV,t是t时 间片PV 给EV 的能量；PPV,ESS,t是t时间片PV 给ESS 的能量；PPV,Grid,t是t时间片PV 给电网的电量。

1.3.3 电网模型

EV 或ESS 可以直 接由电 网供电，ESS 和PV 也可以将多余的电力在适当的时间片出售给电网。因此，t时间片的电网侧能量可表示为：

其中：PGrid,b,t和Ps,Grid,t分别表示t时间片从电网购买和向电网出售的功率。

1.4 优化目标和约束条件

本文EMS 的目标是为平滑电网充电负荷，基于分时EP 满足所有EV 充电需求的同时，使PSCS 系统效益最大化，图6 为多种分布能源调度流程。由图6可知，PSCS 的效益取决于能源成本和收益。收益根据预约机制EV 信息的确定为常量，本文考虑减小成本使效益最大化。由于PV 安装后太阳能的收集成本较低，因此只考虑来自电网的电能成本。

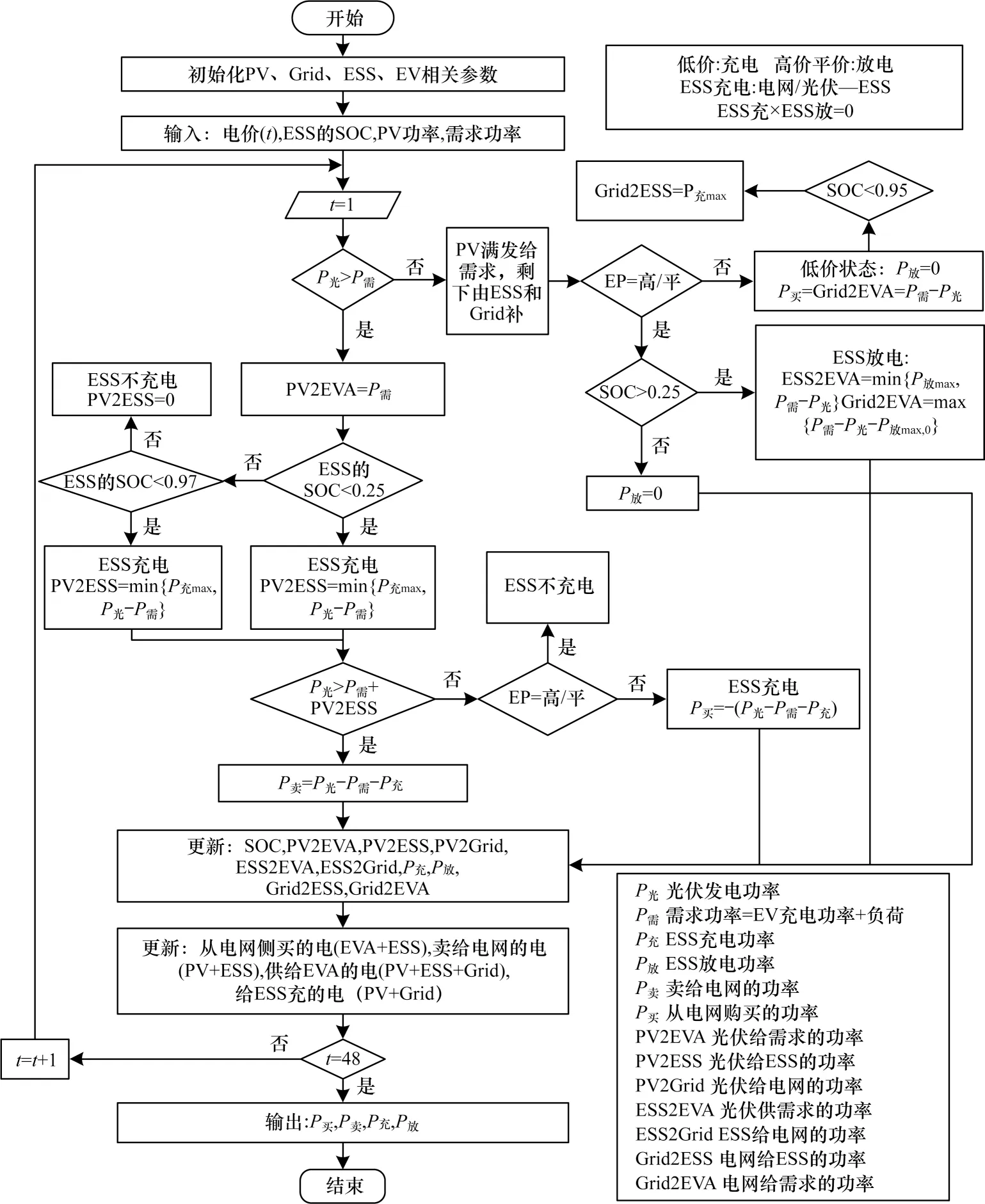
图6 多种分布能源调度流程Fig.6 Procedure of multi-distributed energy dispatch

本文寻找一个最优的智充策略，使来自电网的能量成本最小。令WI,T={wi,1,wi,2,…,wi,T,∀i}表示调度EV 所有时间片的充电决策。EV 充电的调度优化问题可表示为：

其中：fCOST表示需优化的总成本；Yb,t和Ys,t表示t时间片从电网购电和向电网售电的EP；电网、储能、充电桩可用功率的上限，分别用PGrid,max、PESS,max、Pch,max表示；QESS,max表示储能的存储容量最大限制；wi,t为决策变量；zt表示基础负荷变量。限制包括ESS 充放电约束条件、电网的功率约束、充电桩的功率约束、ESS运行荷电状态、存储容量、功率等以及ESS 充放电动作的互斥约束、负载约束。已知预测PV 发电量和基于预约机制的所有EV 的充电需求和接入时间片范围，充电调度优化问题为凸优化问题，通过现有的集中算法和策略进行求解。

2 基于EGA 的混合递推优化策略

本文基于带精英保留策略的遗传算法（Elitist Genetic Algorithm，EGA），以最小化电网成本fCOST为目标制定适应度函数，考虑EV 充电规划，通过混合递推优化策略进行能量调度。优化调度算法机制流程如图7 所示，依据传统GA 算法调整优化参数以适应模型，将改动的代码代入寻优更新即可。

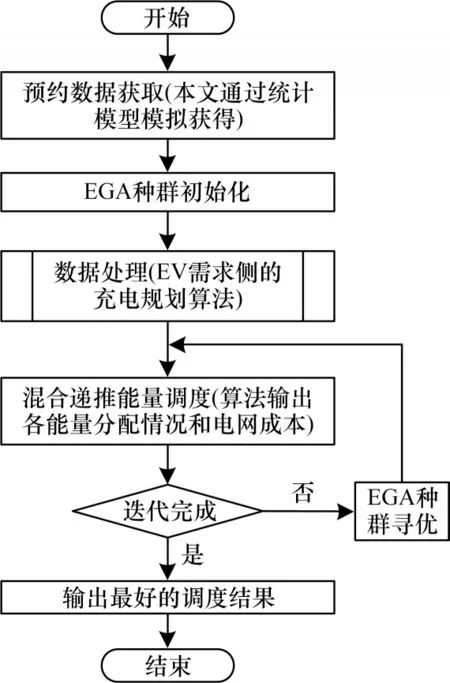
图7 优化调度算法机制流程Fig.7 Procedure of optimal scheduling algorithm mechanism

2.1 EGA 算法

EGA 算法是对原始遗传算法（Genetic Algorithm，GA）的改进，能更好地搜索全局最优解，弥补现有算法的不足，找到更好的解空间。

2.1.1 问题编码

问题编码影响了EGA 算法的可搜索性，要求EGA 算法满足3 个基本条件：完整性、非冗余、可行性。受文献［27］的启发，采用离散编码方式来构建I×T维候选解染色体，每个染色体代表问题的一个候选解，即一个调度结果。染色体在问题空间中迭代更新，得到更优的染色体。

假设染色体个体数量为C，迭代次数N，则迭代n时第c个体EVi的充电状态表示为wi,t,n,c，矩阵可以表示为Wn,c，如式（21）所示：

2.1.2 适应度函数

为了评价个体的绩效，本文使用式（22）计算每个个体的适应度值，即Ffitness。其中μ为防止适应度值为负的系数。φ和ζ是惩罚因子，当PGrid,t>PGrid,max时，φ是一个大正数。当PGrid,t≤PGrid,max时，φ=1。同理当PEV,t>PEV,max时，φ是一个大正数。当PEV,t≤PEV,max时，ζ=1。通过设置惩罚因子φ和ζ，可以在搜索过程中有效排除不符合限制条件的个体。

2.1.3 更新策略

本文采用锦标赛选择法对遗传基因进行选择。从种群中随机选择大小为k的个体群（个体被选择的概率相同），选择适应度最好的个体作为生成下一代的父体，重复操作直到新的种群规模达到原来的种群规模。通过单点交叉对选出个体进行交叉操作，发生概率为Pc，一般Pc范围设置为0.7～0.9。变异概率Pm，由于实际中变异的可能性非常小，一般将Pm范围设置为0.01～0.20。如图8 所示为变量变异示意图，通过变异来随机改变这些个体中0 和1 的数量，为不在当前种群中的个体提供一个机会，可以有效避免局部最优，扩大种群范围使算法的全局优化功能提升。

图8 变量变异示意图Fig.8 Schematic diagram of variable variation

如图9 所示为EGA 算法流程。将每代种群进化中搜索到的最优适应度值的个体best 保存为精英个体，再对剩下的个体进行遗传操作，以此避免目前种群中最好的基因受到丢失和破坏。采用EGA 拟合模型参数具有如下优点：1）保留传统GA 的可并行性，算法效率高，节省了寻优的时间；2）精英保留策略的引入，提高了传统GA 的搜索速度，全局收敛性更快。

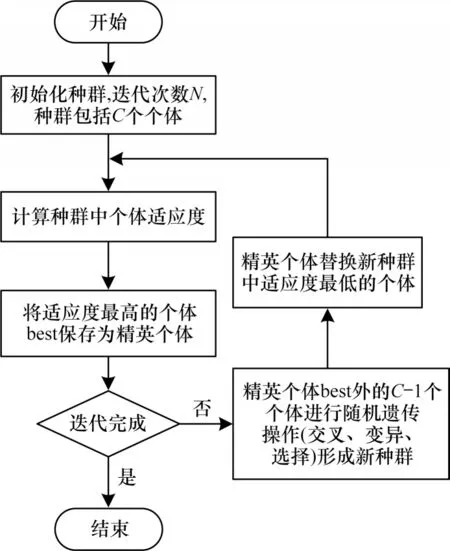
图9 EGA 算法流程Fig.9 Procedure of EGA algorithm

2.2 混合递推策略

混合递推策略即考虑充电规划的能量调度策略，包含EV 需求侧的充电规划和能量调度过程。在不同的时间片内，PSCS 的能量调度将发生变化，有以下变化情况：车辆的充电时段；ESS 的充放电数据；PV 流向数据；电网取电数据。

2.2.1 EV 需求侧的充电规划算法

本小节基于预约信息进行充电规划初步设定（充电功率的快慢和时段），具体将在在算法1 中给出。首先根据预约信息，按照EV 的需求设置充电量和停车时间，计算车辆分别采取快充和慢充两种充电方式的时间情况，生成EVs 的充电状态逻辑矩阵，为确定车辆的最佳充电方式做基础准备。

算法1EV 需求侧的充电规划算法

2.2.2 能量调度算法

能量调度算法设计采用贪婪决策方法对系统能源进行调度，考虑到最小化弃光，本文优先决策PV，基于PV 发电已知和算法1 中EV 需求侧充电规划，算法2 给出能量调度策略。首先，进行无ESS 下的充电优化，确保首先使用PV 为EV 充电。其次，找出优化区间内是否有多余PV 功率，多余功率将在合适的充电时间片向ESS 充电或在合适的销售时间片向电网出售。然后，根据EP 确定ESS 充放电周期，高EP 时期放电，低EP 时期充电。接着，基于更新后的PGrid和PESS，采用EGA 求解优化问题。最后，根据输出的最优个体更新EV 充电规划。EMS 控制每台EV 的运行并记录其工作状态。

算法2能量调度算法

3 实验结果与分析

为检测本文算法的性能，本文通过几个仿真案例进行了研究分析，选择原始遗传算法（GA）、灰狼算法（IBGWO）、粒子群算法（PSO）作为对比算法，并对相关结果进行了讨论。

3.1 参数设置

除非另有说明，模拟设置如下。本文考虑一个工作区域停车场智能光储充电站由PV 发电系统和上限PGrid,max=40 kWh/h 的电网供电。设一天为研究范围，有Δt=30 min，使T=48。

对于EV 预约数据，本文根据工作场所停车场PSCS 日常统计数据计算，发现其历史数据到达时间的分布可以近似为正态分布，其中均值和标准差分别为μA和σA，而其离开时间可以近似为一种对数正态分布，均值和标准差分别为μL和σL。车辆数量的表达式如式（23）所示：

其中：fA(t)为到达时间的概率密度函数（PDF）；FA(t)为相应的累积分布函数（CDF）；MA,t为t现存的车辆数，MA,t∊(0，I)。根据对 数正态 分布函 数μD和σD两个参数，可以近似得到EV 行驶距离的累积分布函数，其表达式如下：

其中：μD、σD分别为函数的期望值和标准差。每辆即将到来的电动汽车的预约充电需求可由给出。

调查数据显示，早晨08∶00 左右为上班用车期，晚上18∶00 左右为下班用车期，在此EV 的到达时间和离开时间分布参数依次为（μA=7∶30，σA=3）和（μL=17∶30，σL=3），如图10 EV 的SOC 分布图所示。假设EV 的规格相同，本文采用蔚来汽车ES6/ES8/EC6 等常用EV 容量，电池容量设置为70 kWh。EV 初始SOC值均匀地从区间[0，1]随机设置，目标SOC设为1。基本负荷信息以负荷预测的结果为基础，EV 预约充电信息如表1 所示。具体的系统参数如表2 所示，分时电价如表3 所示。假设出售给电网的电价是购买电价的1/5。

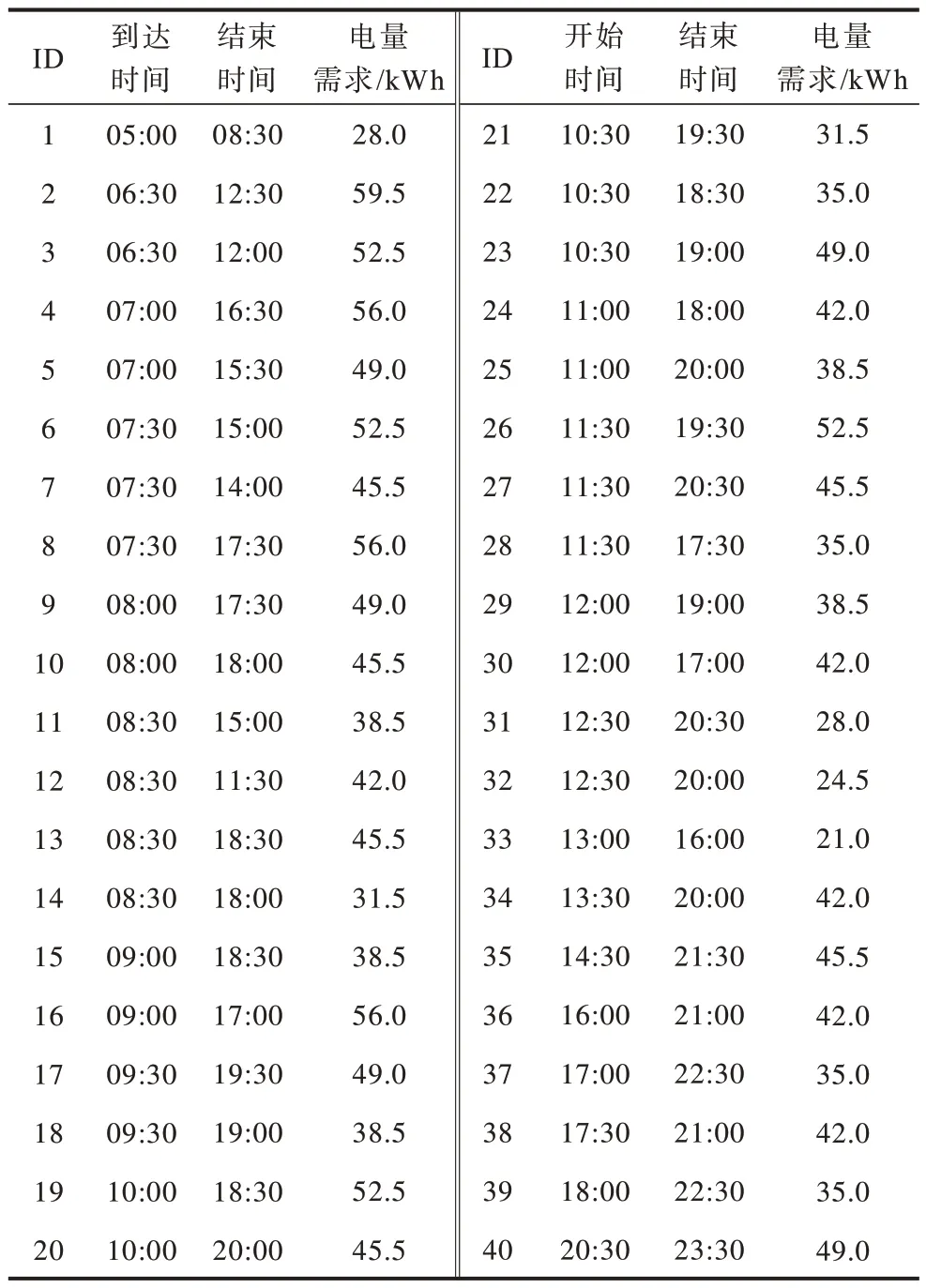
表1 EV 预约充电信息Table 1 EV booking charging information

表2 系统参数Table 2 System parameters

表3 分时电价Table 3 TOU power price 单位：（元·kWh-1）

图10 EV 数量的SOC 分布图Fig.10 SOC distribution map of EV number

本文的PV 发电数据由宁德时代示范点［28］提供。试验仿真平台使用Python 语言搭建，运行于Intel Core i5（2.3 GHz）处理器和8 GB 内存的计算机中。

根据前文设置的参数，本文设定几个测试案例：

1）没有ESS 和PV 的EV 充电站：生成此案例场景是为了获取在没有ESS 和PV 的情况下EV 充电站的运行成本。EV 的总充电功率来自电网。仅接电网的停车场，EV 从到达时开始充电，充电过程不间断。需要注意的是，满足EV 充电需求的电网供电没有限制。本案例的表现是评价其他研究案例的基础。后增加算法和策略进行优化，得到停车场的运行状态和用电成本。

2）有ESS 没有PV 的EV 充电站：本测试案例目的是评估在EV 充电站部署ESS 的算法，测试ESS 在EV 充电站发挥作用的情况。当附近没有可用的可再生资源时，ESS 可调控不同电价时刻的购电情况，从而为EV 充电站运营商提供购电差利润。

3）基于ESS 和PV 的EV 充电站：本测试案例是为了评估本文算法在基于PV 的EV 充电站中部署ESS 的有效性。

4）考虑到充电汽车数量大幅减少的情况，本文采用此案例测试基础运营情况下的调度。对其整体运行负荷进行评估。

前3 种情况下充电站最终需求充电负荷分布如图11 所示。可以看出，3 种情况下充电站的EV 充电负荷分布趋势明显不同。在所有情况下，案例3 的高峰时间片的充电需求明显向其他时间片进行转移。这是因为PV 和ESS 的联合优化使需求的可转移空间变大，从而有利于案例2 向低峰时间片转移，而案例1 的可转移灵活性较差。

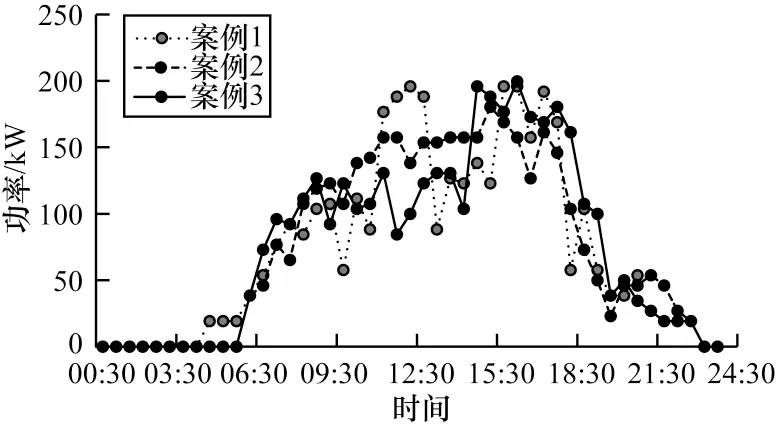
图11 EV 需求充电负荷分布Fig.11 Distribution of EV demand charging load

3.2 实验结果与分析

3.2.1 不同测试案例下的能量管理情况

本文通过研究不同测试案例下的能量调度情况来验证本文针对PSCS 系统的设置的能量管理策略。图12 所示为不同案例下电网供电及能源动态情况，其中图12（a）和图12（b）表示表示案例1 使用算法和策略前后的EV 充电功率，可以看出EV 从到达时间开始充电，峰值负荷将大幅上升，对电力系统的安全运行产生一定的威胁，且面临高峰用电罚款，这显然不是停车场经营者想要的。停车场经营者在建造初期就会设定好每个车位都开始充电时的最高额定功率，所以应允许所有车开始充电。为实现削峰填谷，控制峰值负荷，本文设计需求策略和算法来完成EV充电的简单调度。通过EV 充电功率曲线对比，算法和需求策略可以在不超过电网功率限制的情况下有效地将EV 负载转移到低EP 时间片。由于停车场内只有电网提供电力，在这种情况下，EV 充电负荷等于电网的电力。

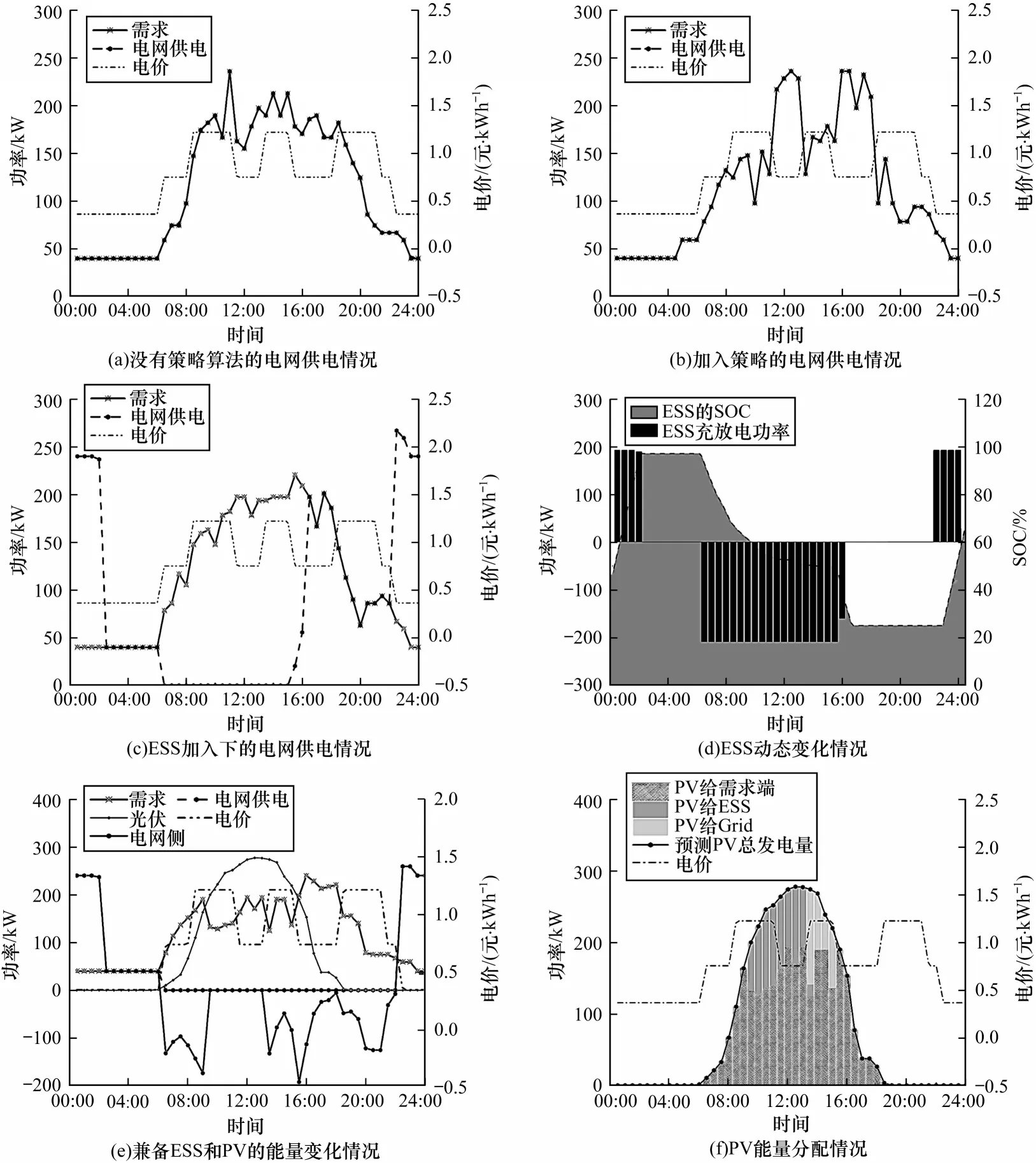
图12 不同案例下电网供电及能源动态情况Fig.12 Grid power supply and energy dynamics in different cases

如图12（c）和图12（d）分别展示了ESS 加入下的电网供电趋势和ESS 的动态变化情况，可以看到由于ESS 的加入，来自电网的功率在高EP 期间大幅降低，很好地将电网的大部分负载需求转移到ESS。ESS 在高EP 期间释放存储的能量给EV 充电，与图图12（a）和图12（b）相比，充分利用低EP 期间以最大电网功率限制对ESS 进行充电，并为下一个高EP 时间储存能量，获得最大的经济效益。在高EP 周期结束时，ESS 将放电到最小容量限制。因此，在这种情况下，ESS 被充分利用来为EV 充电，其总输出功率受其最大容量的限制。

图12（e）和图12（f）表示兼备ESS 和PV 的能源动态趋势和PV 能量分配情况，在PV 和ESS 的配合下，用电需求在低EP 时期更加集中。由于PV 的作用，在高EP 期间，只从电网购买少量或不购买电网电力。PV 和ESS 在降低电网功率方面起着重要作用。减少ESS 的充放电次数有利于延长ESS 的使用寿命。当未来优化范围内充电负荷较低时，可以明显看出，从09∶00 到16∶00，优化范围内的PV 功率远大于EV 负载。多余的PV 电能存储在ESS 中，用于为即将到来的EV 充电或根据EP 出售给电网，当ESS 储能达到最大容量限制时，则直接出售给电网。同时，在保证ESS 存储足够电量且满足未来到达EV充电需求的前提下，EMS 可选择在高EP 时间片将多余的PV 电力出售给电网，如图12 中13∶00 到16∶00所示。如果总是优先给ESS 充电，很有可能在ESS达到容量限制后，在低EP 期内会有多余的PV 电量，不得不低价卖给电网。与此相比，本文提出的策略具有更好的经济效益。

图13 所示为能量管理后的各能源变化示意图，其中图13（a）表示总的需求功率供电分配情况，在00∶00 到06∶00 低EP 期间，由于PV 还未开始发 电，EMS 设定减少ESS 充放电次数，需求在此阶段由电网直接供电。在06∶00 到22∶00 中 高EP 期 间，由ESS 和PV 协作供电，充分发挥两者的调度作用，从而减少充电站投资电力成本。图13（b）表示ESS 的动态变化情况，展示了基于ESS 和PV 的EV 充电站在分时电价下ESS 的充放电情况以及内部能源动态变化情况，在低EP 时期，ESS 的SOC 上升的主要供给方为电网，在09∶00 到14∶00 期间，若PV 在保证EV 充电后仍有大量剩余则供给ESS 充电。EV 充电站的充放电口功率大小根据ESS 的SOE 和PV 的预测发电量来计算。当有ESS 无PV 的时候，可以采取低价买电高价卖电，但是这样会加大ESS 的充放电频率，造成ESS 使用期限内的提前衰化，所以需要评估ESS 寿命电池损耗的代价和挣中间差价的利润大小，进行代价和利润的权衡。

图13 能量管理后的各能源变化示意图Fig.13 Schematic diagram of the change of each energy source after energy management

从这几个案例中可以看出，ESS 和PV 系统对于降低整体充电成本至关重要。

表4 为本文4 个不同案例设置详情的比较，其中：YES 表示有此项；NO 表示没有此项；YB 表示有较大容量的此项；Y200 表示容量为200 kWh 时的调度。在案例1 中，采取EGA 算法和需求策略使成本降低了6.3%。虽然在没有ESS 的情况下节省的费用很少，但该策略有效降低了系统的运行成本。与案例1 相比，案例2 增加了ESS 的部署，使其降低了55.0%的成本。与案例2 相比，案例3 在有ESS 的情况下增加了PV 的使用，成本在原先基础上又降低了81.5%。当PV 和ESS 加入到系统中时，大幅降低了运行成本。与案例1 相比，案例2 和案例3 的成本分别降低了55.0%和91.7%。

表4 不同案例的设置详情Table 4 Setting details of different cases 单位：元

在案例3 中，YB 指有大规模部署，结果表明，同比增大ESS 的储电量，反而增大了50.2%的成本，由此看来，ESS 的部署不可盲目增大，需要与系统对应设施相匹配。同比增大PV 的发电量，则成本为负，因为PV 发电充裕，在满足EV 负荷的前提下，将多余的电力卖给电网盈利。

本文基于现实场景下构建模型，更好拟合实际场景下的电力动态情况，在精细化程度和逻辑可靠性上优于简单框架［17］，更符合当前环境下PSCS 的应用环境。

3.2.2 与其他算法的比较

为更好证明本文算法的有效性，将本文算法与GA、PSO、IBGWO 算法进行了比较，结果如表5 所示，其中算法平均成本表示两个算法处理后的平均成本。

表5 不同算法的结果对比Table 5 Comparison of results of different algorithms 单位：元

由表5 可以看出，随着个体数的增大，EGA 和GA 寻优效果分别提升了7.1%和5.1%，将迭代次数增加，则分别提升了3.7%和4.8%。对比平均成本和最优成本可以看出，EGA 算法比GA 算法和IBGWO算法的性能更好。与GA 算法相比，EGA 算法的平均成本和最佳成本分别降低了2.2% 和2.1%。与IBGWO 算法相比，本文算法则分别降低了15.4%和14.2%；与PSO 算法相比，EGA 算法的平均成本和最佳成本分别降低了20.3%和21.9%。

由表5 还可知，EGA 算法和GA 算法在成本优化的实验结果上比IBGWO 算法和PSO 算法优越20.0%。从算法特性分析，EGA 算法、GA 算法等遗传算法对连续性和离散型数据模型均友好，算法复杂度不会产生较大波动，IBGWO 算法和PSO 算法模拟自然界群体收敛目标行为，收敛行为多用于衡量连续性动作和变化，且有较好的结果，算法复杂度不会有量级变化。本文面向符合离散数据模型的场景，匹配解决离散数据模型的分析算法，适应度会较高，能够取得较好的成果。

图14 所示是不同算法的性能对比，可以发现，随着个体数和迭代次数的调整，算法性能有明显的优化，但由于受到时间复杂度的制约，参数继续上调算法的寻优效果不明显。如图14 中IBGWO 灰狼算法和PSO 粒子群算法相比，由于IBGWO 灰狼算法更适用于此算法参数狼数较少的（10～50），而粒子群算法的参数粒子数相对较多的（100-20/50），实用性的差别导致在选用统一参数平相对比时，两者的结果与理论所阐述的效果符合程度不高，总体效果没有遗传算法在本文所建模型的表现效果好。因此，实验证明，本文算法和提出的改进策略可以很好地提高求解的稳定性和效率，大幅提高了在解决实时调度问题中的实用性。

4 结束语

本文基于RGAHR 算法，提出一种面向汽车充电预约的PSCS 系统上下层优化的调度策略，目的为优化调度主次，使EMS 在电网侧取电时的成本消耗最小。实验结果表明，在调整参数的模型下，基于RGAHR 算法的调度策略依旧有效，并随着迭代次数的增加，优化效果更加明显。另外，加入贪心依序递推机制可有效在光伏和EV 负荷不确定的情况下合理规划充电及供电来源和时段，显著降低光储充电站运行的电网取电成本。因此，本文方法可以为多种不同的EV 充电模型和差异化电价趋势模型提供参考，能为PSCS 合理配备ESS 和PV 提供科学经济的部署方案。下一步将在模型构建方面进一步考虑EV 双向充放电情况下，光储充电站经济部署PV 和ESS 所需的补贴金额，以达到系统内部能源配置调度运行成本最小的目的。在优化算法方面，本文将基于多种目标寻优扩大调度的全面性，针对部署和运营两部分进行成本最小化调度分析。