2023年新疆高三第一次适应性检测一道几何试题的探究

张元志

⦿ 新疆昌吉州第一中学

1 题目

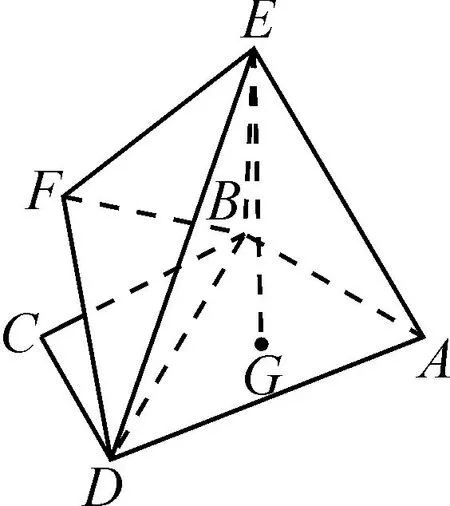
图1

(1)求证:EF⊥BD;

(2)若点G为△ABD的重心(三条中线的交点),EG⊥平面ABD,求直线BD与平面ABE所成角的余弦值.

2 解法分析及详解

2.1 第(1)问思路及解析

第(1)问思路及解析如下.

思路1：利用直线与平面垂直的判定定理,证明异面直线垂直问题.

思路2：利用向量坐标运算证明异面直线垂直.

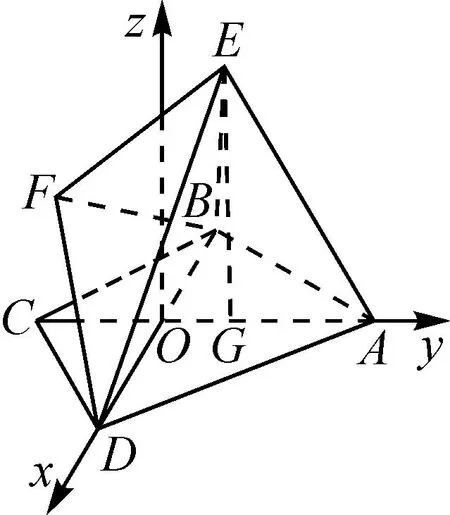
图2

2.2 第(2)问思路及解析

建立空间直角坐标系,确定相关点的坐标,可用三种方法计算平面ABE的法向量.依据该思路,绘制如图3所示的思维导图.

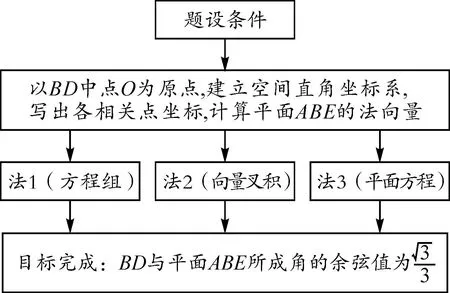
图3

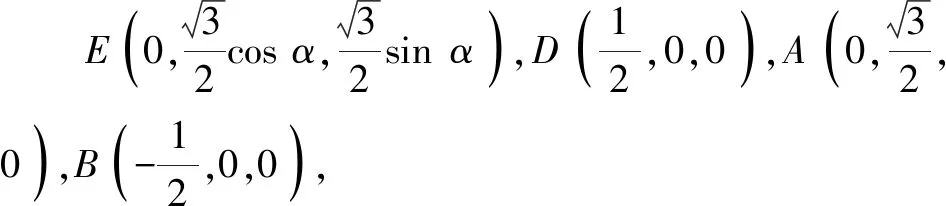
下面计算平面ABE的法向量,有如下三种方法.

3 相关链接

链接1(2020年天一大联考高三皖豫联盟体第三次考试·理)如图4,在正方形ABCP中,AB=4,D是CP的中点.把△ADP沿AD折叠,使△PAB为等边三角形,得到如图5所示的几何体.

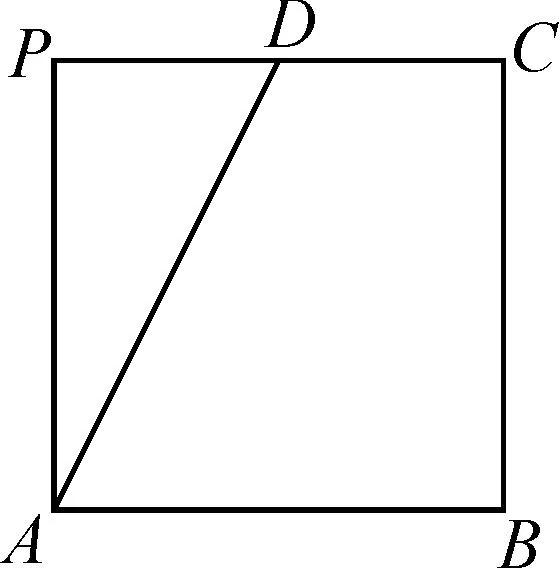
图4

图5

(Ⅰ)证明:AB⊥PD;

(Ⅱ)求二面角A-PB-C的余弦值.

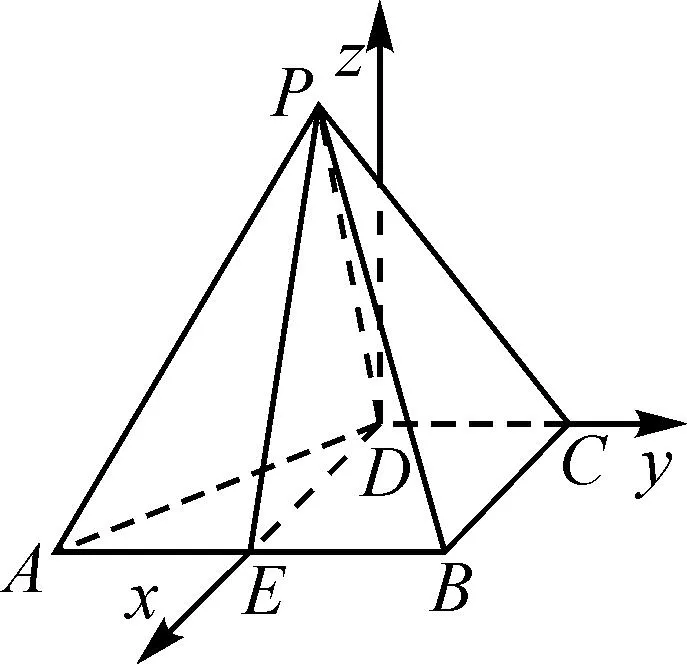
图6

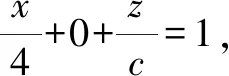
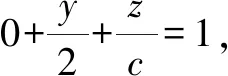
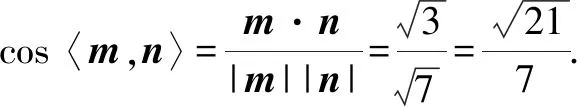
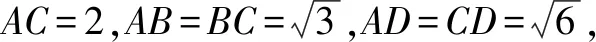
图7

图8

(1)求证:BD⊥AC;

(2)求二面角A-BD-C的余弦值.

(1)证明：略.

图9

同理,平面CBD的一个法向量为n=(-3,1,2).

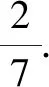
向量坐标法,程序化强,易于操作.解题成功的关键,是平面法向量的计算:方程组法是通法,向量叉积属于高等运算,平面方程法是思维的拓展.Z