对一道圆锥曲线问题的探究与拓广

郭永生

⦿ 山东省菏泽市定陶区第一中学

一套成功的试卷总是不乏好题,立意新颖,典型突出,亮点十足,引人注目.这类试题往往知识融合自然,考点科学交汇,具有良好的教研价值,倍受众多数学爱好者青睐,非常值得我们深入思考、分析与探究.

1 问题呈现

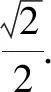
(1)求轨迹E的方程.

(2)设过点A(0,-1)且斜率为k1的动直线与轨迹E交于C,D两点,且点B(0,2),直线BC,BD分别交圆x2+(y-1)2=1于异于点B的点P,Q,设直线PQ的斜率为k2,问是否存在实数λ,使得k2=λk1成立?若存在,求出λ的值;若不存在,请说明理由.

2 问题解答

上述问题的解答如下.

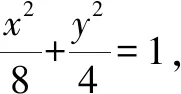
(2)由题意知,直线CD的方程为y=k1x-1.设C(x1,k1x1-1),D(x2,k1x2-1).

将y=k1x-1与x2+2y2-8=0联立,消去y,得

设直线PQ的方程为y=k2x+m,P(x3,k2x3+m),Q(x4,k2x4+m).

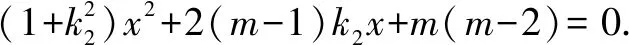
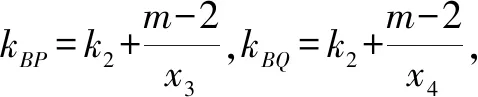
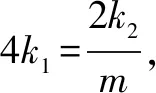
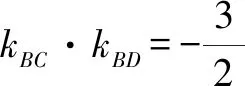
3 问题探究

经过初步探究,发现:

设M(dy1+t,y1),N(dy2+t,y2),则

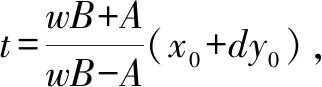
特别地,可得以下结论:

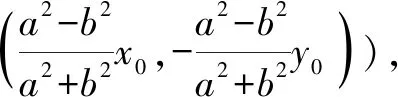
当TM⊥TN时,则直线AB恒过点(0,0).

(注:上述e为相应曲线的离心率.)

4 拓广探索

再进一步深入研究抛物线,发现类似性质:

特别地:

(1)当TM⊥TN时,时,直线MN恒过定点(2p+x0,-y0);

(2)当x0=y0=0,且TM⊥TN时,直线MN恒过定点(2p,0).

5 链接高考

(1)求C的方程;

(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.

图1

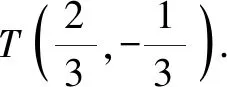
当下高中数学教学面临新教材、新课程、新高考所引领的三新环境,单纯从学科教与学的角度来看,学习探究应该成为适应新时代下教与学的新常态,特别是像学习圆锥曲线等一类难度较大的内容时,教师更有必要下功夫思考与探究.圆锥曲线的性质十分丰富,可供探究的方面十分广泛,以上笔者所探讨的这些只不过是圆锥曲线性质中的冰山一角,沧海一粟,期盼早日见到新时代同行们更多、更好的教学研究成果,以期同学习、共进步!Z