基于梁格法的非对称斜拉桥施工阶段索力分析

吴文杰，杨 凯

(1.甘肃铁科建设工程咨询有限公司,甘肃 兰州 730000; 2.陕西铁路工程职业技术学院,陕西 渭南 714000)

0 引言

近年来,随着我国交通事业的发展,各级公路的建设日趋完善,与此同时,斜拉桥的建设也得到了空前的发展。学者们针对非对称斜拉桥的力学性能进行了部分研究。但由于此类斜拉桥为高次超静定结构,受力复杂,施工阶段索力监测控制难度极大[1]。为此,本文以某非对称梁斜拉桥为例,基于梁格法研究非对称斜拉桥的施工阶段索力变化情况,为后续此类斜拉桥的施工索力控制提供借鉴。

1 工程概况

某独塔双索面混合梁斜拉桥主桥长243 m,宽44 m。其主跨为158 m钢箱梁,辅跨45+40=85 m为混凝箱梁,其中,钢梁与混凝土梁之间通过钢-混结合段连接;斜拉桥桥塔高度为107 m,斜拉索采用双索面扇形布置[2]。桥梁立面布置如图1所示。

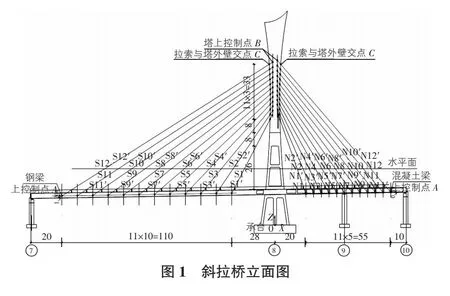
2 有限元模型的建立

斜拉桥主梁为混合梁结构,钢箱梁和混凝土箱梁皆为单箱九室,依据纵向梁格的划分原则,将梁截面划分为10片纵梁梁格,钢箱梁部分梁格间距为3.3 m,混凝土箱梁梁格间距为5 m。梁格划分如图2,图3所示。

采用Midas Civil 2022有限元软件建立全桥空间模型,桥塔和主梁采用梁单元,梁单元共2 565个,斜拉索采用桁架单元,桁架单元48个;混凝土梁(塔)和钢梁(塔)以共节点的方式与刚混段连接。主墩的模拟类似于混凝土塔[2]。建立的空间有限元模型如图4所示。

3 施工阶段索力分析

3.1 施工阶段的划分

根据非对称斜拉桥的结构特点,结合设计规范,本文斜拉桥的施工阶段划分如表1所示。

表1 桥梁施工阶段划分

3.2 施工索力计算分析

本桥拉索张拉分两次张拉。第一次张拉控制目标值为成桥索力的50%[3],二次张拉后要求达到除二期以外的索力[4]。

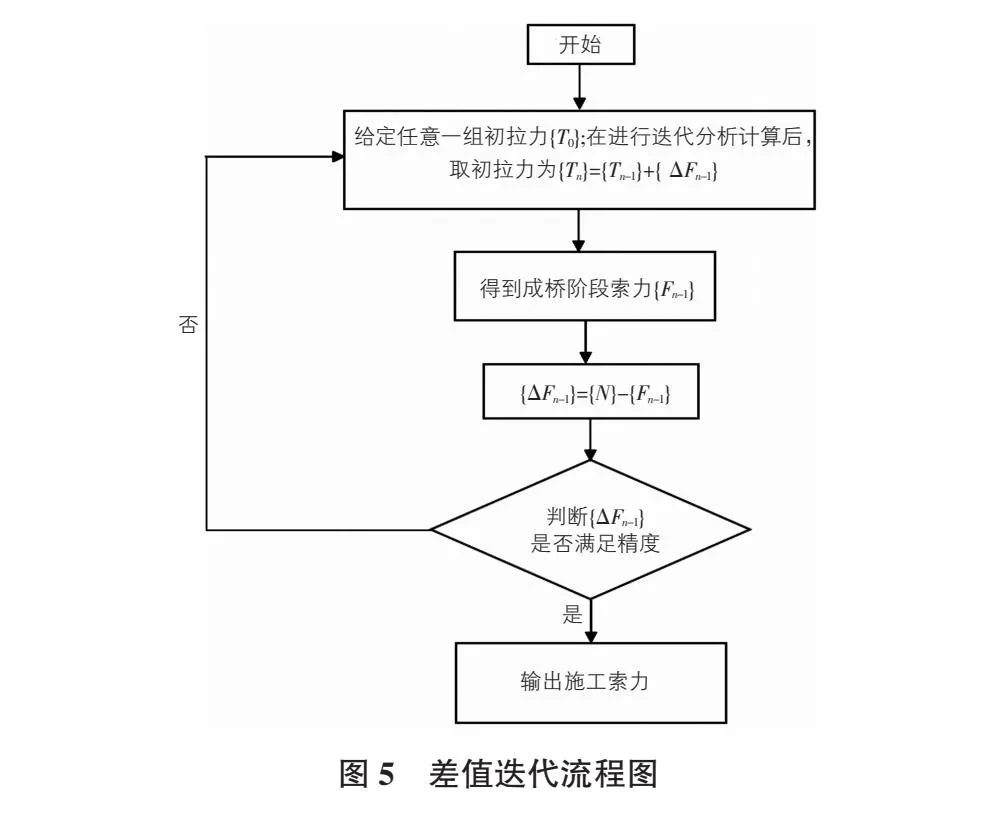
采用Midas Civil 2022有限元软件中的差值迭代法来计算施工索力[5-6]。用差值法进行正装迭代计算施工索力时,其流程图见图5。第二次施工索力迭代计算表见表2。

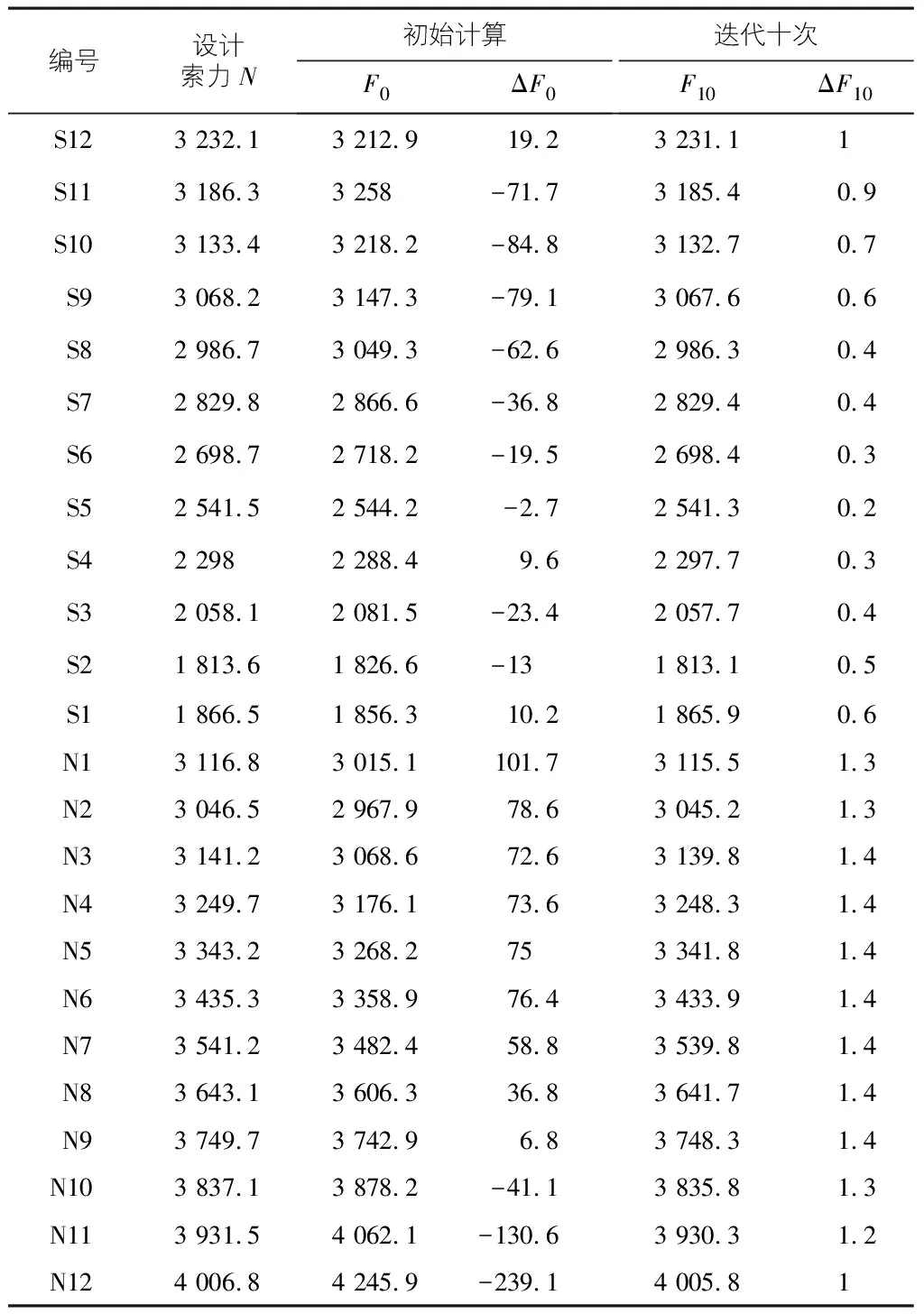
表2 第二次施工索力迭代计算表 kN

由表2可知,与设计索力值相比,初始计算得到的成桥索力误差较大,最小误差值为N9号索,其值为6.8 kN;误差最大的为N12号索,其值为-239.1 kN,其他各斜拉索索力值介于二者之间,其原因主要是在有限元计算时,初始索力值设置不同,其迭代结果所受影响也较大。随着迭代次数的增加,其收敛速度放缓,计算耗时增加,经过3次迭代后其误差值出现减小趋势,经过10次迭代计算后,有限元所得成桥索力值与设计成桥索力值基本一致,最小误差值为S5号索,其值为0.2 kN;误差最大的为1.4 kN,根据设计及相关规范要求,其迭代后索力可满足施工精度要求。

一次张拉完成后和二次张拉后铺装前以及铺装前后左侧斜拉索索力对比如图6—图8所示。

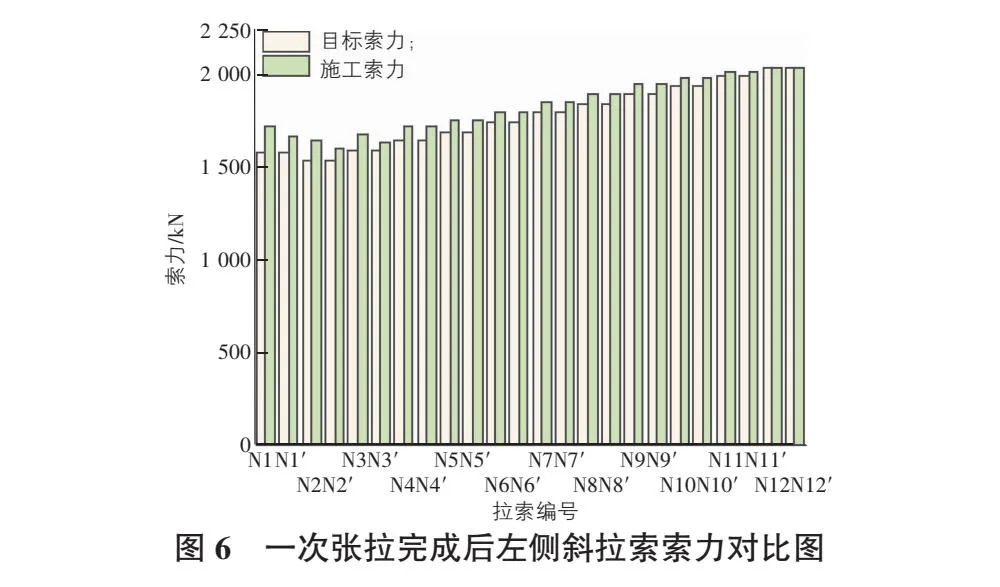
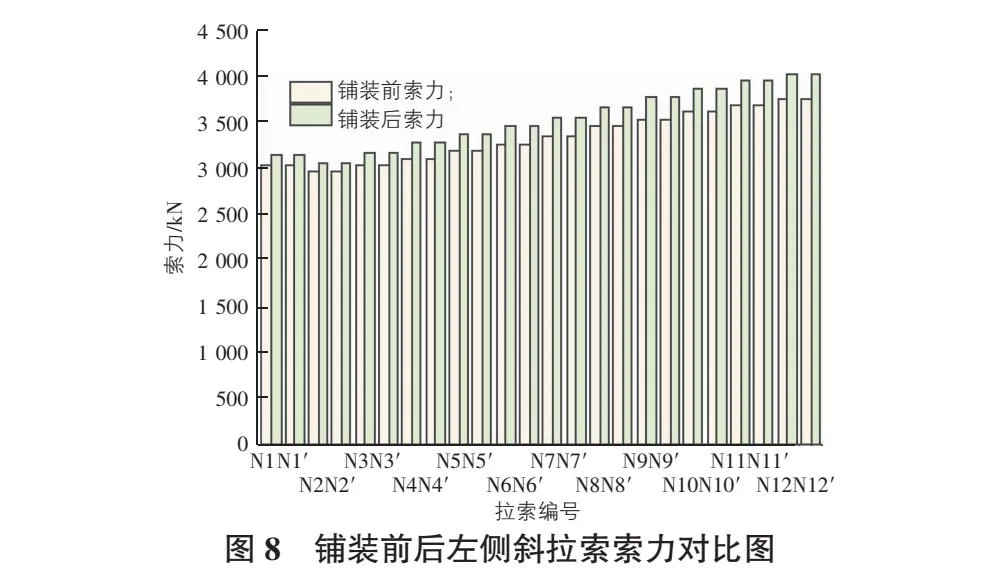
由图6—图8可以看出,第一次张拉结束后,最后张拉的两对索的索力与目标索力接近,而其他斜拉索索力比目标索力小,其原因主要是斜拉索与桥塔和主梁组成的是一个超静定结构体系,拉索索力之间存在耦合关系,其中一条拉索索力变化会引起其他索力的变化,且距离变化索力越近的斜拉索所受影响越大。二张后斜拉索索力变化情况与一张趋势相同,与铺装前相比,二期铺装完成以后斜拉索索力明显增大,原因是桥面铺装导致主梁上部荷载增加,所以索力增大。

3.3 施工方法对拉索索力的影响分析

为研究施工方法对斜拉索索力的影响,对比两种施工方法,第一种是主塔、主梁施工完成后再挂索张拉,且同一批次的斜拉索采用对称张拉;第二种是主塔施工完成后,对角和对称张拉相结合的方式进行施工。计算结果见表3,表4。

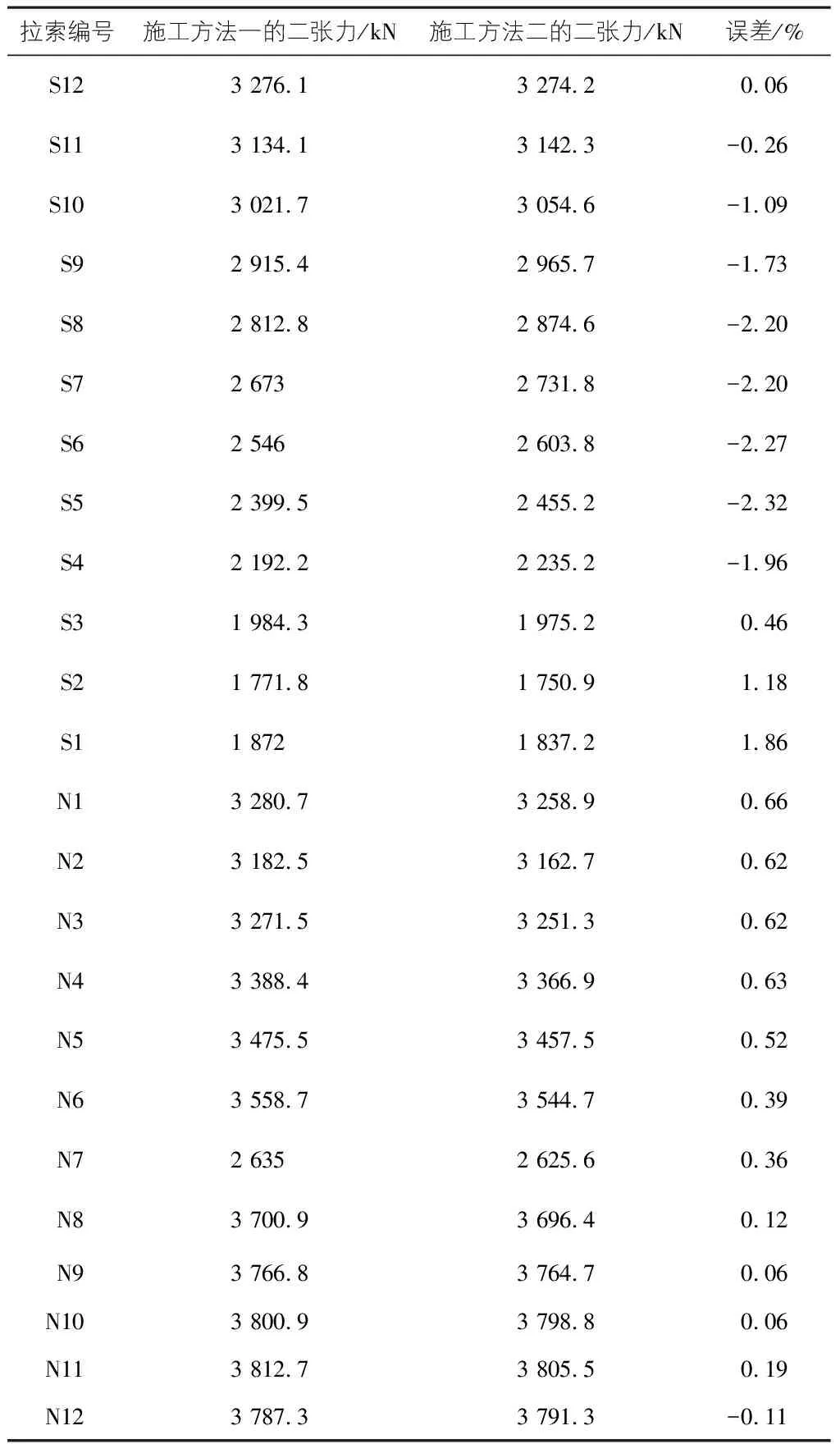
表3 不同施工方法右侧拉索二张力对比

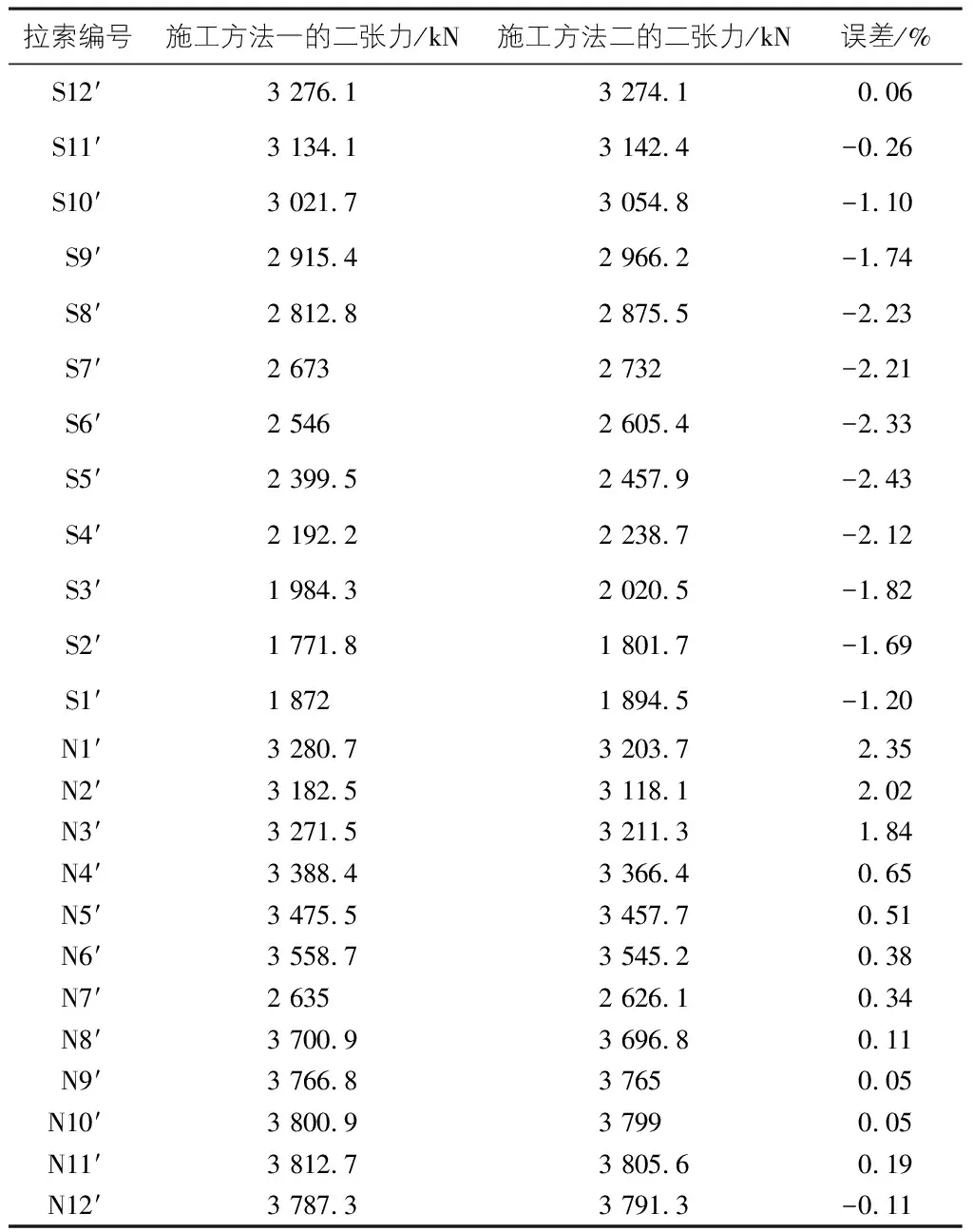
表4 不同施工方法左侧拉索二张力对比

由表3和表4可以看出,施工方法对斜拉索的二张施工索力会有影响,但两种不同施工方法下,斜拉桥左右两侧斜拉索索力值误差不超过3%,其原因主要是在主梁施工完成时,斜拉索的不对称张拉会引起索力值的改变,但这种影响相对较小;说明在满足施工质量的前提下,可适当调整非对称斜拉桥的施工拉索方式,以满足现场和施工进度要求。同时,钢梁斜拉索索力值的误差要比混凝梁大,说明该类斜拉桥的钢梁内力变化对拉索索力的变化更为敏感。

4 结论

通过基于梁格法的非对称斜拉桥施工阶段索力分析得到以下结论:

1)采用差值法计算得到的成桥索力经过10次迭代后可满足施工要求。2)斜拉索与桥塔和主梁组成的是一个超静定结构体系,拉索索力之间存在耦合关系,距离变化索力越近的斜拉索所受影响越大。二期铺装完成以后斜拉索索力增大明显。3)在满足施工质量的前提下,可适当调整非对称斜拉桥的施工拉索方式,以满足现场和施工进度要求。同时,该类斜拉桥的钢梁内力变化对拉索索力的变化更为敏感。