复杂载荷作用下梁弯曲的重心插值配点法★

赵晓伟，王守波，李广惠

(1.山东建筑大学,山东 济南 250101; 2.山东省建设建工(集团)有限责任公司第四分公司,山东 济南 250014)

0 引言

材料力学中采用弯矩方程积分法求平面弯曲梁的挠度和转角问题。首先建立梁的挠曲线近似微分方程, 进行两次积分运算再根据边界条件确定积分常数,从而求得挠度方程和转角方程。但是这种方法分析梁的弯曲变形时,需先确定梁的弯矩方程,当梁上作用复杂载荷时,确定梁的弯矩方程变得十分困难[1-3]。载荷方程积分法[4]需要进行四次积分运算结合边界条件才能得到挠度方程。当梁上作用复杂载荷时,载荷方程积分法运算过程烦琐冗长。这两种方法在工程实际计算中受到很大的限制。

在实际工程应用中,求解平面弯曲梁挠度和转角问题可以看作是微分方程边值问题。目前求解常微分方程的边值问题的方法主要有有限元法和有限差分法[5],这两种方法的计算精度取决于对求解区域划分单元的大小。而配点法求解此问题不需要划分单元,不需要积分,公式也简单,容易编程。配点法主要有拟谱法和微分求积法两种。拟谱法[6]将未知函数展开为谱函数的线性组合,这种方法的理论研究还在进一步的发展,在工程技术人员中应用不广泛。微分求积法[7-8]是将未知函数在区间上所有离散点的函数值的加权和来逼近该函数在某一离散点的偏导数或积分,其权系数的确定通常根据Lagrange多项式在网格点处的导数值给出。因此,离散点不能取得太多,否则Lagrange多项式表示的曲线随多项式次数的升高而出现Runge现象,从而产生计算的不稳定性[9-11]。而重心Lagrange插值[12]很好地避免了这些缺点。

采用重心插值配点法就是用重心Lagrange插值多项式求出某一函数在各个离散点的微分矩阵,从而可以通过矩阵的运算来求出常微分方程的解。而材料力学中梁弯曲问题的求解最终也归结为在一定的边界条件和初始条件下的(偏)微分方程(组)的求解,所以,可以把重心插值配点法作为用于材料力学问题的求解的一种数值方法。本文把重心插值配点法用于平面弯曲梁的挠度问题的分析中,计算结果精度较高,效果满意。

1 微分矩阵

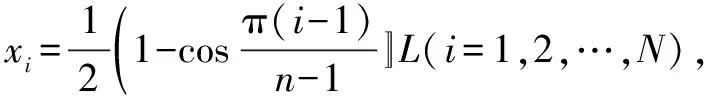
(1)

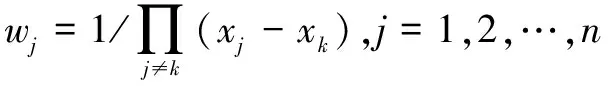
对g(x)求n阶导数,得式(2):

(2)

函数g(x)在节点x1,x2,…,xN处的n阶导数表示为式(3):

(3)

式(3)可写成矩阵形式(见式(4)):

g(n)=D(n)g

(4)

对式(2)求导直接得到一阶微分矩阵,通过下面递推公式得到高阶微分矩阵(见式(5)—式(7)):

(5)

令:

(6)

w(n)=DNg

(7)

于是,对微分方程的求解就变成对线性方程组的求解,就线性方程组(7)可以得到未知函数的离散值。

2 复杂载荷梁弯曲问题

2.1 梁控制方程

细长梁(见图1),承受集度为q(x)的荷载,发生弹性弯曲,控制方程为:

EIw(4)=q(x)

(8)

其中,E为截面弹性模量;I为截面惯性矩;w为梁的挠度;q(x)为梁的荷载集度。

梁的挠度,记为w=w(x),转角即为梁横截面对其原来位置转过的角度,记为θ=w′(x)。

图1所示简支梁的边界条件如式(9)所示:

w(0)=0,w(L)=0,w″(0)=0,w″(L)=0

(9)

因此,图1任意载荷下的梁的弯曲变形问题,就是在边界条件式(9)下,求解微分方程式(8)边值问题。

2.2 梁弯曲控制方程的重心插值配点法公式

在梁上取N个节点,则w(4)可用微分矩阵对N个节点值w求导表示,写成矩阵形式见式(10):

(10)

D4w=f

(11)

由式(11)即可求得梁的节点位移列阵。微分矩阵以及梁节点位移的计算,本文都编制Matlab程序来实现。

3 数值算例

算例1:图2所示简支梁AB,梁长50 cm,高2 cm,宽1 cm,弹性模量为10 GPa,q0=100 N/m,得到梁轴线各节点的挠度和转角,与解析解比较如表1所示(选取13个节点计算)。

表1 算例1梁各节点挠度、转角的解析解与本文解比较

由表1,图3,图4可知,承受正弦荷载作用的简支梁,划取13个节点,用重心插值配点法计算出的挠度和转角结果与文献[4]精确解完全吻合,挠度和转角最大相对误差为10-9,充分说明了重心插值配点法计算复杂载荷受弯梁挠度和转角的可行性和精确性。

算例2:一悬臂梁承受荷载如图5所示,其他参数同算例1,得到梁轴线的各节点挠度、转角,与解析解比较如表2所示(选取12个节点计算)。

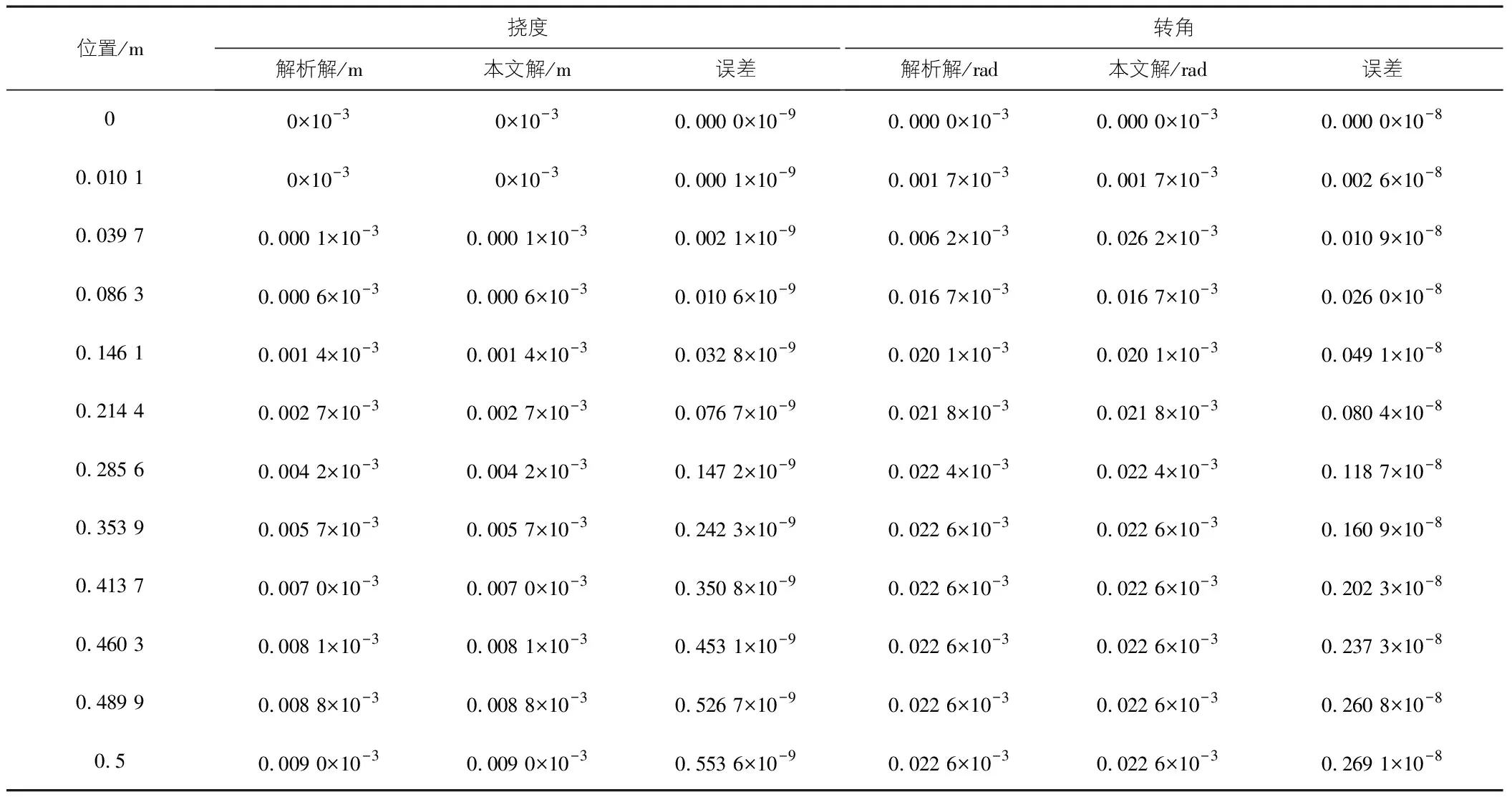
表2 算例2梁各节点挠度、转角的解析解与本文解比较

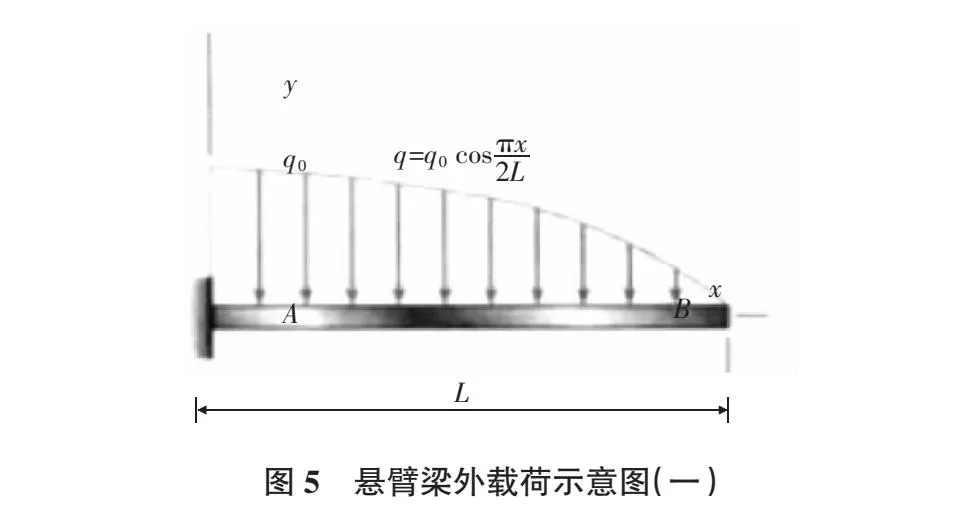
由表2,图6,图7可知,承受余弦荷载作用的悬臂梁,划取12个节点,用重心插值配点法计算出的挠度和转角结果与文献[4]精确解完全吻合,挠度和转角最大相对误差为10-9～10-8,充分说明了重心插值配点法计算复杂载荷受弯梁挠度和转角的可行性和精确性。

算例3:一悬臂梁承受荷载如图8所示,其他参数同算例1,得到梁轴线的各节点挠度、转角与解析解比较如表3所示(选取7 个节点计算)。

表3 算例3梁各节点挠度、转角的解析解与本文解比较

由表3,图9,图10可知,承受抛物线荷载作用的简支梁,划取7个节点,用重心插值配点法计算出的挠度和转角结果与文献[4]精确解完全吻合,挠度和转角最大相对误差为×10-14,充分说明了重心插值配点法计算复杂载荷受弯梁挠度和转角的可行性和精确性。

4 结论

1)本文方法利用微分矩阵来求解,可得到非常精确的挠度和转角,非常适用于求解承受复杂载荷的细长梁,更便于求解承受非线性分布荷载弯曲梁。从算例中可以看出,数值解与精确解完美吻合,验证了重心插值配点法在梁的弯曲变形计算中的可行性和精确性[14]。该方法不仅有较高的精度,还具有极好的数值稳定性。2)该方法可用于材料力学弯曲变形课堂教学,可让学生借助Matlab语言编程计算获得数值解,并与精确解进行对比,可让学生体会到求解问题的多样性,提高学生的学习兴趣和热情。3)这种方法便于处理边界支承条件,可以用叠加法也可以用替代法,编制程序时非常容易实现边界条件的施加。且数学原理简单,容易编制程序,因此在结构分析中,有良好的应用前景。