SSA-SARIMA 组合模型的桥梁健康状态预测

谌桢文，常 军

（苏州科技大学 土木工程学院，江苏 苏州 215011）

桥梁健康监测系统用于实时掌握桥梁的健康状况。通过安装不同类型的传感器可以掌握桥梁的整体信息，并通过适当的处理，可用于传统的损伤识别和结构状况评估[1-2]。其中，如何建立一个具有高精度的预测模型，准确地对监测数据进行预测是结构状态评估的关键，对于桥梁安全预警及后续管养工作具有重要意义。这些数据往往是含有等时间间隔的数据。因此，时间序列分析理论为桥梁健康状况评估提供了可行的思路[3-5]。奇异谱分析（SSA）是一种时间序列分析工具，被认为是一种非常成功的数据预处理算法。SSA 可将给定的时间序列分解为有限个更简单和可识别的分量，再将信号按需要进行重组[6-8]，同时它对数据有良好的外推预测能力[9-10]。SARIMA 模型在ARMA 模型的基础上能够有效地对数据中的季节项和趋势项进行处理，避免了现在大多数只使用趋势或者季节性的组合模型的带来的繁琐，在精度方面有着提高[11-12]。因此，基于SSA 分解、重构及外推预测能力和SARIMA 模型，通过工程实例的检验证明组合模型的预测能力比单一模型的预测能力有显著的提升。

1 基本原理

1.1 奇异谱分析

奇异谱分析最早由Colebrook[13]在海洋学研究中提出并使用。SSA 是一种非参数、无模型的时间序列工具，对于时间序列，既不需要假设参数模型，也不需要假设平稳性条件，它可以通过奇异值分解（SVD）将时间序列分解为可分离的分量[14]。在桥梁领域的实际运用中，李小奇等[15]和戴建彪等[16]利用奇异谱分析，分别提取应力监测数据及桥梁索塔GPS 监测数据中的趋势成分和周期成分。SSA 包括时间序列的分解、重构及预测。

（1）分解。原始的时间序列（x1，x2，…，xN）通过映射可以成为K 个长度为L 的向量，定义由这些向量组成的矩阵为轨迹矩阵X

式中，L 是选定的窗口长度，N（N＞2）是时间序列长度，K=N-L+1。对轨迹矩阵X 进行奇异值分解（SVD）可提供L 个特征值、特征向量和主成分的集合。令S=XXT，用λ1，…，λL表示S 的特征值，并假定它们按递减顺序排列，因此λ1≥…≥λL≥0。轨迹矩阵X 的奇异值分解可以写为

其中，Ei=（时间重组序列RCi），Ui为S 对应特征值的标准正交向量，Vi=XTUi/（i=1，2，…，d）。

（2）重构。将初等矩阵Ei的下标i={1，2，…，d}划分成子集I1，I2，…，Im，计I={i1，i2，…，ip}为对应的下标，则有

将式（4）中的每个分组转化成对应长度为N 的时间序列，设Y 为L×K 维矩阵，其元素为Yij（1≤i≤L，1≤j≤K）。令L*=min（L，K），K*=max（L，K），K=N-L+1，则当L＜K 时，Y*ij=Yij，否则，Y*ij=Yji。对角平均按下面公式将矩阵Y 转换成序列g1，g2，…，gN。

式（5）相当于在矩阵对角线i+j=k+1 求平均：当k=1 时，g1=y11；当k=2 时，g2=（y12+y21）/2，以此类推。如果矩阵Y是时间序列（h1，h2，…，hN）的轨迹矩阵，那么对所有i 都有gi=hi。将式（5）应用于式（4）中的EIk（k=1，2，…，m），将形成一个重建序列Z（k）=（z1（k），…，zN（k）），因此，原始时间序列（x1，x2，…，xN）将被分解为m 个时间序列

（3）预测。为了实现SSA 预测，时间序列应该满足线性递归公式（LRF）[10]。时间序列QN=（x1，x2，…，xN）线性递归公式如下

其中gk表示为式（5）重构出来的序列。

1.2 SARIMA 模型

SARIMA 模型，即季节性差分自回归滑动平均，是ARIMA 的发展，并提高了ARIMA 模型在季节性序列建模中的性能。具体内容可参考文献[18]。

2 SSA-SARIMA 组合模型

组合模型预测方法是现在较为热门的方法，一般时间序列数据有三个特性，分别为趋势、周期和噪声。单一预测模型很难同时对三种特性数据有较好的预测能力。因此，采用组合模型成为了提高预测精度的有效手段[4,11,17]，组合模型建立如下：

（1）利用SSA 将原始信号分解为L 个重组序列RC；

（2）引入贡献率和相关矩阵来确定重组的RC 信号组，从而获得趋势、周期和高频三个特征数据；

（3）利用SSA 和SARIMA 模型分别对三种特性数据进行预测；

（4）将预测结果通过评价指标，比较两种模型对三种特征数据的预测效果，并对特征数据拟合度较好的模型进行重组，确定SSA-SARIMA 组合模型；

（5）分别采用该组合模型、SSA 和SARIMA 模型对原始数据进行预测；

（6）采用均方误差（MSE）、均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）等评价指标对预测结果进行比较，验证组合模型的有效性。

上述评价指标的目的是反映模型的预测值与实际值的相似度。预测值越接近实际值，预测误差越小，预测精度越高。在上述四个评价指标中，MES 和RMSE 可以代表结果的总体误差。该值越小，预测结果整体误差越小。MAE 和MAPE 值可以表示为拟合精度。该值越小，说明预测结果精度越高，信号损失越小。

3 实例分析

3.1 数据选取

采用文献[18]中案例验证组合模型的有效性。提取2021 年7 月28 日至8 月28 日的实桥跨中位置加速度传感器数据，由于样本量过大，将每一小时的数据平均值，进行样本量缩减。缩减之后样本量为745 个，大大减少了运算量，加速度数据如图1 所示。

图1 加速度信号

由图1 可知，加速度数据存在明显的趋势和季节性，整体的加速度数据为非平稳数据。由于数据集样本量为745 个，选取前595 个数据为训练集，用作训练模型，后150 个数据为测试集，用作样本外预测，其数据集划分如图2 所示。

图2 训练集与测试集

3.2 SSA 分解与重构

SSA 窗口的长度应尽量为周期的倍数，所以窗口长度为48，SSA 分解结果如图3 所示。由图3 可知，RC1 有着明显的趋势性，RC2-RC3 有明显的周期性，为了更准确地选取趋势项、周期项和高频项，引用贡献率和相关性进行辅助选取。

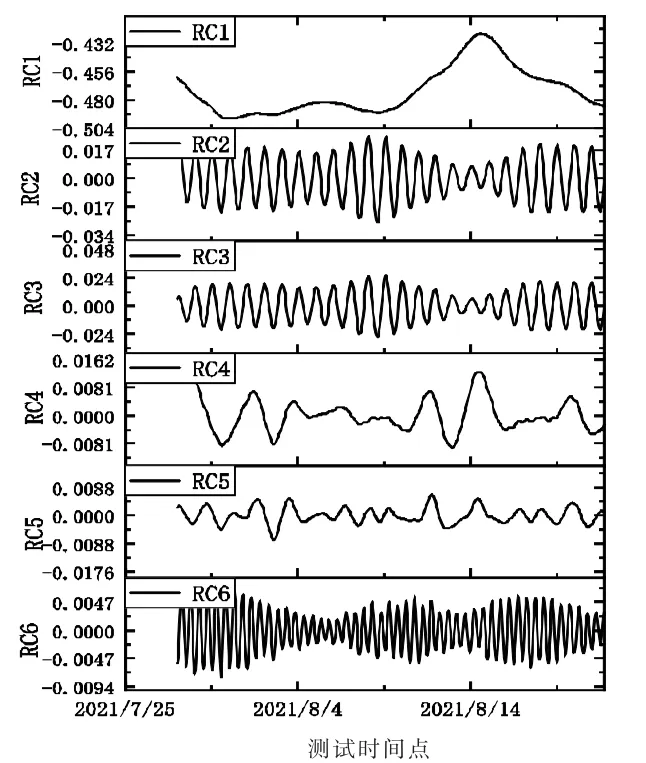
图3 SSA 前6 项分解结果

由图4 特征值对应特征向量的贡献率可以得到，一共有48 个特征值，第1 个奇异值对应RC 的贡献率最大，其占主要成分，第4 个奇异值对应RC 往后的贡献率接近0。再由图5 中RC 相关性矩阵可知，第4 个和第5 个RC 相关性较强，所以最终确定三个分量的划分为：第1 个对应RC 作为趋势项，第2 至第5 个RC 确定为季节项，第6 至第48 个RC 为高频项，组合结果如图6 所示。

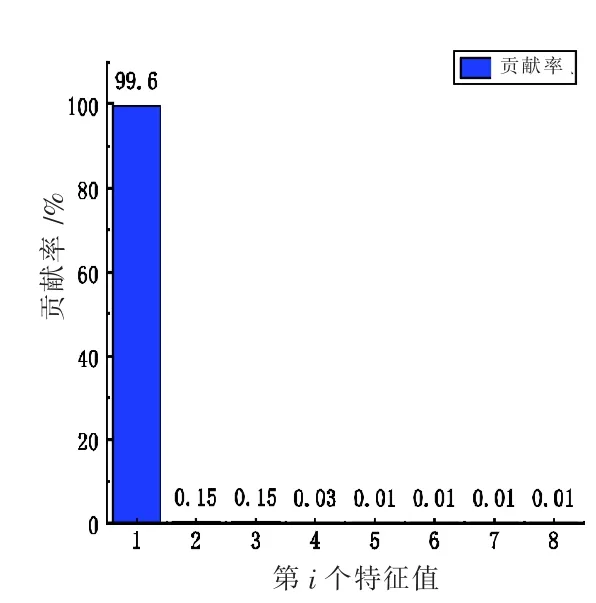
图4 特征值的贡献率

图5 RC 相关性矩阵

图6 趋势项、季节项、高频项重组结果

3.3 选取最优模型

奇异谱分析提取了原始数据的3 个特性分量（趋势、季节、高频）分别利用单一模型对三种特性数据进行预测。图7 为各项预测结果，下面引用MSE 和MAPE 评价指标对模型的误差和精度进行评估，结果如表1 所示。由预测结果可以知道，对于趋势项而言，SARIMA 模型的MSE 和MAPE 值均较小，说明其误差较小，精度较高；对于季节项而言，SSA 模型的MSE 和MAPE 值均较小，说明其误差较小，精度较高；对于高频项而言SSA 和SARIMA 模型的MSE 值均较小，说明两种模型预测误差均小，但是SARIMA 模型的MAPE 值较小，说明其精度较高。所以，最优组合模型选用SSA 模型预测季节项，由SARIMA 模型预测趋势项和高频项。

表1 各分项SSA 和SARIMA 预测结果

图7 趋势项、季节项、高频项预测结果

3.4 单一及组合模型的预测结果

将数据整合，利用原始加速度数据来验证组合模型的预测结果比单一模型的预测结果好。如图8 为原始加速度数据的模型预测结果对比图；表2 为SSA 模型、SARIMA 模型和SSA-SARIMA 组合模型预测效果评价表。从表2 可以看出，对于组合模型，四个指标均小于单一模型，说明组合模型的预测精度要优于其他两种单一预测模型。

表2 各模型预测效果评价

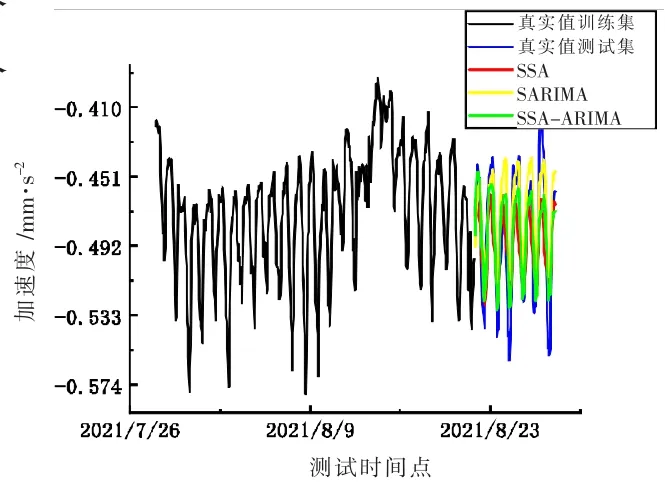
图8 原始加速度数据各模型预测结果对比

4 结语

以某大桥健康监测系统采集的加速度数据为样本，结合SSA 和SARIMA 模型，研究了组合模型在桥梁健康预测分析中的应用。得出以下结论：

（1）基于SSA 的组合模型预测结果能够更为精确的拟合实际结果，为桥梁传感器空缺数据的插补及预测桥梁未来健康状态提供了一个可靠的预测模型。

（2）SSA 分析不仅可以将数据拆分成若干简单含有可识别信息的分量，还可以进行重组提取数据中的趋势分量、季节分量及周期分量，这对于提取桥梁监测数据中的重要信息有着十分重要的帮助。

（3）SSA 模型和SARIMA 模型两种单一模型对于趋势、季节、高频数据的预测能力总体来说较好。但对于桥梁数据而言，高频项数据中往往存在很重要的信息，两种模型对于高频项的误差精度较差，会导致高频能量的丢失。