基于粘弹性边界的三维土体地震响应分析

吴 翔，丁海平

（苏州科技大学 江苏省结构工程重点实验室，江苏 苏州 215011）

工程场地的土层地震反应分析是地震安全性评价工作中的重要组成部分，在进行场地地震反应分析时，土体的动力本构关系、模型尺寸和网格划分、边界条件，以及地震动输入等都是需要考虑的问题。

在通常的土层地震响应分析中，常采用基于一维剪切土层模型等效线性化的波动频域分析方法[1]；对地表地形起伏变化的场地，一般采用二维场地模型的时域线性分析。事实上，土体的非线性对地震响应影响很大。Drucker 和Prager 于1952 年提出了考虑静水压力影响的广义Mises 屈服与破坏准则，被称为Drucker-Prager（DP）准则[2]，后经Sandler、Krajcinovic 等人[3-4]修正后被广泛使用。随着对DP 模型研究的不断深入[5-8]，更符合岩土材料特性的Extended Drucker-Prager（EDP）模型开始被广泛使用[9]。宋宏伟、Luo Chuan 等[10-11]研究了DP 模型和EDP 模型的特点及相互转换问题，证明了EDP 模型的可行性且更符合岩土材料的实际情况。事实上，土体的非线性对地震响应影响很大。巴振宁、梁建文和齐文浩等[12-15]分别对考虑土体线性与非线性、等效线性化与非线性在地震响应中的差异进行了研究分析。本文将依托于大型有限元分析软件ANSYS，以实际工程为背景，建立三维成层土体非线性地震响应分析模型，借助DEEPSOIL 程序实现土体的等效线性化。将对线性模型、等效线性化模型和非线性（EDP）模型的地震响应进行分析，研究土体非线性特性对地震响应的影响。

1 粘弹性边界

在考虑土体的地震响应分析中，核心问题之一是如何正确地模拟无限地基，如采用合适的人工边界。常用的有：无穷边界元法[16]、阻尼提取法[17]和人工透射边界法[18]。本文选择的是粘弹性人工边界[19]。粘弹性人工边界的实质是通过把弹簧和阻尼器设置在每个边界节点上来模拟实际的边界条件。Deeks、刘晶波等[19-20]首先在二维散射波为柱面波的假设下建立了二维粘弹性人工边界，并分析了该边界相对于粘性边界的优势。刘晶波等[21]基于球面波动理论，将粘弹性人工边界由二维平面推广到三维，并通过算例验证了三维粘弹性人工边界的准确性和适用性。本文采用的粘弹性边界参数公式见式（1）。图1 为边界节点三向弹簧-阻尼系统示意图。

图1 边界节点三向弹簧-阻尼系统示意图

其中：KBT和KBN分别为切向弹簧和法向弹簧的刚度系数；CBT和CBN分别为切向阻尼器和法向阻尼器的阻尼系数；R 为波源至各个边界节点的距离；cP和cS为介质的压缩波速和剪切波速；G 和ρ 分别为土层的剪切模量和密度；αT与αN分别为弹簧切向与法向刚度修正系数，参考刘晶波等[22]研究，取值范围及推荐值见表1，本文分别取值为αT=0.67，αN=1.33。

表1 粘弹性人工边界修正系数

通过将地震荷载转化为切向和法向等效节点力的方式实现粘弹性人工边界的模拟，本文施加的等效节点力采用自由场应力法进行推导。具体公式如式（2）所列。

其中，σi（t）为边界上一点i 在t 时刻的等效荷载；σf（x，y，t）为由原自由场产生的应力；k 和c 分别为弹簧刚度和阻尼系数；（x，y，t）和uf（x，y，t）分别为i 点的自由场速度与位移。边界点上施加的等效力通过式（3）计算。

式中，A 为边界点所代表的有效面积。采用公式（3）计算边界节点的等效荷载力。

2 粘弹性边界验证

采用图2 所示的土体模型为算例。模型尺寸为20 m×20 m×10 m，有限元网格尺寸为0.5 m，土体密度为2 000 kg/m3，剪切波速为200 m/s，压缩波速为346.41 m/s，泊松比为0.25。入射波位移函数如式（4）所示；图3为相应的位移时程。由波动理论可知，对于图2 的弹性半空间模型，地表位移的理论值为输入位移的两倍。由图4 可见，地表位移响应的理论解与数值解吻合很好，说明本文采用的粘弹性边界精度良好，可以使用。

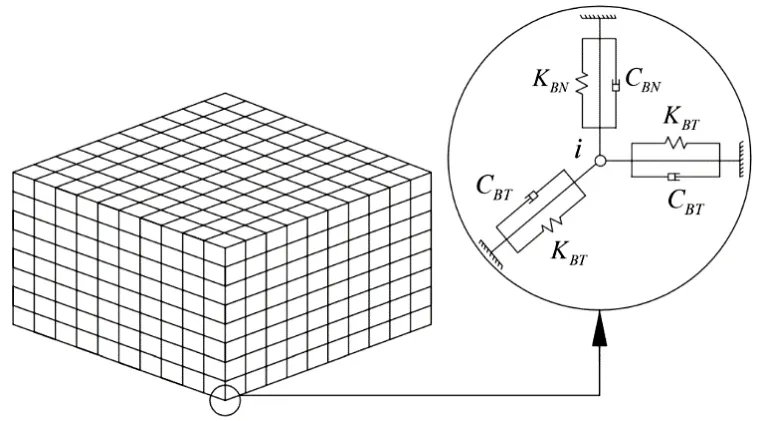
图2 三维土体及粘弹性边界有限元模型

图3 入射波位移时程

图4 地表位移响应的理论解与数值解对比

3 经典DP 模型与扩展DP 模型

3.1 经典DP 模型

在大型有限元分析软件ANSYS 中，DP 模型广泛用于岩石、土体等材料分析中。在使用模拟单元Plane42进行二维实体模拟分析，以及单元Solid45 单元进行三维实体分析的情况下，可以使用经典DP 模型。ANSYS中设定经典DP 模型需要输入3 个参数，即粘聚力、内摩擦角、膨胀角。其中的膨胀角是用来控制体积膨胀的大小的。在岩土工程中，一般密实的砂土和超强固结土在发生剪切的时候会出现体积膨胀，因为颗粒重新排列了；而一般的砂土或者正常固结的土体，只会发生剪缩。所以在使用DP 模型的时候，对于一般的土，膨胀角设置为0°是比较符合实际的。

3.2 扩展DP 模型

EDP 模型作为DP 模型的改进模型[10]，考虑材料的硬化特性，更符合岩土材料的实际情况。在新版本的ANSYS 中，经常使用Solid185 单元替代Solid45 单元，经典DP 模型不能应用在Solid185 单元中，而要采用扩展DP 模型，即EDP 模型。经典DP 模型到EDP 模型的参数需要转换，即通过已知的粘聚力和内摩擦角等计算得到EDP 所需要的参数数值。通过对比经典DP 模型和EDP 模型的屈服函数，发现EDP 模型中的线性屈服函数与DP 模型的屈服函数形式上相似且屈服面形状也相同，通过参数等效替换，EDP 参数的计算公式见下式。

其中，C1为EDP 模型第一个参数，即应力敏感度；C2为EDP 模型的第二个参数，即屈服强度；ϕ 代表土体内摩擦角，C 代表土体粘聚力。

本文使用Solid185 三维实体单元模拟土体，故在考虑土体非线性时，对土体施加EDP 模型。

4 计算模型

4.1 场地条件及土体网格划分

本文选用奥林匹克塔（位于北京市奥林匹克公园）所在位置的场地作为研究对象。土体1/4 模型如图5 所示，尺寸为160 m×160 m×50 m。由下至上依次选取4 个监测点，监测点为每层土体平面中间点，具体坐标如下：A（80，80，0），B（80，80，20），C（80，80，30）和D（80，80，50）)。场地土参数如表2 所示。

图5 土体1/4 模型

表2 场地土参数

在有限元数值模拟中，计算网格的划分对计算结果有明显的影响。网格尺寸过小将导致计算时间过长，同时还会导致计算结果不能收敛，而土体单元过大将导致计算精度不够。因此，合理选择是一个非常重要的问题。一般而言，土体单元高度应符合式（5）和式（6），土体单元的宽度通常可以取高度的2 倍左右[23]

式中，λmin为地震波的最小波长（λmin=Vs/fmax；Vs为土体的剪切波速，fmax为最高频率）。采用的有限元网格尺寸为2 m×2 m×2 m。

4.2 等效线性化模型

本文借助DEEPSOIL 程序，采用等效线性化方法建立等价非线性粘-弹塑性模型，用等效的剪切模量和阻尼比代替不同应变幅值下的剪切模量和阻尼比，将非线性问题转化为线性问题，通过计算得到对应监测点的加速度时域及频域结果。土类动剪切模量比和阻尼比采用袁晓铭[24]的推荐值，如表3 所示。

表3 土样剪切模量比和阻尼比

4.3 地震波的选取

奥林匹克塔的设计基准期为50 年，所处地区的抗震设防烈度为8 度，设计地震分组为第一组，所在场地为Ⅱ类场地，基本地震加速度为0.20g[25]。

入射地震波选取EL-Centro 波，其加速度记录如图6。

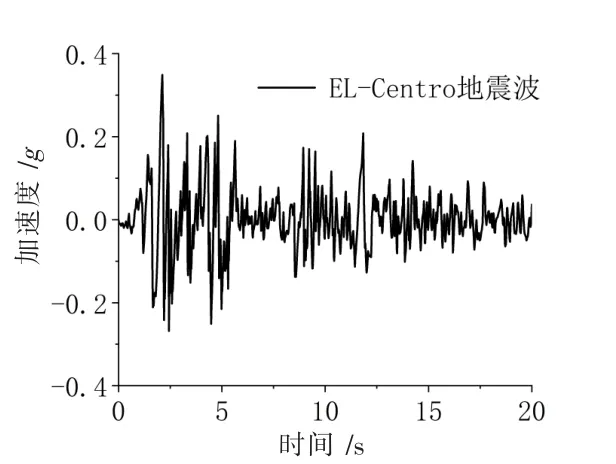
图6 EL-centro 地震波加速度记录

5 计算结果及分析

5.1 位移响应分析

线性模型、非线性模型，以及等效线性化模型各个监测点分别在多遇地震作用下的水平位移响应见图7，设防地震作用下位移响应见图8，罕遇地震作用下位移响应见图9。根据位移时程结果可以得出：（1）在多遇地震作用下，线性、非线性及等效线性化模型的位移响应结果较为接近。这是由于输入地震动强度较小，土体没有完全进入塑性阶段。

图7 多遇地震作用下各模型及监测点水平位移

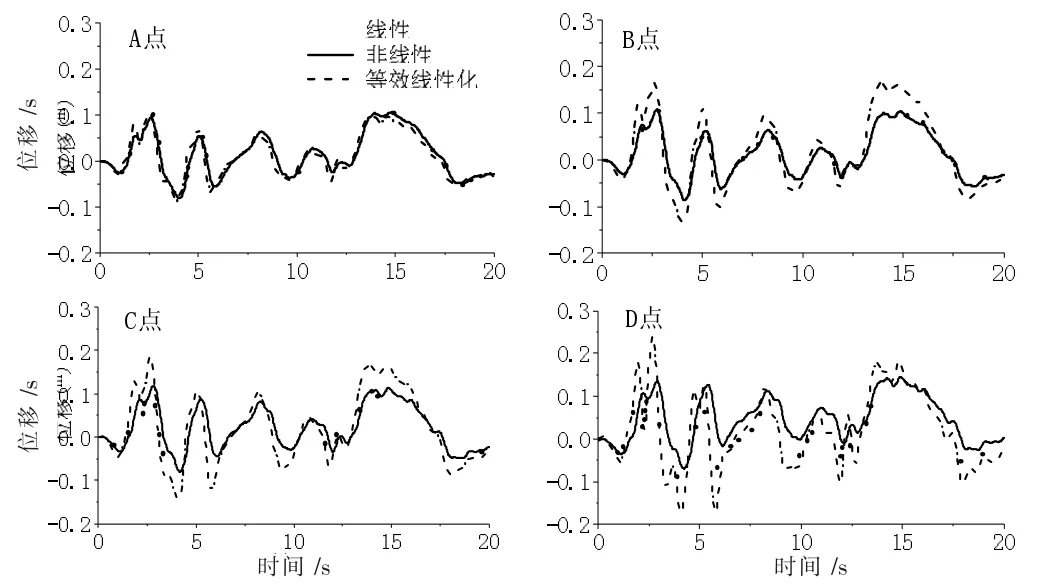
图8 设防地震作用下各模型及监测点水平位移

图9 罕遇地震作用下各模型及监测点水平位移

（2）在设防地震和罕遇地震作用下，对于监测点A 点，线性模型、非线性模型和等效线性化模型的位移较为接近。监测点B 点，C 点和D 点均表现为：等效线性化的位移要明显大于线性和非线性模型；线性模型的位移大于非线性模型的位移。随着土的埋深变浅和地震动强度增加，非线性模型水平位移响应的延迟愈加明显。这是由于土体非线性产生的变形及土体阻尼的增加耗散了一定的地震动能量。

（3）从图7 至图9 可以看出，在多遇地震作用下，线性、非线性和等效线性化的计算结果相似；在设防地震和罕遇地震作用下，等效线性化得到的位移响应显著大于线性和非线性模型，这是等效线性化在地震动输入较大的情况下过高估计了场地土的非线性特性所致。

5.2 加速度时程分析

多遇地震、设防地震和罕遇地震各模型及监测点的加速度时域分析见图10 至图12；为便于对比分析，加速度时域分析取前10 s 的计算结果。从加速度时域结果可以得出：

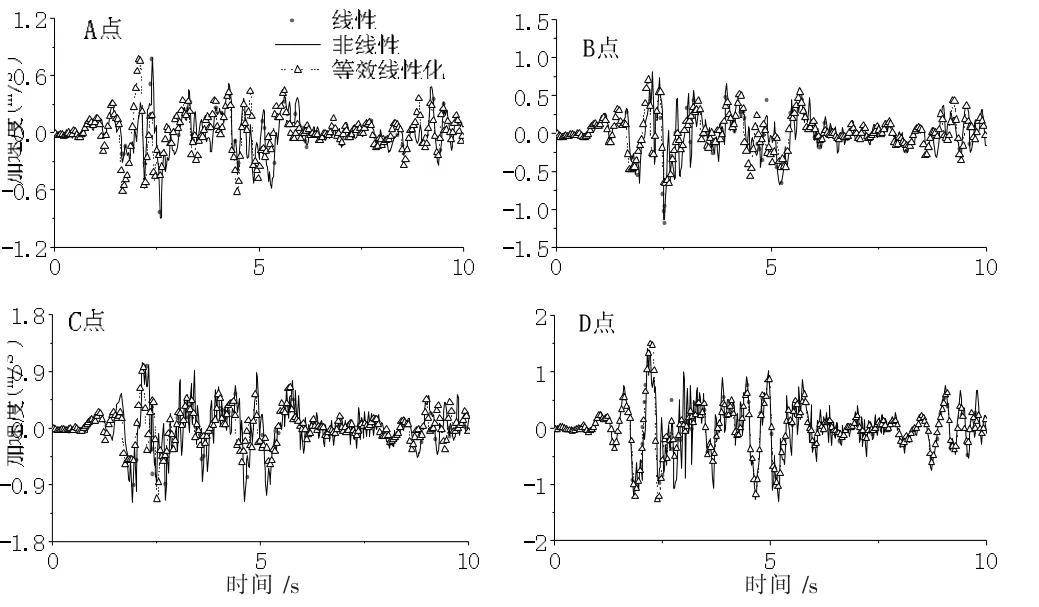
图10 多遇地震作用下各模型及监测点水平加速度

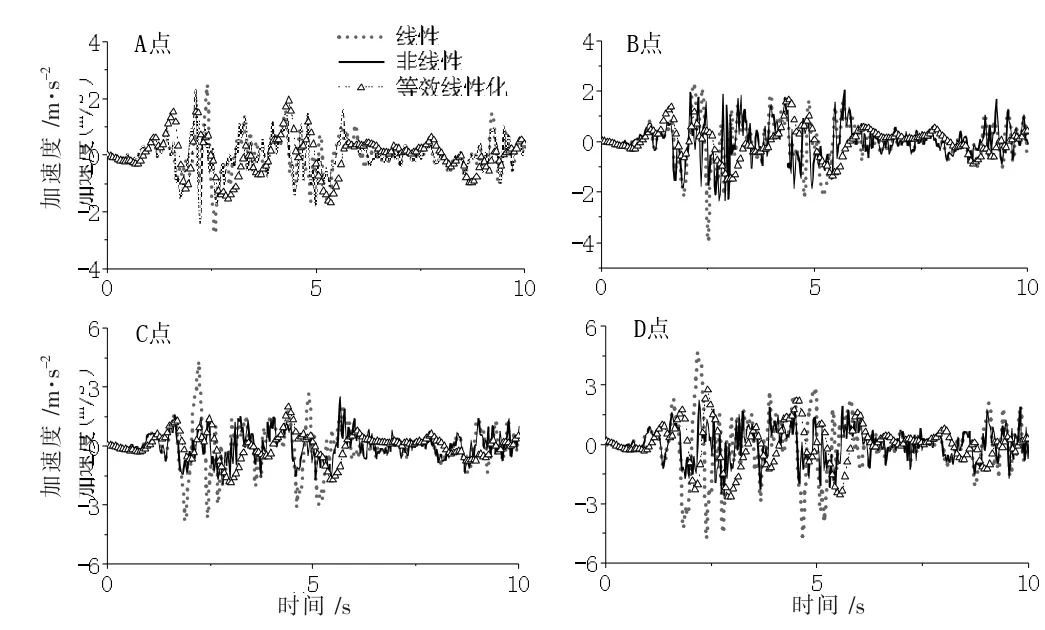
图11 设防地震作用下各模型及监测点水平加速度

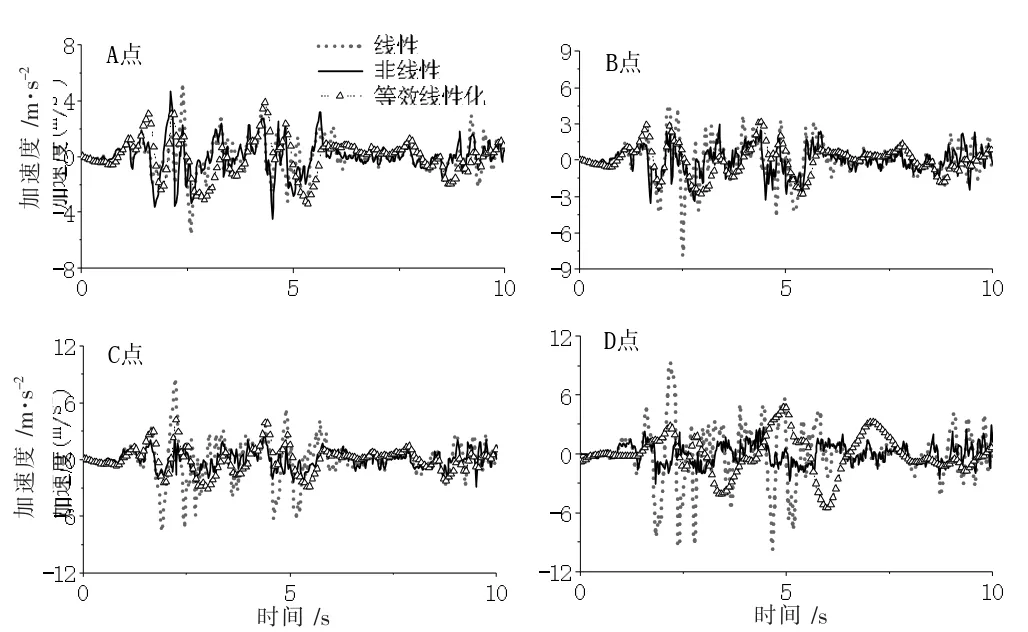
图12 罕遇地震作用下各模型及监测点水平加速度

（1）在多遇地震作用下，线性模型、非线性模型及等效线性化模型的加速度响应总体趋势相同；在加速度峰值方面，非线性模型和等效线性化模型较为接近，二者均小于线性工况下的加速度峰值，这是由于考虑土体非线性后，土体产生的变形及土体阻尼的增加耗散了一定的地震动能量。由于输入地震动强度较小，土体没有完全进入塑性阶段，三种工况下整体区别不大。

（2）在设防地震和罕遇地震作用下，线性条件下的加速度峰值大于非线性条件下的加速度峰值，且随着土的埋深变浅和地震动强度的增大，二者的差值愈加明显，等效线性化的加速度峰值大于非线性条件下加速度峰值。对比多遇地震可见：非线性和线性地震响应存在的差异随着入射地震动幅值的增大而增大。这是由于土体非线性耗散了地震动能量。

（3）从图10 至图12 可以看出，等效线性化得到的加速度峰值与非线性较为接近，但随着输入地震动强度的增加，等效线性化的加速度峰值大于非线性。在输入地震动强度较小的情况下，非线性和等效线性化的计算结果波形相似，在地震动输入强度变大的情况下，二者的差别较大，等效线性化所得的波形变得稀疏。该结论与文献[15]所得结论相同。

5.3 加速度傅里叶谱分析

加速度傅里叶谱见图13 至图15。从加速度频域结果分析可以得出：

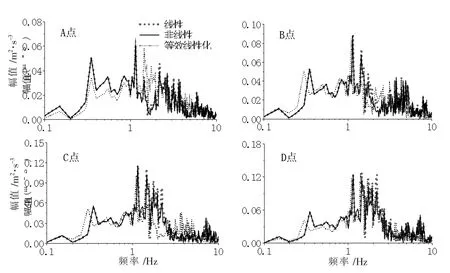
图13 多遇地震作用下各模型及监测点水平加速度傅里叶谱

图14 设防地震作用下各模型及监测点水平加速度傅里叶谱

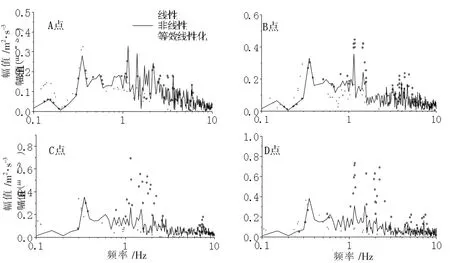
图15 罕遇地震作用下各模型及监测点水平加速度傅里叶谱

（1）在多遇地震作用下，由于土体的滤波效应，非线性和等效线性化的傅里叶谱幅值小于线性模型。等效线性化条件下土体基频降低，图形向左移。由于地震动强度较小，土体没有完全进入非线性阶段，线性、非线性和等效线性化的加速度傅里叶谱总体相差不大。

（2）在设防地震作用下，等效线性化的傅氏谱峰值小于非线性模型，非线性模型的傅里叶谱幅值小于线性模型。在罕遇地震作用下，等效线性化和非线性模型的傅里叶谱幅值远小于线性模型。这是由于土体非线性时模量衰减，基频降低。由于土体的滤波效应，随着埋深变浅，非线性时中高频成分被土体吸收。监测点C和监测点D 非线性和等效线性化条件下的低频显著降低。这一现象是由于地震动输入增大，场地土非线性特性影响增强的结果。这现象与文献[15]所描述规律相似。

（3）等效线性化条件下，土体模量衰减，刚度降低，基频降低，傅氏谱图形向左移了。随着地震动动输入增大，中高频部分快速降低，这是等效线性化在地震动输入较大的情况下过高估计了场地土的非线性特性所致。

6 结论

基于大型有限元分析软件ANSYS 平台及其APDL 编程语言编制了相应的程序，使用EDP 模型考虑土体的非线性特性，施加粘弹性人工边界并验证了其正确性，然后以某实际工程场地为背景对其进行了计算分析，通过与DEEPSOIL 程序得出的等效线性化计算结果进行对比分析，探讨了土体非线性特性对其自身地震响应的影响。基于本文的计算分析，可得如下结论:

（1）当输入地震动强度较小且土体埋深较大时，土的非线性影响不够明显，线性、非线性及等效线性化计算结果相差较小。随着埋深变浅和地震动强度的增大，非线性的位移响应大于线性情况；等效线性化的位移响应显著大于线性和非线性模型。

（2）考虑土体非线性后，土体产生的变形及土体阻尼的增加耗散了地震动能量，随着埋深变浅和输入地震动强度的增加，线性条件下的加速度峰值大于非线性条件下的加速度峰值，非线性条件下的加速度峰值大于等效线性化条件下的加速度峰值，线性计算结果的加速度放大倍数保持不变，非线性计算结果的加速度放大倍数呈递减趋势。能反应“随输入地震动强度增大，土层非线性效应表现越明显”这一基本规律[25]。

（3）在EL-Centro 波作用下，随着埋深变浅和输入地震动强度的增加，土体非线性时模量衰减，刚度降低，低频部分显著降低，同时由于土体的滤波效应，非线性时中高频成分被土体吸收。等效线性化方法虽简单方便，但其往往会过高估计场地土的非线性，因而在地震动输入较大的情况下须谨慎使用。

由此可见，土体非线性特性对其自身地震响应的影响十分显著，在实际工程中使用非线性模型应当考虑土体非线性的影响。