关注学生发展 提升复习效率

[摘 要] 在高三复习教学中,教师要为学生提供机会参与课堂,在参与的过程中通过观察、分析、对比、联想、反思、总结等学习活动发现数学本质、掌握解题方法、积累解题经验,以此发展数学思维,提高自主学习能力,提升高三复习效率.
[关键词] 复习教学;解题经验;复习效率
在高三复习课堂中,部分教师带领学生进行简单的知识梳理后,就将学生带入“题海”,以期借助“题海”实现知识的巩固和强化,提升解题技能,提高解题效率. 但机械重复的练习不仅不能帮助学生积累丰富的解题经验,而且容易造成学生心理负担,影响复习效率. 为了改变这一现状,在习题的设计上应该做到精挑细选,不贪多,不求快,充分发挥例题、习题的引导作用,通过其推广应用来拓展学生的思路,让学生掌握和理解数学学习的方法,以此提升复习有效性[1]. 笔者教学“空间几何体的体积”时,为了更好地发展学生,让学生獲得解题经验,做了一些尝试,取得了一点效果,现分享给大家,以期共鉴.
教学分析
1. 内容分析
求几何体的体积涉及空间点、线、面的位置关系,空间角和距离的数量关系等相关内容,其综合性强,对学生的空间想象能力、逻辑推理能力、数学运算能力、数学综合运用能力的要求较高,是公认的教学难点,同时也是高考的热门考点.
2. 学情分析
本节课内容在新知教学时重点讲解过,并进行过强化训练,因此学生具有一定的解题经验和自主学习能力,以上知识、经验、方法、能力为实现“生本”高效课堂提供了智力支持和精神动力.
3. 教学目标
(1)通过复习求几何体体积的计算公式,帮助学生理解空间几何体体积公式中各个量之间的内在关系,帮助学生建构完善的认知体系.
(2)帮助学生理解并掌握求空间几何体体积常用的方法.
(3)培养学生的空间观念,增强学生的转化和化归意识,提升学生的数学素养.
4. 教学重点
几何体体积的计算.
5. 教学难点
确定几何体的高.
教学实录
1. 知识梳理
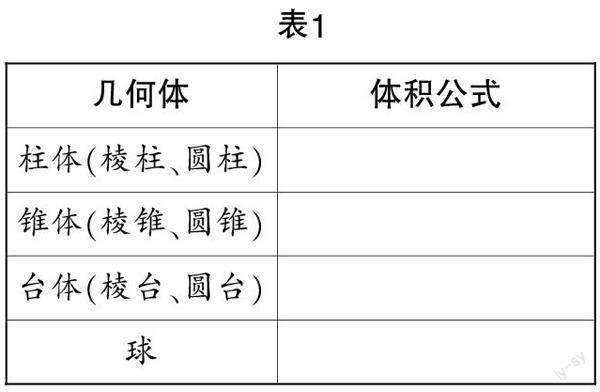
根据导学案要求,学生独立完成表1.
师:课前让大家填写表格,大家都填好了吗?
生齐声答:填好了. (笔者点名让学生回答,并投影展示)
师:仔细观察这些公式,它们之间有什么联系?(学生不语)
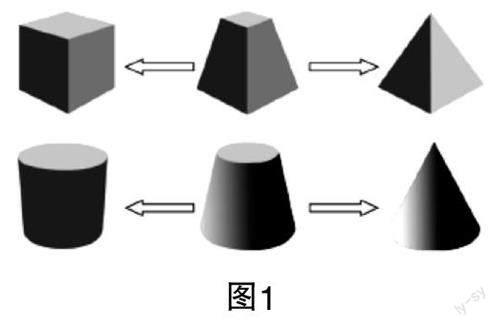
师:结合图1,说一说你有什么发现. (学生积极讨论)
生1:对于棱台,若上底面逐渐扩大,当上底面和下底面全等时,则棱台就变成了棱柱;反之,若上底面逐渐缩小,当缩成一个点时,则棱台就变成了棱锥. 圆台、圆柱、圆锥的变化规律与之相同.
师:说得很好,现在谁来说一说,这些公式有什么联系?(学生跃跃欲试)
生2:对于台体的体积公式,当S=S时,可得柱体的体积公式;当S=0时,可得锥体的体积公式.
设计意图 课前通过表格回顾旧知,唤醒学生的记忆. 课上引导学生结合几何示意图观察柱体、台体和锥体之间的内在关系,以便学生理解和记忆. 同时,借助几何示意图提高学生的直观想象素养,为接下来的解题活动打下坚实的基础.
2. 例题精讲
在复习教学中,为了更好地将知识、方法、经验融合在一起,例题、习题教学必不可少. 不过教师选择例题、习题时切勿贪多、贪新、贪难,应依据实际情况和教学目标合理安排,要确保其具有一定的针对性和目的性,尽量做到一题一得,让每一个学生都能获得不同程度的提升[2].
(1)自然引出“公式法”.
问题1 将一个长为4、宽为2的矩形卷成一个圆柱,求该圆柱的体积.
师:大家可以选择合适的素材,如书、草稿纸等矩形卷一卷,该如何卷,体积如何算?
问题给出后,学生积极操作,很快给出了答案.
生1:以4为圆柱的底面周长,此时圆柱的底面圆的半径为,圆柱的高为2. 根据圆柱的体积公式,可得该圆柱的体积V=πr2h=.
师:很好,和你们的结果一致吗?
生2:这个结果没有问题,但是回答得不够全面,还有另外一种情形.
师:哦,还有一个情形?它的体积是多少?
生2:以2为圆柱的底面周长,此时圆柱的底面圆的半径为,圆柱的高为4,则V=πr2h=.
师:还有补充吗?(学生摇头表示没有补充)
师:很好,通过动手操作我们发现了圆柱的两种不同形状,并利用圆柱的体积公式直接求出了其体积.
师:若为以上求体积的方法起个名字,你们感觉应该叫什么?
生齐声答:公式法. (笔者板书)
练习1 图2是一个六角螺帽,它由一个正六棱柱挖去一个圆柱构成. 已知正六棱柱的正六边形底面边长为2 cm,高为2 cm,内孔半径为0.5 cm,则六角螺帽的体积是____cm3.
题目解析 本题主要考查学生利用“公式法”求柱体的体积. 正六棱柱的体积V=6××2×2×sin60°×2=12(cm3),圆柱的体积V=π×0.52×2=(cm3),两者相减即可得六角螺帽的体积.
设计意图 通过具体操作,提炼解题方法,进一步加深学生对“公式法”的理解.
此环节主要以学生自主探究为主,让学生通过具体操作体验解题过程,提炼解题方法. “公式法”起点低,易于学生理解和接受,可充分调动学生参与探究的积极性,激发学生的学习动机,为接下来进一步探究创造条件.
(2)合作探究“等体积法”.
问题2 如图3所示,平面ADE⊥平面ABCD,△ADE是边长为a的等边三角形,四边形ABCD为矩形,F为AB的中点,EC与平面ABCD所成的角为30°,求三棱锥F-CDE的体积.
问题2的难度略有提升,不能用“公式法”直接求解,需要学生另寻他法. 问题2给出后,笔者预留时间让学生独立思考,接下来通过互动交流逐渐引出“等体积法”.
师:谁来说一说,解题时你遇到了哪些问题?
生3:求三棱锥F-CDE的体积需要知道它的底面积和高,△CDE的面积易求,但是点F到平面CDE的距离怎么求呢?
生4:开始我和生3的想法一样,也想直接利用“公式法”求解,遇到了同样的困惑. 但仔细分析后发现,三棱锥F-CDE与三棱锥E-CDF是同一个三棱锥,这样可以将求三棱锥F-CDE的体积转化为求三棱锥E-CDF的体积. 又△CDF的面积为a2,这样只要求出点E到平面CDF的距离即可. 由已知条件“平面ADE⊥平面ABCD”,取AD的中点H,连接EH,EH就是点E到平面CDF的距离(可证). 根据已知条件易求EH=a,故V=V=·EH·S=a3.
师:很好!生4将不易于求高的三棱锥转化为易于求高的三棱锥,问题便迎刃而解. 若为这一方法命名,你们觉得叫什么比较合适呢?
生5:等体积法. (笔者板书)
师:若将“三棱锥”改为“四棱锥”“五棱锥”,这种方法是否依然适用呢?(学生陷入沉思)
生6:不行,对于其他棱锥,若将顶点换掉,则其他顶点不共面.
师:很好,分析得很到位,看来“等体积法”在锥体体积计算中只适合三棱锥. (笔者在板书“等体积法”后加上条件:适合三棱锥)
师:思考一下,点F到平面CDE的距离是否可求呢?
生7:可以,可根据“等体积法”求解.因为V=V(已求),这样只要求出△CDE的面积,即可求出点F到平面CDE的距离.
师:很好,这样通过“等体积法”不仅能求出三棱锥的体积,还能求出点到平面的距离,可见这是求点到平面的距离的重要方法之一.
设计意图 通过精选例题,创设障碍,诱发学生探索不同的解题路径,培养学生思维的灵活性和变通性. 学生顺利求解后,笔者继续追问,诱发其深度思考,总结归纳出“等体积法”的适用范围,并通过问题推广让他们发现求点到平面的距离的重要方法,发挥了问题的最大功效.
练习2 如图4所示,已知正方体ABCD-ABCD的棱长为a,点E,F分别为棱AA和CC的中点,求四棱锥A-EBFD的体积.
题目解析 EB=BF=FD=DE=a,连接EF,则△EFB≌△EFD. 由于三棱锥A-EFB与三棱锥A-EFD等底同高,因此V=2V=2V. 这样只要求出三棱锥F-EBA的体积,问题便可迎刃而解.
设计意图 在复习教学中,教师应多一些引导,少一些灌输,多为学生创造一些时间和空间去交流、去发现,以此激发学生主动探索的热情. 对于问题2,大多数学生从“公式法”出发,但在求点到平面的距离时受阻,这样通过“障碍”点燃了学生探究的热情,使学生得到了求体积的另一种方法——“等体积法”. 接下来通过追问,进一步强化学生对“等体积法”的理解,让学生明晰该方法的适用条件,有效避免解题时盲目套用方法所带来的错解风险,最终培养学生思维的深刻性.
(3)自主探索“补形法”.
问题3 在三棱锥A-BCD中,侧棱AB,AC,AD两两垂直,且长度分别为1,,2,则三棱锥A-BCD的外接球的体积为________.
生8:由于三棱锥的侧棱两两垂直,将三棱锥补形成长方体,则三棱锥的外接球与长方体的外接球相同,这样问题就转化成了求长方体的外接球的体积. 而长方体的体对角线为球的直径,于是有(2r)2=12+()2+22=8,故r=. 根据球的体积公式,易得V=π.
师:非常好. 根据已知条件将三棱锥转化为易于求解的长方体,通过化归与转化,轻松地解决了问题. 这个方法叫什么呢?
生齐声答:补形法. (笔者板书)
练习3 在三棱锥A-BCD中,侧棱AB,AC,AD两两垂直,△ABC,△ACD,△ADB的面积分别为,,,则三棱锥A-BCD的外接球的体积为________.
题目解析 将三棱锥A-BCD补形为长方体,设长方体的三边为a,b,c,由题意得ab=,ac=,bc=,解得a=,b=,c=1,故外接球的直径为=,因此三棱锥A-BCD的外接球的体积为π.
设计意图 让学生理解“补形法”,并熟练应用“补形法”解决问题. 同时,借助“补形法”培养学生的空间意识,提升学生的直观想象素养.
(4)交流探讨“分割法”.
问题4 如图5所示,已知三棱锥P-ABC中,棱长AC为6,其余棱长均為5,求三棱锥P-ABC的体积.
有了前面的解题经验,在此环节中,笔者组织学生交流讨论,共同探寻解题方法.
师:谁来分享一下解题过程?
生9:如图5所示,因为PA=PB=PC=5,所以顶点P在底面的射影为△ABC的外心,设其外心为O,则PO为三棱锥P-ABC的高. 在等腰三角形ABC中,其外心O在AC的中垂线上,且点O在△ABC的内部. 设OA=r,则r2=32+(4-r)2,解得r=. 所以OP==,故V=·S△ABC·PO=×12×=.
师:很好,利用“公式法”解决了问题,思路清晰、严密. 除了“公式法”外,你还有没有其他发现呢?
生9:可以通过拆分三棱锥P-ABC求其体积.
师:具体说一说.
生9:取AC的中点D,因为△PAC和△ABC都是等腰三角形,易得AC⊥平面PBD,则截面PBD将三棱锥P-ABC分成了两个共底的三棱锥,分别为三棱锥A-PBD和三棱锥C-PBD. 于是V=V+V=·AD·S+·CD·S=×6×S=2S. 又PB=5,BD=PD=4,所以S=. 所以V=.
师:非常好,通过分割优化了解题过程,提高了解题效率.
师:对于这种方法该如何称呼呢?
生10:分割法. (笔者板书)
设计意图 通过对比交流让学生知道恰当的“分割”可以简化运算过程,提升解题效率. 同时,通过多解发散学生的思维,培养学生的灵活应变能力.
3. 课堂小结
师:今天我们重点研究了什么?你有什么收获?
生11:重点研究了多面体的体积计算.
生12:复习了四种重要的体积计算方法.
……
师:很好,其实解题方法是灵活多变的,解题时我们要根据已知条件合理选择方法,灵活转化,从而提高解题效率.
设计意图 通过知识梳理,帮助学生进一步巩固知识和方法,以及建构完善的认知体系.
教学思考
在高三复习教学中,部分教师将主要精力放在知识重现和解题技巧的讲授上,忽视了学生数学解题经验的积累. 为了“求多”“求快”,这部分教师只关注“如何教”,忽视了“如何学”,从而限制了学生发展,影响了复习. 在本节课的教学中,为了更好地发展学生,提高复习教学的有效性,笔者做了如下尝试:
首先,为学生提供了参与课堂的机会. 在本节课的教学中,无论是基础知识梳理,还是问题精讲,抑或是课堂小结,都是先由学生独立思考,再进行沟通交流,让学生正确认识和理解知识,发现知识间的内在关系,总结规律,形成方法.
其次,帮助学生积累解题经验. 在解题教学中,笔者坚持“以生为本”,引导学生通过观察、对比、讨论、归纳、反思等活动发现知识与问题、结论之间的联系,利用已有知识、经验探索解决问题的方法,发现解决问题的一般策略. 在教学中,笔者鼓励学生应用不同方法求解,以此拓宽学生的解题视野,丰富学生的解题经验.
最后,关注教学实效. 在教学中,笔者“不贪多”“不求快”,充分挖掘问题的拓展功能,力求让学生每解一个问题都有不同的收获,有效避免简单重复所带来的枯燥感,激发学生的数学学习信心.
总之,在教学中,教师要精心设计教学活动,及时组织学生总结和反思,通过有效反思、回顾、頓悟,认清数学的本质,提炼解决问题的方法,以此提升解题效率.
参考文献:
[1] 佘世庆,佘元振. 基于“数学核心素养”视角下的高三复习课课例研究[J]. 数学学习与研究,2021(08):2-3.
[2] 曾荣. “微专题”复习:促进深度学习的有效方式[J]. 教育研究与评论(中学教育教学),2016(04):28-34.
作者简介:吕永玉(1987—),本科学历,中学一级教师,从事高中数学教学工作.

