市场法评估企业绩效评分中价值比率调整方法的优化

■ 周鹰飞 胡 兵 俞家清 徐太生

（1.江苏华信资产评估有限公司，江苏南京 210000；2.江苏省资产评估协会，江苏南京 210000）

一、引言

在评估实务中有一类具有“专精特新”特质的企业，它们在评估基准日收入少（或者无）、利润少（或者为负）、资产总额也小。如何合理地采用市场法对它们进行价值评估成为评估实务中的一个难点。本文选用“EV/资本”价值比率作为衡量企业价值的倍数，并采用企业绩效评分计算得出各可比公司及被评估企业的总分值，传统方法是直接将被评估企业总分值除以可比公司总分值，得出各可比公司价值比率的调整系数，然后利用该系数计算得出调整后的价值比率，取其平均值作为被评估企业的价值比率，再据此计算被评估企业的价值。采用该方法在评估实务中，我们发现由于选取可比公司数量的不同，或者一组可比公司价值比率上下波动范围的不同，计算得出的被评估企业价值比率变动可能很大，即价值比率的稳定性不足，从而影响被评估企业价值的合理性和有效性。

本文选取科源制药（301281.SZ）作为被评估企业，以一组化学制药的上市公司为可比公司，分别就股票市场的定价与上市公司比较法估值进行分析，针对价值比率和公司总分值（公司得分）两个参数，研究表明采用最优尺度回归确实比直接价值比率对比调整具有更小的误差范围，从而实证说明该方法的有效性。

二、企业绩效评分

企业绩效评分是借鉴《企业绩效评价标准值2023》中的评价指标体系和评分标准，并结合企业所属行业的特点，从企业的盈利能力、资产质量、债务风险、经营增长等方面对被评估企业与可比公司间的差异进行量化，选取适宜的财务指标按照功效系数法计分原理，将评价指标实际值对照行业评价标准值，按照规定的计分公式计算各项基本指标得分。再在基本指标计分结果的基础上，运用功效系数法原理，分别计算盈利能力、资产质量、债务风险和经营增长四个部分的综合修正系数，再据此计算出修正后的分数（图1）。基本计算公式如下：[1]

图1 财务指标的总得分计算逻辑示意图

单项基本指标得分=本档基础分+调整分

基本指标总得分=∑单项基本指标得分

各部分修正后得分=各部分基本指标分数×该部分综合修正系数

修正后总得分=∑各部分修正后得分

三、价值比率的选择与确定

价值比率是指在资产价值和与其具有关联关系的财务或者非财务等指标之间所建立的比值关系，并以此作为评估资产价值的一种价值倍数。[2]按照价值比率的分母分类可以是盈利类指标、收入类指标、资产类指标，针对不同类型的指标可以衍生出不同类型的价值比率，如盈利类指标衍生出盈利基础价值比率；资产类指标衍生出资产基础价值比率等。[3]

当被评估企业处于成长期或高投入期时，其收入少（或者无）、利润少（或者为负）、资产总额也小。现有的价值比率不能准确地衡量企业的价值，因此，本文采用公司资本（股本+资本公积-库存股）作为价值比率的分母，重新定义一个新的价值比率，即“EV/资本”。

企业价值（EV）=20 日成交均价×A 股股本+付息负债+少数股东权益价值+优先股价值-非经营性资产（扣除负债），货币资金并入非经营性资产计算。

科源制药于2023 年4 月4 日登录中国A 股创业板，公司主要从事化学原料药及其制剂产品的研发、生产和销售，产品覆盖降糖类、麻醉类、心血管类及精神类等领域，同时兼营少量中间体业务。因此，本文选择申银万国三级行业分类中的原料药、化学制剂和其他生物制品中的全部股本为A 股的上市公司作为可比公司。以2023 年6 月30 日为评估基准日共选择出162 家，计算出各价值比率和公司得分（表1）。

价值比率种类众多，对于价值比率的最佳估计常常是通过运用最适合的价值比率得出。[4]本文采用统计方法，把各种价值比率与公司得分进行相关分析，以相关系数最高的价值比率作为最佳解释价值比率，即“EV/资本”价值比率（表2）。EV/IC、EV/EBIT、EV/S 因相关系数为负值，不符合经济预期，不适用。

四、可比公司

我们以公司得分为纵坐标，“EV/资本”价值比率为横坐标作图，观察公司得分与价值比率间的分布。基于各家公司得分相近，则它们的基本经营绩效情况相似、公司价值相近的判断，理论上各家公司应该沿着图中右下向左上分布（图2）。但股票市场会受到无效性因素的干扰影响，个别股票价格可能会有一些非正常的异动，实际结果并非如此，测算的拟合优度非常小，R2为0.083。

图2 可比公司分布分散，存在着强影响点

为此，我们对可比公司价值比率较高值端数据进行5%截尾处理，以减轻极端值的影响，排除极端值后拟合优度略有改善，R2为0.111。但分布情况并未改善，按上市板块分类观察，与科源制药（被评估企业，图中标注1）公司得分0.8903 相近的可比公司，3 个板块均有，以创业板上市公司居多，但价值比率分布范围较宽（图3）。如按细分行业分类观察，同样是3 个细分行业均有，以化学制剂公司居多，价值比率分布范围同样较宽（图4）。

图3 与科源制药公司得分相近的可比公司，以创业板上市公司居多

图4 与科源制药公司得分相近的可比公司，以化学制剂公司居多

五、价值比率调整

为了稀释个别股票价格的异动，传统可比公司数量的选择可以以被评估企业得分为基础，以接近被评估企业得分附近的一组公司作为可比公司。我们选取与科源制药公司得分差异率在±9.5%的公司作为可比公司（共29 家），计算价值比率调整系数和调整后的价值比率，取其平均值作为科源制药的价值比率（表3）。

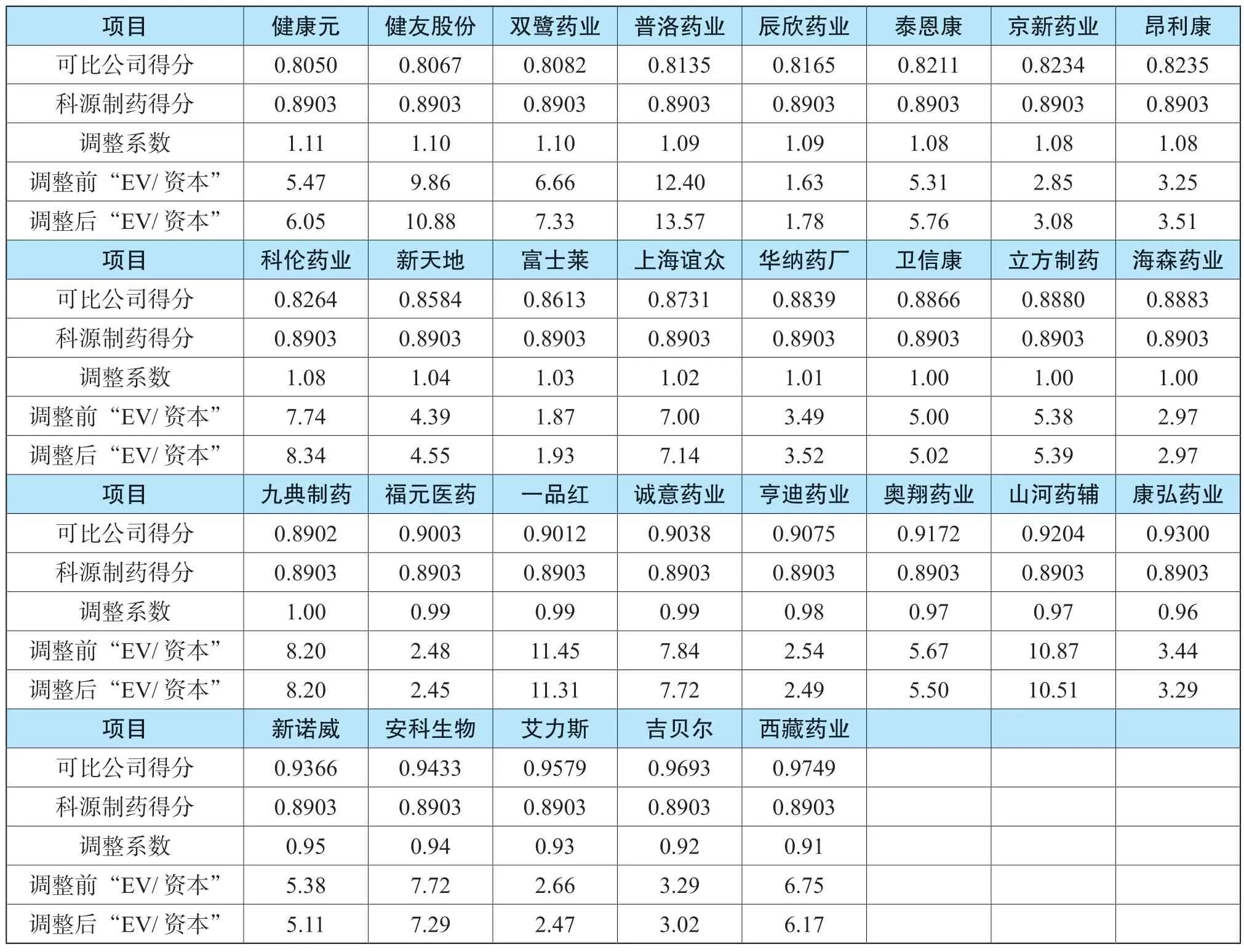
表3 价值比率调整计算

调整后“EV/资本”的平均值为5.74，股票市场对科源制药的定价为4.43，两者差异率为29.6%。产生差异的主要原因是由于价值比率分布范围较宽所致（图3、图4）。减少可比公司数量，或者从提高可比公司信息质量入手选择可比公司，可能价值比率的计算结果有所改善。受可比公司信息收集所限，在未能深入理解可比公司价值内涵的基础上，对可比公司选择一般是以价值比率为基础进行数据双边截尾处理。妥善处理可比公司数量与质量之间的矛盾，成为实务操作过程难点之一。选择不同数量的可比公司计算价值比率平均值，其数值可能存在变动较大、不稳定的问题。

六、价值比率调整方法的优化

（一）最优尺度回归

将被评估企业得分与可比公司得分直接相除，即意味着公司得分之间的差距是相等的或者说它们对价值比率的数值影响程度是均匀的，这种假设有些草率，基于此的分析有时会得出很不合理的结论。公司得分与价值比率之间并不存在一种函数或确定性依赖关系，它们之间是一种统计依赖关系。这个性质的意义在于：公司得分固然重要，但并不能准确地预测公司价值比率。依据计量经济学原理，一则对公司得分和价值比率的测量不论多么精细，总是存在着测量误差；二则除了公司得分外，还有一大堆整体影响着价值比率的因素，却难于一一辨认出来。因此，无论我们考虑了多少个影响因素，却无法完全地解释价值比率。它的一些“内在”的或者随机的变异是注定存在的。[5]也就是说，我们需要采用计量经济学原理处理随机变量。

在统计学中，按照对事物描述的精确程度，将所采用的测量尺度从低到高分为4 个层次：定类尺度、定序尺度、定距尺度和定比尺度。在这4 种测量尺度之间，按照信息量的高低，可将高层次测量尺度的测量结果转换为低层次测量尺度的测量结果。[6]因此，我们将公司得分的测量尺度由定比更改为定序尺度，但更改后其计量结果只能自然排序，不能直接进行算术运算。为此，我们首先进行最优尺度变换。可在SPSS 统计软件中使用分类回归（Categorical Regression）过程实现。

最优尺度变换是专门用于解决在统计建模时如何对变量进行量化评分的问题，其基本思路是基于希望拟合的数学模型框架，分析各级别对因变量影响的强弱变化情况，在保证变换后各变量间的联系为线性的前提下，采用一定的非线性变换方法进行反复迭代，从而为原始自变量的每一个类别找到最佳的量化评分，随后在相应模型中使用量化评分代替原始变量进行后续分析，这样就可将各种传统回归分析方法的适用范围一举扩展到全部测量尺度。如果最优尺度变换技术被用于线性回归，即最优尺度回归方法。[7]

我们采用SPSS 的分类回归对变量进行变换，为每一个变量用量化评分的方式来表示各类变量间的差异，评分近似则表示影响程度相近，评分相差越大影响程度差异也越大。公司得分（表4）和价值比率（表5）经“最优尺度变换”后得到原始变量和量化评分的对应量化数值表。

表4 公司得分a

表5 EV/资本a

（二）模型假设检验

最优尺度回归的本质是基于模型效果最优化的原则，首先对原始变量进行变换，将各变量转换为适当的量化评分，然后使用量化评分代替原变量进行回归分析，因此结果输出基本上都是变换后评分的分析结果。[7]

从表6 模型摘要给出的结果可知模型的拟合优度略低，变换后模型的调整后决定系数为0.109。对于经济数据，在针对市场法评估进行的回归分析中，我们没有必要强调多高的R2才有意义，相反，我们更应该强调回归分析本身的预测能力。当R2下降时，回归的预测范围将会扩大。[8]

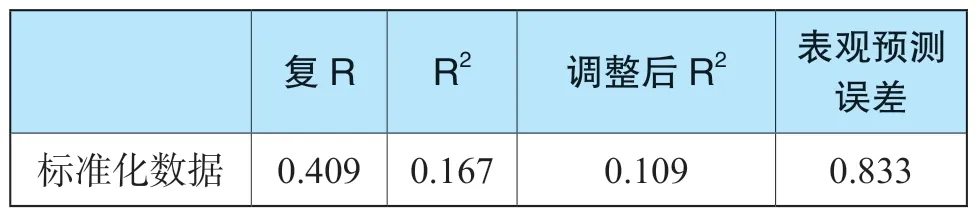
表6 模型摘要

表7 是总模型有无意义的检验。结果表明变换后评分拟合的模型整体非常显著，P 值为0.003，模型具有统计学意义。

表7 方差分析（ANOVA）

表8 为模型中系数的估计值和检验结果。P 值小于0.001，结论为公司得分的量化评分和“EV/资本”的量化评分间的联系有统计学意义。

表8 模型中变量系数

总体结论：模型总体通过了统计学检验，拟合变换后评分数据显著，公司得分的量化评分通过了统计学检验，公司得分的量化评分和“EV/资本”的量化评分之间关系符合经济学预期。

（三）被评估企业价值比率的确定

被评估企业价值比率的确定过程分为三个步骤：

第一步，根据“公司得分”量化表采用插值法计算被评估企业公司得分的量化评分。被评估单位公司得分原始值为0.8903，计算出的量化评分为1.0000。

第二步，由被评估企业公司得分的量化评分1.0000 计算出被评估企业价值比率的量化评分为0.4090（1.0000×0.4090）。

第三步，对照“EV/资本”量化表采用插值法计算，将被评估企业价值比率的量化评分转换成变换前价值比率的原始数值，即反推计算出评估对象的价值比率。即得到：EV/资本=4.41。

股票市场对被评估企业（科源制药）“EV/资本”的定价为4.43。二者比较，差异率为0.45%。

七、价值比率稳定性的研究

如图5 和图6 所示。因为我们把“EV/资本”设定为等距的数值变量，SPSS 只是对它进行了标准变换，在变换中没有改变各数据间的差异（图5）。

图5 “EV/资本”评分对应图

图6 “公司得分”评分对应图

由图6 观察发现，各可比公司可以分为若干组，同一组内可比公司被赋予了相同的量化评分，不同组之间的可比公司的量化评分则不同，有的组之间差距还非常大。随后的回归分析就是用变换后的分值进行，相当于评分间为等距变化。

在上文介绍最优尺度变换时，“基于希望拟合的模型框架，分析各级别对因变量影响的强弱变化情况”。显然，最终的量化评分会受到希望拟合的模型的影响，变换仅仅保证相应的量化评分在当前模型框架中为最优，如果模型发生改变，比如说引入了新的自变量，或者其他变量的测量尺度进行了更改，则量化评分的结果也会发生改变。[7]本文通过排秩对可比公司个案等级排序来对变量进行离散化处理，样本量的变化同样影响量化评分的结果。为研究相应评分的准确和稳定，即模型的稳定性。我们以价值比率为基础将可比公司组内公司数量分别从最高或最低或同时减少，观察模型的稳定性（表9）。研究表明：总体来看，在样本量较多的情况下，模型相对稳定。

八、总结

1.由于资产评估中采用的经济数据为观察（非实验）数据，不管是价值比率还是公司得分或者其他参数测量总是存在测算误差，通过计量经济学原理分析，回归方程能够很好地对数据进行处理和解释。

2.最优尺度回归也可应用于多元回归分析。对于影响价值比率的因素除了公司得分外，还可以加入研发费用等等其他指标。实际上其应用范围不仅限于回归，可以用于任何多变量模型和多元模型框架。

3.本文对价值比率调整方法提出采用最优尺度回归优化进行了初步探讨，并对其使用方法进行了介绍。对可比公司价值比率调整方法采用最优尺度回归，极大提高了被评估企业价值比率计算的合理性和稳定性，在评估实务中具有应用意义。