具有竞争机制的觅食者-掠夺者模型的高维空间有界性分析
刘洪燕,刘丹丹,江利情,蒋 敏
(贵州民族大学 数据科学与信息工程学院,贵阳 550025)
近年来,对多物种或多化学信号的趋化模型推广在数学生物学领域引起了极大关注,例如Tao等[1]提出的觅食者-掠夺者模型:

(1)
其中,x表示觅食者、掠夺者、食饵所在的位置,t表示时间,u=u(x,t)、v=v(x,t)、w=w(x,t)分别表示觅食者、掠夺者、食饵的种群密度,-λ(u+v)w表示食饵的消耗,非负函数r=r(x,t)表示食饵的生产率,参数χ1、χ2、λ、μ分别表示趋化项系数(觅食者被食物吸引、掠夺者跟随觅食者、2组动物都在随机扩散、乙组动物在接触时消耗营养),食饵消耗率以及食饵自身死亡率均为正,主要研究当空间维数n=1时模型(1)经典解的全局存在性和一致有界性;接着,在高维空间中,Wang等[2]通过对初始数据以及参数进行限制得到了模型(1)的有界性。除此之外,Cao等[3]和Liu[4]研究了拟线性觅食者-掠夺者模型经典解的存在性和有界性。对于具有奇异性、非线性项或者非线性扩散项的觅食者-掠夺者模型的研究,可以参考文献[5-7]。这类模型可以用来描述剪水鹱通过追踪三趾鸻寻找食物的过程,在生物学和生态学上有着广泛的应用。但是,以上研究都没有考虑到带竞争机制的觅食者-掠夺者模型,所以Wang等[8]考虑到这一点,研究了带有竞争机制的觅食者-掠夺者模型:
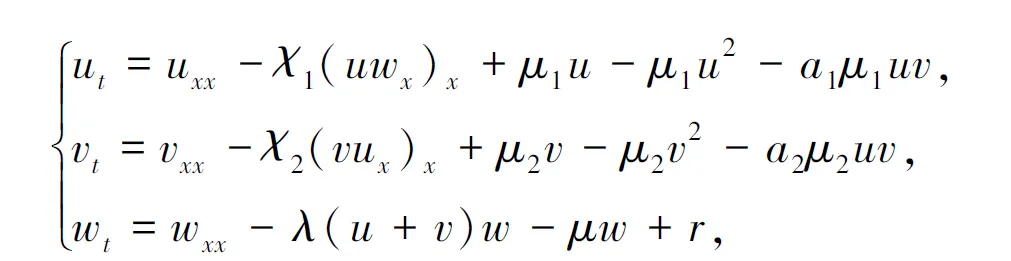
(2)
其中,μ1u、-μ1u2、-a1μ1uv分别表示觅食者的增殖、死亡、竞争,μ2v、-μ2v2、-a2μ2uv分别表示掠夺者的增殖、死亡、竞争,第1种趋化机制-(uwx)x表示觅食者向食饵梯度增加的方向移动,而掠夺者则跟随觅食者去寻找食饵(对应第2种趋化机制-(vux)x),Wang等证明了模型(2)解的全局有界性以及大时间行为。
结合以上分析可知,对含有竞争机制的觅食者-掠夺者模型,已有文献都没有对高维空间进行研究,基于此,研究在高维空间中具有竞争机制的觅食者-掠夺者模型:

(3)
χ,ξ,λ,μ,a1,a2,b1,b2,δ1,δ2>0和α,β>1;
(4)
初值(u0,v0,w0)满足
(u0,v0,w0)∈(W2,∞(Ω))3和u0,v0,w0≥0;
(5)
非负函数r满足

(6)
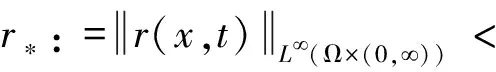
(7)
则有如下主要结果:
定理1设Ω⊂n(n≥3)为具有光滑边界的有界域,假设r满足式(6)(7),p>n/2+1,(p表示p次幂可积),且式(4)成立。若
(8)
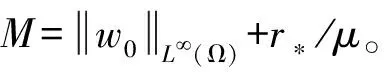

此外,存在常数C>0使得对任意t>0,有
(9)
在下文中,对时间t在空间Ω上的积分符号dt均省略。
1 准备工作
在证明主要结果之前,先给出模型(3)经典解的局部存在性。
引理1[9]假设Ω⊂n(n≥3)为具有光滑边界的有界域,式(5)(7)成立,则存在时间的最大值Tmax∈(0,∞]使得模型(3)存在唯一非负经典解对任意t>0,满足u,v,w>0。此外,若Tmax<∞,则有∞。
下面给出证明定理1需要用到的一些重要的引理。
引理2[1]假设引理1的条件成立,则对任意t∈(0,Tmax),模型(3)的解满足
(10)
引理3假设引理1的条件成立,则对任意t∈(0,Tmax),模型(3)的解满足

(11)


(12)
该引理的证明可以参考文献[7],此处省略其详细的证明过程。

y(t)≤max{y(0)+C2,(C2/C1τ)+2C2}。
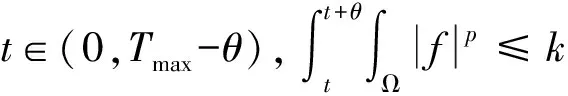
其中,z0满足z0∈W2,∞(Ω),z0>0,且在∂Ω上∂νz0=0,则存在常数C>0,使得t∈(0,Tmax-θ),
成立,特别地,存在常数C*>0使得函数z满足
2 解的有界性及定理1的证明
本节将给出(u,v,w)的有界性证明,并由此证明定理1。
引理6设p>1并且式(5)~(7)成立,则存在常数M1>0使得
(13)
证明首先,对参数γ>0定义辅助函数
g(s)=eγs2,∀s∈[0,M],
(14)
其中,M为定理1给定的。因此,可以得到
g′(s)=2γsg(s),
(15)
g″(s)=2γ(1+2γs2)g(s),
(16)
1≤g(s)≤eγM2。
(17)
利用模型(3)中的第1个和第3个方程,再结合式(15)(16),对∀t∈(0,Tmax)有


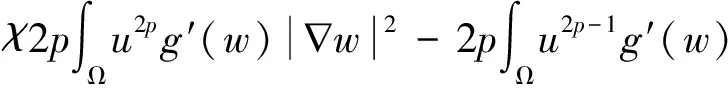
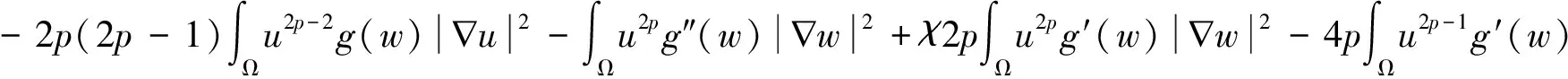

(18)
再由Young不等式可以得到
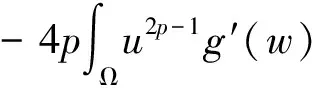
(19)

(20)
应用Gagliardo-Nirenberg不等式和Young不等式,结合式(7)(10)(15)(17),存在任意常数C3>0,有
(21)
其中,d1=eγM2(2γMr+2a1p+r),a=(np-(n/2))/(1+np-(n/2))。将式(19)~(21)代入式(18),结合式(10)(15)(16),有


(22)
对常数s∈R,令

因此,当f(s)=0时,h(s)至少存在1个正解,则可以找到γ>0满足
使得
由式(22)可以得到
再由式(17)和引理4可得式(13)。
引理7[11]假设定理1的条件成立,则存在常数M2>0和M3>0使得对∀t∈(0,Tmax),有
(23)
(24)
引理8假设定理1的条件成立,则存在常数M4>0使得对∀t∈(0,Tmax),有
(25)

(26)
接下来,由式(11)(23)和B(t)的定义,有
(27)
其中,θ=2(p-1)q/(2(p-1)-q)>1。令f(u)=a1u-a1b1uα,则存在任意常数C4>0使得
结合Neumann热半群光滑估计[12]可以得到对任意t∈(0,Tmax),存在任意常数C5,C6>0,使得
(28)
再由内插不等式可知,存在任意常数C7>0,对∀t∈(0,Tmax),有
(29)
其中,1/q=a+(1-a)/2p(a∈(0,1))。将式(27)~(29)代入式(26),则存在任意常数C8,C9>0使得对任意t∈(0,Tmax),有

引理9假设定理1的条件成立,则存在常数M5,M6>0,使得对∀t∈(0,Tmax),有
(30)
(31)
证明由模型(3)中的第1个方程可知



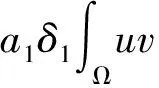
(32)
由文献[13],有
(33)
由文献[14]和式(25),有
(34)



(35)
对于I2(t),由文献[15]中的式(3.35)~(3.38),有
(36)
(37)
将式(35)~(37)代入式(32),可以得到
(38)
由Young不等式和式(34),有
再根据式(12),则式(38)可以写成
(39)
根据模型(3),令f(x,t)=-λ(u+v)w-μw+r(x,t),则w满足
因此,结合式(7)(10)(11)(25),存在任意常数C11>0使得对∀t∈(0,Tmax-τ),有
(40)
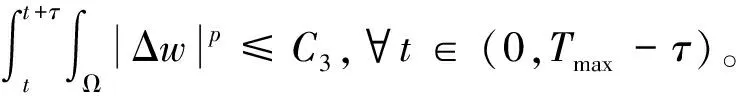
引理10假设定理1的条件成立,则存在常数M7>0,使得对任意t∈(0,Tmax),有
(41)
证明当p>1+(n/2)时,可以找到任意常数q满足n 后面的证明与引理8类似,因此可以得到引理10的证明。 引理11[7]假设定理1的条件成立,则存在常数M8>0使得对任意t∈(0,Tmax),有 (42) 引理12假设定理1的条件成立,则存在常数M9>0使得对任意t∈(0,Tmax),有 (43) 证明对模型(3)的第1个式子进行计算,有 此时,可以用类似于引理9的方法计算得到 由模型(3),可令f(x,t)=-ξ∇·(v∇u)+a2v(1-b2vβ-1-δ2u)满足 最后,根据引理2、引理8~12,再结合引理1,可以得到Tmax=∞和定理1的证明。 通过应用Lp估计、Young不等式、Hölder不等式、内插不等式、Gagliardo-Nirenberg不等式和Neumann热半群理论等,发现当初值和参数满足一定的正则性和限制条件时,可以得到在高维空间中模型(3)解的全局存在性和有界性。最终结果表明,通过提高空间维度,可使对模型(3)的研究更有难度,同时在生物学上更具有实用性。



3 结论

