不同时间尺度多源时序数据的FEEMD分解比较研究
王 正, 邱士可, 曾 群, 吕言利, 王 超, 张起萍, 李双权
(1.河南省科学院地理研究所, 郑州 450052; 2.河南省遥感与GIS重点实验室,郑州 450052;3.华中师范大学城市与环境科学学院, 武汉 430079; 4.北京国遥新天地信息技术股份有限公司, 北京 100083)
众多的海洋生态学和动力学研究表明,海表叶绿素a浓度的变化是浮游植物对多个物理环境因素微弱变动信号的非线性放大响应[1].因此,表征浮游植物丰度的海表叶绿素a浓度与多个环境因子间存在密切的内在关系[2-3].研究影响长时间序列海表叶绿素a浓度的环境因子[4]发现,太阳有效光合辐射(photosynthetically active radiation,PAR )和海面风场影响海洋上层环境;海表温度(sea surface temperature, SST)、海面高度(sea surface height, SSH)、海表盐度(sea surface salinity, SSS)、海表密度(sea surface density, SSD)、水体的分层结构(用混合层深度(mixed layer depth, MLD)来表示)表征海洋上层的热力和动力状况[5];基于海表风场的风速(wind speed)和风应力(wind stress)计算的风应力旋度和埃克曼抽吸速率参量,表征浮游植物生长的温度和营养盐供给,与叶绿素浓度关系密切[6-12].这些环境参量都是影响海表叶绿素a浓度的关键因子.
中国南海东北部海域受到黑潮、闽浙沿岸流、吕宋西北部上升流、内波、季风、河流输入等多个因素的影响,位置特殊,水文环境复杂,水体动态度较高,该区域的浮游植物和相关多个环境因子也呈现出高动态度特征.因此, 对该区域21 a(1998—2018年)的叶绿素a浓度及多个相关环境因子8 d和月尺度数据进行分解面临较多挑战,迫切需要一种适合该区域特征的数据分解方法,以分析叶绿素a浓度和多个环境因子蕴含的内在机制和规律.
目前,常见的时序数据分解方法有经验正交函数分解法(empirical orthogonal function,EOF),傅里叶变换, 小波变换等[13-14],然而,使用这些方法需要满足一定的前提条件[15-16].傅里叶变换需要假定信号按照固定的时间完全重复,EOF变换极度敏感于所选数据的时间与空间范围;而小波变换需要先确定基函数,再以基函数为基数对时间序列数据进行分解.海洋叶绿素浓度的变化是对海洋物理环境因子变化的非线性多尺度响应,多个环境因子数据量大、影响因子多样、变化比较剧烈,因此如果利用常用的方法进行时序数据分解具有一定的局限性,需要用非线性自适应的方法来进行数据分析.经验模特分解法(empirical mode decomposition, EMD)以及基于EMD发展的集合经验模态分解法(ensemble empirical mode decomposition, EEMD)、互补集合经验模态分解CEEMD(complementary ensemble empirical mode decomposition, CEEMD)等系列方法能将频率不同的不规则时间序列的信号按照不同频率进行分解[17],是一类自适应的数据处理方法,非常适合非线性、非平稳态和多尺度时间序列数据的处理,已在数据预测、信号分解领域得到推广, 尚未在遥感领域广泛应用[18-21].
因此,本文选用南海东北部区域1998—2018年共21 a的8 d和月尺度: SST、 海表面高度异常数据(sea level anomaly, SLA)、 SSS、MLD、 wind stress、wind speed、PAR、SSD这些物理要素与叶绿素a浓度数据进行FEEMD分解和比较,以分析和探讨其内在的机制关系.
1 数据及方法
1.1 研究区域
南海位于中国大陆的南方,是太平洋西部海域,夏半年5—9 月盛行西南季风, 台风频繁;冬半年盛行东北季风,季风稳定且强度很大.同时,南海既处于太平洋、印度洋和青藏高原的交互区域,又位于印度洋和太平洋两个沃克环流的交汇点上,还受黑潮入侵、闽浙沿岸流、珠江和湄公河等多条大河输入的影响.多尺度强迫影响下南海处于气候变化的敏感区域,各种尺度的海洋动力过程如中尺度涡旋和上升流频发.南海东北部海区(图1的NE区域)除了受南海多尺度多因素影响外,更位于太平洋和南海水体交换的主要通道,许多研究表明该区域常年有冷涡、上升流和大规模浮游植物叶绿素a浓度极值现象的发生[22-25].因此,本文在南海东北部海洋环境状况极端复杂的NE区域开展叶绿素a浓度和多个密切相关环境因子间的长时序数据分解研究.
1.2 研究数据及来源
本文使用的L3级8 d和月尺度合成叶绿素a浓度ChlOC5数据自Global Color免费获取 (表1), Global Color提供了4 km、9 km和25 km 的产品,包括 MERIS、MODIS、SeaWiFS 、VIIRS和OLCI以及这些多传感器合成的产品,数据空间覆盖范围为全球,时间范围从1997年9月1日—2023年7月(本文成稿时间).SST数据由美国国家气候数据中心(National Climatic Data Center,NCDC)提供,该数据是经过最优插值法插值的AVHRR4级的产品,时间分辨率为每天,空间分辨率为0.25度,数据的时间尺度跨度自1981年9月至今.法国AVISO数据中心提供了融合多源卫星测高数据的SSH和海面高度异常数据(sea surface anomaly, SLA),该数据是TOPEX/Poseidon、ERS-1/2、ENVISAT Jason-1和Geosat Follow-On这4种测高卫星经交叉定标的网格化海平面高度融合数据.ASCAT风场数据为插值后的8 d和月尺度的全球风场数据,空间分辨率为0.25度×0.25度,参数包括海表面的wind speed和 wind stress.MLD数据是基于阈值法计算的, 使用了周和月尺度混合层再处理数据, 这两种再处理数据的空间分辨率为25 km, 数据共有33层,本文所用的表层数据是从1998年1月1日到2018年12月31日的周和月尺度数据.SSD数据通过微波遥感技术间接反演获得,再结合实测的数据和数值模拟数据同化而来的,SSD数据与SSS数据都下载自法国CMEMS. PAR数据下载自欧空局的Global Color计划所提供的长时间序列的多传感器融合数据,参数包括了生地化参数,海洋表层光学参数、大气参数和表观光学参数;本文使用的是从1998年到2018全年8 d和月尺度时间分辨率的融合数据.本研究所用数据及下载地址见表1.

表1 本文所用数据及下载地址(1998-01—2018-12)
1.3 EMD、 EEMD FEEMD数据分解法
经验模态分解方法是一种具有良好自适应数据处理能力的方法,非常适合非线性、多尺度非平稳态的长时间序列数据的处理,该方法的本质是对数据序列代表的信号进行平稳化处理[26].其基本思想是将时间序列数据信号看作是频率不同的不规则波, 并按不规则波的不同频率将时序数据分解为多个单一频率的波和剩余残波的形式.其基本步骤为:
1) 求取时间序列信号x(t)的极值点,包括极小值点和极大值点;
2) 利用三次样条函数构造时间序列数据极大值点和极小值点的上下包络线,并计算其均值函数m1;
3) 验证h1=x(t)-m1是否符合本征模态函数(intrinsic mode function, IMF)的条件,如符合则进行下一步计算,如不符合则重复步骤1和步骤2,直至符合条件为止,结果即为第一个IMF,imf1=h1k;
4) 得到原始时间序列数据扣除第一个IMF后的第一个残留r1=x(t)-imf1.重复以上步骤,则可得到从高频到低频的各模态IMF;
5) 原始时间序列数据信号扣除各IMF,直至剩余的信号最后变为单调信号Res(趋势),即只存在一个极值点的情况为止.则原始时间序列的信号可表示为:
(1)
其中,每个本征模态都必须满足数据序列中极值点的个数与过零点的数目相等或相差不超过一个点, 并且时序数据中由局部最小值和局部极大值所构成的上下包络线的均值为零[26].
然而,虽然EMD方法适用于非线性、非稳定态时间序列数据的分析,但在实际时序数据处理中由于原始信号极值点不均匀分布和极值突变会使得数据丢失一部分的时间或频率尺度,导致模态混叠问题.模态混叠是指相近的特征时间尺度分布在不同的IMF中, 或者单个IMF包含差异极大的特征时间尺度, 导致相邻的2个IMF相互影响造成波形混叠难以辨认.当混叠模态出现时,分解的本征模函数(IMF)是没有实际物理意义的.为了解决模态混叠的问题,吴召华教授等在EMD的基础上,发展出了集合经验模态分解法[27].其基本思想是:将频率平均分布的高斯白噪声加入到时间序列数据中,并将其看作是信号,则信号具有了在不同尺度上的连续性,可以减小在EMD中存在的模态混叠现象.EEMD分解的步骤与EMD分解的步骤类似:
1) 将均值为0,频谱正态均匀分布的高斯白噪声ni(t)多次加入到初始序列数据信号s(t)中,加入的白噪声的标准差为原始信号标准差的0.1~0.4倍,即
xi(t)=s(t)+ni(t),
(2)
xi(t)为第i次加入的白噪声的信号;
2) 对序列数据信号xi(t)进行集合经验模态分解,即可得到分解后的各模态分量imfij和趋势项res;
3) 通过n次重复步骤1)和2)对相应的各IMF分量取均值,以消除高斯白噪声对序列数据信号的影响,结果得到的IMF为
(3)
若重复次数越多则n越大,则对应的白噪声的各个IMF和越趋近于0.因此,可将EEMD分解的结果展示为:
(4)
EEMD通过加入高斯白噪声的方式,消除EMD中的模态混叠现象,比EMD的分解更科学准确.然而,EEMD中也存在残余辅助噪声的影响(图2c).Yeh等通过将随机高斯白噪声以正负成对的方式加入到时序信号中,发展出了互补集合经验模态分解方法(complementary ensemble empirical mode decomposition, CEEMD)[28],CEEMD就是FEEMD的核心算法.实验结果表明,FEEMD能有效消除时序数据信号中残余的辅助噪声,不仅保留了EEMD在处理非平稳信号方面的优点,又完善了EMD的模态混叠问题,且计算结果表明FEEMD的去噪和抗干扰能力优于EMD和EEMD(图2d).CEEMD分解的步骤为:

图2 基于8 d尺度数据的EMD、EEMD和FEEMD分解结果的对比
1) 将n组正负成对的辅助白噪声加入到原始数据序列信号中.白噪声的取值范围为0.1~0.4,即白噪声的标准差为原始信号的0.1~0.4倍.则可获得一个包含2n个数据序列信号的集合:
(5)
其中,加入正负成对白噪声后的时序数据信号为M1和M2,S是原始的时序数据信号,N为加入的辅助白噪声;
2) 按照EMD分解的步骤依次对数据集合中的每个时序数据信号分解,则每个信号可得一组IMF分量,因此,imfij即为第i个分量和第j个本征模态函数的分量;
3)imfj即为多组分量取均值后得到的分解后结果:
(6)
其中,imfj为FEEMD分解后获得的第j个IMF分量.FEEMD分解后,产生的各个imfj根据频率由高到低依次排列,高频和低频噪声分别出现在靠前和靠后的几个模态分量中,通过显著模态检验可判断分解出的是噪声还是具有实际物理意义的信号,分解至最后剩余的信号即为该时序数据的总体变化趋势.
2 结果
2.1 三种数据分解方法的比较
为比较EMD、EEMD和FEEMD的数据分解方法结果,基于南海北部NE区域8 d合成的21 a时间序列叶绿素a浓度数据进行分解.图2即为对该时间序列数据(图2a)进行EMD分解(图2b)、EEMD分解(图2c)、FEEMD分解(图2d)的结果.其中,由于21 a的8 d尺度数据共有966期,则可分解出10个模态变量,其中第1个变量为加噪声的原始信号,第2~8个分量表示的是从高频到低频的各个模态的变量,第9个模态表示的是整个周期时间序列详细的变化过程,第10个分量表示21 a总体的变化趋势.
图2中的b、c、d都能反映出数据的总体趋势(R),且三者分解出趋势是一致的,在低频的第9模态(C9)和第10模态(R),三者是相似的.然而, 图2b和2c都存在不同程度的模态混叠现象,该现象在C2和C3高频模态中尤为明显.其中,C2和C3模态的波形高度相似,此外在EMD分解的结果中(图2b),模态C4和模态C5在同一模态中出现了其他模态才出现的频率,这种现象在EEMD分解的结果中有所改善(图2c).FEEMD的结果(图2d)则避免了这些问题,同时FEEMD分解的运行效率相较于EMD和EEMD提升了10倍以上.因此,本研究选用FEEMD来进行数据分解和后续处理是合理的.
2.2 研究区域的时序数据的FEEMD分解
研究表明南海东北部区域(NE区域)的叶绿素a浓度存在显著的周期性和季节性[3].为了对比不同时间尺度数据的分解结果,本文对比分析了NE区域月尺度数据(NE-monthly)来与8 d尺度数据(NE-8d)的分解结果.此外,为了分析影响NE区域显著周期性现象的关键因子,本文对影响海洋叶绿素a浓度的环境因子SST、SSH、MLD、PAR、SSS、SSD、 wind stress和wind speed的8 d和月尺度数据也进行了FEEMD分解.需注意的是,分解出的模态个数由数据的长度来确定,数据长度越长,则分解模态数目越多,可以通过log2n来确定模态数,其中的n为数据的长度.因此,8 d尺度21 a共966期数据可以分解出10个模态,月尺度21 a共有252期数据,则可分解为8个模态.
FEEMD对8 d尺度数据加0.4的噪声,集合训练200次;共分解出10个模态,其中第1个模态(C1)为加噪声的原始信号,模态的性质与噪声类似,故各变量的第一模态(C1)不参与讨论.第9个模态表示的是整个周期时间序列详细变化过程,第10个模态表示21 a总体变化趋势,因此在显著性检验时,仅检验C2~C8这7个模态(图4).本文分解并展示了NE-8 d(图3)和NE-monthly(图4)的结果.各环境因子C1模态的性质与噪声类似,因此8 d和月尺度的各变量的C1模态均不参与讨论.
2.3 FEEMD数据分解结果的显著性检验
使用IMF平均周期与能量关系分布特征显著性检验来判别FEEMD分解出的各IMF是噪声还是具有实际物理意义的量.如果分解出的各个模态的结果是在95%的置信线以上,则为具有真实物理意义的参量,在95%的置信线以下,则认为是噪声.
图5为NE-8d的FEEMD分解出的各个模态的显著性检验结果,图5中除了ChlOC5的C8模态和PAR的C6模态未通过显著性检验外,其它各参数的各模态均通过显著性检验,为具有实际物理意义的信号.图6 NE-monthly为基于月尺度数据分解出的各个模态的显著性检验的结果,SST、MLD、PAR、SSD和wind speed为仅C2模态通过显著性检验的参量;ChlOC5和wind stress为C2和
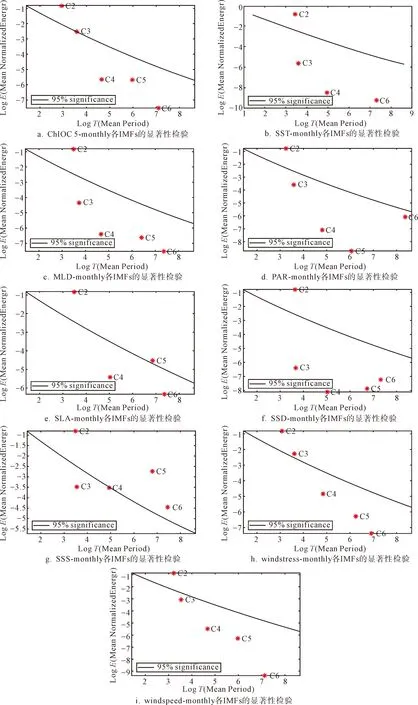
图6 NE-Monthly FEEMD分解的各个模态的显著性检验
C3模态通过显著性检验的参量; SLA为C2和C5模态显著的参量, SSS为C2、C4、C5和C6通过显著性检验的参量.通过对比8 d尺度和月尺度数据FEEMD分解结果的显著性检验可知,8 d尺度数据分解出比月尺度更丰富的、具有实际物理意义的显著模态.
3 不同时间尺度数据的趋势、周期对比及分析
已有的长时序数据时空变化研究中,常用月尺度数据进行分析[29-31].8 d尺度数据相较于月尺度数据,有何异同, 能否发现月尺度数据未能发现的现象或规律,是本节也是本文关注的问题之一.
3.1 NE区域8 d与月尺度总体趋势的比较
图7和图8分别为8 d和月尺度叶绿素a浓度与相关环境因子数据在NE区域21 a的变化趋
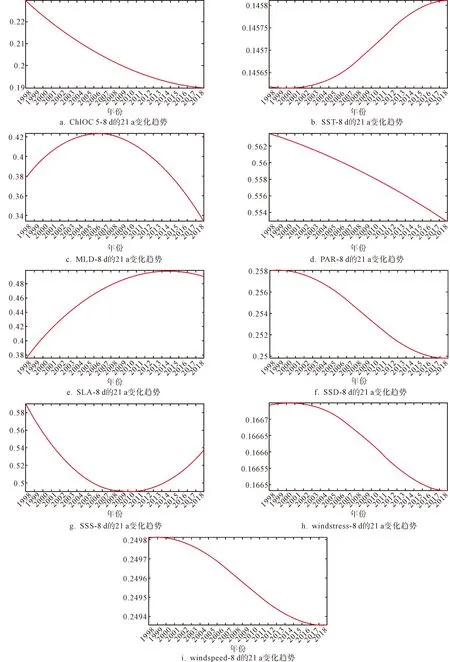
图7 基于8 d尺度数据分解出的NE区域各个因子21 a总体趋势
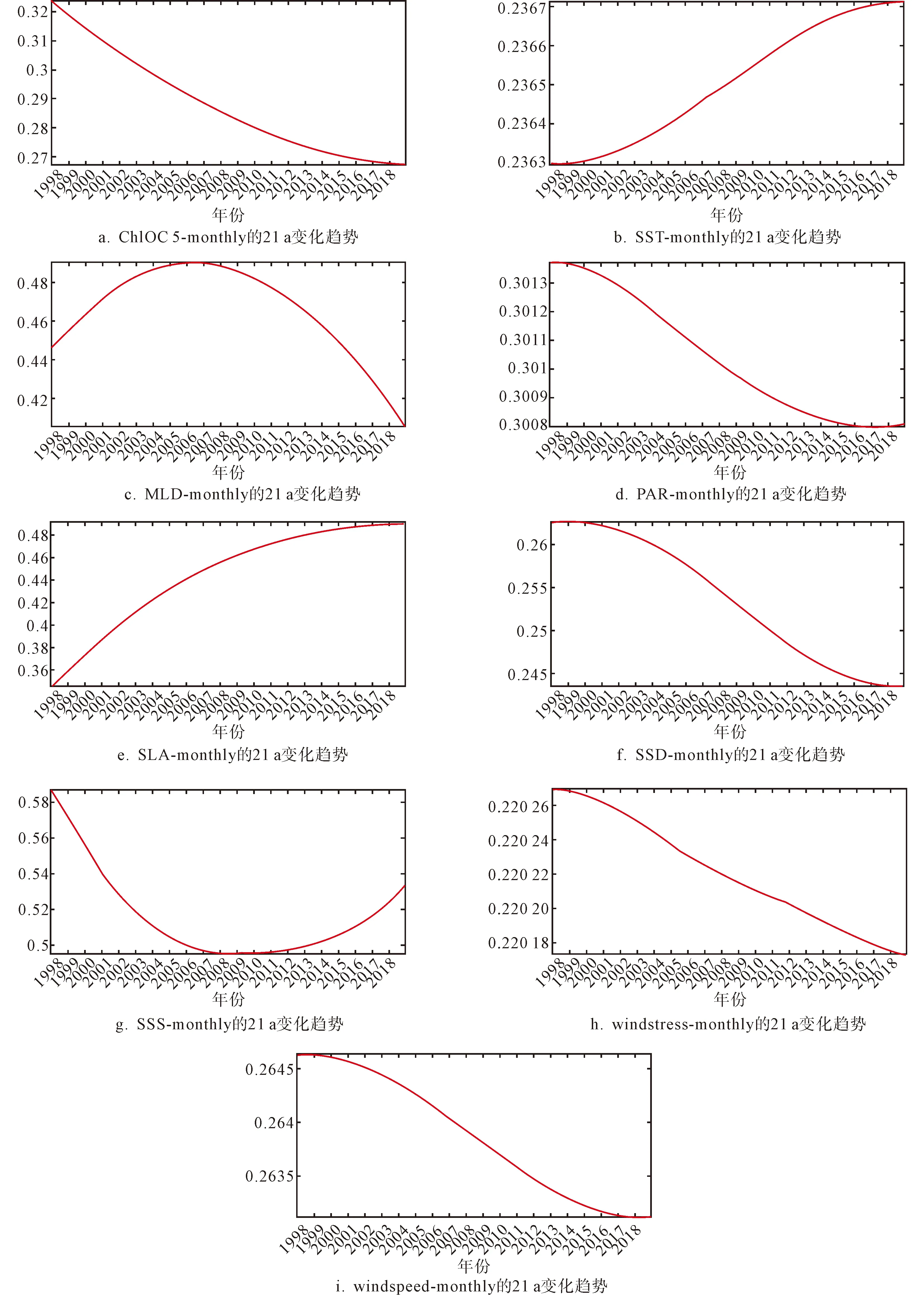
图8 基于月尺度数据分解出的21 aNE区域的总体趋势
势.从图7可知在NE区域21 a的叶绿素a浓度的总体趋势是下降的,与之对应的SST呈上升趋势,MLD呈先上升后下降的趋势,NE区域的PAR也呈现下降趋势,SLA呈先上升后略有下降的趋势,SSD呈下降趋势,SSS在1998-2010年呈现下降趋势,2010-2018年呈现上升趋势,21 a的wind stress, wind speed 也呈下降的趋势.对比8 d(图7)和月尺度(图8)数据的变化趋势,发现两者趋势一致,表明FEEMD方法具有较好稳定性.
3.2 月尺度与8 d尺度数据分解出的周期对比
为进一步比较8 d尺度与月尺度数据的FEEMD分解结果,利用经过显著性检验的模态来计算显著模态周期和方差贡献.计算周期的方法主要有两种,基于瞬时频率和基于零点数的方案.在利用瞬时频率方案计算平均周期时,容易出现异常值.研究结果显示,出现异常值是因为出现了负的瞬时频率,零点数方案则可以有效的避免此种情况的发生,因此采用零点数方案来计算显著模态的平均周期.
图9a为8 d尺度的叶绿素a浓度数据分解出的显著模态平均周期,C7模态为平均63个月的周期,C6模态为31.5个月的周期,C4和C5模态为准年周期,C3为季节周期/半年周期,C2为月尺度周期.综合图9中的所有因子可知,基于8 d尺度的数据可分解出准年周期的模态(C4模态),也可分解出年际(C5/C6模态)和年代际周期的模态(C8/C7模态),值得注意的是,基于8 d尺度的数据可以分解出季节尺度(C3模态)甚至是月尺度(C2模态)的周期.图10为各因子显著模态的方差贡献,由图10 (a~i)可知,第四模态的方差贡献最大,对于ChlOC5因子C2~C4模态累计贡献了所有模态的总方差的83.4%左右(图10a),SST的C2~C4模态累积贡献了总方差的97%左右(图10b),MLD的C2~C4模态累计贡献了总方差的89.2%左右(图10c), PAR的C2~C4模态累计贡献了总方差的95.6%左右(图10d); SLA (图10e), SSD (图10f), SSS (图10g), wind stress (图10h) 和wind speed (图10i)这些因子的C2~C4模态累计的方差贡献分别为79%,96%,63%,85%,92.5%左右.
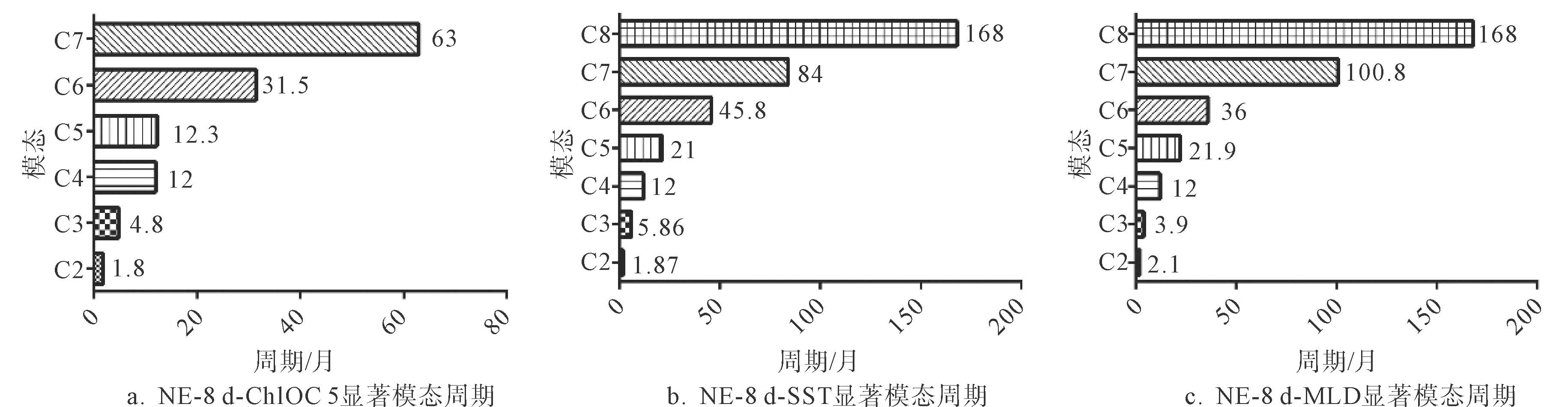
图9 区域NE-8 d各环境因子的显著模态的周期
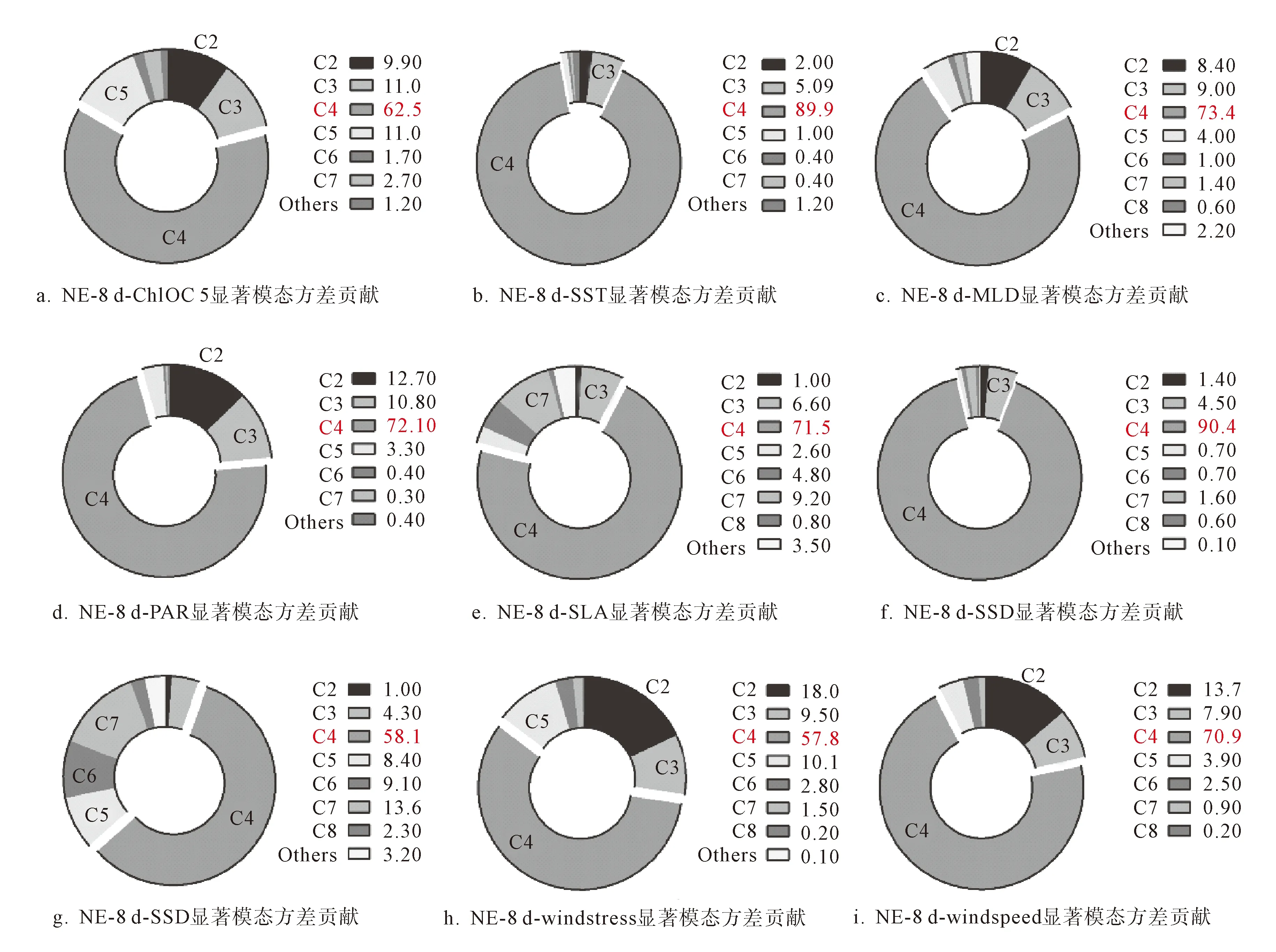
图10 区域NE-8 d尺度各环境因子显著模态的方差贡献/%
综合图9和图10来看,各个模态中,方差贡献最大的是C4模态,C4模态主要体现的是年尺度的变化趋势,C4模态的方差贡献在57%以上,最高可达90%左右.值得注意的是,除了方差贡献最大的C4模态,方差贡献第二和第三的模态周期一般为C3和C2模态的周期(图10),个别的因子除外.C3和C2模态分别对应于季节周期和月尺度的周期.图9所有因子的C2模态反映的周期从1.8~2.1个月不等,但主要是1.8个月左右的短时间频率的周期,图9的C3模态反映的是从3.7~5.86个月的季节尺度和半年尺度的周期.
表2是NE区域基于月尺度的各个因子的数据,在FEEMD分解后,经过显著性检验的模态所计算的平均周期,方差贡献和累积方差表.可以看出,NE区域的月尺度数据FEEMD分解结果的能量分布主要集中在C2模态上,NE区域的ChlOC5-monthly的C2模态方差贡献达到70.5%,显著的C2和C3模态的方差贡献达到了93%,ChlOC5-monthly主要为年尺度周期.此外,SST-monthly,MLD-monthly, PAR-monthly, SSD-monthly, wind speed-monthly通过显著性检验的模态为C2,周期分别为12、12、11.7、12.3、11.5个月,C2模态的方差贡献分别为94.7%、86%、86.4、95.2%、78.4%.除了这些环境因子外,还有其他环境因子有两个及以上模态通过显著性检验,SLA-monthly的C2和C5模态通过了显著性检验,C2模态反映了显著的年周期变化情况,C5模态反映了显著的168个月的年代际的变化情况,C2模态的方差贡献为81.6%,C2和C5模态累积的方差贡献为87.9% .SSS-Monthly的显著模态有C2、C4、C5和C6模态,周期分别为12.3、45.8、100.8和168个月,显著模态的方差贡献最大的是C2模态,为58.2%,几个显著模态累积的方差贡献为87.3%.wind stress-monthly的显著模态C2和C3的周期可看作准年周期,累计方差贡献达到92.1%.NE-monthly的ChlOC5和各环境因子分解结果可以反映出该区域显著的年周期变化情况以及年际的变化情况.
综合来看,NE区域的8 d和月尺度数据的FEEMD分解结果都可将该区域最显著的年尺度周期信息表征出来,此外两者都分解出年际和年代际的周期.然而两者又有不同,8 d尺度数据的结果,可分解出显著的半年尺度的变化周期、季节变化的周期和月尺度变化周期,这是月尺度的数据所无法做到的.另外,基于FEEMD分解的8 d尺度数据能分解出从短到长的不同周期,而月数据的FEEMD分解结果主要以准年周期为主.
4 讨论
本文利用FEEMD方法分解了月尺度和8 d尺度数据,通过比较分析两者具有实际物理意义的显著模态、模态周期、模态方差贡献等发现,8 d尺度数据可分解出较多的显著模态,较详细的不同时间长度的周期(既有年代际、多年周期,也有年际和年周期,更有半年周期、季节周期和1.8个月周期);与之对比明显的是基于月尺度数据分解的周期主要是年周期,8 d尺度数据可以发现月尺度数据发现不了的周期和规律.研究发现FEEMD在复杂环境下具有较强的数据分解能力.
NE区域处于气候变化的敏感区,该区域叶绿素a浓度表征的浮游植物和相关环境因子共同处于海洋和大气动力学过程影响之下,受到多尺度因素和物理过程的影响,使得该区域的叶绿素a浓度和相关环境因子具有显著的年内、年际、代际特征和趋势.将不同时间尺度的叶绿素a浓度及环境因子信号正确地归因,有助于了解不同季节、ENSO、年代际、长期变化背景下各因子的特征、影响及相互联系.利用FEEMD方法能成功的将多尺度信息从干扰较多的混合信息中分解出来,较适用于复杂环境下的数据分解,能为研究不同尺度各因子之间的驱动关系提供借鉴.

