基于公交数据挖掘的乘客上下站点识别
张杰 唐耀红 袁秋凤 王伟






摘 要:为制定符合客流的线路公交调度方案,增大公交出行吸引力,减少私家车出行碳排放,有必要提出精确的线路乘客上、下车站点识别方法,获取精确客流数据,为公交调度提供精细数据支撑。本文以福州市常规公交多源数据为基础,针对数据缺陷提出系统时间误差修正及站间缺失数据修复的数据预处理方法。在此基础上,提出乘客刷卡时间与公交到离站时间匹配的上车站点识别方法。将乘客出行行为按照是否具有出行规律,提出基于乘客出行规律的乘客下车站点识别方法及综合出行距离、换乘能力、出行吸引强度、周围土地利用性质等因素影响下的乘客站点下车概率识别方法。最后,以福州市125路公交数据为例,将识别数据与实际调查数据对比,验证识别方法的准确性。研究结果可为城市公交客流OD调查提供数据挖掘方法,减少传统调查产生的人力物力,以及为公交企业运营调度提供数据支撑。
关键词:城市交通;站点识别;出行规律;数据挖掘
中图分类号:U121
文献标志码:A
公交乘客上下站点的客流是优化公交调度,提高公交吸引力,进而减少私家车碳排放的基础。近年来,随着移动端支付的发展,通过数据挖掘获取的乘客上下站点数据比以往人工调查更为精确省时,但国内现有公交系统,大多采用“一票制”的收费方式,无法直接获得乘客的下车站点,并且公交数据多存储在不同的系统当中,直接获取乘客的上车站点存在精度不够高的问题。因此,有必要研究更为精确的乘客上下车站点的匹配方法,为公交调度提供精细化的数据基础。
LEE等[1]通过首尔市公交IC卡数据及地图API服务,识别各个站点的上车人数。EGU等[2]采用相似度度量结合聚类算法,对具有出行行为相似的客流进行识别。TANG等[3]结合天气因素,采用梯度提升决策树法对乘客下车站点进行预测。CHEN等[4]建立了在站点数据缺失情况下的聚类模型,用于乘客上车站点的识别。HUANG等[5]通过密度聚类算法和时间校正策略生成公交到站时间,用于匹配乘客刷卡数据,进行上车站点识别。谢振东等[6]以线路平均站间距离与平均行程时间为变量求得刷卡时间阈值,通过最短时间聚类法对乘客的上车站点进行识别。邬群勇等[7]按照工作日和不同出行目的对上车乘客进行聚类,并提出不同时空状态下的客流热点站点。秦政[8]通过历史调查统计,提出了基于威布尔分布的乘客下车概率模型。左快乐[9]基于OD反推矩阵对乘客下车站点进行推算。张文胜等[10]引入时间弹性准则,结果表明在时间弹性准则下识别出的上车人数要大于聚类分析得到的上车人数。孙凯等[11]通过结合乘客出行站点数量规律,改进站点吸引强度方法对乘客下车站点进行识别。
国内外对于乘客上下车站点匹配的研究成果丰富,多从数据挖掘入手,利用各类聚类方法展开研究,而在数据误差及从乘客出行规律方面对乘客上下车站点的研究较少。因此,本文以福州市多源公交数据挖掘为基础,根据多源数据上传特点修复数据误差,提高数据匹配精度;在此基础上,分析乘客刷卡数据的出行规律,以期提出匹配率更高的乘客上下车站点匹配方法。
1 公交多源数据预处理
本文所涉及公交多源数据包含3个方面:乘客通过各种支付途径产生的的公交刷卡数据,公交GPS数据,线路信息、站点信息、调度信息、车辆信息等其他公交数据。
1.1 修正系统时间误差
部分城市公交刷卡系统没有记录乘客刷卡数据上传站点经纬度数据,无法直接识别上车站点,需要结合公交GPS运营数据、通过时间匹配补充站点信息。由于数据存储在不同的系统中,导致公交刷卡数据采集系统与公交GPS运营系统的上传时间存在误差。如图1所示,当公交刷卡数据上传时间早于公交GPS时间或晚于公交GPS时间时,二者时间匹配会导致部分刷卡乘客被判定为无效数据,导致匹配结果与实际情况误差增大。因此,要对两个系统间的时间误差进行修正。
以公交车辆GPS系统时间作为参照,假设二者间的误差为Δt,则
Δt=TS-TGPS(1)
式中:TS为乘客刷卡数据上传时间;TGPS为公交GPS到离站数据上传时间。
因此,经过误差时间修正后的乘客刷卡数据上传时间T′S可以表示成
T′S=TGPS=TS-Δt(2)
1.2 修复站间缺失数据
当班次存在站间数据缺失时,会导致缺失站点上车乘客其刷卡数据无法匹配,需要对缺失站间数据进行修复,本文仅需对公交站点缺失的到站时间进行修复,即可完成多源数据的时间匹配。因此,本文采用最大概率模型对缺失站点数据修复。
1)站间数据修复模型及参数
一方面,当缺失站点存在乘客乘车刷卡时,通过乘客刷卡数据时间与公交GPS到站时间的关系,对公交车辆到站时间进行数据修复;另一方面,当缺失站点不存在乘客乘车,通过该缺失站点历史到站数据,以及该站点历史到离站数据中完整的到离站数据建立上一站点到该站点的行程时间合集,构建数学概率分布模型,对缺失数据进行修复。
假设集合Ux={Xf1,Xd1,Xd2,Xd3,…,Xdn,Xf2}为某线路某一运营班次行驶过程中连续经过的站点,其中,Xf1、Xf2为到离站数据完整的站点,Xd1、Xd2、Xd3等为到离站数据缺失的站点。
假设在数据缺失站点Xd1至Xdn途中,有乘客上车刷卡产生时间序列为TS=ts1,ts2,…,tsn,因仅在公交车到站后才存在刷卡行为,此时把各个数据缺失站点首条刷卡记录时间作为对应数据缺失站点乘客开始刷卡上车的时间。
设乘客所匹配的上车站点是Xdn,公交车到达该站点时乘客上车产生的刷卡上传时间依次表示为tks=tks1,tks2,…,tksn,其中sn为站点Xdn的上车人数。当数据缺失站点存在乘客刷卡数据可以匹配时,Xdn到站时间的推断即公交车从参照站点Xf1离站行驶至tks1的行程時间内,抵达Xdn概率最大的时间节点。
设任意两站点Xa、Xb间行程时间分布用概率分布Pa,b(t|θ)来表示。已知Xf1、tks1,借助历史公交GPS到离站数据,推断最佳Xdn到站时间的过程即以下极大值的推断过程:
X^dn=arg maxXdnPXf1,Xdn(t|θ,t=tks1)(3)
式中:X^dn为车辆从Xf1离站至tks1行程时间内,PXf1,Xdn(t|θ)取极大值时对应的到站时间;θ为后验条件参数集合。
当数据缺失站点不存在乘客刷卡数据时,根据历史车辆到离站数据,采用车辆从参照站点Xf1出站到Xdn的行程时间TXf1,Xdn进行推断,可表示为
T^Xf1,Xdn=arg maxTXf1,XdnPXf1,Xdn(t|θ)(4)
对于公式(3)、(4),应用以下后验条件:
(1)θ1=。此时PXf1,Xdn(t)为从Xf1至Xdn的历史行程时间概率分布;
(2)θ2=tf1±Δt。其中,tf1为站点Xf1的离站时间点,ΔT为行程时间阈值,PXf1,Xdn(t|tf1±ΔT)表示时刻tf1±ΔT时,从参照站点Xf1至数据缺失站点Xdn行程时间的条件概率分布,根据福州市站点布设距离,本文设定ΔT=600 s;
(3)θ3=ttra±30 s,其中ttra为车辆从参照站点Xf1出站到tks1的行程时间,PXf1,Xdn(t|ttra±30)表示行程时间为ttra±30 s时,从参照站点Xf1至数据缺失站点Xdn行程时间的条件概率分布。
从Xf1到Xdn符合条件(1)到条件(3)的行程时间合集通过该线路运营车辆历史公交GPS到离站数据获得。对于行程时间集合,为减小模型计算量,采用高斯分布函数拟合。
P(t)=12πδexp(-(t-μ)22δ2)(5)
2)模型总体流程
Step1 选取某一线路,将该线路运营班次按照时间顺序排序,对所有车次的车辆到离站数据按站点顺序进行整理;
Step2 将每一班次的到离站站点数与该线路的站点列表进行比较,若不存在站间到离站数据缺失,无需修复;
Step3 若存在站间到离站数据缺失,确定存在数据缺失的区间,以其前一个数据完整的站点作为参照点,从历史数据中获取参照点到缺失站点的行程时间,建立行程时间分布模型;
Step4 若该区间有乘客刷卡记录,将刷卡记录以时间排序,以第1个刷卡乘客的刷卡时间为准,根据步骤3的方法判断车辆从参照点离站时间至缺失站点第1位乘客刷卡时间为行程时间内概率最大的到达时间作为修复时间并记录;
Step5 若该区间内没有乘客刷卡记录,对数据缺失站点构建以参照站点到该缺失站点行程时间为条件的行程时间概率分布模型,求解模型概率极大值的时间值,作为车辆从参考点至该缺失站点的行程时间。
2 基于公交多源数据的乘客上下车站点识别方法
2.1 上车站点识别方法
乘客上车站点的识别原理如图2所示,在完成数据预处理后,结合车辆编号与发车时刻表等数据进行识别,其步骤如下:
Step1 根据线路号筛选出所需研究线路的多源数据,按时间进行排列。
Step2 提取排序在最前的运营班次信息,并筛选出对应时间节点的公交刷卡数据及该班次的各站点到离站时间。
Step3 设TS为乘客刷卡数据上传时间,TA为公交车辆到达站点时间,TV为车辆到达相邻下一站点时间,当前班次总的刷卡数据条数为N,N={1,2,…,N},所选取线路的站点总数量为I,I={1,2,…,I},则刷卡数据对应的刷卡站点为Sun,在站點i上车的乘客表示为Sui,当TAi<Tn<TVi时,认为该乘客Sui位于该站点Sun。
Step4 当一个班次的所有站点均遍历完成时,结束计算,统计各刷卡数据的匹配结果并记录,跳转至Step2继续下一班次的计算,直至所有班次的数据计算完毕。
2.2 基于出行规律的乘客下车站点识别方法
2.2.1 乘客公交出行规律分析
在工作日,选择公交出行的乘客往往具有一定的出行规律。例如,选择公交出行前往校园、工作地、市场的学生、工作人员、老人,在返程时多数时候也会选择乘坐公交车辆返回,将这类人群全天公交出行轨迹相连接,会形成一个闭合的出行链式形态,如图3。部分乘客在乘坐公交后,选择其他方式出行,将这类人群全天公交出行轨迹相连,则无法形成闭合的链式形态,如图4所示。
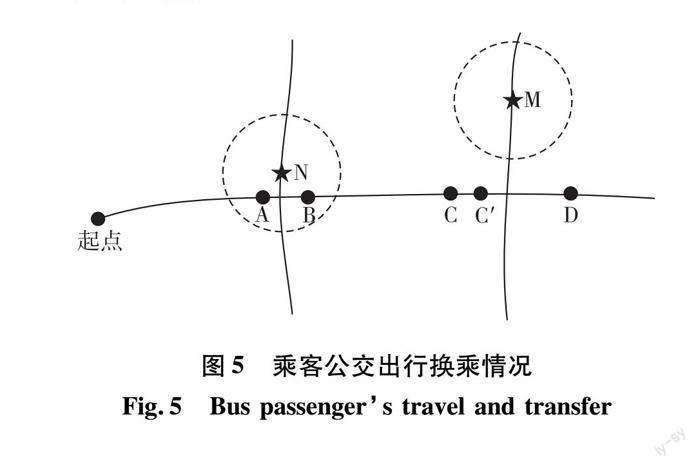
当一位乘客具备乘车出行规律时,可通过该乘客多次出行数据,判断其在所研究线路班次的下车站点。如图5所示,乘客乘坐某线路从起点出发,A、B、C、D为该线路的后续站点,C′为与C相对应的该线路返程站点,N、M为其他线路的站前往下一目的地点。
1)当乘客的第2次公交出行刷卡上车站点为A站点,推测这名乘客是在同一个站点进行换乘的。
2)当乘客的第2次公交出行刷卡上车站点为N站点时,该乘客的出行行为属于异站换乘,许多学者[12-13]研究将换乘距离的阈值设置为500 m。综合福州市公交站点覆盖率,本文将换乘距离的阈值设置为500 m,当站点间距为500米范围内时,将乘客的出行行为定义为异站换乘,当站点间距大于500 m时,认为乘客的出行属于图3~4的断开出行链现象。
3)当乘客的第2次公交出行在C′站上车时,由于C′为与C相对应的返程站点,且乘客在公交线路选择时有较强的往返规律,故将乘客这种出行行为定义为往返式公交出行,选择C′站点所对应的C站点为乘客前一次乘车的下车站点。
根据上述分析,定义连续公交出行为乘客当日前后两次乘车的空间间隔满足500 m换乘距离内时的公交出行,如图6。定义往返出行为乘客前后两次出行的乘车点为该次出行目的的起终点,如图7。
2.2.2 基于出行规律的乘客下车站点识别方法假设
假设条件1:根据连续公交出行规律,乘客相邻两次乘车记录中,前一回乘车的下车站点是后一回乘车上车站点或位于其换乘距离阈值内最近的站点;
假设条件2:根据往返出行规律,乘客一日内第1回出行的上车站点为乘客末回出行的下车站点或位于其下车站点在换乘距离阈值内最近的站点;
假设条件3:根据往返出行规律,乘客前后两回出行选择同一条线路,并且上下行相反,则两次乘车站点互为上下站点;
假设条件4:考虑到有出行规律的乘客存在偶然出行行为,因此,当乘客不具备出行规律时,提取乘客本周其他工作日刷卡数据进行识别,当有不少于2个工作日乘车记录中存在与研究日乘坐相同线路、运行方向、站点的乘车记录,其下车站点均能采用出行规律假设进行识别并且识别得出的下车站点一致时,判定其本次乘车的下车站点与符合条件的往日下车站点一致。
2.2.3 基于出行规律的乘客下车站点识别方法
以乘客在公交站点X选择q线路下行方向的车辆乘坐的出行进行说明,定义以下集合:
集合U1={x+1,x+2,…,n}表示乘客在公交X站点选择乘坐q线路下行方向的车辆,q线路所有站点中位于X站点之后的其他站点集合;
将集合U2定义为集合U1内站点500 m范围内的周边公交站点集合。
设乘客在本次公交出行后,下一回公交出行的上车站点为O,求解乘客在q线路后续站点y的下车概率,可得:
1)若站点O∈U1,说明乘客后一回乘车的站点处在X站点的后续站点集合内,这符合乘客公交出行的连续公交出行规律,在站点y的下车概率为
Py=1,O=y0,O≠y (6)
2)若站点O∈U2,说明乘客后一回乘车的站点处在X站点的后续各个站点的500 m范围内其他可乘坐站点集合内,设距离y站点附近的站点为y′。由前文分析可知,乘客在该集合内的站点上车符合乘客公交出行的连续公交出行规律。在站点y的下车概率为
Py=1,O=y′0,O≠y′ (7)
3)若站点O不在集合U1和U2中时,根据假设条件4,提取乘客该周工作日除研究日外其余天数内存在乘客选择q路公交在站点X乘坐同一方向车辆的乘车记录,当日乘客在本次乘坐公交后相邻下一次乘坐公交的上车站点O′属于集合U1或集合U2并且下车站点一致,当符合这种情况的其余工作日天数不少于2 d时,判定本次乘车的下车站点与符合条件的往日下车站点一致,在站点y的下车概率为
Py=1,O′=y或y′0,O′≠y或y′ (8)
2.3 基于站点下车概率的乘客下车站点识别方法
对于偶然出行、单程出行等情况的乘客,出行目的决定了这次出行的下车站点,当站点包含更多吸引乘客下车因素时,乘客在这个站点下车概率越大。因此,从各个站点下车概率角度,对乘客下车站点识别进行补充。
用一趟公交运行班次对计算方法进行说明。设研究线路一趟公交途经I个站点,各个站点i上车人数为Ai(i=1,2,…,I)。设Pab是出行人员位于a站上车到b站下车的概率(a=1,2,…,I-1;b=2,3,…,I;且a<b)。设Di是出行人员位于第i站的下车人数。
在首站,无人下车:
D1=0(9)
当车辆行驶至第2站停车,在首站上车人员有一定概率会在本站下车:
D2=A1×P12(10)
以此类推,当车辆行驶到末站停车,表达式为
DI=A1×P1I+A2×P2I+…+AI-1×PI-1I(11)
综上,针对随机站点i,Di可以表示成
Di=∑i-1a=1(Aa×Pai)(12)
假设选择乘坐公交的乘客位于任意a站点乘车前往b站点的概率是Pab,其受到出行距离影响的下车概率是Qab、受到b站点换乘能力吸引的下车概率是Fb、受到b站点出行强度吸引的下车概率是Wb、受到b站点土地利用性质吸引的下车概率是Rb,这些因素综合影响乘客在b站点的下车概率,Pab可表示为
Pab=Qab×Fb×Wb×Rb∑nk=1+aQak×Fk×Wk×Rk(13)
将Pab归一化,代入未匹配上车乘客数,可计算每站下车人数。
1)出行距离影响
有学者[14]研究得出乘坐公交出行的人群在出行距离上近似泊松分布。为便于计算,将居民出行距离以乘坐站点数量的方式转换,设Qab为在出行距离影响下选择乘坐公交的乘客从a站点上车前往b站点下车的概率,λ为研究线路乘坐公交车的乘客人均乘坐站点数,当人均乘坐站点数大于在a站点之后的站点数量的情况下,采用λ=I-a來计算每站的下车概率:
Qab=e-λλ(b-a)(b-a)!(14)
2)站点换乘能力影响
对于需要换乘的乘客,站点可换乘线路数量越多,满足其换乘需求可能性就越高。同时,在换乘阈值内的异站换乘也需要考虑。设Li表示第i站及其500 m范围内其他站点可供出行人员换乘线路总数,Fi表示第i站换乘系数:
Fi=Li∑Ii=1Li(15)
3)站点出行吸引强度影响
全天候出行人员的公交出行规律呈现明显往返性,站点发生量越大,其吸引量也越大。设每站上车人数所对应吸引强度为Wi,有
Wi=Ai∑Ii=1Ai(16)
式中:Ai表示第i站上车人数。
4)站点周围土地利用性质影响
当一个站点附近为住宅用地时,一天出行结束后返程时间段在该站点下车的几率会增加。同理,工厂、政府办公区域、学校等土地利用性质会影响不同出行目的人群下车站点选择。设i站点以500 m为半径区域里有H种土地利用性质,用Gih作为i站点第h种土地利用性质面积比,gh表示相对应吸引系数,Ri表示第i站土地利用性质影响强度值,得
Ri=∑Hh=1Gih×gh,h=1,2,3,…,H (17)
本文结合其他学者[15-16]的研究,将线路土地利用现状分为6类,设住宅用地吸引强度为1,对比确定其他分类的吸引强度如表1所示。
3 实例分析
选取福州市125公交线路晚高峰(17:00—19:00)上行方向各站点上、下车客流进行跟车调查,统计各站点的上下客人数,与识别人数进行对比。根据跟车调查,125路公交的乘客投币人数与免费人数约占20%,考虑推算过程中的部分客流损失,将识别得到的客流量以1.3倍进行扩样对比。
3.1 上车站点匹配结果
为验证站间缺失数据修正的准确性,选取福州市41公交线路3月13日至17日的100个到离站数据完整、工作日班次已经过误差时间修正的公交GPS数据及对应的公交刷卡数据,其中一半班次为7点至9点、17点至19点的高峰时期,另一半为随机平峰时段。每个班次任取一站有乘客上车的到离站数据清空,一站无乘客上车的数据清空,共计200条待修复到离站数据。以一周内工作日其余班次数据作为历史数据集合,根据模型对到离站数据进行修复,并与删除的原到站时间进行对比,结果如表2所示。
从表2可以看出,当缺失站点有乘客刷卡上车时,在任何情况下模型计算结果误差均在3 s左右;当缺失站点没有乘客时,模型计算结果误差增大,高峰时段的误差值最大,造成这种计算结果的原因是高峰时段路况不佳,交通延误较大,行程时间波动较大。由于站间数据缺失修复是为了客流特征挖掘服务,针对的是有乘客刷卡上车时乘客上车站点的识别,因此在有乘客刷卡条件下的模型修复计算结果误差均较小,计算结果用于公交刷卡数据与公交GPS数据的数据融合是可行的。
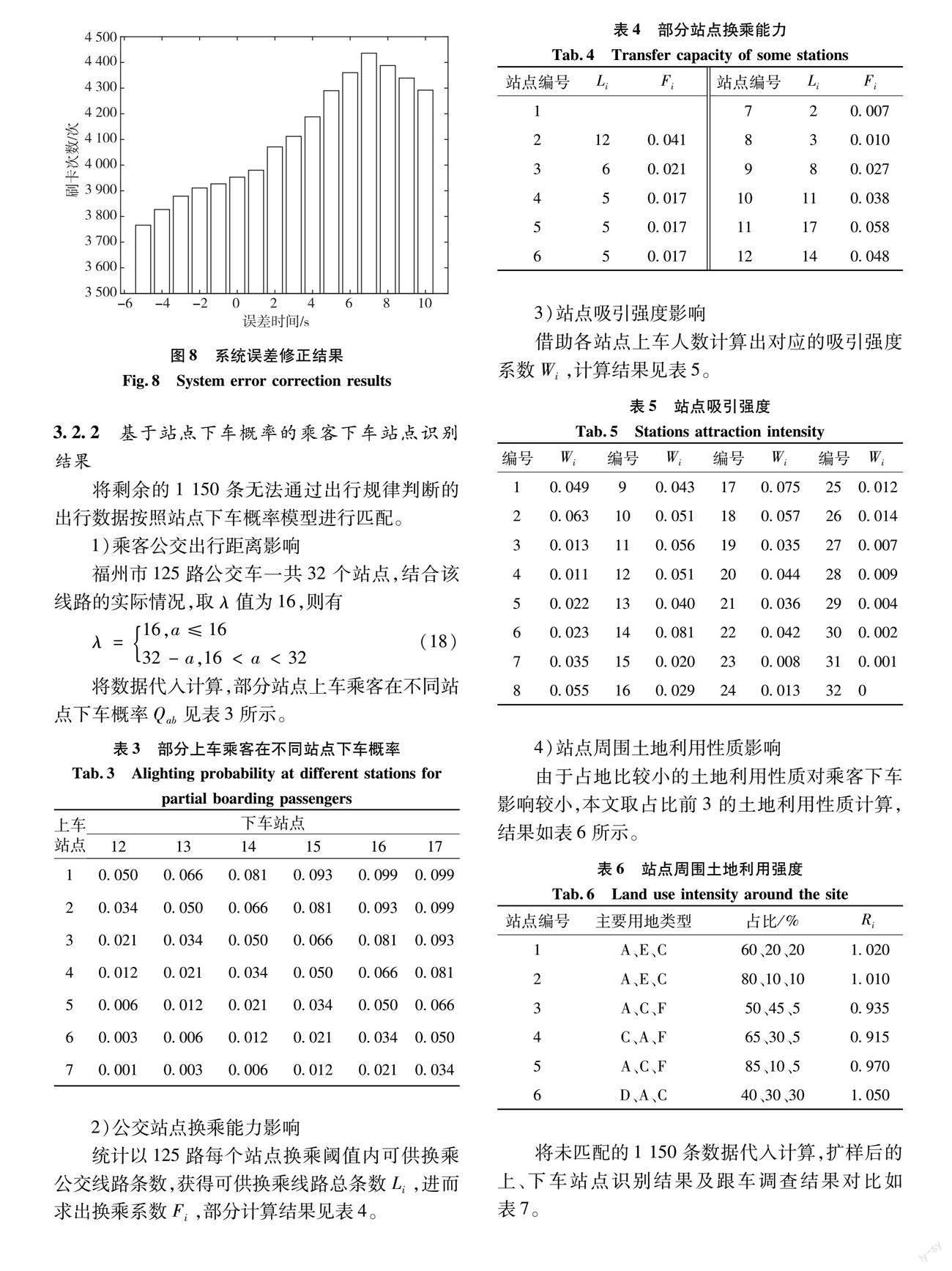
如图8所示,将未经处理的数据直接采用上车站点识别方法进行时间匹配,匹配成功3 953次,在通过刷卡数据与公交GPS到离站数据相差+7 s的系统误差修正及站间数据修复后,匹配成功4 436次,匹配成功率较未经处理的匹配人数提高了12.22%。
3.2 下车站点匹配结果
3.2.1 基于出行规律的乘客下车站点识别结果
计算结果中符合集合U1条件的数据1 532条,符合集合U2的数据1 398条,查看往日出行记录后符合出行规律条件的353条,模型匹配量占总量的74.1%。造成乘客数据没有识别成功的原因一是当日乘客出行属于偶然出行,往日记录中不存在能匹配的出行规律,二是存在部分乘客的刷卡数据与站点不匹配,属于无效数据。
3.2.2 基于站点下车概率的乘客下车站点识别结果
将剩余的1 150条无法通过出行规律判断的出行数据按照站点下车概率模型进行匹配。
1)乘客公交出行距离影响
福州市125路公交车一共32个站点,结合该线路的实际情况,取λ值为16,则有
λ=16,a≤1632-a,16<a<32 (18)
将数据代入计算,部分站点上车乘客在不同站点下车概率Qab见表3所示。
2)公交站点换乘能力影响
统计以125路每个站点换乘阈值内可供换乘公交线路条数,获得可供换乘线路总条数Li,进而求出换乘系数Fi,部分计算结果见表4。
3)站点吸引强度影响
借助各站点上车人数计算出对应的吸引强度系数Wi,计算结果见表5。
4)站点周围土地利用性质影响
由于占地比较小的土地利用性质对乘客下车影响较小,本文取占比前3的土地利用性质计算,结果如表6所示。
将未匹配的1 150条数据代入计算,扩样后的上、下车站点识别结果及跟车调查结果对比如表7。
3.3 站点识别准确性验证
平均绝对误差(mean absolute error,MAE)及均方根误差(root mean square error,RMSE)作为验证预测值与实际值偏差情况的评价指标被广泛应用,在本文中计算公式分别表示为:
EMA=1I∑Ii=1Psi-Pfi×100%(19)
ERMS=1I∑Ii=1(Psi-Pfi)2×100%(20)
式中:EMA为平均绝对误差,ERMS为均方根误差,Psi为i站点实际上、下车人数;Pfi为i站点识别方法求得的上、下车人数。
将扩样后数据与跟车调查数据进行对比,并带入式(19)、(20),结果见图9及表8。
从图9及表8中可以看出,实际调查的客流情况与模型识别结果基本吻合,扩样后的上车站点识别值与实际值相比,MAE值为3.59%,RMSE值为4.19%,二者误差小,均为可接受的误差范围,扩样后仍然存在一定误差的原因一方面是在数据匹配过程中存在小部分的无效数据及无法匹配数据,另一方面是因为小部分乘客的公交出行具有偶然性,因此存在一定的誤差;扩样后的下车站点识别值与实际值相比,MAE值为5.03%,RMSE值为5.79%,二者误差小,均为可接受的误差范围,扩样后的误差大于上车站点识别结果的原因一方面是小部分乘客的公交出行具有偶然性,即使采用了下车概率进行补充,计算仍会存在一定误差,另一方面原因是上车站点识别本身具有误差,在下车站点识别时这一部分误差有一定的影响。综合看来,将基于此上下车站点识别准确率下得到的识别结果用于后续公交客流特征分析及公交调度优化研究是可行的。
4 结论
本文在对公交多源数据修正系统时间误差及修正站间缺失数据的基础上,提出了基于乘客刷卡时间与公交到离站时间的时间匹配方法解决站点信息不匹配情况下的乘客上车站点识别。将乘客按照是否具有出行规律,分别提出了基于乘客出行规律的乘客下车站点识别方法及乘客站点下车概率模型对下车站点识别方法进行补充。通过实例验证,结果表明:上车站点识别值与实际值相比,MAE值为3.59%,RMSE值为4.19%,下车站点识别值与实际值相比,MAE值为5.03%,RMSE值为5.79%,上下车识别误差小,均在可接受误差范围内,验证了上、下站点识别模型的有效性。此外,将在未来对无出行规律的乘客下车站点影响因素进行更多角度的研究,继续提高模型的识别精度。
参考文献:
LEE H, PARK H C, KHO S Y, et al. Assessing transit competitiveness in Seoul considering actual transit travel times based on smart card data[J]. Journal of Transport Geography, 2019, 80: 102546.
[2] EGU O, BONNEL P. Investigating day-to-day variability of transit usage on a multimonth scale with smart card data: a case study in Lyon[J]. Travel Behaviour and Society, 2020, 19: 112-123.
[3] TANG T L, LIU R H, CHOUDHURY C. Incorporating weather conditions and travel history in estimating the alighting bus stops from smart card data[J]. Sustainable Cities and Society, 2020, 53: 101927.
[4] CHEN Z, FAN W. Extracting bus transit boarding and alighting information using smart card transaction data[J]. Journal of Public Transportation, 2020, 22(1): 40-56.
[5] HUANG D, YU J, SHEN S Y, et al. A method for bus OD matrix estimation using multisource data[J]. Journal of Advanced Transportation, 2020. DOI: 10.1155/2020/5740521.
[6] 谢振东, 冷梦甜, 吴金成. 基于一卡通数据的公交站点识别方法分析与研究[J]. 广东工业大学学报, 2019, 36(1): 23-28.
[7] 邬群勇,苏克云,邹智杰.基于海量IC卡数据的公交客流时空分析[J].贵州大学学报(自然科学版),2018,35(6):93-98.
[8] 秦政. 基于数据挖掘的客流特征提取及公交调度优化研究[D]. 成都: 西南交通大学, 2017.
[9] 左快乐. 基于IC卡数据的不同时间层次公交客流预测方法与应用研究[D]. 南京: 东南大学, 2016.
[10]张文胜,卢梦,朱冀军.基于公交IC卡和AVL数据的公交客流OD推算[J].计算机应用与软件,2021,38(7):100-105.
[11]孙凯,郑长江.基于公交IC卡刷卡数据的站点客流推算[J].贵州大学学报(自然科学版),2021,38(2):104-110,124.
[12]常焕. 基于公交IC卡和AVL数据的公交换乘识别方法研究[D]. 成都: 西南交通大学, 2019.
[13]傅准. 城市公共交通换乘客流时空分布可视化及站点聚类分析[D]. 广州: 广东工业大学, 2019.
[14]柳伍生, 周向栋, 谭倩. 多元數据下的公交站点客流不确定性分析[J]. 交通运输系统工程与信息, 2018, 18(2): 149-156.
[15]赵鹏. 基于成都公交IC卡数据的乘客上下车站点推算方法研究[D]. 成都: 西南交通大学, 2015.
[16]赵志恒. 基于公交IC卡数据的城市公交站点客流测算方法研究[D]. 哈尔滨: 东北林业大学, 2019.
(责任编辑:曾 晶)
Passenger Boarding and Alighting Station Identification
Based on Transit Data Mining
ZHANG Jie, TANG Yaohong*, YUAN Qiufeng, WANG Wei
(College of Information and Electrical Engineering, Ningde Normal University, Ningde 352100, China)
Abstract:
In order to develop a bus scheduling plan that meets the passenger flow, increase the attractiveness of bus travel and reduce the carbon emission of private car travel, it is necessary to propose an accurate passenger boarding and alighting station identification method to obtain accurate passenger flow data and provide fine data support for bus scheduling. This paper proposes a data pre-processing method for system time error correction and station-to-station missing data repair based on multiple sources of regular bus data in Fuzhou City. On this basis, the method of identifying the boarding point by matching the passenger swipe time with the bus arrival and departure time is proposed. According to the travel behavior of passengers, we propose the identification method of passenger alighting stations based on the travel pattern and the identification method of passenger alighting probability under the influence of travel distance, interchange ability, travel attraction intensity and the nature of surrounding land use. Finally, the identification data is compared with the actual survey data to verify the accuracy of the identification method, taking the Fuzhou 125 bus data as an example. The research results can provide a data mining method for urban bus passenger flow OD survey, reducing the manpower and material resources generated by traditional survey, and offering data support for the operation and scheduling of bus enterprises.
Key words:
urban traffic; station identification; travel law; data mining

