基于模糊层次分析法的高等数学课程思政教学评价体系的构建

■ 新乡学院数学与统计学院 周 霖

1 模糊层次分析法

层次分析法（Analytic Hierarchy Process，简称AHP），是一种将影响决策的因素分解成目标、准则、方案等层次进行定性和定量分析的决策方法，在20世纪70年代由美国运筹学家托马斯·塞蒂（T.L.Saaty）提出，现在已被广泛应用于经济、军事、农业、教育、医疗和环境等领域，模糊层次分析法是将模糊分析法和层次分析法相结合的评价方法。

模糊层次分析法的相关定义如下：

定义1：矩阵R＝(rij)n×n，若满足0≤rij≤1，(i，j＝1，2，…，n)，则R称为模糊矩阵。

定义2：若模糊矩阵R 满足rij+rji＝1，(i，j＝1，2，…，n)，则称此模糊矩阵为模糊判断矩阵A，它是通过两两元素重要度相互比较得到的，一般采用的是0.1-0.9九级标度法（见表1）。

定义3：若模糊矩阵R满足∀i，j，k有

则称模糊矩阵R为模糊一致矩阵。

定义4：由模糊一致矩阵采用行和归一，求得的排序向量为w＝(w1，w2，…，wn)T，需满足下式：

2 基于层次分析法的高等数学课程思政教学评价体系的构建

2.1 建立高等数学课程思政教学评价体系

根据研究目的设计访谈纲要，笔者对新乡学院部分师生进行访谈，了解影响高等数学课程思政教学质量的因素，最后经专家讨论形成高等数学课程思政教学评价体系。该体系分为教学设计、教学内容、课堂组织和教学效果4个一级指标和12个二级指标。为了便于运用模糊层次分析法进行各指标权重设置，笔者将一级指标（准则层）和二级指标（子准则层）进行编码，具体指标内容及编码见表2。

表2 高等数学课程思政教学评价体系

2.2 运用层次分析法确定各指标的权重

笔者根据设计的高等数学课程思政教学评价体系制订调查表，分别向5名思政专业背景、5名教育学背景和5名数学专业背景的专家发放。专家结合自身的专业知识和教学经验，依照标度法，对一级指标和二级指标等因素进行判断和比较（见表3），再根据打分结果建立对应的模糊判断矩阵。

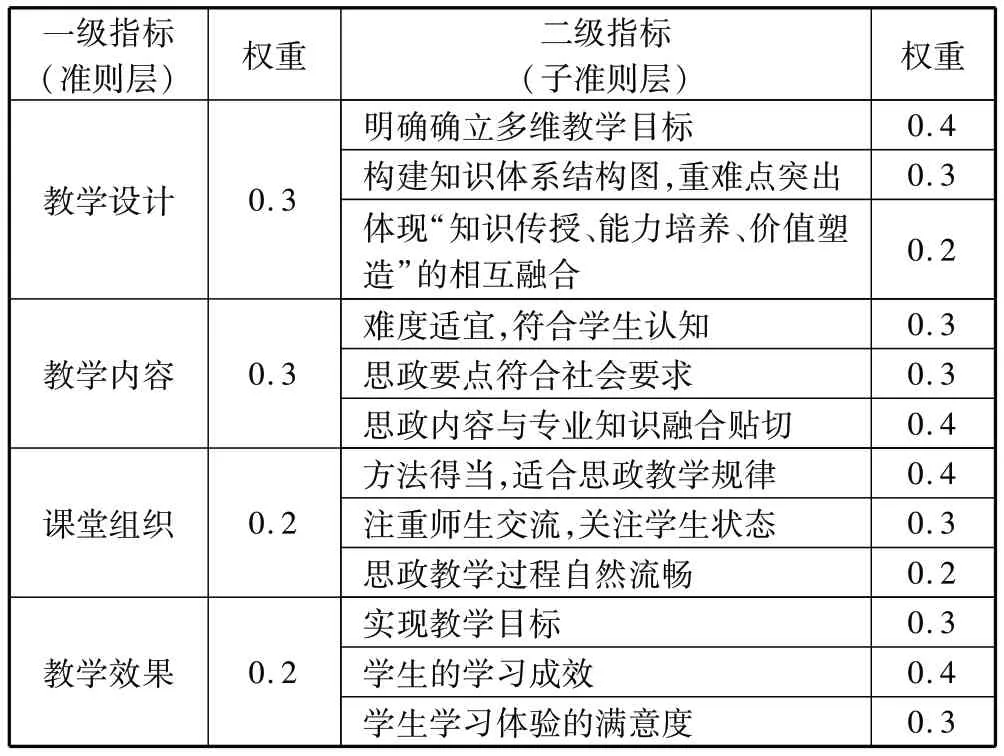
表3 专家测评统计表

教学设计、教学内容、课堂组织、教学效果的模糊判断矩阵为R1-R4。

根据定义3计算模糊一致矩阵R( B1) -R( B4) 和R( A )。

显然这5个模糊一致矩阵满足一致性，根据定义4计算各指标的权重，笔者得出高等数学课程思政教学评价体系权重（见表4）。

表4 高等数学课程思政教学评价体系权重

2.3 运用模糊综合评价方法进行评价

根据构建的高等数学课程思政教学评价体系，笔者运用模糊综合评价法，对教师的教学质量进行评价。模糊综合评价法通常分为以下三个步骤。一是确定评价对象的因素集合、设立评价等级，建立模糊集合；二是通过层次分析法确定权重向量，从而构建出评价矩阵；三是利用模糊矩阵的合成计算，进行综合评价。笔者根据专家组对教师甲的教学评价建立模糊评价矩阵，教学设计、教学内容、课堂组织、教学效果的模糊评价矩阵为S1-S4。

由公式Bi＝Wi×Si（i＝1，2，3，4）得出高等数学课程思政教学评价体系一级模糊评价矩阵为：

运用B与前面通过层次分析法求得的权重W＝（0.317 0.233 0.233 0.250）进行模糊矩阵的复合运算，

B×W＝（0.7890 0.2141 0.0442 0）

最后将评价集V＝(V1，V2，V3，V4)＝（优，良，中，差），若按分数计算，

取优＝95，良＝85，中＝75，差＝60，得出专家对该教师的综合评价。

F＝B×W×VT＝96.47。

3 结语

本文构建的高等数学思政课程教学评价体系的评价指标较少，今后还需要在实践中不断完善，以提升教师的思政育人能力，落实立德树人的根本任务。