立足物理模型，发展科学思维
——以斜面模型及其变式教学为例

2023-12-13 02:51:22张辉

物理教学探讨 2023年11期

张辉

甘肃省酒泉中学，甘肃酒泉 735000

《普通高中物理课程标准（2017年版2020年修订）》明确要求教师要注重“培养学生的模型建构等物理学科核心素养”，并能够“根据本模块物理模型的特点，联系生产生活实际，从多个角度创设情境，提出与物理学有关的问题，引导学生讨论，让学生体会建构模型的必要性及方法”［1］，在解决问题的过程中，提升学生的科学素养。

高中物理教学中有很多理想模型，这些物理模型有的是研究对象的理想化，如质点、点电荷等；有的是基于研究对象所处的条件而形成，如光滑的斜面、恒力、真空、匀强电场等；还有的是“运动变化过程的理想化模型，如匀变速直线运动等”［2］。

一般来说，物理模型的建构需要以下过程：首先，需要分析确定实际问题中的研究对象或过程，“把握建立模型的物理需要”，如为什么要将物体抽象为质点；其次，需要准确分析把握实际物体或过程的主要因素和次要因素，做出准确、科学的提炼，将主要方面凸显出来；第三，要基于主要因素分析其本质特征，进行科学合理的抽象，并与已知的物理模型进行比较，符合条件则可以建立相应的物理模型；最后，利用建构的物理模型解决实际问题，在解决问题的过程中进一步概括、检验、修正完善物理模型。

高中物理经常研究物体在斜面上的运动情况，这类问题结合了质点模型、斜面模型和直线运动模型，常以物体在斜面上静止或沿斜面的运动作为基础情境，考查运动与相互作用观念，动量、能量观念等。这就要求教师“在教学中要引导学生体会建构质点、直线运动等物理模型的过程，深刻理解物理模型的使用条件”［1］，并在解决实际问题的过程中，突出主要因素，忽略次要因素，通过分析概括构建恰当的物理模型，应用模型分析解决问题，体会并逐步掌握和内化构建物理模型的思路方法，发展其科学思维。

本文将结合了质点模型、斜面模型和直线运动模型的综合模型称为斜面基本模型，并以斜面基本模型为骨架设置系列变式问题，通过分析简单实际问题引导学生经历“比较—概括—抽象”的过程，识别和构建模型，并在构建斜面基本模型的基础上通过模型的直接变式训练“引导学生经历多角度理论探究，充分应用不同的物理观念思考问题，在解决问题的过程中发展学生的科学思维。”［1］

1 关注实际情境，构建物理模型，培养基本能力

物理问题来源于生产生活的实际情境，将实际情境转化为解决问题的物理情境，建立相应的物理模型，是分析解决问题的关键。教师可以用如下问题情境来引导学生构建斜面基本模型。

【例题1】新疆丝绸之路滑雪场第一雪道“玄奘”长2600 m，最大坡度段倾角约37°，长约500 m，某滑雪运动员进入该段的速度约为10 m/s。雪道摩擦力约为该运动员重力的五分之一。求解运动员离开该段的速度及在该段所用的时间。

分析：上述问题最终要求解运动员在运动过程中的末速度和运动时间，解决这一问题的基本思路是分析构建匀加速直线运动模型，求解加速度，进而由运动学公式解决问题。问题的难点是对运动员进行受力分析，因而需要先构建质点斜面模型。为此，教师应首先引导学生复习质点的定义和研究对象可以被抽象为质点的条件，引导学生比较该问题情境中的运动员和质点模型，明确可以将上述问题情境中在较长雪道上滑雪的运动员视为质点；再引导学生将坡度约为37°的滑雪道抽象为倾角为37°的理想斜面，进而可将该问题中的运动员和雪道概括起来，抽象成质点在理想斜面上的运动模型。在构建质点在斜面上这一基本模型后，教师指导学生对质点进行受力分析和运动分析，利用动力学观点求解加速度，列出运动学方程，即可解决运动过程的末速度与所用时间问题。

在解决上述问题的基础上，教师提示学生联想生活情境中的“斜面模型”，学生通过联想举出实例，如小孩从长滑梯高处向下滑的过程，汽车下长坡的过程，货车上的货物通过斜传送带送到地面的过程，游客乘坐滑沙板滑沙的过程等，并明确通过比较、概括和抽象，可以将以上实际问题情境转化成基本的斜面模型来处理。

斜面模型中蕴含着处理该类问题的基本思路和方法，这些思路与方法是解决物理问题的根本。因此，在教学中教师要重视对学生基本能力的培养。教师可以通过指导学生画出示意图，确定合适的物体作为研究对象，分步骤准确画出研究对象的受力分析图，列出平衡方程或牛顿第二定律等，在逐步解决问题的过程中帮助学生理清基本思路，规范解题步骤，指导学生掌握依次应用力与运动的观点、动量和功能关系的观点解决问题的一般方法。让学生通过试错发现技能薄弱点并巩固训练提升，从而提高处理问题的基本能力。

2 加强变式训练，提升复杂情境下的受力分析能力

受力分析能力是学生学习高中物理必备的关键能力之一。对研究对象准确、全面地进行受力分析往往是解决问题的关键。在复杂的斜面模型问题中，受力分析是解决问题的难点之一，在构建斜面基本模型的基础上，通过变式训练，引导学生通过多情境受力分析训练，总结受力分析的思路方法与分析技巧，可以破解难点，提升其受力分析这一关键能力。

在解决例题1 的过程中，已经构建了斜面模型，教师可以在此基础上给出如下变式问题：

【变式1】质量为m 的物块在倾角为θ 的固定斜面上处于平衡状态。物块受哪几个力？大小与方向如何？请画受力分析图并列式求解。

教师可以引导学生自主画出示意图，引导学生审题，得出物块有可能在斜面上静止或者沿斜面匀速下滑，再引导学生分情况作出物块的受力分析图，列出平衡方程，求解斜面对物体的支持力和摩擦力。学生得出物体静止时所受摩擦力为静摩擦力，匀速下滑时受到的摩擦力为滑动摩擦力，但是大小都等于重力沿斜面向下的分力。并对两种情况下得出的结论进行总结讨论和交流。

通过变式1 的解决过程，引导学生初步体验斜面模型的基本分析方法和思路，即对斜面上的物体进行受力分析和运动分析，从而引导学生形成正确的运动与相互作用的物理观念。然后，可以通过变式2 引导学生养成从基本思路和方法出发，通过分析综合解决复杂问题的思维习惯。

【变式2】如图1所示，若质量为m 的物块原来静止在固定的倾角为θ 的斜面上，最大静摩擦力大于mgsinθ，现在沿斜面方向施加外力F，物块仍然能够静止在斜面上，求F 的变化范围。

图1 变式2 情境图（图中所示为F 向上的情况）

教师首先引导学生认识该问题仍然是物体在斜面上的平衡问题，因而解决问题的基本思路是对物体进行受力分析。学生得出物块在沿斜面向下的方向必然受到重力的分力，大小为mgsinθ。教师引导学生思考最大静摩擦力大于mgsinθ 的含义。学生思考得出外力F 的方向可以沿斜面向下，使F1+mgsinθ=Ffmax，此时，静摩擦力沿斜面向上达到最大值，物块恰好处于静止状态；若F 沿斜面向上从零逐渐增大，则静摩擦力先沿斜面向上逐渐减小至零，再随着F 继续增大而变成沿斜面向下并达到最大值，此时F2=mgsinθ+Ffmax，由此得出外力F 方向与大小的变化范围。

通过变式2 的分析讨论，学生不仅能够在沿斜面方向三力平衡分析中进一步掌握物体的平衡条件，还能够在力的动态变化过程的分析中深刻理解静摩擦力的被动性，顺利突破问题的难点。

在上述分析的基础上，教师可以对问题继续进行变式，引导学生加深理解，形成关键能力。

【变式3】若质量为m 的物块原来静止在固定斜面上，斜面如图1所示，物块所受最大静摩擦力等于滑动摩擦力，现在对物块施加水平向右的外力F，物块仍然能够静止在斜面上，求水平力F 的变化范围。

教师引导学生分析变式2 和变式3 情境的区别。学生得出变式2 中作用在斜面上的正压力不变，所以最大静摩擦力的大小也不变，变式3中由于水平外力变化，物块对斜面的正压力也会随之改变，因而最大静摩擦力的大小也会变化。当水平外力最大时，其沿斜面向上的分力最大，此时最大静摩擦力沿斜面向下；当水平外力最小时，其沿斜面向上的分力最小，此时最大静摩擦力沿斜面向上。教师指导学生通过将水平外力和重力分解到沿斜面和垂直斜面两个方向，再分别列出两个方向的平衡方程，就可以解出水平外力的变化范围。

教师再引导学生总结问题2 与问题3 的共同点，学生讨论交流，得出两道题目都以斜面上的物块在不同情境中的受力平衡为载体，着重考查了静摩擦力的被动性，即随着外力变化，静摩擦力的大小和方向都可能发生变化。

通过3 个变式训练，引导学生研究物体在斜面上的受力平衡问题，从二力平衡到三力平衡，从恒力作用下的平衡到变力作用下的平衡问题，由简入深，由易到难，逐步引导学生掌握处理斜面上物体平衡的基本方法，感悟物体在斜面上恰好平衡的临界状态和最大静摩擦力的关系，深刻理解静摩擦力的被动性这一受力分析的难点，从而提升受力分析这一关键能力。

3 加强重要方法应用训练，提升学生科学思维能力

基本模型蕴含着基本方法和思路，在基于基本模型进行变式训练过程中重视方法和思路的应用与总结，可以有效提升学生的科学思维水平。

在前述三个变式问题的基础上，教师继续给出变式训练如下。

【变式4】若质量为m 的物块在粗糙的倾角为θ的斜面体上以加速度a 加速下滑，斜面体质量为M 且不固定，斜面体能够静止在水平地面上，地面对斜面体的支持力FN大小如何？地面对斜面体有摩擦力吗？若有，方向如何？大小如何？

抛出问题后，教师引导学生分别分析斜面体和物块的运动状态，明确斜面体静止而物块沿斜面向下加速运动，二者运动状态不同，可以用隔离法分别以物块和斜面体为研究对象进行受力分析，培养学生在复杂情境中准确选取研究对象的能力。学生对物块进行受力分析时，教师提示学生物块沿斜面向下加速运动，说明物块所受的合力沿斜面向下，因而需要在加速度方向和垂直加速度方向建立直角坐标系，得到物块所受沿斜面和垂直斜面的力。然后，在沿斜面方向列出牛顿第二定律，在垂直斜面的方向列出平衡方程，即可解出物块所受的力。学生在这一过程中进一步形成正确的力与相互作用的观点，进一步明确隔离法受力分析的基本思路，提升其物理基本素养。教师引导学生得出斜面体对物块的两个力，分别是斜面体对物块的支持力和摩擦力，进而启发学生对简单物体进行受力分析就可以根据牛顿第三定律得出简单物体对复杂物体的反作用力的大小和方向。引导学生隔离斜面体进行受力分析，根据斜面体处于静止状态时受力平衡，得到地面对斜面体的支持力与摩擦力。在引导学生解答之后，教师可以板书展示隔离法的解答过程，引导学生总结隔离法的基本思路，强调解题细节，如三角函数的应用，物块对斜面体的两个反作用力的水平分力大小的比较等。

之后，教师可以引导学生从整体法的角度考虑，由于本题情境中物块和斜面体的运动状态不同，教师需要引导学生打破两物体加速度不同不能使用整体法的思维壁垒，对整体进行受力分析，从整体视角得出整体中的一部分（物块）有加速度必然是整体所受合外力不为零的结果，将物块沿斜面向下的加速度分解到水平和竖直两个方向，在这两个方向上对整体分别列出牛顿第二定律如下：

水平方向上：Ff=macosα，竖直方向上：Mg+mg-FN=masinθ。从而解决地面对斜面体的摩擦力大小和方向，顺利求解地面对斜面体的支持力大小。

在解决问题的过程中，教师应提问引导、画图示范，解决问题后指导学生总结隔离法和整体法的一般思路和方法。隔离法一般将物体所受的力分解到加速度方向与垂直加速度的方向，二次隔离强调从简单物体到复杂物体依次进行隔离法受力分析，根据牛顿第三定律判断简单物体对复杂物体的反作用力的大小和方向，结合研究对象的运动状态判断力的有无与方向，形成比较清晰的二次隔离法受力分析思路；对整体进行受力分析时，引导学生从整体的视角分析问题，打破两物体加速度不同不能使用整体法的思维壁垒，有效避开了研究对象内部的复杂分析过程，开阔学生进行受力分析的思路。尤其是在经历隔离法训练基本能力的基础上，多尝试利用整体法的观念和思路分析解决问题，既能夯实基本能力，又可以引导学生总结其内在规律，把握本质属性，从而有效提升其科学思维水平。

4 利用问题链多角度创设问题情境，提升学生分析综合能力

在基于斜面基本模型进行变式训练时，要注重基于不同物理观念创设问题情境，利用问题链合理设置梯度引导学生，从而促进物理观念在学生头脑中提炼升华，提升其分析综合能力。

【变式5】如图2所示，质量为M 的斜面体放在光滑水平面上，斜面的上表面也光滑。质量为m 的物块在斜面上由静止释放，则物块下滑的过程中，物块的机械能如何变化？

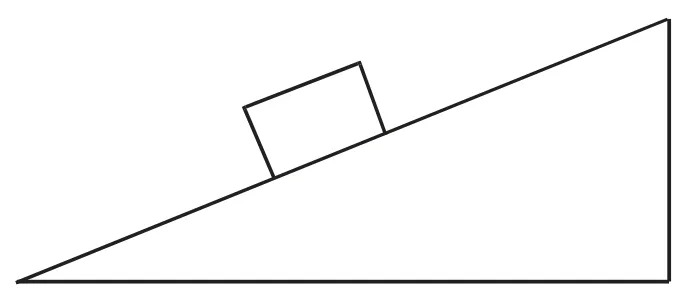
图2 变式5 情境图

要解决这个问题，教师可以设置梯度问题链，引导学生逐步思考探究，层层深入，从而解决问题。

（1）物块在光滑的斜面上受到哪些力？

教师引导学生画出受力分析图，得出物块受重力和斜面的支持力。

（2）物块受到的支持力FN的施力物体是谁？由牛顿第三定律能得到什么结论？

斜面对物块施加了力FN，由牛顿第三定律，物块给斜面一个反作用力FN′。

（3）斜面体所受合力方向如何？它将如何运动？

教师引导学生隔离斜面体并进行受力分析，分析发现在竖直方向合力为零，水平方向所受合力水平向右，将向右运动。

（4）若以物块与斜面体整体为研究对象，整体在水平方向受力如何？整体在水平方向动量如何变化？

以整体为研究对象，其在水平方向没有施力物体，所受合外力为零，整体在水平方向上动量守恒，因为水平方向初速度为零，整体的质心在水平方向上位置不变，物块在水平方向上相对地面向左运动，斜面体向右运动。

教师引导学生以受力分析为基础利用动量观点思考问题，使学生养成从受力、运动、动量、功能关系等角度分析问题的基本思路，提升学生的高阶思维水平，提高其解决问题的能力。

（5）请画出物块与斜面体在相对运动过程中某一时刻的运动示意图。

教师提示学生注意整体的质心在水平方向位置不变，而竖直方向上要向下移动，引导学生作出该过程中物体的合位移方向，利用运动示意图像促进学生深度理解系统水平方向动量守恒，同时培养学生的作图意识，提升作图的能力以及多方法、多角度综合分析问题的能力。

（6）请结合物块的受力分析图与运动示意图判断物块所受的重力与支持力的做功情况，以及物块与斜面体的机械能变化情况。

教师引导提示，学生讨论交流，得出重力对物块做正功，物块所受支持力的方向与物块运动方向之间的夹角为钝角，支持力对物块做负功。因为除了重力之外，支持力做了负功，故而物块的机械能减小；对于斜面体，它所受物块的反作用压力有水平分力，对斜面体做正功，使斜面体的动能增大，机械能增大；物块减小的机械能转移给了斜面体，但是因为系统没有摩擦力，物块和斜面体组成的系统机械能守恒。

通过应用问题链递进式引导学生不断将问题情境转化为探究过程，从简单的受力分析和运动分析出发，结合动量和功能关系的观点，综合应用隔离法、整体法，引导学生多视角探究解决问题，在不断的变式训练中拓展思维，形成大量的经验，提升分析综合能力和科学思维水平。

5 反思总结

构建物理模型对“认识和解决物理问题有重要意义”［1］。基于真实生活情境，抓住问题的主要方面，忽略次要因素，通过分析、比对、概括抽象构建物理模型，有助于培养学生利用物理模型解决问题的意识，提升其模型建构能力。此外，还有利于引导学生将模型建构的过程细化，本案例中将构建斜面模型的过程细化为质点模型的复习回顾，引导学生感知情境，分析滑雪道和运动员，将实际滑雪情境与理想斜面上滑块运动模型进行比对，最后将运动员在雪道上的运动抽象概括、组合完善为斜面基本模型。教师引导学生深度参与物理模型建构的全过程，能有效提升其物理建模能力和科学思维水平。

在构建了斜面基本模型的基础上，进行变式训练，由简单的问题情境入手，逐步推进至综合性问题，在多情境、多视角的探究过程中，建立经验，用具有引导性和梯度性的问题“有效降低学生学习的难度，增强变式训练的逻辑性，扩展思维链的长度，增强思维的深刻性，提升学生的思维能力”［3］。

在变式训练问题的设计与解答的过程中，应突出主要问题，以受力分析为例，将这一核心主线贯穿于变式训练的全过程，教师引导学生应用整体法、隔离法、正交分解法等作受力分析图，让学生充分试错、订正、纠错，促使学生抓住学习的重点、难点、易错点和主干问题，进行深度学习，使知识内容和思路方法都能体系化、明晰化，进而融会贯通，去伪存真，剖析问题本质，吃透并灵活选用物理知识和规律解决问题，培养学生思维的严谨性和深刻性，提升思维水平。