面向XRF的竞争性自适应重加权算法和粒子群优化的支持向量机定量分析研究

程惠珠, 杨婉琪, 李福生*, 马 骞, 赵彦春

1. 电子科技大学自动化工程学院, 四川 成都 611731 2. 电子科技大学长三角研究院(湖州), 浙江 湖州 313001

引 言

土壤作为生态系统基本要素之一, 是开展农业生产的关键性因素, 并为各行各业的发展提供必要场所。 随着工业化进程的不断推进, 一方面促进了各国经济水平的不断提升, 另一方面也不可避免的带来了严重的环境问题, 其中土壤污染已经成为比较棘手的问题[1-3]。 重金属污染在土壤环境污染中占据较大的比重, 其主要原因是重金属不能被土壤微生物所分解、 治理难度大、 化学性质稳定等而易于积累成为土壤无机污染物的重要组成部分[4]。 目前通常将土壤里毒性比较大的8种重金属元素Cu、 Pb、 Zn、 Cd、 Cr、 Ni、 As和Hg作为土壤污染筛查的对象。

高效、 准确、 便捷的土壤重金属检测方法对于了解土壤的环境状况以及开展污染防治工作具有重要的意义[5]。 X射线荧光光谱分析(X-ray fluorescence spectrometry, XRF)技术[6]由于具备快速、 准确、 无损等优势, 在检测元素成分含量中得到了广泛的应用。 由于通常需要检测的重金属含量很低, 导致元素的特征峰容易重叠或者受到其他元素的特征峰影响, 给检测分析带来较大误差。 随着人工智能算法[7-8]进入成分分析领域, 解决元素含量的精准测定出现了新思路。 任顺[9]等基于X射线荧光光谱结合多特征串联策略的ICO-CARS-SPA算法, 提升有效光谱信息贡献度。 刘峥莹[10]等利用麻雀搜索算法全局优化高斯混合模型中高斯峰的期望、 方差和权重参数, 实现重叠峰的分解。

本工作以土壤重金属为研究对象, 基于X射线荧光光谱分析技术对土壤中Cr、 Ni、 Cu、 Zn、 As、 Pb元素的检测方法进行了研究。 采集国家标准土壤样品的XRF光谱数据, 通过小波变换、 arPLS方法对原始光谱数据进行预处理, 并采用竞争性自适应加权算法的数据挖掘方法, 提取各土壤重金属元素的敏感能量特征段, 分别建立了基于敏感能量段的土壤重金属定量反演模型。

1 实验部分

1.1 样品与仪器设备

国家标准土壤样品均采购自国家标准物质网, 包含GBW、 GBW(E)、 GSD、 GSS系列的57个标准物质。 其中57个国家标准土壤样品中八大重金属元素含量范围如表1所示, 针对Cd、 Hg元素其含量大多集中在低含量区域内, 而所采用仪器的检出限在1 mg·kg-1, 因此主要考虑对于Cr、 Ni、 Cu、 Zn、 As、 Pb元素的定量分析。 国家土壤标准样品装杯后的示意图如图1(a)所示。 XRF光谱测量采用型号为TS-XH4000的手持便携式X射线荧光光谱仪如图1(b)所示。

图1 土壤样品和仪器的示意图(a): 土壤标准样品; (b): 手提式XRF光谱仪Fig.1 Schematic diagram of soil samples and instruments(a): Soil standard samples; (b): A handheld XRF spectrometer made

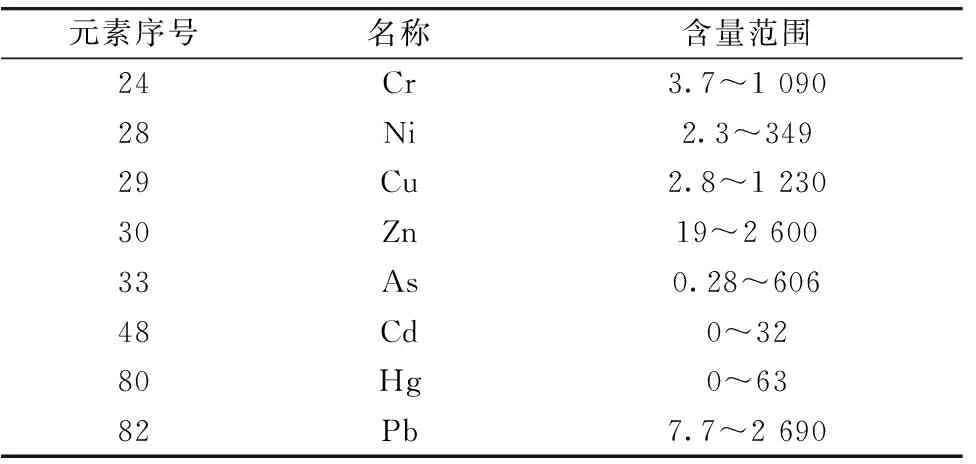
表1 57个国家标准土壤样品重金属元素含量范围(mg·kg-1)Table 1 Content range of heavy metal elements in 57 national standard soil samples (mg·kg-1)

1.2 光谱获取

为保证土壤光谱数据的稳定性, 在光谱仪允许的环境温度内, 对光谱仪选用土壤模式, 调整好土壤的最佳测试参数后, 对每个样品的测试时间设置为90 s。 并将同一个土壤样品测试3次取平均值, 作为相应样品最终的光谱数据。

1.3 数据分析及评价指标

1.3.1 CARS算法

竞争性自适应重加权算法[11-13]结合蒙特卡罗随机采样以及偏最小二乘回归算法的特征选择方法, 并通过获得交叉验证均方根误差最小的子集来获取最优的特征组合。 CARS法[14-15]的每个采样周期可分为4个连续的步骤, 包括: (1)利用蒙特卡罗采样法从校正集中选择一定数量的样本, 进行PLS建模; (2)计算通道能量段回归系数的绝对值权重, 利用衰减指数法剔除绝对值较小的能量段变量; (3)采用自适应加权算法在剩余的能量通道变量中选择能量段, 建立PLSR模型; (4)选择在均方根误差最小的模型对应的能量段变量作为最终的特征选择变量。

1.3.2 粒子群算法优化SVR模型

由于土壤的基体效应与谱线重叠干扰, 在实际分析测试中得到的元素谱线强度与浓度并不是呈现出完美的线性关系, 因此在对于元素做定量分析时, 需要考虑使用非线性模型建立光谱的反演预测。 SVM(粒子群算法)[16-17]作为机器学习中一种应用较为广泛的算法, 常用于解决非线性分类与回归问题。 考虑其泛化能力, 针对其中参数惩罚因子c、 核函数g的选取, 并且采用的是一种随机局部搜索策略--粒子群算法, 对最优的参数进行寻优。 模型预测的精度用决定系数(determination coefficients,R2)和均方根误差(root mean squard error, RMSE)来衡量。

2 结果与讨论

2.1 光谱数据预处理

针对XRF光谱的预处理, 利用Matlab中的ddencmp函数自动生成小波去噪的阈值选择方案, 小波选取为coif3, 并采用arPLS方法进行光谱的基线校正。 以Cu元素为例, 将原始信号与进行去噪和本底扣除后光谱信号的特征峰计数以及含量进行线性拟合如图2所示。

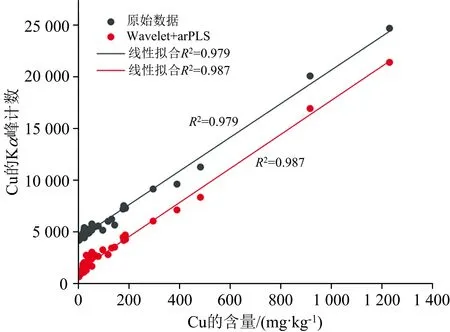
图2 Cu元素XRF光谱预处理前后特征峰含量拟合Fig.2 Fitting diagram of characteristic peak content before and after XRF spectrum pretreatment of Cu element

2.2 竞争性自适应重加权算法的特征选择

为了增加特征选择的稳定性、 可靠性, 对CARS算法的参数进行设定, 其中重复计算次数为2 048次, 校准样品与总样品的比率为0.8, 交叉验证的最大潜在变量数(即PLS主成分数)为15, 预处理法选择“center”, MCS抽样运行次数为50, 并采用5折交叉验证。 将57份经过预处理后的标准土壤样品作为输入, 即样品矩阵为57×2 048, 分别将Cr、 Ni、 Cu、 Zn、 As、 Pb元素的含量作为测试属性, 其矩阵大小均为57×1, 计算不同重金属元素在最小均方根误差下的特征能量段, 作为进行特征选择的结果。

图3为基于CARS算法针对Cu元素的能量段变量筛选过程。 图中“*”为RMSECV值最低点, 因此对于Cu元素, 在MCS抽样次数为30时, 获得的交叉验证均方根误差值最小。 在RMSECV值最低时, 此时保留的变量个数及其特征能量值如表2所示, 分析不同的元素筛选出的特征能量值。

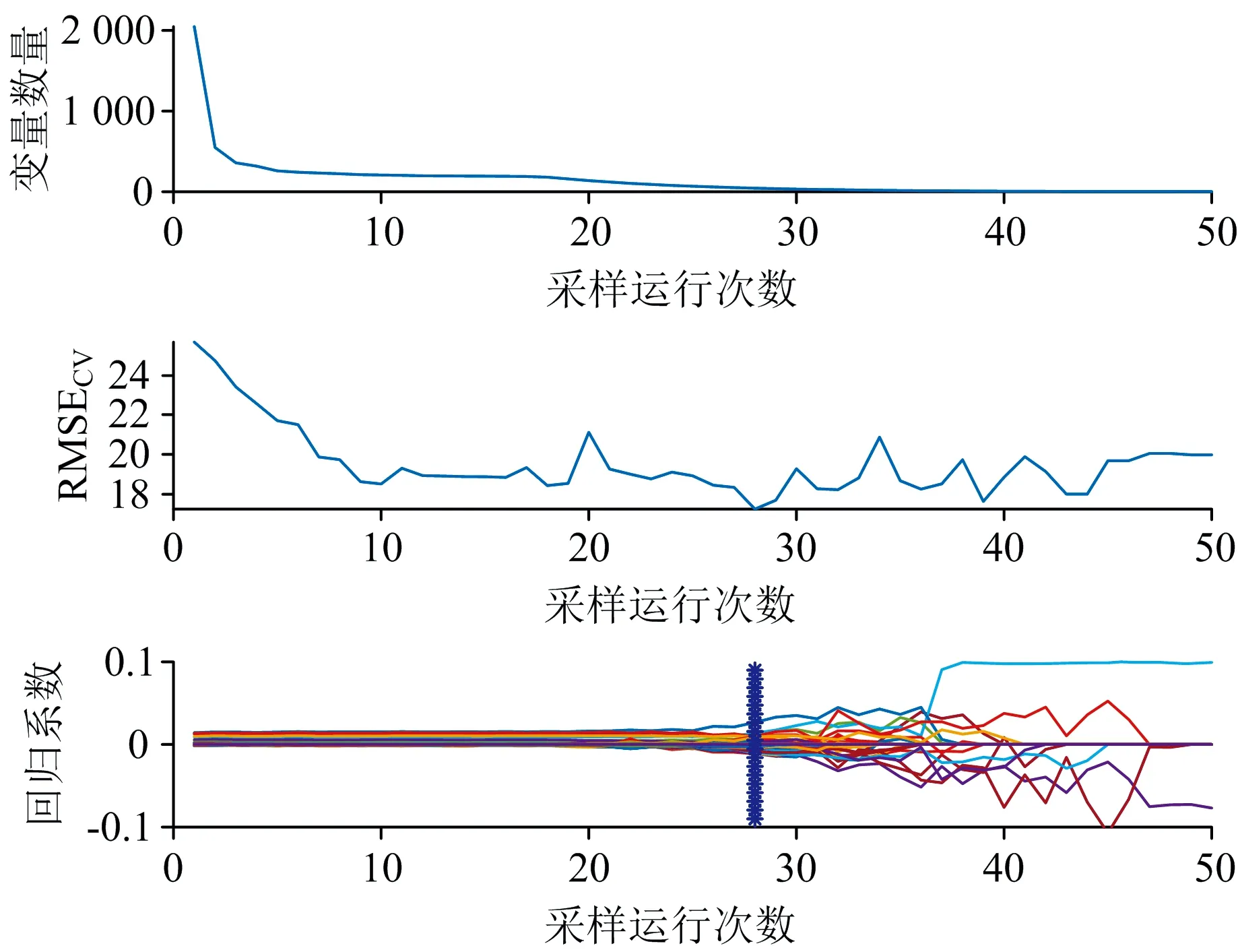
图3 CARS优选Cu元素特征能量过程Fig.3 CARS optimization of Cu element characteristic energy process

表2 CARS算法筛选出的特征能量Table 2 Feature energies screened out by CARS algorithm

根据表2, 针对Cr元素, 特征能量值主要集中在5.35～6.71 keV能量段及10.02～11.14 keV能量段, 由表3可知, 正对应Cr元素的特征峰能量段以及As元素的特征峰。 根据对于土壤的基体效应与谱线重叠干扰, 可知选取的特征能量值对应的特征元素, 除了待分析元素本身外, 部分还存在着土壤基体效应元素Fe, 以及相应的谱线干扰元素, 进一步说明了CARS算法在进行特征选择时的有效性。 同时, 经过基于CARS算法的特征变量选择, 变量的个数由2 048个变为9～29个, 为原来变量个数的0.43%～1.42%。

表3 土壤部分元素的特征峰能量范围Table 3 Characteristic peak energy range of some elements in soil

2.3 粒子群优化的SVR模型训练与预测分析

首先进行样本集划分, 将57份土壤标准样品划分为预测集合与训练集, 包括47份训练集与10份验证集。 对于粒子群算法设置其初始其参数分别为: 惯性因子0.5, 学习因子c1为1.5,c2为1.7, 迭代次数为100, 种群规模为50。 为了对PSO-SVR算法模型进行效果验证, 选择SVR、 PLSR模型进行对比。 同时, 为了说明基于CARS算法进行特征选择的必要性, 将未进行特征选择的元素特征峰计数值直接作为输入, 采用PSO-SVR算法进行含量分析, 得到不同定量反演方法的评估结果对比如表4所示。 首先对比PSO-SVR与CARS-PSO-SVR方法的效果, 可以看出未经过特征选择的PSO-SVR模型, 在训练集与预测集上的均方根误差更大。 在CARS算法的基础上, 对比PLSR、 SVR、 PSO-SVR模型的效果, 可以看出, 训练集的拟合程度均达到了0.988以上, 且RMSE均小于1, 预测集的拟合程度相对于训练集均有一定的下降, PSO-SVR模型的效果更好。

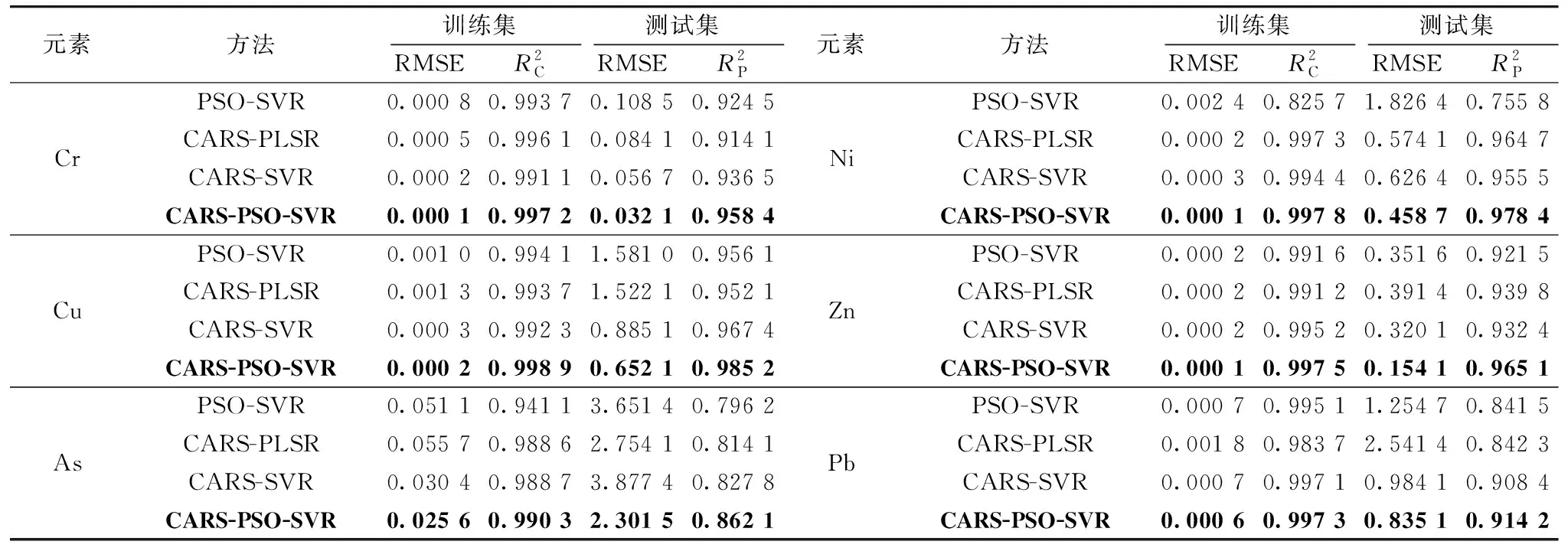
表4 不同定量反演方法的评估结果对比Table 4 Comparison of evaluation results of different quantitative inversion methods

3 结 论

土壤作为一种较为复杂的混合物, 其物理性质、 化学性质和不同的物质成分共同决定了光谱特征, 除此之外, 土壤中的重金属含量极低, 受到土壤基体效应以及谱线重叠的影响较大。 本文采用的特征输入为基于CARS的特征能量选择, 省略了针对特征提取繁琐的分析阶段, 简化了XRF光谱分析流程, 使得XRF光谱反演更加智能化, 并进一步分析特征能量峰的来源, 使得CARS选取的特征具备可解释性, 再采用PSO优化的SVR建立土壤重金属含量反演模型。