基于分数阶模型的隧道周围土体非线性流变固结分析

胡安峰，姜浩，肖志荣，谢森林，龚昭祺，李文乾

(1.浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058；2.浙江大学 平衡建筑研究中心，浙江 杭州 310058；3.浙江大学 建筑设计研究院有限公司，浙江 杭州 310028；4.浙江科技学院 土木与建筑工程学院，浙江 杭州 310023；5.浙江省建筑设计研究院，浙江 杭州 310006；6.中铁十局集团城市轨道交通工程有限公司，广东 广州 511400)

我国沿海和内陆地区广泛分布着软弱、高压缩性土体，在城市软土地层中建造完成的盾构隧道，会出现显著的长期沉降，通常占总沉降的30%～90%[1-3].隧道长期沉降不仅影响自身结构安全，还会对临近建/构筑物产生危害，如衬砌开裂和地面建筑倾斜，从产生机理来看，长期沉降主要受施工扰动引起的超静孔隙水压力逐步消散及土体本身流变特性的影响.此外，随着超静孔压逐渐消散，土体有效应力不断增加，孔隙比随之减小，渗透性和压缩性将出现非线性变化，这使得土体的固结分析更加复杂.因此，研究隧道周围饱和软土非线性流变固结问题具有重要的理论意义与工程应用价值.

詹美礼等[4]基于Terzaghi-Rendulic 理论利用Merchant 模型考虑土体流变，在盾构隧道完全透水和完全不透水条件下，获得周围土体流变固结以及地表沉降解析解.童磊[5]将Merchant 模型进一步推广至Burgers 模型.包鹤立[6]基于Li[7]给出的半渗漏边界条件考虑衬砌的均匀透水特性，揭示土体流变固结对隧道内力和变形的影响规律.刘干斌等[8]基于Biot 固结理论，考虑隧道半透水特性，给出饱和黏弹性土体中深埋隧道的固结解析解.曹奕等[9-10]引入e-lgk和e-lg σ 模型，并假设压缩性与渗透性同步变化，给出基于非线性方程的固结解析解.然而，在上述研究中均采用传统元件模型来考虑土体流变特性对固结发展的影响.Zhang[11]通过分析试验认为，传统元件模型难以描述黏弹性土体流变初始阶段特性.为了达到模拟精度，往往须增加元件个数进行组合，给工程应用带来不便[12].

分数阶黏弹性元件模型由Blair[13]和Gerasimov[14]首先提出，该元件模型采用分数阶导数代替整数阶导数描述元件的本构关系，使用相对较少的模型参数就能够模拟出较准确的材料流变特性[15-16].Caputo[17]给出新的分数阶导数定义，解决分数阶导数Laplace 变换的困难和相关初值问题，分数阶导数模型得以广泛应用.随着研究不断深入，Bagley 等[18]利用微积分表述分数阶黏弹性体的本构关系，而Koeller[19]利用微分对分数阶导数弹壶元件进行定义，拓展分数阶黏弹性元件模型应用范围.

近年来，国内一些学者利用分数阶导数元件模型进行土体流变固结相关的试验与理论研究.孙海忠等[20-23]利用分数阶的Kelvin 模型、修正Burgers 模型和Merchant 模型等对各地软土流变实验数据进行拟合，结果均具有高精度.另一部分学者基于分数阶导数模型研究土体固结性状，解益等[24-26]利用分数阶Kelvin 模型研究参数对土体固结过程中孔压消散以及沉降的影响；刘忠玉等[27]基于非达西流和分数阶Merchant 模型研究土体一维流变固结特性；黄明华等[28]采用分数阶黏弹性模型对洞周超静孔隙水压力消散问题进行求解，但由于未考虑土体压缩性与渗透性在渗流固结过程中的非线性变化，解答的计算精度与适用性受到一定程度的影响.

尽管诸多学者在隧道周围饱和软土固结问题上取得了一定成果，但同时考虑软土压缩性和渗透性非线性变化及土体流变特性影响的研究还不多见.鉴于此，本研究基于渗透系数和有效应力随孔隙比变化的非线性模型，引入分数阶Merchant 模型考虑土体流变特性影响，建立隧道周围饱和软土二维非线性流变固结控制偏微分方程，利用Douglas-Jone 格式的交替隐式差分法对方程进行求解，并在不同隧道渗漏模式、渗透各向异性、初始渗透系数、压缩指数Cc和渗透指数Ck条件下，研究隧道周围饱和软土的非线性流变固结特性.

1 问题描述

隧道周围饱和软土非线性流变固结计算简图如图1 所示.图中，2B为模型宽度，H为深度，均不小于5 倍隧道外直径[29]；r1和r2分别为隧道内、外半径；h为隧道埋深；E0为瞬时加载弹性模量，可以通过试验直接确定；E1和η1为分数阶导数Kelvin 黏弹性体参数；ux、uy为研究区域内点沿x、y方向的位移，vx、vy为该点沿x、y方向的渗流速度.地基表面排水，左右两侧及底部不排水，隧道衬砌均匀渗漏.

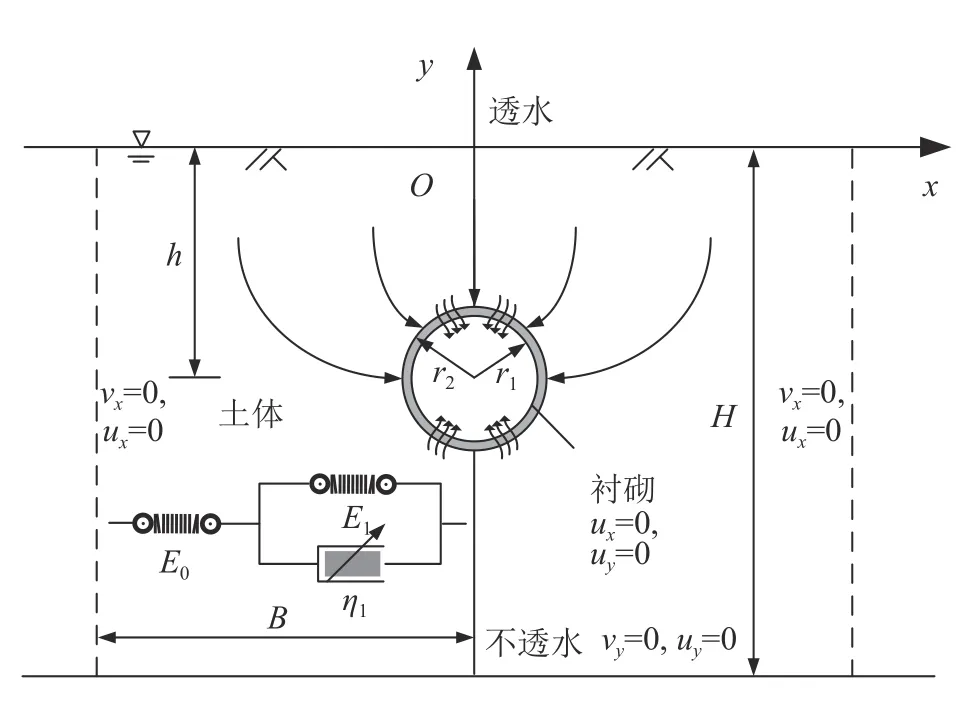
图1 隧道周围饱和软土非线性流变固结计算模型Fig.1 Nonlinear rheological consolidation calculation model for saturated soft soil around tunnels

1.1 基本假定[9]

1) 隧道在纵向上无限长，满足平面应变条件.

2) 土体饱和，土颗粒和孔隙水均不可压缩，孔隙水流动服从Darcy 定律.

3) 土体仅产生小变形.

4) 地基中各点土体所承受的竖向总应力不随时间变化.

5) 地基内各点土体变形自由，不受土体自身或隧道成拱作用带来的影响.

1.2 边界条件

1) 地表完全透水，即纵坐标y=0 时，超静孔隙水压力u=0.

2) 模型左右两侧及底部完全不透水，即当纵坐标y=-H和横坐标x=±B时

3) 土与隧道交界处采用半透水条件(均匀透水)，即当x2+(y+h)2=r22时，

式中：r表示隧道径向坐标，κ 为衬砌与土体的相对渗透性系数，kl和ks分别为隧道衬砌和土体的渗透系数.当 κ=0 时，隧道完全不透水；当 κ 趋向无穷时，隧道完全透水；当 κ 为正的有限值时，隧道处于半透水状态，其透水特性须考虑衬砌与土的渗透系数及衬砌尺寸效应的影响[7].

1.3 初始条件

初始孔压[9]为

式中：u0为盾构掘进完成后的隧道周围初始超静孔压，分布模式与现有文献[30]中保持一致，即盾构机在推入监测地层截面时的分布；ρ 为土体到隧道外表面的距离；

2 控制方程

土单元体内水量变化率等于体积变化率，得到基本控制方程为

式中：γw为水的重度，εv为土体体积应变，t为固结持续时间.

土体压缩性和渗透性服从如下规律[31-32]：

式中：e为孔隙比；e0为初始孔隙比；σ′为有效应力；为初始有效应力，假定沿深度均匀分布(即为常数)；ks0为土体初始渗透系数.

由式(4)、(5)可以得到

小应变条件下黏弹性材料应力应变关系可以表达为

假设总应力 Θ=σx+σy+σz不随时间发生改变，则有

因此，二维情况下体积应变的变化率如下：

式中：μ为土体的泊松比.将式(9)与式(3)、(6)联合可以得到土体二维非线性流变固结控制方程：

式中：rk为土体渗透各向异性系数，定义为水平渗透系数与竖向渗透系数之比.

3 差分方程及求解

有限差分法是一种数值解法，基本思路是将问题定义域进行网格剖分，在网格点上按数值微分公式把定解问题中的微商换成差商，从而把原问题离散化为差分方程，进而得到数值解，在各类偏微分方程求解中得到了广泛应用.对于饱和软土隧道二维固结问题，现有理论解法大多采用保角变换方法，将z平面半无限空间中单一孔洞问题转化为 ζ 平面中的2 个定直径圆环问题，解答仅适用于隧道上部及靠近隧道区域，且适用域形状与径深比有关[5].综上，式(10)采用有限差分法进行求解，差分格式选取Douglas-Jone 格式的交替方向隐式格式，网格划分如图2 所示.图中，x、y方向的空间步长均为0.5 m，时间步长综合考虑计算耗时与精度取0.1 d.隧道圆形边界近似采用八边形网格进行划分，使得网格点与隧道边界点重合.不透水边界条件通过构造虚节点的方法进行处理[34]，半透水边界条件按式(1)进行处理，地表完全透水，超静孔压保持为0.

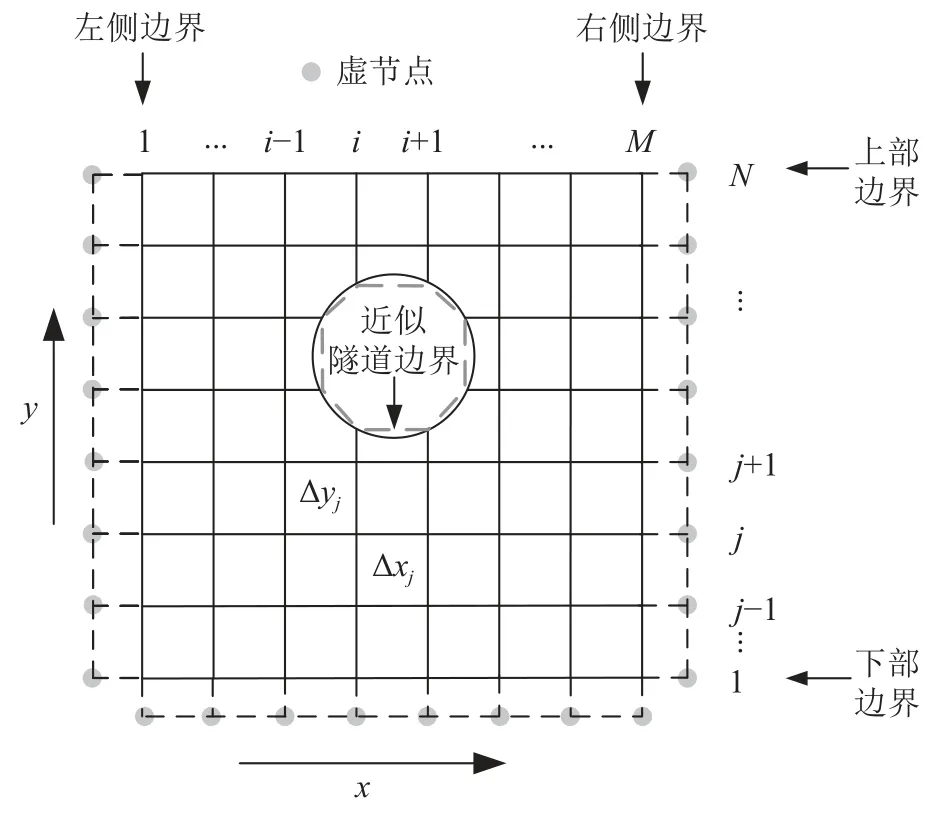
图2 任一时间步下模型网格示意图Fig.2 Schematic of model mesh at each time step

4 验证与分析

为了验证计算结果正确性，将本研究解与现有解析解[9]进行对比，涉及案例为上海地铁1 号线工程，全长为14.6 km，上覆土层厚度为6～8 m，隧道位于软弱的饱和淤泥质黏土层中.在此基础上，研究不同隧道渗漏模式、渗透各向异性、初始渗透系数、压缩指数Cc和渗透指数Ck条件下，隧道周围饱和软土的非线性流变固结特性.

参考上海地区淤泥质黏土三轴蠕变试验数据[35]和软黏土分数阶的阶数取值[33]，分数阶Merchant 模型参数为E0=10 MPa，E1=20 MPa，η1=150 MPa·d，α=0.25.隧道几何参数与物理参数选取见表1，与文献[9]保持一致.表中，γs为土体重度.

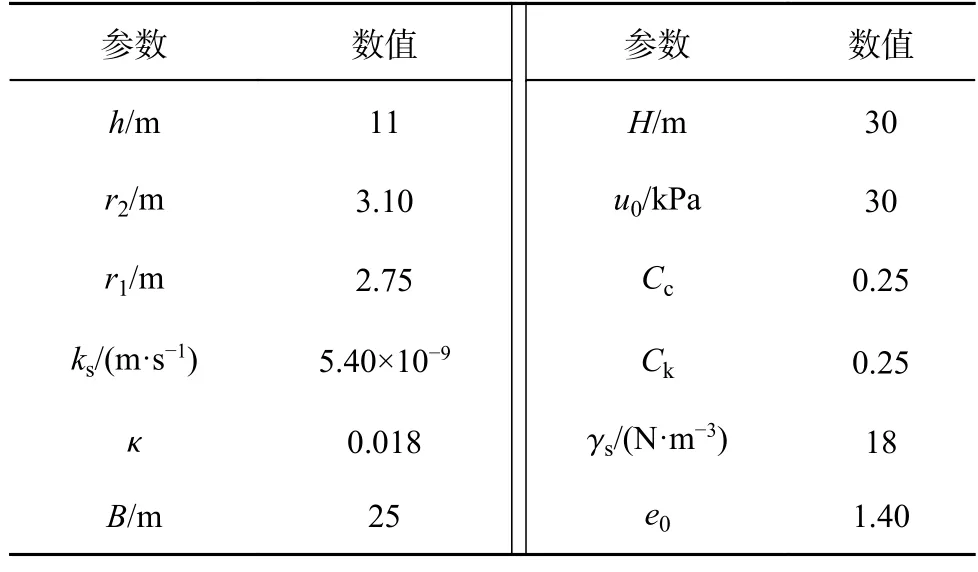
表1 模型几何参数和物理参数Tab.1 Geometric and physical parameters of model

平均固结度按超静孔压定义如下：

式中：si,j=ΔxiΔyj，表示离散点 (xi,yj) 处空间步长所围面积.

4.1 算例验证

如图3 所示为在相同条件下本研究固结控制方程的差分解与基于整数阶Merchant 流变模型的解析解对比.可以看出，本研究方法所得解与现有解析解基本一致.由于2 种解法边界不完全一致，平均固结度发展存在微小差别.

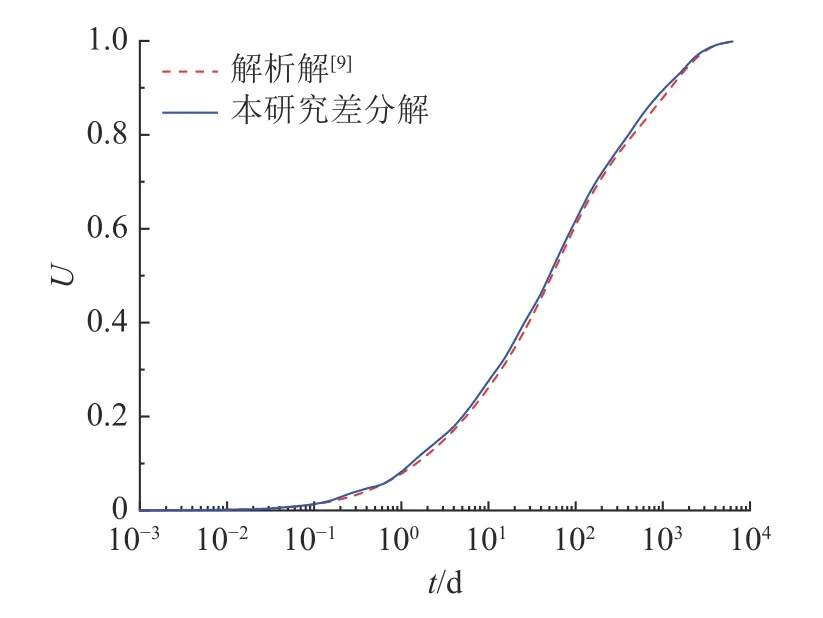
图3 本研究解与已有解析解对比Fig.3 Comparison of solutions of proposed method and existing analytical solutions

4.2 隧道透水模式的影响

盾构管片接头受列车荷载、临近施工和接头自然老化等因素影响，将形成局部透水通道.将盾构局部透水通道简化考虑为沿管片环向分布的6 个完全透水点，其超孔压恒定为0，如图4 所示，研究土体在隧道不同透水模式下的固结性状.

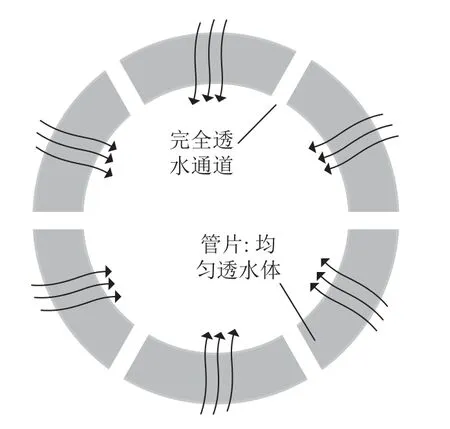
图4 盾构管片渗漏示意图Fig.4 Schematic diagram of shield segment leakage

如图5 所示为隧道作为均匀渗透和均匀渗透-局部渗漏2 种透水边界下，考虑土体流变影响后土体固结速率的对比曲线，其中均匀渗透表示隧道边界处节点孔压服从式(1)所示的半透水条件.可以看出，当隧道为均匀渗透-局部渗漏透水边界时，相同时间内的平均固结度发展更快，这是因为隧道透水通道越多，整体透水能力越强，超静孔压消散越快.此外，无论在哪种渗透边界条件下，在考虑土体本身流变特性时，土体固结速率都将降低，且因考虑土体流变特性而带来的平均固结度差异不随隧道渗漏模式的改变而改变.

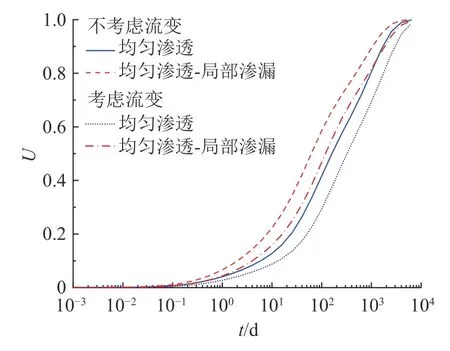
图5 隧道渗漏模式影响下的固结速率对比Fig.5 Comparison of consolidation rates under influence of tunnel leakage modes

4.3 渗透各向异性的影响

滨海软土在自重荷载及长期外部作用下，沉积方向(即竖直方向)的渗透系数一般小于水平方向的[36]，土体表现出渗透各向异性.现有研究表明，考虑渗透各向异性才能准确反映工程的实际情况[37]，胡浩等[36]对杭州原状土进行试验发现渗透各向异性系数rk=1.1～1.4，因此，有必要研究渗透各向异性对隧道周围软土固结性状的影响.

如图6 所示为不同渗透各向异性系数条件下土体固结速率的对比曲线.可以看出，在竖向渗透系数不变的前提下，渗透各向异性的影响较明显，土体固结速率随渗透各向异性系数的增大而增大.此外，对图中相同渗透各向异性系数的曲线进行两两对比还可以发现，渗透各向异性系数的增大不会减小平均固结度差异.

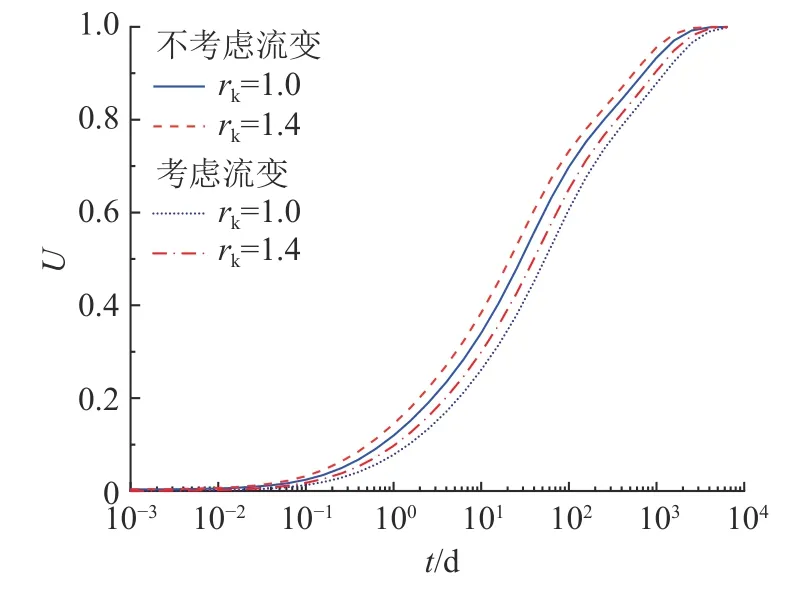
图6 渗透各向异性影响下的固结速率对比Fig.6 Comparison of consolidation rates under influence of permeability anisotropy

4.4 初始渗透系数的影响

如图7 所示为不同初始渗透系数条件下土体固结速率的对比曲线.可以看出，在相同时间内，土体的固结速率随初始渗透系数的增大而增大，而平均固结度差异随渗透系数的增大而减小.当ks0=5.4×10-8m/s 时差值微小，流变的影响可基本忽略，由此可知，渗透系数越大，土体本身流变特性对固结速率的影响越小.

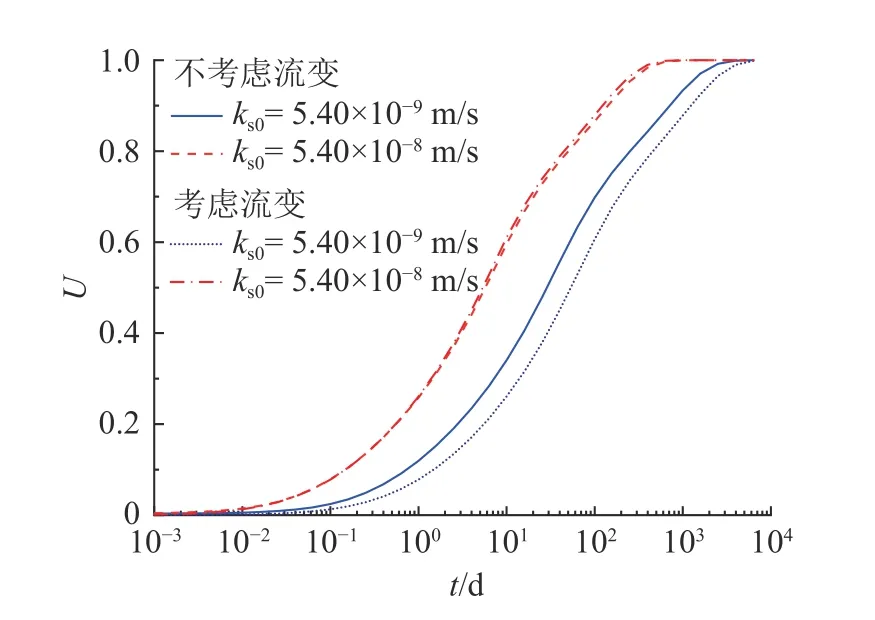
图7 初始渗透系数影响下的固结速率对比Fig.7 Comparison of consolidation rates under influence of permeability coefficient

4.5 渗透指数Ck 的影响

如图8 所示为不同渗透指数Ck条件下土体固结速率的对比曲线.可以看出，渗透指数Ck对平均固结度发展影响较大，当考虑土体流变特性时，平均固结度差异随渗透指数Ck的增大而减小.此外，还可以看出，Ck越大，土体固结速率越小，结合式(6)可知，渗透系数随Ck的增大而减小，从而延缓了土体固结过程的进行，即相同时间内平均固结度随Ck的增大而减小.

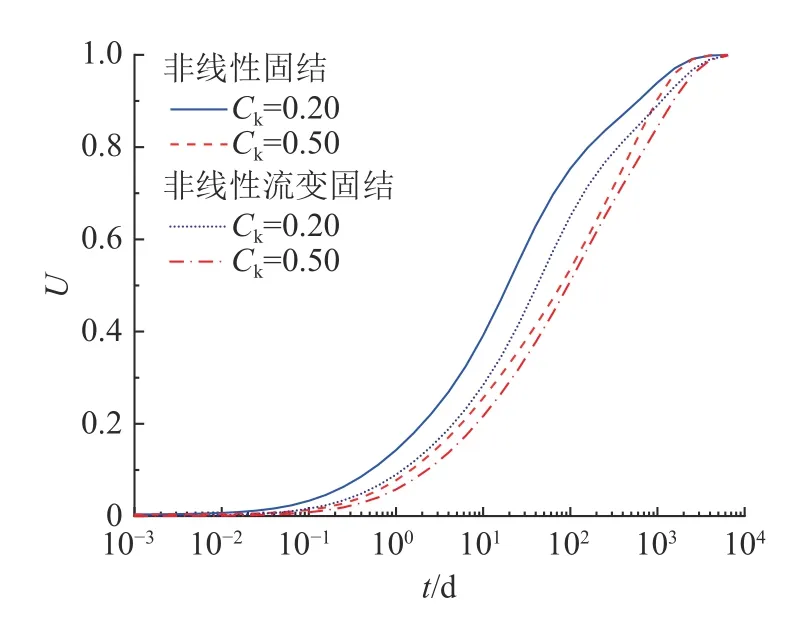
图8 渗透指数影响下的固结速率对比Fig.8 Comparison of consolidation rates under influence of permeability index

4.6 压缩指数Cc 的影响

如图9 所示为不同压缩指数Cc条件下土体固结速率的发展对比曲线.可以看出，压缩指数Cc对固结速率发展影响较小，压缩指数越大，固结速率略微减小；当考虑土体流变特性时，平均固结度差异随压缩指数的增大而略微增大.此外，与图8 进行对比后还可以发现，渗透指数Ck对土体固结速率的影响比压缩指数Cc的影响更为显著.

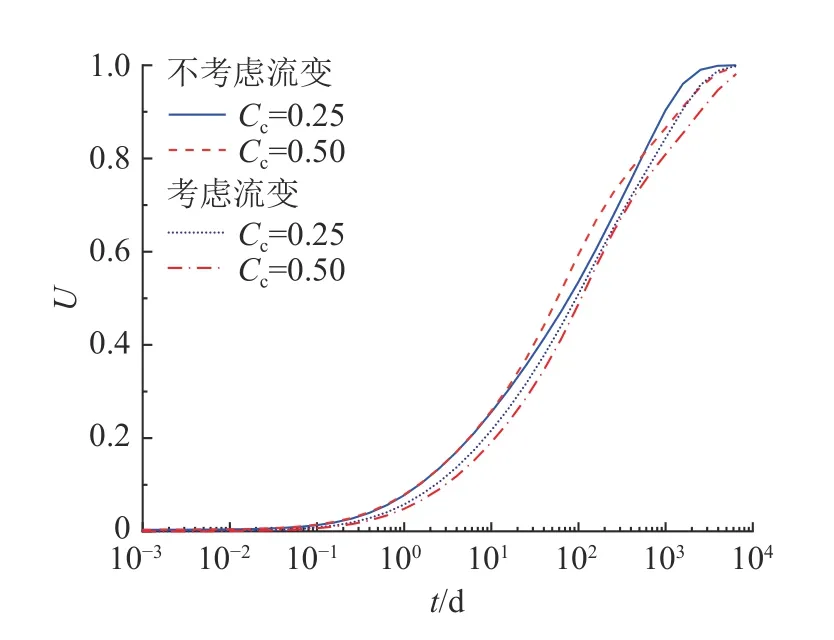
图9 压缩指数影响下的固结速率对比Fig.9 Comparison of consolidation rates under influence of compression index

5 结论

（1）土体流变特性的存在会显著降低土层的固结速率，但当初始渗透系数增大到一定程度时，土体流变特性对土层固结速率的影响可以忽略.

（2）隧道渗漏模式对土体固结速率影响较大，隧道的局部渗漏会增加透水通道，导致土体固结速率加快.

（3）渗透各向异性系数对固结速率有较大影响，在进行固结性状分析时，应当充分考虑土体不同方向渗透系数的差异.

（4）初始渗透系数对土体固结速率影响较大，初始渗透系数越大，土体固结速率越快.

（5）渗透指数Ck对土体固结速率影响较大，压缩指数Cc影响相对较小.当Ck或Cc增大时，土体的固结速率会减小.

（6）本研究中假设地基为单层地基，与实际工程情况略有不同.为了增强计算理论的适用性，可进一步研究多层地基情况下施工扰动引起的隧道周围土体固结特性.