融合ER和分层BRB的CPU性能分析模型

陈伟伟,曲媛媛,贺 维,3 ,朱海龙,张广玲,魏洪伟

1(哈尔滨师范大学 计算机科学与信息工程学院,哈尔滨 150500) 2(黑龙江农业工程职业学院,哈尔滨 150503) 3(火箭军工程大学,西安 710025)

1 引 言

CPU的性能分析是CPU设计的一个重要参考目标,也是衡量CPU设计水平的一个基本指标[1].随着CPU性能不断的提升,处理器设计与制造也更加精密复杂,这也要求CPU的性能分析达到更加准确、可靠的要求.通过对影响CPU的观测指标进行评估并综合分析得到性能的预测结果,能够提高性能分析的准确度,为处理器的设计提供更加可靠的参考.

在处理器性能分析和建模方面,根据处理器结构参数的获取方式可以将建模方法分为机械建模和经验建模两大类,其中机械建模以CPU的结构特征为基础,研究CPU结构中影响性能的各部分因子,并整合得到衡量处理器性能的公式,其中公式中的结构参数及相关的参数由模拟器进行简单快速测量获取[2].例如Hartstein[3]等人建立的顺序、乱序超标量处理器的分析模型,优化了CPU的前端流水线深度,但需要使用模拟器获得模型的一些输入参数.不同于机械建模,经验建模不需要对CPU的内部结构详细认知,采用一些通用的函数或方程为基础,将模拟器对CPU构建的参数进行模型训练,不断优化模型获得合理的误差,同时训练后的模型能够用于新型处理器结构性能的预测.Vijay[4]等人利用人工神经网络ANN模型,将一些处理器性能特征输入到3种不同神经网络架构模型中,经过权重调整得到的结果比线性回归方法更好.根据性能预测的技术方法可以将建模方法划分为基于时间序列技术建模和基于多种非线性模型混合建模两类[5].早期性能预测主要使用时间序列技术,例如,Valenzuela[6]等人提出了一种将线性时间序列、人工神经网络和遗传算法相结合的混合预测模型.随着非线性模型被广泛用于产生更精确的预测结果,应用于不同方向的混合驱动模型不断提出.Kholidy[7]提出了一种群体智能的方法,用于预测CPU利用率、内存利用率、响应时间和吞吐量,它将多个支持向量回归模型和自回归综合移动平均模型相结合进行预测,并采用粒子群优化算法来选择这两个模型的最佳特征和估计参数.Rahmanian等人[8]考虑预测虚拟机CPU的使用量问题,提出了一种基于学习自动机理论的集成预测算法,它包括多个预测模型和学习自动机来调整这些模型的权重.Cao[9]等人研究了一种支持CPU负载预测的动态集成预测模型,它由两层组成,一层是预测优化层,用于生成新的预测值,另一层是预测集成层,用于组合预测结果.以上方法分别从结构和技术角度分析了CPU性能的建模过程,然而考虑到CPU复杂的设计流程,测量的参数指标往往复杂多类,基于非线性的混合驱动模型虽然能够构建性能分析模型,但多指标信息增加了模型复杂度,导致计算时间长、计算量大、效率低.另一方面,以神经网络(Neural networks,NN)为代表的黑盒模型的内部参数和结构难以为人所理解,分析结果的合理性和可靠性也难以得到验证,给实际工程应用带来了潜在的风险[10].为了实现系统的高可靠性需求,需要从可解释性角度出发,通过合理的建模方法构建出可靠且可理解的模型来增强人们对实际系统的认知,获得系统真实状态[11],从而对系统进行更好的设计和改进.总之,目前的CPU性能建模方法并未充分考虑指标数据的多样性,且无法很好的解释分析过程,对处理器结构不具有洞察性.

针对CPU性能分析中出现的分析指标复杂、分析过程不具有可解释性的问题,可以采用证据推理(evidence reasoning,ER)算法来进行指标评估,同时构建置信规则库(Belief Rule Base,BRB)对CPU性能进行综合分析.证据推理[12]作为一种可解释性的推理方法,从评估的角度出发,利用Dempster规则对证据进行组合,降低指标复杂度,实现不确定性推理.通过ER算法对影响处理器性能的因素指标进行梳理,能够给出可靠的评估结果,为处理器性能的综合分析提供依据.BRB作为一种由If-Then规则、传统D-S理论扩充发展起来的专家系统[13],它最早由英国曼彻斯特大学Yang提出.BRB使用ER进行知识推导,能够建立输入与输出复杂的非线性关系[14].目前,已被广泛应用于健康状态评估、网络安全状况感知、故障诊断、医学决策等领域[15].采用BRB构建CPU性能分析模型时,首先结合ER评估结果与专家知识作为输入参数,转换为if-then规则的表达形式,然后采用ER算法进行规则汇总,最后得到性能分析的结果.因此,BRB在综合分析过程中能够清晰的解释推理过程,使得分析结果具有可追溯性.

考虑到BRB在面对多指标复杂系统建模时容易产生组合规则爆炸,影响模型的评估结果.采用分层BRB能够避免这一问题[16].分层BRB采用相对较少的规则建立了层次化的结构模型,首先对底层指标进行组合,之后将上一层结果作为下一层的输入,不断组合直至目标输出状态[17].这种层次结构合理易理解,同时保证了CPU性能分析过程的可解释性.

综上,本文提出一种融合ER和分层BRB的CPU性能分析模型,首先采用ER对分类指标进行评估,降低系统复杂度.然后将评估结果作为分层BRB模型的输入,通过分层BRB构建多指标CPU性能分析模型,最后基于优化算法构建优化模型,调整模型的初始参数,进一步提高模型的准确率.

本文的组织结构如下,第2节阐述了CPU性能分析过程中需要解决的3个问题,第3部分阐述了融合ER和分层BRB构建的CPU性能分析模型,同时结合鲸鱼算法定义了优化模型.第4部分结合具体的案例分析验证了模型的有效性,最后总结了模型的结构与步骤,并探讨了未来的工作与展望.

2 问题描述

可靠的性能分析方法对于CPU的设计具有重要参考意义,传统的性能分析模型无法较好的应对输入的复杂指标参数,处理器结构越复杂,模型的准确度越低,同时模型内部结构不易理解,输出过程无法推导证明.因此,构建合理且准确的性能分析模型能够有效提高在实际应用中的CPU性能分析的可靠性.本节阐述了CPU性能分析过程中存在的问题,并提出了一种融合ER和分层RBR的CPU性能分析模型.本文主要解决以下3个问题:

问题1.在实际应用中,影响CPU性能的指标类型多且关系复杂,需要从不同层面对CPU性能指标进行分析.通过从多层面构建指标评估模型能够有效降低指标复杂度,为性能分析提供依据.如何采用ER算法构建指标评估模型成为第一个需要解决的问题,如式(1)所示:

x′i=ER(x1,x2,…,xi,α,λ)

(1)

其中,x′i表示CPU性能指标的评估值,xi表示输入属性,α表示模型参数向量,λ是构建模型中的专家知识,ER(·)表示融合函数.

问题2.在CPU性能分析过程中,模型的可解释性是系统建模的重要参考因素,传统性能分析过程不具有可解释性且输出结果不可追溯,BRB作为一种知识推导模型,能够描述、转换和整合输入的不确定信息并得到统一结果,同时保证推理过程的可解释性.如何建立合适的分层BRB模型进行CPU性能分析是第2个需要考虑的问题,推理过程如式(2)所示:

yt=HBRB(x′1,…,x′k,U′)

(2)

其中yt表示未进行优化的分层BRB性能分析的结果,x′k代表上一层子BRB的结果,U′表示分层BRB系统中的参数集,HBRB(·)为最后一层BRB的融合函数.

问题3.在实际性能预测过程中,初始分层BRB模型中的专家知识具有局限性[18],如何结合优化算法,构建优化模型以提高模型精度是第3个需要解决的问题,优化推导过程可以描述为式(3):

U′=Optimize(HBRB(·),υ)

(3)

其中,Optimize(·)代表分层BRB的优化函数,ν是优化前的参数集,U′表示优化后的结果集.

3 构建CPU性能分析模型

本节从原理推导的角度阐述了如何完整的构建CPU性能分析模型,主要包括:1)CPU性能分析实现过程;2)基于ER的CPU指标评估模型;3)基于分层BRB的性能分析模型.

3.1 CPU性能分析实现过程

处理器的硬件结构作为CPU设计的主要技术目标,对性能的分析具有重要的参考性.本文以CPU硬件指标为目标,构建模型整体结构,性能分析模型由3个组成部分,如图1所示.

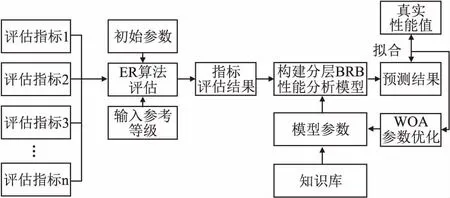
图1 CPU性能综合分析流程图Fig.1 Flow chart of comprehensive analysis of CPU performance

1)指标评估.作为一种智能决策方法,ER首先将输入信息进行数据预处理,然后输入到构建的模型评估,可以有效的降低输入指标的复杂度,同时这种评估充分考虑了指标间的实际关联,保证了评估结果的可解释性.

2)性能分析.传统BRB面对多指标复杂系统的决策问题时容易产生组合规则爆炸,影响模型的准确度.分层BRB采用层次结构对输入指标进行组合,结果作为下一层的输入,有效减少了规则的数量,简化模型的计算复杂度.

3)参数优化.通过WOA构建优化模型,提高模型的精度.

3.2 基于ER的CPU指标评估模型

对于一些复杂结构的处理器,在实际模拟器构建参数的过程中,因为延时误差,某些指标数据可能产生数据缺失.指标种类复杂以及数据获取的难度给处理器的性能分析带来很大影响.另一方面,根据指标的机理分析,影响处理器性能的指标之间可能存在相关性,在进行性能评估时,如果单独对每个指标进行分析,分析过程孤立且结论缺乏说服力,而盲目筛选指标会造成信息损失,评估结果存在误差.因此,本文采用ER算法构建CPU指标评估模型.CPU性能指标评估流程如图2所示,主要实现步骤如下:

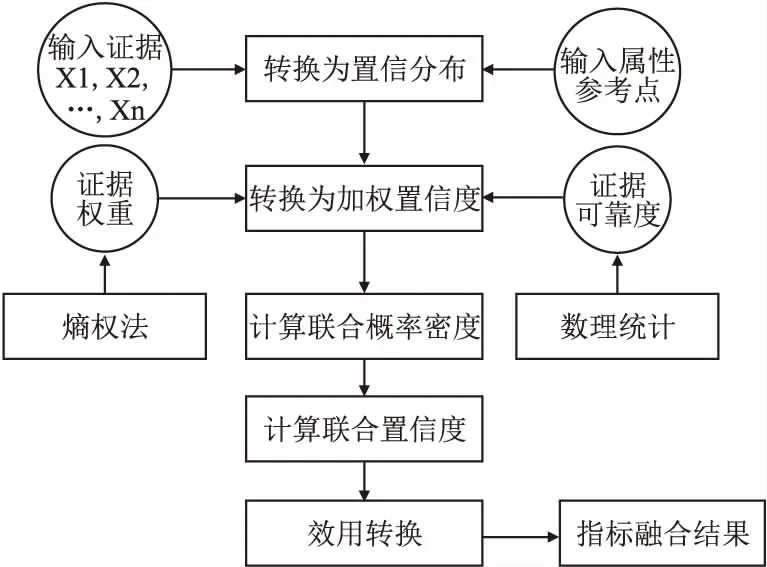
图2 CPU性能指标评估流程图Fig.2 Flow chart of CPU performance index evaluation

步骤1.根据专家知识初始化指标中不同评估等级的置信度,第i个指标可以描述为:

ei={(βr,σr,i),(θ,σθ,i),r=1…R,i=1…N}

(4)

其中βr表示第r个指标数据的评估级别,σr,i表示在证据ei下被评估为等级βr的置信度.θ表示全局无知,σθ,i表示第i个指标中数据未分配的置信度.

步骤2.计算证据ei基本概率质量,如式(5)～式(7)描述:

mr,i=1-ωiσr,i

(5)

(6)

mε,i=1-ωi

(7)

其中,mr,i表示的是第r个指标中第i个指标等级的基本概率质量,mδ,i代表未分配给数据等级集合的基本概率质量,mε,i为缺少的第i个数据指标概率质量.

步骤3.基于Dempster规则求解组合概率质量:

mr,J(i+1)=FJ(i+1)[mr,J(i)mr,i+1+mr,J(i)mθ,i+1+mθ,J(i)mr,i+1]

(8)

mθ,J(i)=mθ,J(i)+mu,J(i)

(9)

mu,J(i+1)=FJ(i+1)[mu,J(i)mu,i+1+mu,J(i)mθ,i+1+mθ,J(i)mu,i+1]

(10)

mL(Θ),J(i+1)=FJ(i+1)[mθ,J(i)mθ,i+1]

(11)

(12)

步骤4.根据上述结果计算联合置信度:

(13)

步骤5.假设评估等级βr的效用为u(βr),那么评估的期望效用计算如下:

(14)

基于上述分析,式(14)的结果作为离散型随机变量的数学期望,能对影响处理器性能指标进行有效的评估,按照参考等级可以将效用值的分布划分为由低到高的优差程度,某类指标的效用值越高,代表该类属性对处理器的性能影响越大,验证了CPU性能评估方案的有效性.

3.3 基于分层BRB的CPU性能分析

本节定义了基于分层BRB的CPU性能分析模型及其推理过程,主要包括:

1)阐述分层BRB的推理过程;2)给出分层BRB的CPU性能分析模型的基本结构;3)建立基于WOA的分层BRB参数优化模型,并给出优化步骤.

3.3.1 分层BRB的推理过程

BRB是一种以ER算法为推理引擎的专家系统,它能将性能指标中不确定性信息转换为置信分布形式的if-then规则,同时结合专家给定的经验知识共同组成置信规则库[19].BRB对于不确定信息具有很强的表达转换能力,但输入属性过多时,容易造成规则组合爆炸问题.分层BRB系统由若干个子BRB组成的,每个子BRB都能对输入属性的信息转化为规则,将指数增长的规则数量降低到常数级,有效避免了组合爆炸.每条规则的基本结构如下:

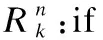
(15)

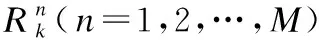
模型推理过程如图3所示,具体推理步骤如下:

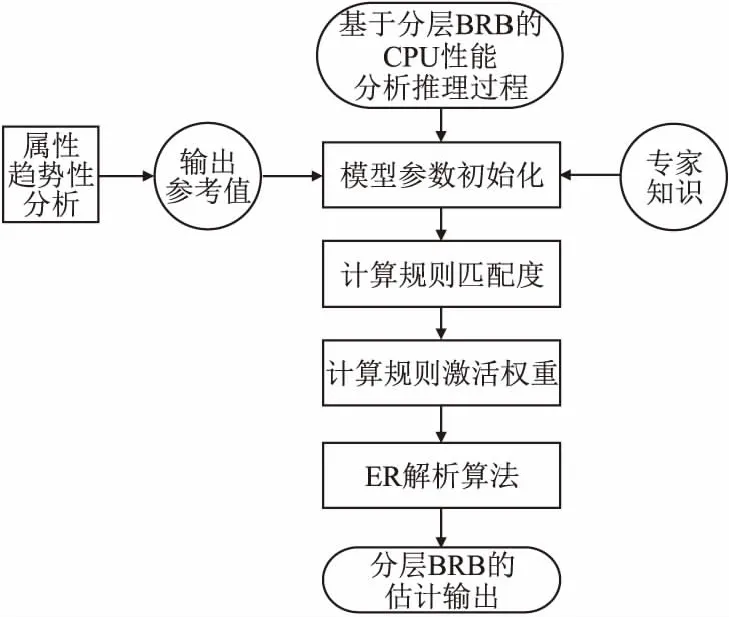
图3 分层BRB模型推理流程图Fig.3 Inference flow chart of hierarchical BRB model

步骤1.初始化规则的置信度,分层BRB的参数集合可以按式(16)描述:

ρn={λ1,…λk,μ1,1…μR,K}

(16)

步骤2.如式(17)计算输入值与参考值的匹配度:

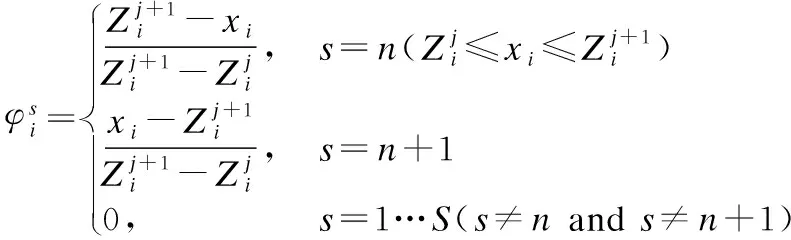
(17)

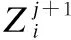
步骤3.计算规则的激活权重,权重计算公式描述如(18)所示:

(18)

其中,Wk是第k条置信规则的激活权重,θk代表第k条规则的权重,δi代表属性权重,T表示先行属性的数量.

步骤4.基于ER解析算法计算性能指标评估结果的置信度,过程描述如式(19)、式(20)所示:

(19)

(20)

其中,βn是模型产生的第n条评估等级置信度.

步骤5.按照效用公式计算输出结果为式(21):

(21)

其中,yt表是模型的实际输出,βr表示相对于评价结果Dr的置信度.

3.3.2 分层BRB的CPU性能分析模型基本结构

本节针对性能分析模型的基本结构进行推导,主要分为以下4个步骤,分层BRB模型的基本结构如图4所示.

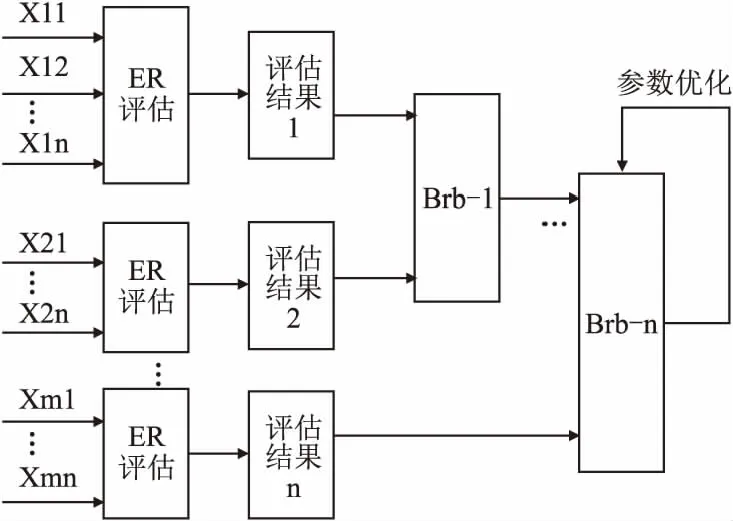
图4 分层BRB模型的基本结构图Fig.4 Basic structure of the hierarchical BRB model

步骤1.总结影响处理器性能的硬件指标参数,按照种类可描述为F={(X11,X12,…,Xij)|1≤i≤m,1≤j≤n},m代表类别数,n代表每种类别参考指标的数目.

步骤2.通过ER底层评估分类指标后,得到CPU性能评估结果,作为子BRB的输入激活规则,Resultn=Evaluate(x1,x2,…,xi,f,λ),Resultn代表指标融合后的性能评估结果,也作为BRB1的输入.

步骤3.将子BRB模型的结果Inputn用作下一层子BRB-1的输入,结合专家知识给出下一层BRB的输出,这样通过ER方法逐层推理子BRB可以生成分层BRB-n的结果.分层BRB的估计输出可按式(21)表示.

步骤4.结合优化算法对分层BRB的最后一层进行优化,通过模型负反馈训练调整专家知识和参考值,得到优化后的评估结果,可表示为Output′=Optimize(yt,output).

Remark:构建分层BRB的一个关键目标是描述属性与结果之间的关系,这涉及到中间变量的解释[17].属性与结果之间的关系可以通过模型结构和参数来描述并解释.参数可以参考趋势性分析进行描述,而单层BRB模型结构本身是由专家知识及历史数据确定的规则组成,因此,将历史数据进行趋势性分析并结合专家知识能够得到分层BRB的结果参考值[20].

3.3.3 基于WOA的分层BRB的参数优化过程

初始分层BRB性能分析模型的参数是由专家结合经验知识给定的,考虑到处理器复杂的设计机理,未经训练的模型具有一定的局限性.为提高分层BRB性能分析模型的准确性,需要结合优化算法构建训练模型,优化输出的结果.参数优化的具体步骤如下:

步骤1.首先将待优化参数分别输入到实际系统和置信规则库中训练,得到实际输出值yi和估计输出值yt.

步骤2.根据实际系统得到的专家知识以及训练模型输出的均方差给出优化目标函数:

(22)

优化目标和约束条件可以表示为:

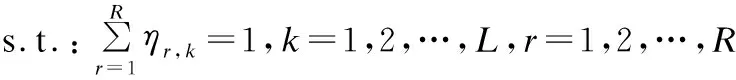
(23)

步骤3.采用鲸鱼优化算法,以式(23)作为优化约束条件,MSE最小值作为优化目标.

鲸鱼优化算法(whale optimization algorithm,WOA)是由MIRIALILI提出的一种模拟座头鲸捕食猎物行为的新型智能优化算法[21].该算法将猎物的位置抽象为一个对应的最优解,鲸鱼通过种群个体搜索,收缩包围猎物来实现最终到达猎物位置即最优解位置.由于鲸鱼算法原理简单,参数设置少和具有较强的全局搜索能力的优点,目前已经广泛应用于风电功率预测[22],无线传感器网络覆盖优化[23]等.优化算法实现流程图如图5,具体步骤按如下:

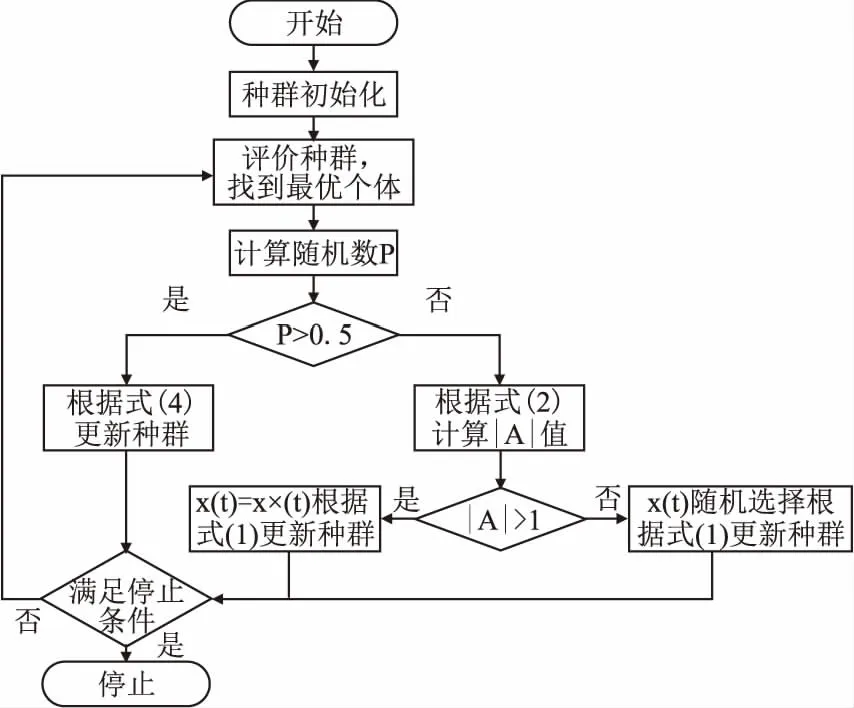
图5 鲸鱼优化算法流程图Fig.5 Flowchart of whale optimization algorithm

种群的初始化:由于初始时鲸鱼的位置随机,且对猎物位置没有先验知识,假定当前个体为最优个体位置,鲸鱼种群向当前最优个体包围,鲸鱼个体如式(24)更新自身位置:

X(t+1)=X′(t)-A|C×X′(t)-X(t)|
A=2ar-a
C=2r

(24)

其中,t表示当前迭代次数,A和C为系数向量,X′(t)代表当前最优个体的位置向量,X(t)表示当前要更新的个体的位置,X(t+1)为个体更新后的位置,r为[0,1]间随机数,缩放因子a在迭代过程从2线性减小到0.

鲸鱼在捕杀猎物阶段时,存在50%的概率在螺旋模式和缩小环绕机制之间选择[24],以更新自身位置.当|A|≤1时,鲸群在最优个体的带领下向猎物收缩,当|A|>1时,鲸群在随机个体带领下搜索猎物,式(24)中的最优个体位置由任一个体的位置代替,整个狩猎过程中,鲸鱼个体更新自身位置如式(25)、式(26)所示:

(25)

(26)

其中,p为[0,1]间随机数,当p>0.5时,鲸群采用螺旋模式捕食猎物,X*(t)为当前状态下最优个体的位置,b为常数,l通常随机取值[-1,1],为控制螺旋形状的参数.X′(t)为种群中任一个体位置.根据p的取值,鲸群能在螺旋或环绕机制之间选择,最后通过满足一个终止准则来结束优化算法.

4 案例研究

4.1 数据说明

本文以一项来自UCI计算机硬件数据集进行实验,验证模型的有效性.该数据集样本总数为209,共7个属性,影响处理器性能主要因素的参数说明如表1所示.

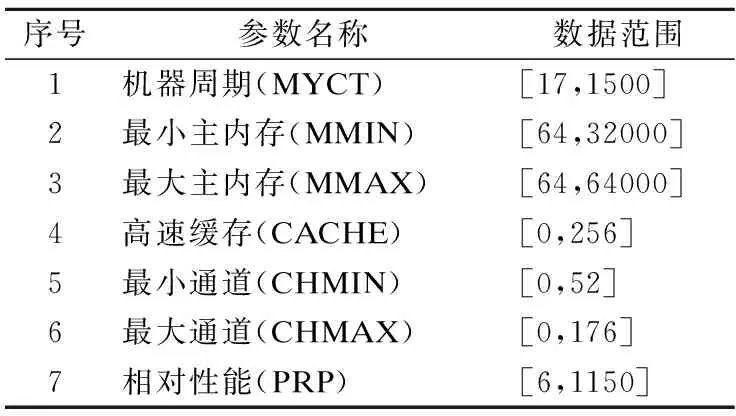
表1 参数说明Table 1 Parameter description

根据原始数据集绘制预测指标趋势变化图6,预测指标对相对性能变化影响总结如表2,可以得到主存数、高速缓存、通道数与相对性能值呈正相关,而机器周期与相对性能值呈负相关.与实际情况对比,机器周期时间越短,说明处理器完成一个基本操作时间越短,单位时间内能完成更多的操作,性能也就越好.而CPU的缓存容量(包含cache)越大,数据的处理速度越大,处理器运行速度也更快.通道数越多,能并行执行的程序也越多,处理器的相对性能也更强.因此,预测指标的变化趋势分析具有实际意义,是可靠的.

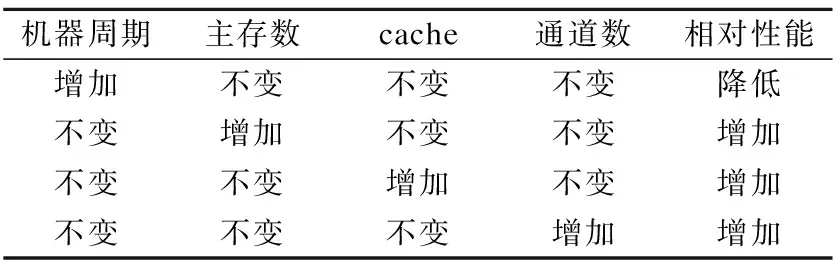
表2 预测指标对相对性能的影响总结Table 2 Summary of impact of predictors on relative performance

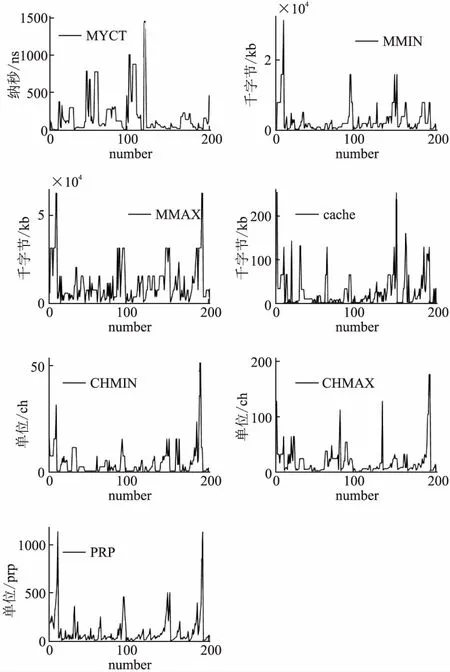
图6 预测指标趋势变化图Fig.6 Trend chart of forecast indicators

4.2 性能分析流程

本节以计算机硬件数据集为案例,给出性能分析的流程.首先,构建融合ER和分层BRB的CPU性能分析模型进行训练,然后结合WOA改进分层BRB模型,最后,结合试验结果进行分析总结.

4.2.1 CPU性能分析模型的构建

通过数据的趋势性分析,可以总结影响CPU性能的因素分为存储、机器周期、通道3类,其中存储包含MMIN,MMAX,CACHE,通道包含CHMIN和CHMAX.考虑到每种因素包含多个指标,为了保证评估结果的可靠性,采用证据推理算法对分类指标进行评估,得到的效用值可以用来评价该类因素的影响程度.假设St、Mt、Ct分别代表存储效用值,机器周期效用值和通道效用值.ER算法评估指标的参数设置如表3、表4所示.

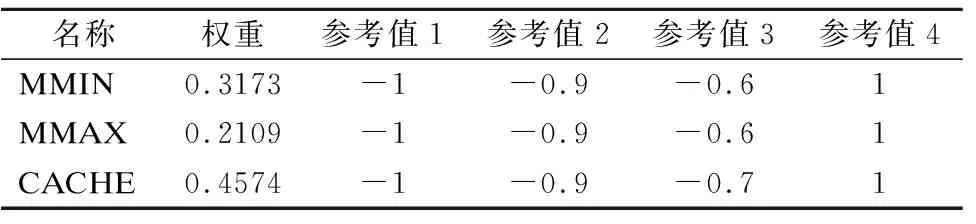
表3 存储评估参数设置Table 3 Store evaluation parameter settings

表4 通道评估参数设置Table 4 Channel evaluation parameter settings

各因素指标评估后,效用值作为子BRB的输入参数,为了避免输入属性过多出现规则组合爆炸问题,构建分层BRB性能分析模型,模型结构图如图7所示,首先,将存储St和通道Ct作为子BRB1的输入,结合专家知识构建初始置信规则库及输出参考值,然后,BRB-1的输出Pt与性能影响因素机器周期Mt共同作为BRB-2的输入参数,最后,完成模型的训练并得到预测结果.

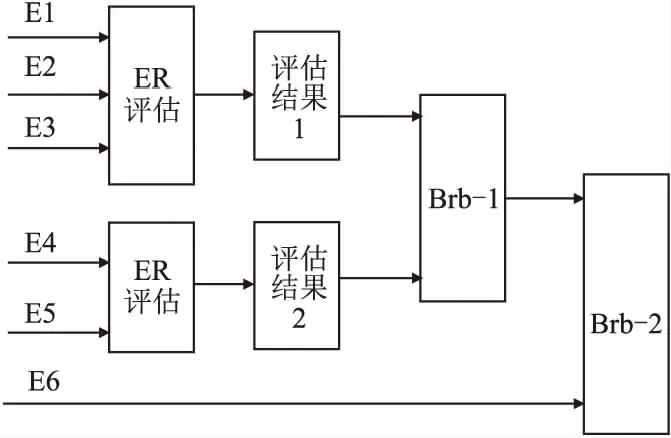
图7 融合ER和分层BRB性能分析模型结构图Fig.7 Structure diagram of the performance analysis model based on ER and hierarchical BRB

以BRB-1为例,输入属性St、Ct对应的置信规则表达为式(27):

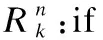
(27)

分层模型共有2层2个子规则库,子规则库1和2分别有25条规则,模型的初始参数由专家给出,对输入指标设置5个参考等级,非常小(very small,VS),小(small,S)、中(median,M)、大(large,L)、非常大(very large,VL),处理器的相对性能也设置4个参考等级小、中、大、非常大.BRB-1和BRB-2的指标参考等级和参考值如表5、表6所示:

表5 BRB-1中的指标参考等级和参考值Table 5 Indicator reference level and reference value in BRB-1

表6 BRB-2中的指标参考等级和参考值Table 6 Index reference level and reference value in BRB-2

在初始分层BRB模型中,专家知识具有局限性,从而影响了模型的准确性.为解决参数的优化问题,基于WOA进行参数优化,迭代训练次数为800,优化维度为82,种群大小为25,训练集包含209例数据,测试集100条数据,以BRB-2的初始参数为例,优化后参数如表7所示.

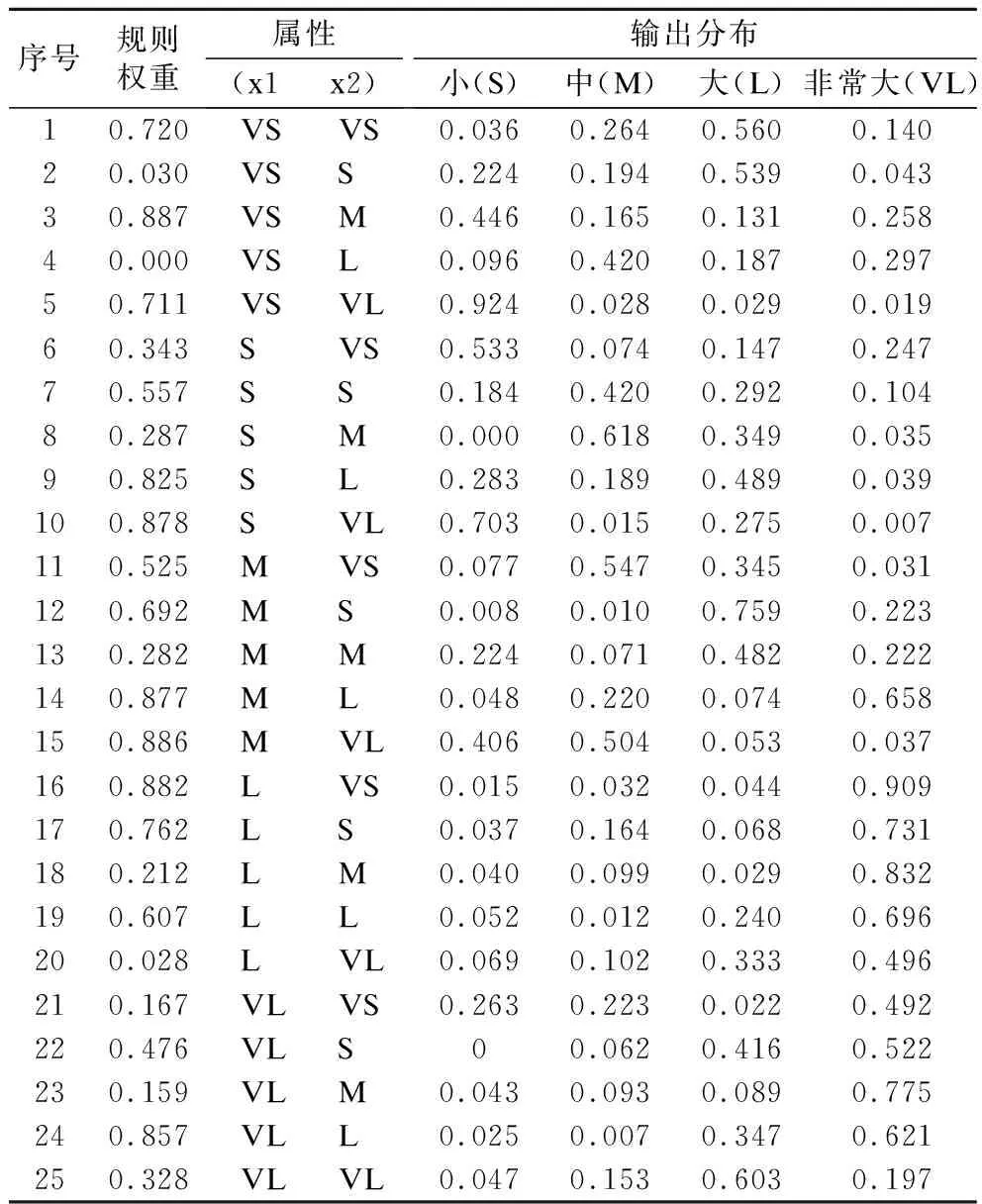
表7 BRB-2优化后的置信度Table 7 Confidence after BRB-2 optimization

4.2.2 模型仿真分析

为清晰的理解融合ER和分层BRB模型CPU性能分析的具体流程,选取了任意两条数据用于ER指标评估和BRB模型训练.具体分析过程如下:

步骤1.首先采用ER算法将不同指标转化为不同评估等级的置信度,然后根据公式计算期望效用值,评估指标的性能状态.

归一化处理后,某处理器最小主内存、最大主内存、cache表示为(-0.988,-0.814,1),权重分别为(0.3173,0.2109,0.4574),其置信度可表示为:

e1={(-1,0.88),(-0.9,0.12),(-0.6,0),(1,0),(Θ,0)}
e2={(-1,0),(-0.9,0.714),(-0.6,0.286),(1,0),(Θ,0)}
e3={(-1,0),(-0.9,0),(-0.6,0),(1,1),(Θ,0)}

然后根据公式(5)～公式(13)计算出存储类指标的联合概率密度,表示为:

e1-3={(S,0.30),(M,0.32),(L,0.08),(VL,0.30),(Θ,0)}

e1-3代表存储因素对性能的影响分布,继续按式(14)效用计算得到存储效用值x1′=4.77.同理按照上述步骤对通道类指标进行评估,得到通道类指标联合概率密度为:

e1-3={(S,0),(M,0),(L,0.86),(VL,0.14),(Θ,0)}

通道效用值为:x2′=6.747.

步骤2.将上述存储效用评估值与通道效用评估结果作为输入规则,代入分层BRB-1模型,计算得到第1层BRB的输出结果.

依据式(16)、式(17)计算两条输入规则与参考值的匹配度:

然后根据公式(18)计算激活规则的激活权重:

ω1=0.00713ω2=0.00957
ω3=0.4199ω4=0.5634

最后结合优化算法对参数进行优化,计算输出结果yt=-0.6462

步骤3.BRB-1的输出值与机器周期指标作为输入代入BRB-2进行最后优化,计算过程重复步骤2中的计算公式,得到最终的性能预测值yt=-0.65,真实相对性能值为yactual=-0.66.

通过对上述实际数据的分析,可以得到误差较小的相对性能预测值.一方面说明了本文所提模型的有效性,另一方面也证明了模型推理过程清晰透明,输出结果可追溯,建模过程具有可解释.

4.3 实验分析与对比实验

在本节中,如图8所示,预测值与真实值拟合效果较好,基于WOA优化后的分层BRB模型能够较为准确的预测处理器的相对性能.同时,为验证模型的有效性,将本文方法与反向传播神经网络(BPNN)、极限学习机(ELM)、径向基函数神经网络(RBFNN)、随机深林(RF)4类机器学习方法对比,训练与测试的数量相同,分别进行10轮实验,实验结果如表8所示,该模型的平均MSE为0.0026,准确率最高,反映本文所提模型的有效性与准确性.

考虑到4种方法的参数设置对实验结果的影响,采用控制变量法对每种机器学习方法的参数设置进行实验,计算实验结果的区间范围,如表9所示,4种方法的较优参数设置如表10～表13所示.本文研究的ER和分层BRB模型虽然存在一定的误差,但误差值在0.002-0.0035之间,与其他方法对比误差值变化比较稳定.

表9 不同参数设置实验结果统计表Table 9 Statistical table of experimental results with different parameter settings

表10 BPNN神经网络初始参数Table 10 BP neural network initial parameters

表11 ELM初始参数Table 11 ELM initial parameters

表12 RBFNN初始参数Table 12 RBFNN initial parameters

表13 RF初始参数Table 13 RF initial parameters

为了更好的对本文模型进行评估,选取了所提算法中优化BRB过程的伪代码,如表14所示,分别从时间复杂度、空间复杂度两个角度分析.

表14 优化BRB伪代码Table 14 Pseudocode for optimizing BRB

1)时间复杂度:通过大O描述算法的运行时间与输入数据之间的关系,可以从评估算法的执行效率.在BRB优化之前,需要对第一批搜索代理进行初始化,遍历不同维度,产生范围内的随机数,大小表示为O(dim*Boundary_no),然后遍历置信规则中的参考值,依次进行训练计算.该过程的复杂度可表示为O(L*N),因此,采用乘法法则,整个优化过程的时间复杂度O(L*N*(dim*Boundary_no)),其中,L,N,dim,通常为常量.

2)空间复杂度:采用大O来描述算法的存储空间随着数据规模变化的趋势,使得空间复杂度的分析变得容易.在初始化搜索代理阶段,需要申请的空间变量包括Boundary_no,dim,ub_i,lb_i,其中,dim为常量阶,和数据规模n没有关系,Boundary_no为二位数组,ub_i,lb_i为一维数组,因此,根据加法法则,该过程的空间复杂度可计算为:O(Boundary_no+ub_i+lb_i)≈O(n2),然后遍历阶段申请空间变量包括L,M,BeliefF,其中L,M为常量,表示为O(BeliefF),优化过程的空间复杂度可表示为:O (n2+BeliefF)=O(n2).

为了比较优化模型实验效果,如表15所示,统计了6轮初始模型和经WOA优化后模型的MSE值,例第3轮实验中,初始模型MSE为0.0687,WOA优化后模型MSE为0.0025,相比于初始模型精度提升了一倍,优化前后拟合结果如图9所示.

表15 优化前后模型MSE对比Table 15 Model MSE comparison before and after optimization

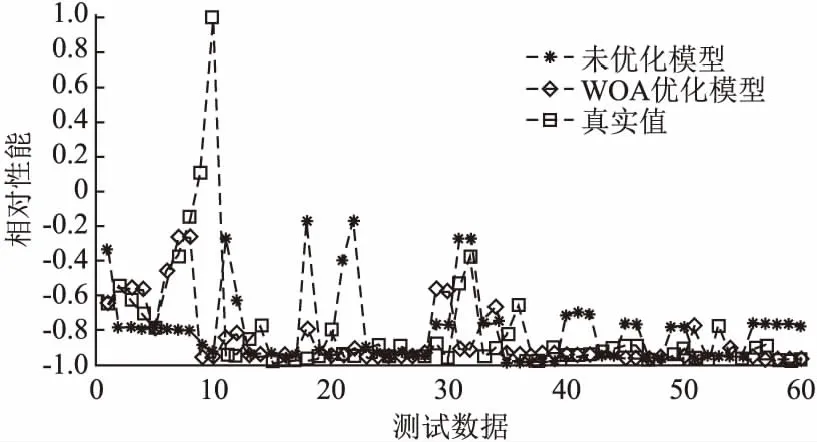
图9 未优化&优化模型预测值与真实值拟合图Fig 9 Fitting graph of predicted value and true value of unoptimized and optimized model

通过上述实验结果的分析,可以得出如下结论:

1)采用ER算法对同类指标进行评估能够有效降低模型复杂度,同时保障模型的精度,为后续构建分层BRB模型提供了基础.此外,ER推理过程具有可溯性,能够清晰解释影响指标与性能之间因果关系,有助于洞察处理器各结构对性能的影响.

2)相较于未经过参数训练的初始模型,WOA优化后的性能分析模型精度有了明显的提升,表明了优化模型能够弥补初始专家知识不确定的缺点,增强模型的稳定性与鲁棒性.

5 总 结

针对处理器性能分析过程中出现的指标种类复杂及建模过程不具有可解释性问题,提出了一种融合ER和分层BRB的性能分析模型,通过ER方法底层评估分类指标,降低模型复杂度,提高指标的可靠性,同时将结果作为输入建立分层BRB性能分析模型.初始模型由于专家知识具有不确定性,模型结构不完整且精度存在误差,为了提高模型的精确度,引入了鲸鱼优化算法对参数进行全局优化,与其他机器学习方法对比,精确度与稳定性均有更好的表现,充分说明了本文所提模型的有效性.此外,本文也存在一定的局限性.一方面,模型主要基于影响CPU性能的硬件指标参数进行分析,尚未对CPU能耗讨论,CPU运行过程中产生的能耗也会影响性能分析的结果,另一方面,本文在构建和优化分层BRB模型时,其可解释性也会遭到一定破坏.未来的研究会从以下几个方面做出改进:

1)分析CPU运行能耗的影响因素,测量能耗损失的大小,研究能耗与CPU性能之间变化关系,构建考虑能耗的性能分析模型.

2)利用专家知识构建的专家系统中,加入可解释性约束准则,提高模型的可信度,同时保证模型的合理性与精度.