广珠城际铁路停站组织方案分析
文/潘笑 秦雪锐
1.模型假设与参数说明
1.1 相关条件假设
在城际铁路列车停站方案仿真优化模型构建中,为剔除不必要因素的干扰,本文具体需要假设的前提如下:(1)封闭性假设。本文假设所研究的城际铁路体系是相对独立且封闭的,故只考虑在本线客流量及运营列车停车情况。(2)确定性假设。本文研究是在OD客流、列车起点和终点、列车等级、列车开行数量以及列车编组等参数确定情况下,对城际列车在中间站的停站方案进行优化。(3)能力限制假设。本文假设城际铁路区间通过能力不会对优化后的停站方案造成影响,即线路能力高于列车开行数量。(4)单向性假设。城际铁路上行列车到达终点站后会原路折返成为下行列车,故假设两个方向上列车停站方案相同,只选择其中一个方向进行研究。(5)相似性假设。本文假设所有运行路列车的型号、运行速度、车站停留时间、列车定员等参数相同,且不考虑列车区间越行的情况。
1.2 相关参数说明
本文所涉及的相关参数如下所示:T{ti|i=1,2,…,m}为列车集合,m 为列车数;W={ωi1,ωi2|i=1,2,…,m}为列车停站次数限制集合,其中,ωi1,ωi2分别表示为列车i停站次数下限与停站次数上限;S={sj|j=1,2,…,n}为车站集合,n为车站数;L={lj|j=1,2,…,n}为车站等级集合,lj表示车站j对应的车站等级;F={fj|j=1,2,…,n}为车站服务频率集合,fj表示车站对应的最低停站列车数;C={cj|j=1,2,…,n}为车站能力集合,cj表示车站j对应的最低停站列车数;xij为决策变量,xij=1代表列车i在车站j停站,xij=0代表列车i不在车站j停站。
2.城际铁路优化模型构建
目标函数分析:由于列车停站次数增多会导致列车周转时间延长,运转效率变低,通过控制列车在站停车的次数的方法来使得铁路运输企业的运营效益提高,本文选择以所有列车停站次数只和最少为优化目标。约束条件分析:本文构建城际铁路优化模型主要考虑站点服务频率约束、车站能力约束及列车停站次数约束等几个因素。(1)站点服务频率约束。在城际铁路线路沿线车站分类已知条件下,不同类型车站需要停靠最少列车数各不相同,且在高等级车站停靠的列车数不少于低等级车站。(2)车站能力约束。车站能力约束属于铁路运输设备约束范畴,即单位时间内,某车站内到达与出发的列车数不能超过该站能力。(3)列车停站次数约束。过于频繁的停车,会导致列车全程的平均速度过低,从铁路企业运营效益角度及旅客出行质量角度出发,都需要对列车的停站总次数进行限制,然而,列车停站次数过少又会导致部分客流需求无法满足,故本文对每趟列车的停站次数区间加以限制。综上,构建城际铁路列车停车计划优化模型如下:
3.城际铁路优化模型求解
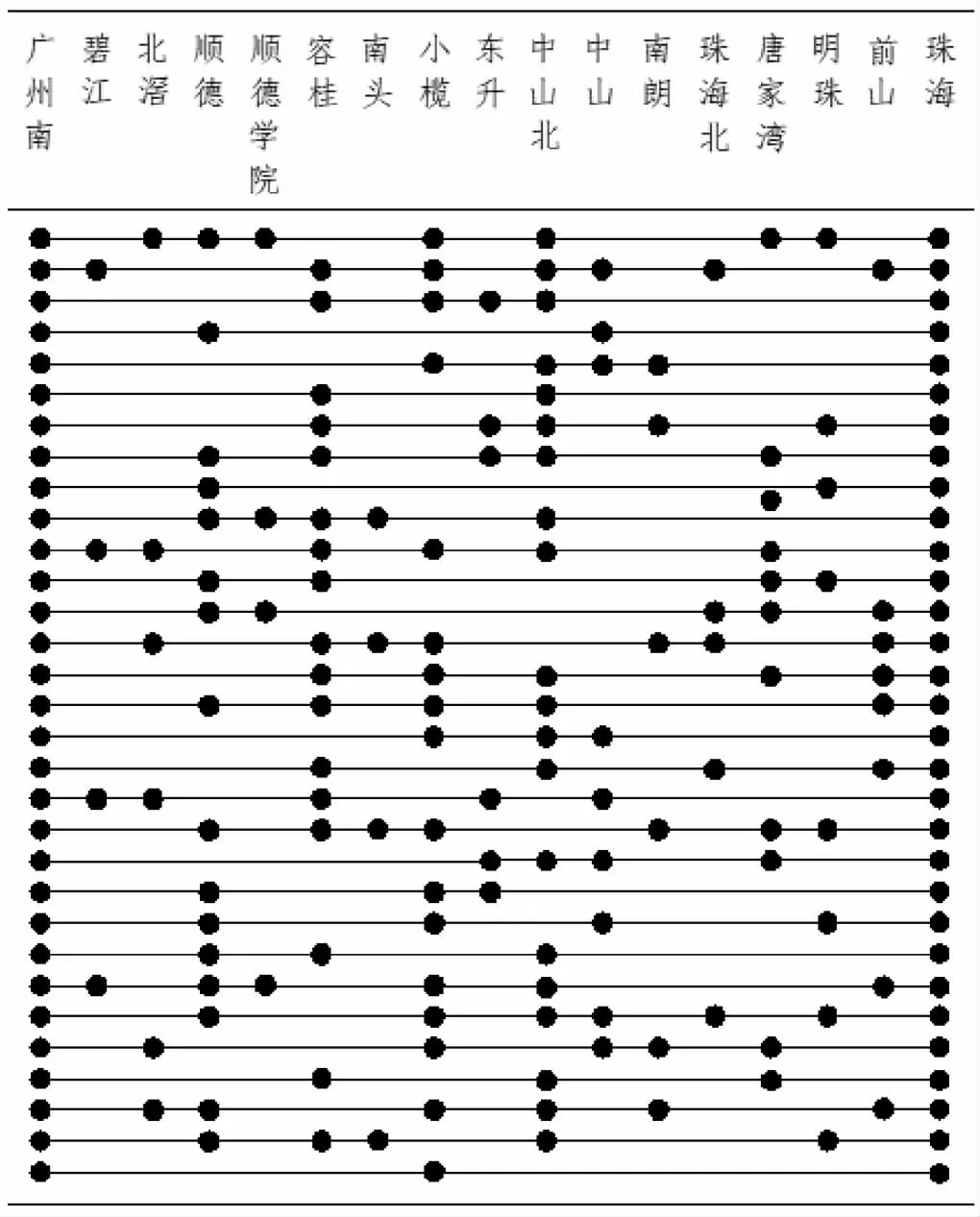
模拟退火算法是模仿工业材料退火过程,将可行解空间内的每一个点视为分子,其对问题的适应程度视为动能,从某一较高的初温状态开始,渐渐降温,以M etropolis准则为依据,进行随机搜索,避免求解过程陷入局部最优,更容易搜索到全局最优。M etropolis法则的中心思想是以概率为凭据,接受新解。温度为T时,当前状态为i,新状态为j。若Ej 相对于传统的优化方法,模拟退火算法可以应用到很多方面的问题之中。它具备较好的总体搜索能力以及较快的求解速度和初值鲁棒性,可以直接使用目标函数来寻求最优解,还具有易于和其他算法结合等优点。相对而言,模拟退火算法还存在难以确定算法内循环次数、收敛的条件要求高、算法参数选取困难等几方面的不足。模拟退火算法实施步骤如下:Step1给定足够大的最初退火温度,随机生成初始解X,确定迭代次数;Step2在温度下Tx,生成新的可行解X'=X+ε,其中ε 为小的均匀分布随机扰动,计算评价函数ΔE=E(X')-E(X),如果ΔE<0,则接受X'为新的可行解,反之,当概率p大于[0,1)区间的任意数,仍接受X'为当前可行解,否则当前可行解则仍为X。重复Step2的内容,直到系统达到平衡状态;Step3根据设定的迭代次数等条件进行降温处理,定义温度下降函数Tk+1←αTk;Step4判断是否满足收敛标准,满足则结束,否则,转Step2。 采用灰色关联分析法对广珠城际的车站进行节点等级划分,选取广珠城际某日各车站发送人数、到达人数、车站所属地区GDP、常住人口数等四个指标对客流节点进行等级划分,具体数据如下参考改年年鉴。设置上述四个指标的权重分别为0.3,0.3,0.2,0.2,以广州南站数据为参考序列,利用SPSS软件进行数据分析得出每个车站数据序列与参考序列的关联度系数ζj∈(0,1)如图1所示。 图1 各客流节点关联度 将上述车站节点划分为三个等级,每个车站所对应的等级划分如表1所示。 表1 广珠城际铁路沿线车站等级划分表 广珠城际可分为主线(广州—珠海)和支线(广州—新会)两部分,该线路日均客流OD数据详见参考文献。在对停站方案进行研究时需要将两条线路分离出来,对于共线部分的客流,根据主线和支线列车开行数量的比例进行划分。根据广珠城际铁路运行列车基本情况,本文设置列车定员为655人,列车运行途中停站为2分钟,列车在站停车次数下限为2次,上限为9次。节点服务频率约束和节点接发停站列车能力方面,目前我国铁路一级节点的最低服务频率一般为20次/天以上,其余相关参数如表2所示: 表2 客流节点相关参数 最大断面客流量是指在线路中断面客流量的最大值,根据文献中相关客流数据,本文假设线路断面满载率为80%,广珠城际铁路主线列车开行数量计算如下式。 采用MATLAB R2019a软件编写模拟退火算法程序求解城际铁路列车停站方案优化模型,设置算法初始温度T0=999,算法结束温度Tf=0.001,马尔科夫链长度Mk=40,温度衰减参数α=0.9,得到列车停站方案结果如图2所示。 图2 广珠城际铁路主线停站方案 图3 广珠城际各个车站列车服务停站次数对比 以列车开车运行对数、车站服务频率和所有列车停站总次数等三个指标为参照,将上述列车停车方案与2013年广州-珠海城际铁路实际停站方案进行对比分析。(1)列车开车运行数量,在实际的停车计划中,本线路主线方向的运行的车辆数为40对,而本文计算得到的优化方案中主线方向的运行对数优化为31对:(2)车站服务频率,除极少数的节点服务频率会出现小范围的增加,绝大部分节点的服务频率都有所降低,这是由于车次运能过盛,列车上座率不足,因此有必要减少列车发车对数。 本文设一级、二级和三级节点的权重分别为0.5、0.3、0.2,由此可求出节点的加权平均服务频率。(3)所有列车停站总次数,实际方案中,所有列车停站总次数为236,而优化后所有列车停站总次数为203,即列车平均旅行速度得到提升。 由表3可以看出优化后的列车运行数量只占原方案的77.5%,由此,减少了铁路企业运营所需的成本;但是由于受到了列车运行数量的限制,运行线路上的节点的平均服务频率也随之降低了2.9%,停站方式个数和停站的总次数也有所减少。综上可知,优化后的方案略优于原方案。C 表3 指标数值表 引用出处 [1]刘君君.考虑旅客快速出行需求的城际铁路列车停站方案优化研究[D].北京交通大学,2019. [2]Yang L,Qi J,Li S,et al.Collaborative optim ization for train scheduling and train stop planning on high-speed railways[J].Omega,2016,64:57-76. [3]李得伟,韩宝明,李晓娟,张洪军.基于节点服务的高速铁路列车停站方案优化模型[J].铁道学报,2013,35(06):1-5. [4]曲思源.基于系统聚类的沪宁城际高铁列车停站改进方案[J].交通运输工程与信息学报,2015,13(02):39-44. [5]黄林尧,吕红霞,杜毓祥等.基于节点重要度的高速列车停站方案优化[J].交通运输工程与信息学报,2017,15(03):49-57.4.实例验证
4.1 车站等级划分


4.2 停站方案确定

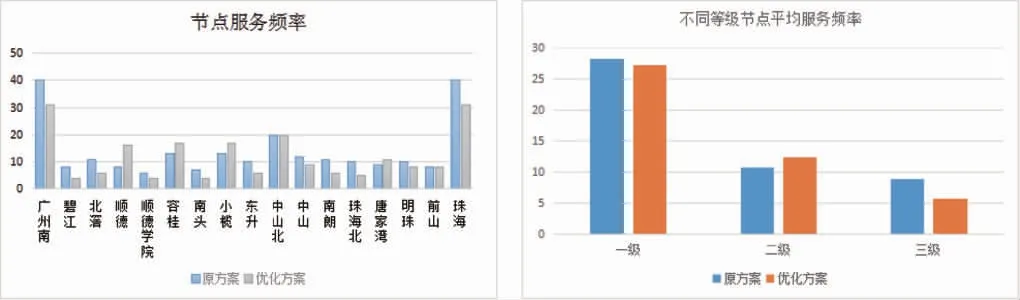
4.3 结果分析与评价


