同心圆锥曲线的性质再探
官一宏
(福建省永春美岭中学,福建 泉州 362618)
类比思想在高中数学教学中扮演着重要的角色,数学中的很多发现都是通过类比得到的.类比可以得到新的结论,但未必正确,需要给出严格的证明.同心圆,由于其对称性而具有很多经典的性质.根据类比思想,同心圆锥曲线应该也有很多经典的结论.我们可以通过类比得到结论,然后用超级画板验证,最后给出严格的证明.
1 同心圆锥曲线的定义
定义设两圆锥曲线有着公共的焦点F,且与F相应的准线f也是公共的,则称这两个圆锥曲线为同心圆锥曲线[1].
2 同心圆的性质
性质1如图1,设圆Γ1和圆Γ2为同心圆,公共圆心为O,作一直线交圆Γ1于A、B两点,交圆Γ2于C、D两点,那么∠AOC=∠BOD.

图1 同心圆
3 同心圆锥曲线的性质
将该性质类比到同心圆锥曲线,则得到:
性质2如图2,设椭圆和抛物线为同心圆锥曲线,F和f分别为它们的公共焦点和相应的公共准线[2],作一直线交椭圆于A、B,交抛物线于C、D,那么∠AFC=∠BFD.

图2 同心圆锥曲线
如图3,利用超级画板验的度量功能,进行动态探究,最后发现当直线AB在椭圆上运动时[3],∠AFC=∠BFD始终成立.

图3 超级画板验证
4 性质的证明


图4 同心圆锥曲线
因为直线l分别交椭圆、抛物线于A、B、C、D,故直线l不可能平行于x轴,则设l:x=my+t,A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),直线FA、FB、FC、FD斜率分别为k1、k2、k3、k4.



直线与椭圆联立整理得:
整理得(a2t2-b4m2)y2+(2mb4+2b2cmt)xy+(b2t2-2b2ct-b4)x2=0.
对上式同除以x2得
同理,齐次联立抛物线与直线l可得


∠AFC=∠BFD等价于∠AFB与∠CFD的角平分线重合.
记∠AFB与∠CFD的角平分线的斜率分别为k1,k2,直线lAB:x=my+n.
设A(xA,yA),B(xB,yB),C(xC,yC),D(xD,yD).
又xA=myA+n,xB=myB+n,得
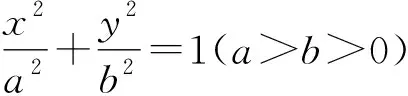
(a2+b2m2)y2+2b2mny+b2(n2-a2)=0.

所以2myAyB+(n+c)(yA+yB)

即b2m(a2+cn)k2+[b4m2-(a2+cn)2]k-b2m(a2+cn)=0.(1)

c2y2-2b2mcy-b2(a2+c2+2nc)=0.

所以2myAyB+(n+c)(yA+yB)

即b2m(a2+cn)k2+[b4m2-(a2+cn)2]k-b2m(a2+cn)=0.(2)
而k1是方程(1)的根,k2是方程(2)的根,但是方程(1)与(2)其实是同一方程,
所以k1=k2. 所以∠AFC=∠BFD.
证法3先证明一个引理:
如图5,设同心圆锥曲线的焦点为F,相应的准线为l,任作直线交椭圆于B,C,交l于E,则EF为∠BFC的角平分线.

图5 椭圆 图6 同心圆锥曲线

下面证明本题的结论,如图6,延长诸线与l相交,对抛物线由引理有EF平分∠DFH,对椭圆由引理有EF平分∠CFG.
从而∠DFC=∠GFH=∠AFB.证毕.
通过类比同心圆的性质,可以得到同心圆锥曲线的性质[4],然后利用超级画板进行验证,再用解析法或者几何法给出严格证明,这就是本文的研究思路.我们知道,同心圆有很多漂亮的性质,那么,这些性质类比到同心圆锥曲线是否成立呢?这有待于读者的进一步探索.

