基于有序聚类不等分法的路面状况评价
夏 晶,马杰灵,吴姗姗
(桂林电子科技大学 建筑与交通工程学院,广西 桂林 541000)
据统计,截至2020年底,我国养护公路总里程已经达到了514.40万km,占总里程的99%,路面养护已成为中国公路发展的重中之重[1]。因为车辆的超载行为、不同地质环境对路面的影响以及公路交通承载量过大等因素,我国许多水泥混凝土路面在未达到预先设计的使用寿命之前,就出现了较为严重的损坏。养护措施的科学决策是建立在对路面状况的准确评价的基础之上,路面状况评价的准确性很大程度上取决于路段划分的科学性。目前路段划分常用的方法有等长划分法和不等长划分法。在我国公路标准中将路面评价的基本单位定为1 km。在路面进行实际养护时,工作人员也经常应用整公里处作为路段划分的基本单位从而等长划分路段。但这种方法认为在每公里内,该路段具有相似的路面特性,使得这种方法存在一定程度的盲目性。而不等长路段划分法是一种能考虑到病害的分布特点以及路面的使用情况等综合因素,并利用数学的分析方法对收集到的数据进行有效的处理,并将路面特性相似的路段划分为同一类路段的划分方法。这种方法的优点就是使每个路段具有相似的特性,缺点是路段划分过程较复杂,容易造成路段过短。国内许多学者已经致力于这方面科学研究,农家萍等[2]以5项路面养护指标来评判路面的属性为基础,提出一种基于传递闭包法的数学手段,来进行路面划分。蒋红妍[3]将编网法运用在道路中,利用模糊相似系数的构建方法建立了路段变长的划分方法。王佳等[4]用有序聚类方法在1 km路段中扩大分割段数,用vb制作了养护路段有序聚类模型。马士宾等[5]等利用损失度函数的概念,将有序聚类法的原理和路面状况评价中运用到的权重思想融入到大中修养护路段长度划分过程中。牛晓霞等[6]等对于目前道路评价中对于路段划分存在的不足,提出了基于有序聚类的路面划分方法。
目前,国内对路面划分的研究确实取得了一些成果,但还存在以下不足:(1)研究成果所运用的实际工程数据过少,实验结果的可靠性还需要进一步验证。(2)研究人员在进行路面划分时所考虑到的影响因素不够全面,未考虑我国养护工作的实际可操作性。
因为在Fisher算法中,随着分类数k的增加,损失度函数会逐渐减小,而在实际应用中,分类数k无法确定,如何在聚类中确定最佳的聚类数就成为值得研究和探讨的问题之一[7-9]。以兰海高速公路的水泥混凝土路面的路面病害图像信息为研究对象,考虑到路面的连续性,将有序聚类分析与Fisher算法相结合,按照路面破损相似程度不同来作为路面划分的依据,并提出了确定最优分类数k的方法,验证了该方法的可行性,为水泥路面路段划分提供更客观准确的方法。
1 有序样本聚类法的基本原理
将一群具象或抽象的研究对象的集合划分成若干个类别的过程称作聚类。这些研究对象的数据是聚类生成的集合,同一组集合中研究对象的数据类型相似度高,但与其它组集合中研究对象的数据是不同的[10]。聚类分析是人类在研究样本分类时用到的一种重要的统计分析方法,目的是收集相似的数据作为分类的依据。在实际应用中,有时样本之间的顺序不能改变,且同一分类中样本的排序是相邻的这类问题需要运用到有序聚类分析方法。有序聚类就是在一条“高速公路”路段上寻找一种分割方法,可以使分段后的合并部分之间的差异尽可能小,而“合并路段”之间的差异也越大越好。这种分割方法不破坏样本中原有的顺序,被称作有序样本的最优分割。根据里程分布,路段是一个有序的样本,它的顺序是不能改变的。将有序样本聚类分析方法应用到路面破损状况评价的路段划分中,重点在于利用了其“有序”的特点,在维持公路里程桩号顺序不发生改变的情况下,将几个路面损坏程度和损坏类型相似或相同的路段聚集到一个合并路段中。并且根据我国规范中水泥混凝土路面养护的特点对分类结果进一步改进,使分类结果进一步简化,得到更佳的路面划分方案。
Fisher最优分割方法是目前国内外常用的一种有序聚类统计分析方法,它是1958年由费舍尔(Fisher)提出的[11]。主要思路是先将所有样本看作为一个种类,并且在所有的分类必须是全部相邻的条件限制下规定其损失函数。按照它的分类规定,在分类内使偏差平方和达到最小、分类间的偏差平方和达到最大的思想下,分类逐渐增加。方差分析是损失函数的基本思想,其定义是偏差平方和。当分类结果正确时,归属于同一类别的样本值与该类别的平均值之间的偏差平方和应比较小,而不同类别的类直径之间的偏差平方和应比较大。
2 有序聚类法实现步骤
2.1 数据处理
由于偏差平方和法计算类直径受指标的维数和数值的影响,在计算类直径之前,有必要对各个指标进行正规化处理,主要是对数据样本进行归纳和统一,通过变换数值的范围,将原始数据矩阵中任意一列的最小值为0,最大值为1,使剩下的值均处于0与1之间[12]。记为
(1)
2.2 计算直径系数矩阵和误差函数
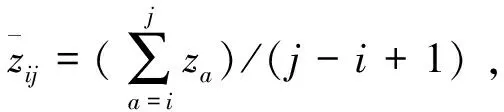
(2)
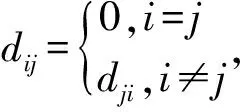
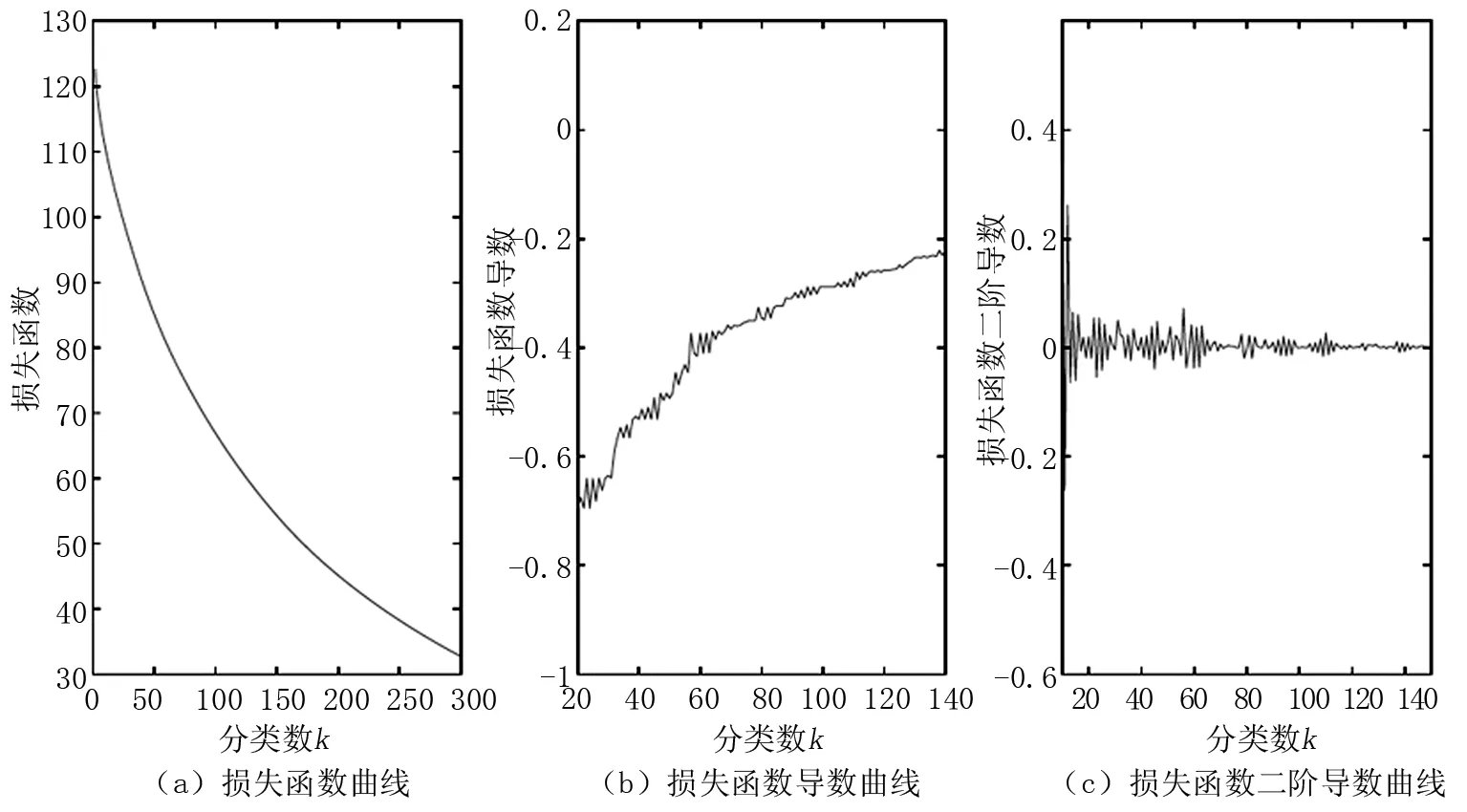
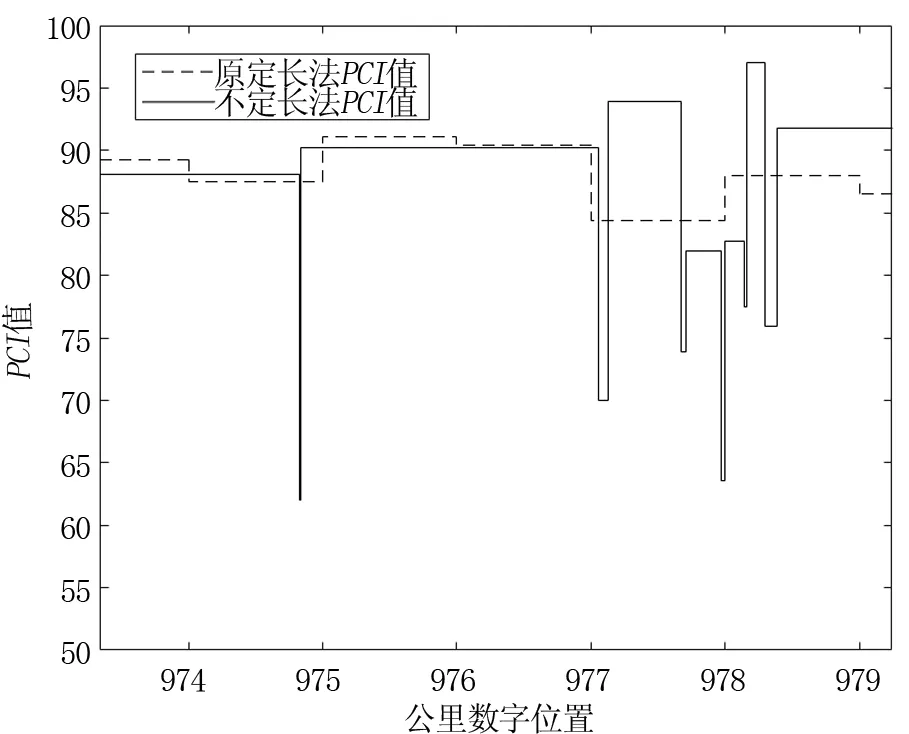
将n个样本数据分为k个类别,i记作第i号样本。假设其中的某种分法记为b(k,n):{i1=1,i1+1,…,i2-1},{i2,i2+1,…,i3-1},…,{ik,ik+1,…,n},(i=1 (3) 当k=2时,需要找到一条分界线,将所有样本分为两类,而b(2,n)则是一种在所有可能的分界之间能使误差函数最小化的方法。对n进行归纳,于是 (4) 值得注意的是,只有完成n-1个有序样本分成k-1个类的最优分割,才能确定n个有序样本能够分成k个类的最优分法,但表示第k层分类是在k-1类的分类上添加一层分割[15],这种最小二分法只是众多种分割方法中的其中一种,只属于局部最优法,并非全局最优。为了使损失函数能够达到最小,分类数k和分类数为k-1的结果可能存在很大不同。可以使用这些方法进行分类的前提是知晓初始样本的分类数k。但是在实际应用中是无法提前知晓样本的分类数。确定分类数的方法是通过损失函数的导数求出拐点位置,从而确定最佳分类数,因为损失函数误差函数是由多个离散点构成的,所以使用差分来代替导数 =L[b(n,k-1)]-L[b(n,k)] (5) 在Lk曲线变化趋于平稳段中选出变化较大的某个点作为分层数k,但可能存在不止一个点。以损失函数拐点的确定方法为基础,引入基于k-mean聚类的二阶差分[16]的理念,提出适用于路面划分的基于有序聚类的二阶差分统计法,以确定最优分类数k的值,避免使之陷入局部最优解。构造如下统计量 Z=[W(k+1)-W(k)]-[W(k)-W(k-1)] =Wk+1-2Wk+Wk-1,k≥2 (6) 其中:W(k)-W(k-1)可以看成是当聚类数从k-1增加到k时,合并类平均、类内平方和的离差。若k为最佳聚类数,有Z>0。而Z越大,就意味着当把k类增加为k+1类,会使组内平均指数变得更大,因此就放弃让W(k)达到最小作为最终结果,让Z>0达到最大但W(k)较小的k定为最佳聚类数。显然,当使用这种方法选取了k之后,如果增加聚类的数目,聚类效果会变差,则该聚类数k作为最佳聚类数。同时结合零波动数据[17]的概念,保证剔除粗大误差的基础上保证Z达到最大,以达到全局最优解的目的。 选取兰海高速公路964~984 km处水泥混凝土路面作为测试路段,通过现代检测车所采集的路面破损图像并位进行路面病害统计分析,以6 m前进方向为统计单位,利用路面病害标记软件得出测试路段病害统计结果输出作为变量矩阵。 首先对该矩阵变量进行规格化处理,获得在不同分类数下的最优分割结果表(见表1),按照算法进行分类,从损失函数导数曲线(见图1)可以看出变化较大的分类数有k=31,34,37,45,46,51,52,56,57,可以看出曲线中变化较大的点过多,这时引入二阶导数概念[18],若D(k)为最佳分类数k的二阶差分值,则存在D(k)>0,且D(k)为零波动范围内二阶差分最大值,其中当k=34,52,51,60时,W(k)<0;当k=51时,二阶差分曲线值处于零附近波动数据范围且为最大值。按照表1,输出k=51时的路面破损状况评价值。 图1 损失函数及其一阶、二阶导数曲线 根据《公路技术状况评定标准》(JTG 5210—2018)中所提出的路面状况指数。 PCI=100-a0DRa1 (7) 式中:DR为路面破损率,a0、a1为系数,其具体数值及其他系数均选取自《公路技术状况评定标准》(JTG 5210—2018)。路面损坏状况指数等级划分标准见表2。 表2 公路破损状况等级划分标准 通过按照上式计算得出最佳分类的不等分路段PCI值和以评价标准中的1 km检测单元路段PCI值,图2展示了兰海公路部分的PCI阶梯图对比。根据我国养护方法中提到:当路面破损状况评价的结果为良好及以上时,只需要进行日常的养护和局部修补措施;当路面评价的结果为中及中以下时,则需要进行路段修复或其他的路面大中修的改善措施。从图2可以看出,按照1 km等长路段计算出的PCI值均为良及以上,全路段只需简单的日常养护,但按照不等长路段计算出的PCI值,其中973.827~973.833 km处和976.991~976.997 km处PCI值仅为60.03和61.08,而按照评价标准以整公里为统计单位计算的974和977 km处PCI值为88.5和85.4,实际数值远低于原评价标准PCI值,当该路段路面等级在中及以下时,若只采取日常养护,路面得不到及时的处治,可能会造成病害越来越严重,路面舒适性大打折扣。其他路段PCI值与评价标准PCI值均存在一定差异,PCI值的差异很大程度上会影响养护方案的制定,有效且准确的路段划分是正确评价路面破损状况的重要因素。 图2 评价标准PCI值与不等分路段划分PCI值对比图 将有序聚类最优分割法应用于路段划分中,在一定程度上避免了决策者在经验划分路段的方法中所产生的主观意识造成的误差。不等长路段划分方法可以更加细致地统计出不同等级相应的路段,既能更准确地反映路面的实际破损状况变化,也能指导养护工作实际。 (1)针对当前我国路面评价分析中对于路段划分中存在的不足,提出了基于不等分法路段划分的路面状况评价方法。将Fisher算法与有序聚类分析相结合,建立了用于确定路段划分的有序样品最优分割方法,与常规等长路段PCI值的计算结果进行比对,使用等长法进行路面划分的路面状况评价无法准确地显示路面破损状况的变化情况,不等长法则能够真实反映局部路段路面状况的变化,对于路面的养护具有更科学和客观的借鉴意义。 (2)每个检测单元的长度越小,病害统计的准确度就越高。但在有序聚类分析法中就更容易出现离散程度大,相邻的单元的路面属性相似程度小的情况,导致分类数过多,计算量过大,在实际应用中造成一定困难。如何在考虑最小施工单位等客观条件,选取合适的检测单元,以及有序聚类算法中的分类数组的限制条件的设定,使之既能准确反映路面破损状况又能便于养护措施的制定是下一步需要完成的目标。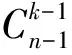
2.3 N[b(k,n)]的递推公式
2.4 确定分类数k方法
3 有序样本最优分割法在路段划分中的应用

4 结束语

