基于粒子群算法的烟草商业企业物流设备备件优化研究

丁宇轩

（陕西省烟草公司西安市公司，陕西 西安 710061）

面对工业4.0 的环境，我国烟草商业企业物流设备管理模式仍处于较低水平。设备管理主要包括备件管理、运行管理和检修管理三大部分。其中，备件管理作为设备管理中的一个重要部分，就是用较低的费用来合理地管理备件库存储配，把设备突发故障造成的损失降到最低。传统的备件预测方法主要依靠管理者的主观经验来判定，但历史数据显示，预测结果与实际生产维护需求之间存在着较大差异。因此，如何找到设备可用度与备件费用之间的平衡点，是企业当前物流设备管理中亟需解决的问题。从数学建模的本质来看，烟草商业企业物流设备备件优化配置问题就是考虑了费用约束条件下的非线性规划问题。

目前解决具有约束条件非线性规划问题的常见智能算法有模拟退火算法SAA（Simulated Annealing Algorithm）、 模拟植物生长算法PGSA（Plant Growth Simulation Algorithm）、 遗 传 算 法GA（Genetic Algorithm）、蚁群算法ACA（Ant Colony Algorithm）、 粒子群算法PSO（Particle Swarm Optimization）等。本文结合烟草商业企业物流设备的物理性质、寿命与可靠性等参数，提出了一种基于标准PSO 的备件优化配置模型，并结合企业实际算例，应用模型进行仿真求解。仿真结果表明，本文提出的备件优化配置模型具有较好的预测效果和准确性。

1 当前企业备件管理问题分析

（1）受到企业自身物流管理水平的限制，当前备件管理缺乏成本意识，以粗放型管理为主。备件的采购计划主要以管理者的主观经验判定。在实际备件管理中存在需求放大的现象，即采购数量宁多勿少，然而，备件的消耗规律和实际维护供应存在较大差异。部分备件的消耗速度偏慢，导致存放时间超过1 年以上，积压库存占用大量企业资金，违背了企业物流管理中经济合理的原则。而部分备件的库存量又不够，且订货周期偏长，影响物流作业，甚至出现停产现象。

（2）当前备件管理模式缺乏科学方法，与设备综合管理的统一协调不够。备件的管理水平仍处于初级阶段。虽然省级物流管控平台已落地应用，实现了设备及其备件资料的信息化管理，但该系统的备件管理模块只涉及备件的出入库数据，缺乏对数据深层内涵的分析与研究。

（3）当前设备维护人员适应新知识、新要求的能力不足。目前的工作重点主要为设备的事后维修和定期保养检修，欠缺对备件寿命与可靠性的相关分析与研究，无法更好地指导设备维护工作。只有充分了解设备各备件或零件的寿命与可靠性，学习概率统计方法，才能成为一名复合型设备维护技术人员。

2 备件优化配置模型的建立

2.1 模型的基本假设

影响烟草商业企业物流设备备件优化的指标有很多，如设备的使用可靠度、失效概率、失效强度、作业环境、费用等。本文基于以下假设建立使用可靠度和费用模型：（1）物流设备为串联系统，当所有组成部件均正常工作时，设备才能正常工作。（2）物流设备备件在运输、储存的过程中处于完好状态。（3）物流设备备件更换时间在此模型中忽略不计。（4）零部件的可靠度分布函数符合威布尔分布。

2.2 备件使用可靠度

以可靠性为中心的维修RCM（Reliability Centered Maintenance）是近年来被广泛接受的一种应用系统工程方法的维修理论。使用可靠度又是RCM 理论中最为重要的一项指标。使用可靠度指备件在给定工况和时间下，完成规定任务的能力的参数。在模型的基本假设中，零部件的可靠度分布函数符合威布尔分布。威布尔分布最早由瑞典工程师W.Weibull 根据n 环链条在其最弱环节失效的模型而推导得出的一种适用于一般材料及机械零件寿命的统计分布。威布尔分布模型分为三参数和二参数两种，其中三参数模型的参数估计难度较大，在实际应用中仍以二参数模型为主。二参数模型的另一个优点在于不需要提供协变量的寿命预测，仅需失效历史数据即可推算出零部件的可靠度以及失效率。二参数威布尔分布的概率密度函数为：

其中，β为形状参数；η为尺度参数，也称零部件的特征寿命；t 为时间或循环次数。考虑物流设备的实际运行状态，对比产品全生命周期的“浴盆曲线”图，得出当前企业物流设备处于产品全生命周期中的随机失效期，瞬时失效率是一个常数，因此形状参数β=1。此时，威布尔分布转变为指数分布。假设企业物流设备由个零部件串联组成，则第i 个零部件具有m 个备件，且备件的型号相同，则第i 个零部件的使用可靠度为：

其中，λi为第种部件备件的失效率。因此，物流设备备件使用可靠度为：

在备件优化配置中，模型要求R ≥R0，其中R0为备件使用可靠度的最低值。

2.3 物流设备备件费用约束

在备件优化配置中，费用主要涵盖了采购费用、存储费用、备件缺货损失费用等。本模型为便于算法计算，将费用约束统一简化为采购费用。因此，模型的费用约束可表示为：

其中，Ci为物流设备第个备件的单价，mi为第i 个备件的采购数量。在备件优化配置中，模型要求C ≤C0，其中C0为备件采购费用的最大值。

2.4 模型的目标函数

物流设备备件优化配置的目标为在备件使用可靠度和费用的约束下，增加物流设备的可靠度，降低备件的采购费用。模型的目标函数如下所示：

3 基于PSO 算法的备件优化配置模型的求解

3.1 粒子群算法基本原理

粒子群算法PSO（Particle Swarm Optimization），也称微粒群优化算法，是一种基于群集智能的仿生进化算法。PSO 受到鸟群捕食行为而启发。算法采用速度—位置搜索模型。在标准PSO 中，速度vi=(vi1，vi2，…，vin)决定粒子在搜索空间中单位迭代次数的位移。PSO 随机初始化一群粒子，其中第i 个粒子在维空间的位置可以表示为xi=(xi1，xi2,…，xin)。每个粒子在迭代过程中通过跟踪个体极值pbesti=(pbesti1，pbesti2,…，pbestin)与全局极值gbesti=(gbesti1，gbesti2,…，gbestin来更新其速度和位置。公式如下：

其中，rand（）是[0,1]之间的随机数。c1和c2为常数，称为学习因子，一般在[0,2]之间取值。ω为惯性权重，对调节算法的性能有着重要作用，较大的ω值有利于开展全局寻优，而较小的ω值有利于局部寻优。因此，在迭代中设计一个线性递减的ω函数，可以在算法运行初始阶段开展全局搜索，定位到全局最优点附近，之后开展局部搜索，精确找到全局最优解。ω的函数形式通常表达为：

其中，ωmax和ωmin分别为惯性权重的最大值和最小值，Tmax为算法的最大迭代次数。通常建议采用ωmax=0.9 线性递减到ωmin=0.4 的设计来获得较好的算法性能。

3.2 适应度函数的构造

本模型应用惩罚函数的思想来构建适应度函数，将有约束优化问题根据约束特性构成惩罚函数并使其加到原目标函数上，从而转化为无约束优化问题来处理。模型的适应度函数如下：

其中r 为惩罚因子（加权因子）。

3.3 模型的求解步骤

模型的求解步骤如下：

（1）初始化粒子群的位置xi和速度vi，包括算法最大的迭代次数和种群中的粒子个体数目size。

（2）计算粒子的适应度值Ø(xi)。

（3）根据初始粒子适应度值Ø(xi)寻找个体极值pbesti和群体极值gbesti，即当前单一备件的最优配置以及当前所有备件组合的最优配置；

（4）根据公式进行迭代寻优，更新粒子的位置xi和速度vi，并根据新粒子的适应度值Ø(xi)更新个体极值pbesti和群体极值gbesti。

（5）分析算法是否满足结束条件，即误差足够好或者到达最大迭代次数N，如果满足结束条件则算法退出，输出最优解，即当前所有备件组合的最优配置，否则，返回步骤（2）重新计算粒子的适应度值Ø(xi)。

4 算例应用

当前，企业备货及分拣系统主要有5 种备件，其采购单价与使用可靠度如表1 所示。要求物流设备备件可靠度R0=0.9，备件采购费用元C0=45000 元。

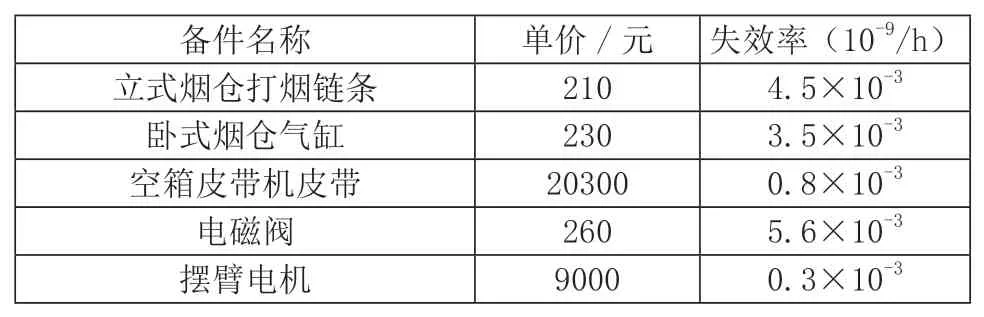
表1

算法参数具体如下：最大的迭代次数N=2000；粒子个体数目size=24；学习因子c1和c2设置为2，分别影响局部最优解和全局最优解；设计有关惯性权重的线性递减函数，ωmax和ωmin分别设置为0.9 和0.4。算法终止的阈值设置为e-25，当连续两次迭代中对应种群最优值变化小于此阈值时，算法终止。通过MATLAB 软件编程实现物流设备备件优化配置，程序随机仿真运算20次，取出现次数最多的解为模型的最优解。经统计，在算法运行到380 ～400 步时能够找到备件配置的最优解，得到最优配置为[5,5,1,8,2]，总费用为42580 元，使用可用度为0.94。

5 结语

物流设备备件优化配置问题是一个较为复杂的组合优化问题，而且影响因素比较多。本文仅从备件使用可靠度和备件费用为约束进行了深入的建模分析，基于这两个约束，给出了基于粒子群算法的烟草商业企业物流设备备件优化数学模型。根据实际算例的应用，发现粒子群算法在解决物流设备备件优化配置问题时效果较好，其收敛速度较快，全局寻优能力较强。