基于FOD-ML的干旱区土壤有机质含量估算

孜尼哈尔?祖努尼江　尼加提?卡斯木　拓跋凯薇

摘要：为探究基于分数阶微分（fractional order derivative， FOD）预处理的光谱反射率与土壤表层有机质含量之间的响应机制，以新疆乌鲁木齐县安宁渠镇土壤冠层光谱为数据源，采用G-L分数阶微分方法对高光谱数据进行0～2.0阶次（间隔0.2）预处理，并利用任意波段组合算法，计算基于分数阶微分预处理光谱的比值光谱指数、归一化光谱指数和差值光谱指数，通过竞争性自适应重加权（CARS）算法筛选土壤有机质含量的敏感波段及光谱指数等，与3种机器学习（machine learning， ML）算法（ANN、KNN和SVM）相结合，构建基于分数阶微分和机器学习方法的土壤有机质含量估算模型，并进行模型验证。结果表明：基于0～2.0阶次的两波段光谱指数与土壤有机质含量之间均呈现极显著相关，基于原数据和0.2阶预处理的NDVI和RVI相关性系数r超过0.80。该研究基于0.2阶NDVI指数的K近鄰算法模拟土壤有机质含量能力表现最佳，估算模型精度分别为决定系数（R2）为0.73，均方根误差（RMSE）为2.11g/kg，相对分析误差（RPD）为2.23。为遥感技术提供理论支持，实现对土壤肥沃程度的精准监测和评估，推动智慧农业的发展。

关键词：干旱区；土壤有机质；分数阶微分；机器学习

中图分类号：S27： O433.4

文献标识码：A

文章编号：20955553 （2023） 11020109

Estimation of soil organic matter content in arid region based on FOD-ML

Zinhar Zunun Nijat Kasim Tuoba Kaiwei

（1. Institute of Resources and Ecology， Yili Normal University， Yining， 835000， China；

2. College of Biology and Geography， Yili Normal University， Yining， 835000， China）

Abstract：In order to investigate the response mechanism between spectral reflectance and soil surface organic matter content based on fractional differential pre-processing， this study used soil canopy spectra of Anningqu Town， Urumqi County， Xinjiang as the data source. The G-L fractional differential method was used to pre-process the hyperspectral data with orders ranging from 0 to 2.0 （with an interval of 0.2）. The ratio spectral index， normalized spectral index， and difference spectral index based on fractional differential pre-processing were calculated using arbitrary band combination algorithms. The competitive adaptive reweighted sampling （CARS） algorithm was used to screen sensitive bands and spectral indices for soil organic matter content， combined with three machine learning algorithms （ANN， KNN， and SVM）， a soil organic matter content estimation model based on fractional differential and machine learning methods was constructed， and model validation was performed. The results showed that there was a significant correlation between the spectral indices based on 0-2.0 orders and soil organic matter content. The correlation coefficients （r） of NDVI and RVI based on the original data and 0.2 order preprocessing exceeded 0.80. The K-nearest neighbor algorithm based on the 0.2 order NDVI index exhibited the best ability to simulate soil organic matter content， with a coefficient of determination （R2） of 0.73， a root mean square error （RMSE） of 2.11 g/kg， and a relative analysis error （RPD） of 2.23， respectively. The study can provide theoretical support for remote sensing technology， achieve accurate monitoring and evaluation of soil fertility， and promote the development of smart agriculture.

Keywords：arid area; soil organic matter; fractional differentiation; machine learning

0引言

土壤有机质（Soil Organic Matter， SOM）是土壤固相部分的重要成分，是植物生长过程中所需营养物质的供源，也是评价土壤保肥性能的重要指标［14］。因此，土壤SOM含量的快速准确监测可为土壤状况的改良、完善和优化土壤施肥措施，以及对精准农业可持续发展提供理论基础。目前，随着高光谱遥感技术的发展，在国内外以其规模大、实时观测、客观性强、成本低、无损和高效等优势被广泛采纳于土壤重要参数的定量估算［57］。

对土壤有机质遥感定量监测中，前者利用土壤表层光谱数据与其有机质含量进行了一系列的相关分析以及土壤有机质含量估算研究，并取得了较好的研究者成果。Krishnan等［8］采用4种不同土壤光谱反射率与其SOM含量进行相关性分析，研究表明土壤有机质含量最佳波段为0.62μm和0.56μm，敏感波段范围集中于可见光波段区域，而NIR部分没有出现明显光谱特征；Hummel等［9］对土壤样品光谱反射率进行了倒数对数等数学变换，分析了光谱反射率预处理前后的变化以及与土壤有机质含量的响应，并构建了相应的多元逐步回归估算模型；Conforti等［10］收集了不同地区土壤样品（共215个），通过偏小二乘回归算法构建了土壤有机质含量PLSR模型，并在估算模型的评价精度上取得了一定的研究成果；尚天浩等［11］利用标准正态变量、峰值归一化、一阶微分、对数的倒数和倒数等5种方法对高光谱进行数学变换，对敏感波段进行最优建模变量提取；何少芳等［12］通过生成式对抗网络方法生成了等量的新数据，利用交叉验证岭回归、PLSR和BP神经网络等算法，建立估算模型并进行了精度验证；尼加提·卡斯木等［13］通过400～2400 nm范围的光谱数据进行两波段组合优化计算，构建最佳波段组合的植被指数，并构建了基于波段组合优化植被指數的土壤SOM估算模型；栾福明等［14］分别建立了基于敏感光谱波段信息的多元线性逐步回归模型和人工神经网络模型，分析了不同建模方法再土壤有机质含量估算中的应用。尽管诸多研究学者对土壤SOM含量的估算中，进行了大量的高光谱数据的数学变换以及计算相应的植被指数，进一步对两波段植被指数完成了波段组合优化等；研究表明土壤光谱反射率特征随着土壤组成成分的多样性而具备一定的差异性，因此不同区域土壤参数估算研究成果相互应用可能呈现一定误差［15］。在此问题上，试着利用波段组合优化的植被指数，寻找研究区最佳敏感光谱指数，也是该研究的核心部分。对解决模型参数多重共线性和建模复杂性等问题，孙倩等利用PLSR方法，发现了多元线性回归、主成分分析、典型相关分析等方法的优点集成于PLSR算法当中，对模型参数的筛选，PLSR算法具有一定优势，在土壤参数筛选与估算具有一定的意义［16］。

因此，本文以新疆乌鲁木齐县安宁渠镇土壤有机质为研究对象，对采样点土壤样品进行室内测定获取土壤有机质含量和光谱数据采集，试着对土壤光谱数据进行G-L分数阶微分（间隔0.2）预处理，比较光谱预处理前后对任意两波段组合的植被指数影响，并分析不同阶次所对应的植被指数与土壤有机质含量的关联程度，利用竞争性自适应重加权算法筛选非多重共线性的敏感植被指数，结合不同的机器学习算法，建立研究区最优的土壤有机质含量估算模型，并在一定程度上提高模型的精度，对研究区田间尺度快速、准确地评估土壤肥力提供方法依据。

1材料与方法

1.1研究区概况

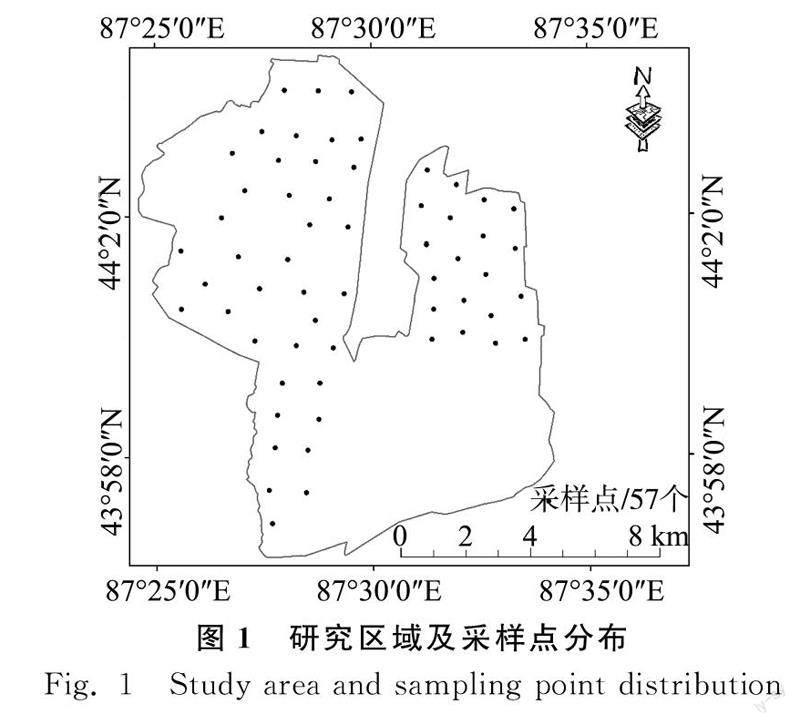
研究区位于乌鲁木齐市北郊的冲积平原上，地势平缓，地理坐标为87°25′～87°30′E，43°57′～44°06′N，图1为研究区采样点分布区域；地处中温带干旱气候区，光热充足，土壤肥沃，适合一般的农作物、蔬菜和果树生长［1718］。该区域水资源丰富，既有水质良好的地下水资源，又有纵贯南北的和平渠提供的地表径流，形成井渠双灌的地方特色，为农牧业的丰收奠定了良好的基础［1920］。

1.2数据采集与处理

土壤样品的采集时间为2017年10月15日，针对乌鲁木齐市安宁渠蔬菜基地研究区典型景观特征，设置5m×5m样方。利用GPS记录每个样方位置，采用5点混合法进行样品采集，土壤样品采样深度为0～10cm，共计57个土壤样品。土壤样品带回实验室并进行自然风干、研磨后，过2mm孔筛分为两部分，分别用于室内高光谱数据的测定及土壤有机质的化学分析。其中，土壤有机质质量比采取重铬酸钾容量—硫酸氧化法进行测定［21］。

因环境影响因素的存在，易在边缘波段350～399nm和2401～2500nm出现较大噪声，对室内测定的高光谱数据需要进行噪声去除处理。利用常用的Savitzky-Golay滤波方法进行剩余光谱数据（400～2400nm）的平滑处理；此后通过Matlab2014采用分数阶微分一元函数差分（Grünwald-Letnikov， G-L）［2223］实现光谱反射率的0～2阶之间运算，G-L分数阶微分表达式如式（1）所示。

d^vf（x）/dx^v≈f（x）+（-v）f（x-1）+（-v）（-v+1）/2f（x-2）+…+Γ（-v+1）/m！Γ（-v+m+1）f（x-m）（1）

式中：

x——对应点的值；

v——阶数；

Γ（·）——Gamma函数；

m——微分上下限之差。

1.3敏感植被指数的筛选

光谱指数是通过目标物的光谱特征，对波段反射率进行组合计算，不仅能充分考虑波段之间的相互关系，还可以有效地提高与目标物之间的度量关系［24］。在前人研究基础上，通过对光谱全波段信息多种方式组合计算，利用RVI（Ratio Vegetation Index）、NDVI（Normalized Difference Vegetation Index）和DVI（Difference Vegetation Index）构建任意两波段组合二维光谱指数，达到波段组合优化的植被指数［25］。最佳敏感植被指数的选择中，先利用基于分数阶微分处理的光谱数据构建任意两波段组合的二维光谱指数，并与土壤有机质含量进行Pearson相关性分析，分别筛选相关系数通过0.01水平显著性检验的RVI、NDVI、DVI，计算公式如式（2）～式（4）所示。

比值植被指数

RVI=R_λ1/R_λ2（2）

归一化植被指数

NDVI=（R_λ1-R_λ2）/（R_λ1+R_λ2）（3）

差值植被指数

DVI=R_λ1-R_λ2（4）

式中：

λ——400～2 400 nm范围内任意波长；

R——波长对应的反射率。

为消除共线性光谱指数的存在问题，本文采用竞争性自适应重加权算法（Competitive Adaptive Reweighted Sampling， CARS）进行精细的筛选。CARS算法是通过自适应重加权采样（Adaptive Reweighted Sampling， ARS）技术选择出偏最小二乘回归模型中回归系数绝对值大的波长点，去掉权重小的波长点，利用交互验证选出均方根误差（Root Mean Square Error， RMSE）值最低的子集，可有效寻出最优变量组合［26］。

1.4估算模型的建立与验证

ANN（Artificial Neural Network， ANN）是指由大量的处理单元（神经元）互相连接而形成的复杂网络结构，是对人脑组织结构和运行机制的某种抽象、简化和模拟［27］。以数学模型模拟神经元活动，是基于模仿大脑神经网络结构和功能而建立的一种信息处理系统。KNN（K-Nearest Neighbors， KNN）是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。如果一个样本在特征空间中的K个最相似（即特征空间中最邻近）的樣本中的大多数属于某一个类别，则该样本也属于这个类别［28］。SVR（Support Vector Regression， SVR）是支持向量机（Support Vector Machine， SVM）算法来计算出来的回归方法，是输入标签连续值时选取的模式［29］。

对建立的模型进行稳定性和预测能力的验证，主要是以最高的决定系数（Coefficient of Determination， R2）和最低的均方根误差（Root Mean Square Error， RMSE）来决定，表明数据拟合效果；相对分析误差（Relative Percent Deviation， RPD），指示模型的预测能力，计算过程是标准偏差（Standard Deviation， SD）与估计标准误差（Standard Error of Prediction， SEP）之比。根据模型的预测能力，RPD值有三种情况：（1）RPD的值超过2.0，说明该模型具有较好的预测能力；（2）RPD值在1.4～2.0之间，代表具有一般预测能力；（3）RPD值小于1.4，说明其预测能力较差。

2结果与分析

2.1数据统计及光谱特征分析

对土壤有机质含量估算模型的建立与精度验证，将采样数据分成建模集和验证集（表2）。分析可知，研究区土壤样品有机质含量最大值为31.78g/kg，最小值为2.70g/kg，标准差为5.79g/kg，数据的离散程度达到53.17%；随机选择构建的建模集土壤有机质含量最大值为31.78g/kg，最小值为4.39g/kg，标准差为6.37g/kg，数据的离散程度达到53.82%；验证集土壤有机质含量最大值为15.79g/kg，最小值为2.70g/kg，标准差为3.19g/kg，数据的离散程度达到36.54%；总数据集的变异系数恰好介于建模集与验证集之间，数据离散程大于36%，属于高度变异［23］。

据土壤养分含量分级标准［28］，将采样区土壤有机质含量分为极高、高、中、低、极低等5个等级，对不同等级对应的光谱反射率进行加权平均，并作为该等级的光谱反射率值。图2是基于不同等级的土壤有机质含量对高光谱反射率的影响关系，分析可知，在红边波段范围对土壤有机质响应比较明显，尤其是在1 500～2 200nm波段范围内，光谱反射率值差异比较显著；而在可见光部分，对不同土壤有机质含量的区分比较难，差异性较弱。

2.2光谱指数与土壤有机质含量的相关性

为寻求基于分数阶微分构建的两波段光谱指数与土壤有机质含量之间的最佳阶数和波段信息，该研究分别分析了0～2阶次下（间隔0.2）构建的两波段光谱指数与土壤有机质含量之间的相关性，结果如图3所示。

分析发现，基于分数阶微分构建的NDVI、RVI和DVI均呈现极显著相关；其中NDVI和RVI指数相关系数均达到±0.8；而DVI指数相关性略低于前两种植被和指数。说明基于分数阶微分处理的光谱反射率构建NDVI和RVI对土壤有机质含量的敏感性明显增强。

为构建估算模型的参数筛选，该研究对相关系数阈值划分，划分标准为相关系数满足|r|≥0.80且通过0.01显著性水平检验的所有波段数量，见表3所示。通过相关性系数的统计分析发现，构建的DVI指数与土壤有机质含量之间的最高相关系数绝对值为0.79，主要是在0.0到1.0阶次范围内出现；而构建的NDVI和RVI指数在0.0到1.0阶次范围内出现了最高相关性，相关系数绝对值均为0.82，在原数据（0.0阶次）构建的NDVI指数满足|r|≥0.80的系数数量为82，RVI指数满足|r|≥0.80的系数数量为85；基于0.2阶次构建的NDVI和RVI指数满足|r|≥0.80的系数数量分别为32和33；在0.4到2.0阶次范围中，三种光谱指数均未出现满足|r|≥0.80的系数。

因此，该研究试着建立基于满足|r|≥0.80的系数对应波段反射率的土壤有机质含量估算模型并进行精度验证。

2.3基于CARS的敏感参数选择

为了验证模型变量共线性光谱指数的存在，该研究首先利用Pearson相关性方法筛选满足|r|≥0.80且通过0.01显著性水平检验的所有光谱指数的数量，再通过CARS（Competitive Adaptive Reweighted）算法对筛选的结果进一步验证。

由CARS算法进行验证并有效寻出最优变量组合中，设置采样次数为100次，误差值最小对应变量作为最佳参数集，结果如图4所示。

NDVI和RVI的对比各次采样RMSECV值均呈现随着迭代次数的增加而上升趋势，最小值分别是1.47g/kg、1.48g/kg、1.21g/kg和1.18g/kg；说明基于0.0和0.2阶次筛选出来的敏感光谱指数（NDVI和RVI）中，不存在共线性变量，符合建立土壤有机质含量估算模型参数。

2.4模型建立与验证

在土壤有机质含量与两波段植被指数之间的关联程度分析发现，基于分数阶微分的光谱指数对其相关程度具有一定的差异。其中，基于分数阶微分（0.0和0.2阶次）的NDVI和RVI两波段光谱指数优化后的关联程度呈现最高。在数据建模中，因0.4～2.0阶次中未出现满足|r|≥0.80且通过0.01显著性水平的光谱指数，因此不参与模型构建；而对0.0和0.2阶次构建的光谱指数选用3种机器学习算法（KNN、SVR、ANN）进行训练，并根据模型评价指标进行对比分析，训练数据集与验证数据集的模型评价结果见表4所示。

从0.0和0.2阶次构建的12种估算模型结果分析发现，基于原始光谱数据筛选的敏感参数比基于分数阶微分处理筛选结果2倍多，该研究利用分数阶微分方法对模型有效参数的筛选具有一定的贡献。其中，基于0.2阶微分光谱指数的建模精度R2从0.61提升到0.75，对模型的估算精度有所提高。从数据模拟与估算能力分析发现，KNN和SVR算法在不同数据建模效果与估算能力中均处于较好的运算和模拟过程，仅有该两种算法的相对分析误差RPD值分别达到了2.23、2.02、2.15，其余算法的相对分析误差RPD值均低于2.0。

通过该研究估算模型的验证值与估算值之间散点分布分析发现（图5），结合高光谱数据的分数阶微分预处理和3种机器学习算法的建模与模拟，对土壤有机质含量估算能力较好的阶数和机器学习方法分别为0.2阶、KNN算法；该研究基于0.2阶NDVI指数的K近邻算法模拟土壤有机质含量能力表现最佳，R²=0.73，RMSE=2.11g/kg，RPD=2.23。

基于0.2阶的高光谱数据处理，并计算了0.2阶数据下的NDVI指数，通过对指数的筛选，确定了参与模型的有效指数，在0.2阶处理数据中，参与光谱指数计算的有效组合波段如表5所示。

3讨论

分析基于分数阶微分预处理的光谱反射率与土壤有机质含量之间的关系，该研究以新疆乌鲁木齐县安宁渠镇土壤为数据源，采用分数阶微分处理方法对高光谱数据进行0.0～2.0阶次预处理，并运算两波段光谱指数（DVI、NDVI、RVI），筛选光谱指数与土壤有机质含量之间满足|r|≥0.80系数的敏感光谱指数，利用人工神经网络、K近邻和支持向量回归等3种建模方法，构建了基于分数阶微分和机器学习方法的土壤有机质含量估算模型，取得了较好的预测效果。该研究最后参与建模的敏感参数为原数据（0.0阶）和0.2阶的光谱数据，分析发现基于0.2阶的光谱指数（NDVI和RVI）模型精度较高。

已研究中，对光谱指数的计算多数基于特定波长反射率或显著性波段，对400～2400nm光谱数据来说，无法呈现光谱的隐含信息。徐继刚等研究学者表明光谱数据通过分数阶微分预处理不仅可以有效地减少背景噪声，而且突出隐含细节的光谱信息［23］。土壤光谱反射特性是因土壤各种理化性状相互作用产生，并具有一定的区域独特性和地域性。因此，在土壤光谱反射率数据的进一步研究上具有很大的意义［3032］。不同参数的高光谱建模研究中，高光谱原始数据或基于原始数据计算的传统植被指数、以及基于不同数学方法预处理等都是高光谱建模过程的重要组成部分，植被指数的构建要比单波段反射率的特性稳定且敏感性较强，整数阶预处理对光谱隐藏信息的突出具有很好的帮助，分数阶微分更能够细化和呈现隐藏光谱信息，对土壤不同参数的敏感性更显著。本研究采用全波段光谱数据的分数阶微分方法的归一化处理，分别运算基于原数据和处理后的光谱指数，寻求全波段有效信息的组合，降低了基线漂移和背景噪声的影响，增强了土壤有机质光谱吸收特征。

该研究综合不同预处理方法的优点，基于分数阶微分全波段预处理，进行所有可能两波段组合计算植被指数，结合机器学习的方法构建土壤有机质含量高光谱估算模型，对干旱区土壤参数高精度遥感监测方面提供了理论基础和科学依据。

4结论

以新疆乌鲁木齐县安宁渠镇土壤为数据源，采用分数阶微分处理方法对高光谱数据进行预处理，利用人工神经网络、K近邻和支持向量回归等3种建模方法和两波段光谱指数，构建了基于分数阶微分和机器学习方法的土壤有机质含量估算模型，得出了以下结论。

1）  在0～2阶次下（间隔0.2）构建的两波段光谱指数与土壤有机质含量之间的相关性中，得出基于分数阶微分构建的NDVI、RVI和DVI均呈现极显著相关；其中NDVI和RVI指数相关系数均达到了0.8以上；对DVI指数而言，NDVI和RVI对土壤有机质含量的敏感性明显较强。

2）  在相关系数满足|r|≥0.80且通过0.01显著性水平检验的所有波段数量分析中，原數据（0.0阶次）构建的NDVI、RVI指数满足|r|≥0.80的系数数量分别为82、85；而基于0.2阶次构建的NDVI和RVI指数满足|r|≥0.80的系数数量分别为32和33；有效的降低了参与模型的参数数量。

3）  对于土壤有机质含量估测模型的建立，3种机器学习算法的建模与模拟，对土壤有机质含量估算能力较好的阶数和机器学习方法分别为0.2阶、KNN算法；该研究基于0.2阶NDVI指数的K近邻算法模拟土壤有机质含量能力表现最佳，估算模型精度分别为R²=0.73，RMSE=2.11g/kg，RPD=2.23。

参考文献

［1］郑建乐， 张家祯， 刘微， 等. 土壤有机质含量高光谱定量反演研究［J］. 北方园艺， 2022（16）： 83-91.Zheng Jianle， Zhang Jiazhen， Liu Wei， et al. Study on quantitative inversion of soil organic matter content by hyperspectral ［J］. Northern Horticulture， 2022（16）： 83-91.

［2］成永生， 周瑶. 土壤重金属高光谱遥感定量监测研究进展与趋势［J］. 中国有色金属学报， 2021， 31（11）： 3450-3467.Cheng Yongsheng， Zhou Yao. Research progress and trend of quantitative monitoring of hyperspectral remote sensing for heavy metals in soil ［J］. The Chinese Journal of Nonferrous Metals. 2021， 31（11）： 3450-3467.

［3］焦彩霞， 郑光辉， 解宪丽， 等. 可见—短近红外成像光谱数据的土壤有机质含量估算［J］. 光谱学与光谱分析， 2020， 40（10）： 3277-3281.Jiao Caixia， Zheng Guanghui， Jie Xianli， et al. Prediction of soil organic matter using visible-short near-infrared imaging spectroscopy ［J］. Spectroscopy and Spectral Analysis， 2020， 40（10）： 3277-3281.

［4］赵瑞， 崔希民， 刘超. GF-5高光谱遥感影像的土壤有机质含量反演估算研究［J］. 中国环境科学， 2020， 40（8）： 3539-3545.Zhao Rui， Cui Ximin， Liu Chao. Inversion estimation of soil organic matter content based on GF-5 hyperspectral remote sensing image ［J］. China Environmental Science， 2020， 40（8）： 3539-3545.

［5］冯泉霖， 李洪涛， 徐夕博， 等. 基于聚类深度网络模型的莱州湾近岸平原表层土壤有机质含量遥感估算［J］. 安全与环境学报， 2022， 22（4）： 2248-2258.Feng Quanlin， Li Hongtao， Xu Xibo， et al. Remote sensed estimation of soil organic matter using cluster-based deep neural network in the nearshore plains of Laizhou Bay， eastern China ［J］. Journal of Safety and Environment， 2022， 22（4）： 2248-2258.

［6］葉勤， 姜雪芹， 李西灿， 等. 基于高光谱数据的土壤有机质含量反演模型比较［J］. 农业机械学报， 2017， 48（3）： 164-172.Ye Qin， Jiang Xueqin， Li Xishan， et al. Comparison on inversion model of soil organic matter content based on hyperspectral data ［J］. Transactions of the Chinese Society for Agricultural Machinery， 2017， 48（3）： 164-172.

［7］王延仓， 杨贵军， 朱金山， 等. 基于小波变换与偏最小二乘耦合模型估测北方潮土有机质含量［J］. 光谱学与光谱分析， 2014， 34（7）： 1922-1926.Wang Yancang， Ynag Guijun， Zhu Jinshan， et al. Estimation of organic matter content of north Fluvo-aquic soil based on the coupling model of wavelet transform and partial least squares ［J］. Spectroscopy and Spectral Analysis， 2014， 34（7）： 1922-1926.

［7］于雷， 洪永胜， 耿雷， 等. 基于偏最小二乘回归的土壤有机质含量高光谱估算［J］. 农业工程学报， 2015， 31（14）： 103-109.Yu Lei， Hong Yongsheng， Geng Lei， et al. Hyperspectral estimation of soil organic matter content based on partial least squares regression ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2015， 31（14）： 103-109.

［8］Krishnan P， Alexander J D， Butler B J， et al. Reflectance technique for predicting soil organic matter ［J］. Soil Science Society of America Journal， 1980， 44（6）： 1282-1285.

［9］Hummel J W， Sudduth K A， Hollinger S E. Soil moisture and organic matter prediction of surface and subsurface soils using an NIR soil sensor ［J］. Computers and Electronics in Agriculture， 2001， 32（2）： 149-165.

［10］Conforti M， Buttafuoco G， Leone A P， et al. Studying the relationship between water-induced soil erosion and soil organic matter using Vis-NIR spectroscopy and geomorphological analysis： A case study in southern Italy ［J］. Catena， 2013， 110： 44-58.

［11］尚天浩， 毛鸿欣， 张俊华， 等. 基于PCA敏感波段筛选与SVM建模的银川平原土壤有机质高光谱估算［J］. 生态学杂志， 2021， 40（12）： 4128-4136.Shang Tianhao， Mao Hongxin， Zhang Junhua， et al. Hyperspctral estimation of soil organic matter content in Yinchuan plain， China based on PCA sensitive band screening and SVM modeling ［J］. Chinese Journal of Ecology， 2021， 40（12）： 4128-4136.

［12］何少芳， 沈陆明， 谢红霞. 生成式对抗网络的土壤有机质高光谱估测模型［J］. 光谱学与光谱分析， 2021， 41（6）： 1905-1911.He Shaofang， Shen Luming， Xie Hongxia. Hyperspectral estimation model of soil organic matter content using generative adversarial networks ［J］. Spectroscopy and Spectral Analysis， 2021， 41（6）： 1905-1911.

［13］尼加提·卡斯木， 茹克亚·萨吾提， 师庆东， 等. 基于优化光谱指数的土壤有机质含量估算［J］. 农业机械学报， 2018， 49（11）： 155-163.Nejat Kasim， Rukeya Sawut， Shi Qingdong， et al. Estimation of soil organic matter content based on optimized spectral index ［J］. Transactions of the Chinese Society for Agricultural Machinery，  2018， 49（11）： 155-163.

［14］栾福明， 张小雷， 熊黑钢， 等. 基于不同模型的土壤有机質含量高光谱反演比较分析［J］. 光谱学与光谱分析， 2013， 33（1）： 196-200.Luan Fuming， Zhang Xiaolei， Xiong Heigang， et al. Comparative analysis of soil organic matter content based on different hyperspectral inversion models ［J］. Spectroscopy and Spectral Analysis， 2013， 33（1）： 196-200.

［15］刘磊， 沈润平， 丁国香. 基于高光谱的土壤有机质含量估算研究［J］. 光谱学与光谱分析， 2011， 31（3）： 762-766.Liu Lei， Shen Runping， Ding Guoxiang. Studies on the estimation of soil organic matter content based on hyper-spectrum ［J］. Spectroscopy and Spectral Analysis， 2011， 31（3）： 762-766.

［16］李晓明， 韩霁昌， 李娟. 典型半干旱区土壤盐分高光谱特征反演［J］. 光谱学与光谱分析， 2014， 34（4）： 1081-1084.Li Xiaoming， Han Jichang， Li Juan. Research on hyperspectral inversion of soil salinity in typical semiarid area ［J］. Spectroscopy and Spectral Analysis， 2014， 34（4）： 1081-1084.

［17］胡慧玲， 玉素甫·艾力， 阿布力米提·阿布都卡德尔. 乌鲁木齐市安宁渠区蔬菜中重金属的分布特征研究［J］. 新疆大学学报（自然科学版）， 2003， 20（3）： 260-263.Hu Huiling， Yusup Ali， Abdumijit Abdukadir. Study on distribution characterastics of heavy metals in vegetables of Anningqu district in Urumqi ［J］. Journal of Xinjiang University （Natural Science Edition）， 2003， 20（3）： 260-263.

［18］米热阿地力·库尔班， 买合木提·巴拉提， 斯马伊力江·艾尼瓦尔， 等. 乌鲁木齐市安宁渠蔬菜基地土壤重金属污染现状及潜在生态风险评价［J］. 地球与环境， 2019， 47（4）： 485-494.Miradil Kurban， Maihemut Balati， Simayil Ainiwar， et al. Characteristics and ecological risk assessment of heavy metals in soil of the Anningqu vegetable base in Urumqi ［J］. Earth and Environment， 2019， 47（4）： 485-494.

［19］许月英， 李刚， 贾那别克. 乌鲁木齐“市菜篮子”基地土壤环境质量现状调查［J］. 干旱环境监测， 2006（3）： 137-141.Xu Yueying， Li Gang， Jianabieke. Investigation on the soil environmental quality of “Shopping Basket” base in Urumqi ［J］. Arid Environmental Monitoring， 2006（3）： 137-141.

［20］杜萍萍， 何丽， 王亚宇. 乌鲁木齐市蔬菜基地土壤有效态镉的空间变异特征［J］. 干旱环境监测， 2011， 25（2）： 85-89.Du Pingping， He Li， Wang Yayu. Spatial variation of soil available Cd in Urumqi vegetable base ［J］. Arid Environmental Monitoring， 2011， 25（2）： 85-89.

［21］李孝兰. 用重铬酸钾氧化容量法测定土壤有机质关键技术［J］. 现代农村科技， 2013（23）： 36.

［22］林世敏， 许传炬. 分数阶微分方程的理论和数值方法研究［J］. 计算数学， 2016， 38（1）： 1-24.Li Shimin， Xu Chuanju. Theoretical and numerical investigation of fractional differential equations ［J］. Mathematica Numerica Sinica， 2016， 38（1）：  1-24.

［23］徐继刚， 冯新泸， 管亮， 等. 分数阶微分在红外光谱数据预处理中的应用［J］. 化工自动化及仪表， 2012（3）： 347-351.Xu Jigang， Feng Xinlu， Guang Liang， et al. Fractional differential application in reprocessing infrared spectral data ［J］. Control and Instruments in Chemical Industry， 2012（3）： 347-351.

［24］高琪， 王玉珍， 冯春晖， 等. 基于改进型光谱指数的荒漠土壤水分遥感反演［J］. 国土资源遥感， 2022（1）： 142-150.Gao Qi， Wand Yuzhen， Feng Chunhui， et al. Remote sensing inversion of desert soil moisture based on improved spectral indices ［J］. Remote Sensing for Natural Resources， 2022（1）： 142-150.

［25］姚付启， 张振华， 杨润亚， 等. 基于红边参数的植被叶绿素含量高光谱估算模型［J］. 农业工程学报， 2009， 25（13）： 123-129.Yao Fuqi， Zhang Zhenhua， Yang Runya， et al. Hyperspectral models for estimating vegetation chlorophyll content based on red edge parameter ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2009， 25（13）： 123-129.

［26］唐海涛， 孟祥添， 苏循新， 等. 基于CARS算法的不同类型土壤有机质高光谱预测［J］. 农业工程学报， 2021， 37（2）： 105-113.Tang Haitao， Meng Xiangtian， Su Xunxin， et al. Hyperspectral prediction on soil organic matter of different types using CARS algorithm ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2021， 37（2）： 105-113.

［27］王喆， 连炎清， 李晓娜， 等. 基于机器学习的浐灞河水质参数遥感反演研究［J］. 人民长江， 2022， 53（9）： 13-18.Wang Zhe， Lian Yanqing， Li Xiaona， et al. Research on remote sensing inversion of water quality parameters in Chanhe River and Bahe River based on machine learning ［J］. Yangtze River， 2022， 53（9）： 13-18.

［28］王新颖， 隽志才， 吴庆妍， 等. KNN算法的数据优化策略［J］. 吉林大学学报（信息科学版）， 2010， 28（3）： 309-313.Wang Xinying， Jun Zhicai， Wu Qingyan， et al. Data optimization strategy of KNN algorithm ［J］. Journal of Jilin University （Information Science Edition）， 2010， 28（3）： 309-313.

［29］鄭立华， 李民赞， 安晓飞， 等. 基于近红外光谱和支持向量机的土壤参数预测［J］. 农业工程学报， 2010， 26（S2）： 81-87.Zheng Lihua， Li Minzan， An Xiaofei， et al. Forecasting soil parameters based on NIR and SVM ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2010， 26（S2）： 81-87.

［30］郑淼， 王翔， 李思佳， 等. 黑土区土壤有机质和全氮含量遥感反演研究［J］. 地理科学， 2022， 42（8）： 1336-1347.Zheng Miao， Wnag Xiang， Li Sijia， et al. Remote sensing inversion of soil organic matter and total nitrogen in black soil region ［J］. Scientia Geographica Sinica， 2022， 42（8）： 1336-1347.

［32］马媛. 干旱区土壤肥力变异规律研究——以阜康地区为例［D］. 乌鲁木齐： 新疆大学， 2004.Ma Yuan. Study on variation patterns of soil fertility in arid regions： A case study of Fukang region ［D］. Urumqi： Xinjiang University， 2004.