灌水技术参数对波涌灌间歇入渗特性优化研究

薛桦　张晓斌　傅渝亮　何振嘉

摘要：為定量评价波涌灌间歇入渗中灌水技术参数及交互作用对间歇入渗减渗作用的影响，通过室内土柱入渗试验，进行地下水浅埋下间歇入渗试验，以累积入渗量和减渗率作为试验指标，通过两种方法（偏最小二乘法和逐步选择法）对循环率、周期供水时间以及周期数3因素进行回归分析，并建立线性回归方程，对方程及其各因素进行方差分析。采用响应优化分析法对回归模型进行指标优化。试验结果表明：所建回归方程线性相关性较好，其决定系数R2大于0.97，误差平方和SSE小于1.1，较好地反应各单因素及其交互作用下的入渗指标。与偏最小二乘法相比，逐步选择法可满足较高精度要求，当周期数为3、周期供水时间为30min、间歇入渗循环率为1/4时，入渗量为6.29cm，减渗率为19.15%，标准误差值均小于0.01，合意值均达0.8以上。为波涌灌灌水技术进一步研究奠定科学基础。

关键词：波涌灌间歇入渗；入渗特性；多因素分析；偏最小二乘法；逐步选择法

中图分类号：S275.8文献标识码：A文章编号：20955553 （2023） 11018408

Study on optimization of intermittent infiltration characteristics of surge irrigation by

irrigation technical parameters

Xue Hua Zhang XiaobinFu Yuliang He Zhenjia

（1. Shanxi Water Conservancy Vocational and Technical College， Yuncheng， 044000， China; 2. Yuncheng University，

Yuncheng， 044000， China;  3. School of Water Conservancy， North China University of Water Resources and Electric

Power， Zhengzhou， 450045; 4. Shaanxi Provincial Land Engineering Construction Group Co.， Ltd.， Xian， 710075， China）

Abstract：In order to quantitatively evaluate the influence of the irrigation technology parameters and their related interactive factors on the reduced infiltration effect of the intermittent infiltration， intermittent infiltration tests were carried out in shallow groundwater through the indoor soil infiltration tests. The accumulated infiltration amount and the reduced infiltration rate were taken as the experimental indices. At the same time， two methods （Partial Least Square method and stepwise selection method） were applied by the software of Minitab to take the regression analysis of three factors， which included the cycle rate， the cycle time of water and the number of cycles， the linear regression equation was established， and the variance analysis was conducted to the equations and the factors. The experimental results showed that the linear correlation of the regression equation was good， the coefficient of determination R2 was greater than 0.97， and the sum of error squares SSE was less than 1.1， which reflected the infiltration index of each single factor and its interaction well. Compared with PLSR， the stepwise selection method can meet the requirements of high precision. When the number of cycles is 3， the periodic water supply time is 30 min， and the intermittent infiltration cycle rate is 1/4， the infiltration volume is 6.29 cm， the seepage reduction rate is 19.15%， the standard error values are less than 0.01， and the consensus values are above 0.8. It lays a scientific foundation for the further study of surge irrigation water technology.

Keywords：intermittent surge irrigation infiltration; infiltration characteristics; multi-factor analysis; PLSR; stepwise selection method

0引言

灌水技术参数的选取直接影响波涌灌间歇入渗的减渗效果［12］。特别是当地下水浅埋较高时，由于长期施用化肥加之农业用水浪费，土壤水深层渗漏的问题尤为突出［35］。因此，如何优化间歇入渗灌水技术参数，既能在计划湿润层保持较高水分供给作物根系对水分的吸收，又能减小深层渗漏的发生，是当前亟待解决的问题。

偏最小二乘法是一种用于回归分析的统计方法，与主成分分析（PCA）类似，可以有效提高回归模型的稳定性和精度，也用来解决特征过多、共线性过高的问题，也可以用来降维。主要应用于化学、生物、医学等领域［6］，用来分析光谱数据［7］、基因表达数据［8］、药物筛选数据［9］等，一般用来评估变量的重要性和选择最优的变量子集。而最优子集法是一种用于筛选变量的方法，可以从多个变量中选择最佳模型，其基本思想是尝试所有可能的变量组合，然后选择最佳的模型，模型所包含的变量就是筛选出来的最优变量，这种方法可以应用于任何需要从多个变量中选择最佳模型的领域，常见于金融［10］、生物学［11］、工程［12］等。

波涌灌的周期性供水特性决定了其灌溉水分入渗过程的间歇性，合理的波涌灌间歇入渗灌水技术要素组合决定了波涌灌的减渗能力和灌水质量［13］。波涌灌灌水技术特性参数主要的影响因素有循环率、周期数和周期供水时间，采用多种方法优化灌水技术参数一直是国内外对波涌灌灌水技术要素的主要研究内容。目前，波涌灌灌水技术相关研究内容主要集中在间歇入渗模型［1418］、间歇入渗特性［1924］、水流运动特性［2526］和机理性研究［17， 27］，以及波涌灌溉适应性、灌溉实施方案和灌溉效益分析方面［2829］。非饱和土壤条件下波涌灌间歇入渗对循环率、周期数、周期供水时间等因素的单个效应研究已取得大量研究成果，而系统地讨论地下水浅埋影响下各灌水技术因素在间歇入渗过程中交互效应的工作未见相关资料。

因此，本文通过实验室模拟和统计优化的方法相结合，研究了地下水浅埋影响条件下波涌灌间歇入渗灌水技术参数的优化方案，采用偏最小二乘法（Partial Least Squares Regression，PLSR）［30］和最优子集法（Best Subset Selection Regression，BSSR）［31］实现优化。利用Minitab对其进行灌水技术参数多因素变化室内土柱入渗试验，因Minitab软件［32］内嵌的最小二乘法和最优子集法模块，可分别对地下水影响条件下波涌灌间歇入渗灌水技术参数优化进行研究和对比，并以3个循环率、2个周期数和2周期供水时间作为间歇入渗灌水影响因素，以相同净入渗时间连续入渗作对比试验，进行多因素组合下的室内一维垂直间歇入渗供水试验。通过对试验数据进行回归分析，讨论在间歇入渗条件下的入渗量和减渗率两方面是否存在循环率、周期数和周期供水时间的二阶交互效应及影响效果，并尝试在试验参数取值范围内，利用回归模型寻优最佳灌水技术参数。

1材料与方法

1.1试验装置与方法

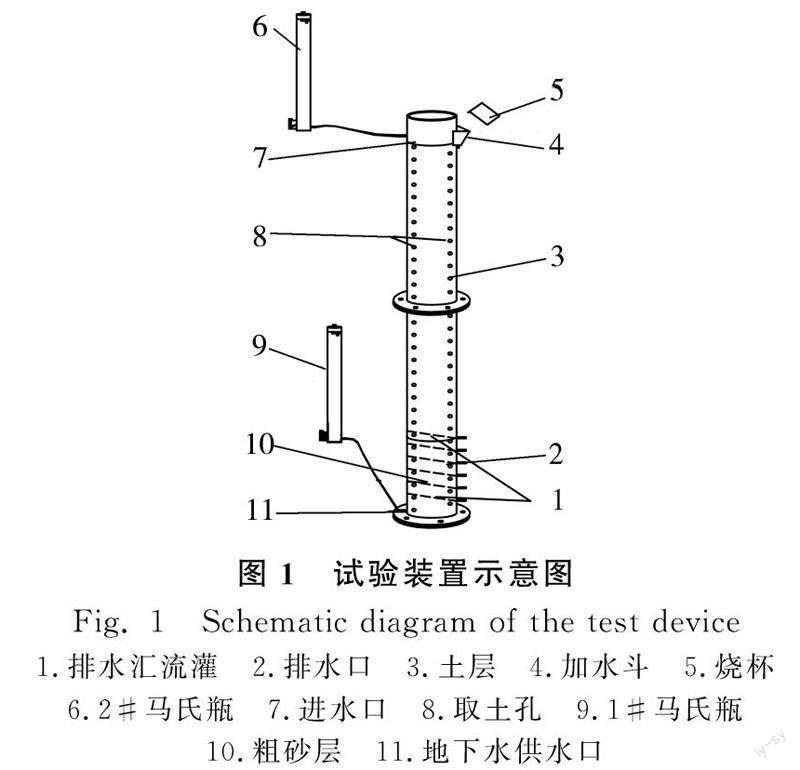
试验在西安理工大学西北水资源与环境生态教育部重点实验室进行，采用间歇入渗设备进行灌水试验，并观测地下水影响条件下间歇供水入渗量及土壤水分动态指标。试验装置由土柱，地下水控制系统和入渗供水系统组成，见图1所示。

11.地下水供水口

试验土柱为高210.0cm、内径21.4cm的有机玻璃柱；底部为粒径3.0～7.0mm砂砾石组成的地下饱和含水层，深度为60.0cm；上部为土壤粒径小于2.0mm粉土模拟150.0cm深度的非饱和土壤层。垂直入渗时，为防止上层土壤进入底部饱和含水层，中间由滤纸隔断，沿土柱垂向梅花状布设取土孔，每列孔径为2.0cm、间隔5.0cm。土柱顶部设加水斗，供水时防止水流冲击破坏表层土壤的致密层，间歇停水时及时排空土柱表面积水。入渗时，采用2.5cm定压力水头控制。地下水由1#马氏瓶控制系统；入渗供水由马氏瓶2#与土柱上部供水口连接组成，通过固定马氏瓶进气孔的高度调控定水头供水［3334］。

试验土壤采用西安粉土，土壤颗粒分析使用英国的Mastersizer-2000型激光粒度仪测定，颗粒组成如表1所示。

土样基本理化性质为：土样经过风干、碾压、过筛、配水得到试验土样，按容重1.30g/cm3、每隔5.0cm一层分层填装；初始饱和导水率按设定的土壤容重装入南-55渗透仪，并按常水头法测定，初始飽和导水率Ks为0.023cm/min；入渗过程中，入渗量通过马氏瓶进行控制和计量，单位cm；减渗率可以衡量间歇入渗量相较连续入渗量减小的程度指标，采用η表示，初始含水率为土壤体积含水率，采用θ0表示，质量含水率采用烘干法进行测定，饱和含水率为设定容重下测定饱和导水率条件下的体积含水率，采用θs表示，θ0和θs分别为0.014cm3/cm3、0.454cm3/cm3；土壤pH值采用定性pH试纸测定，pH值为7.50。试验过程用水为蒸馏水。

为便于将连续入渗与间歇入渗进行对比，减渗率值如式（1）所示。

η=I_b－I₀/I_b×100%（1）

式中：

η——间歇入渗的减渗率，%；

I_b——

相同条件、同时段的连续入渗的累积入渗量，cm；

I₀——

相同条件、同时段的间歇入渗的累积入渗量，cm。

1.2试验方案

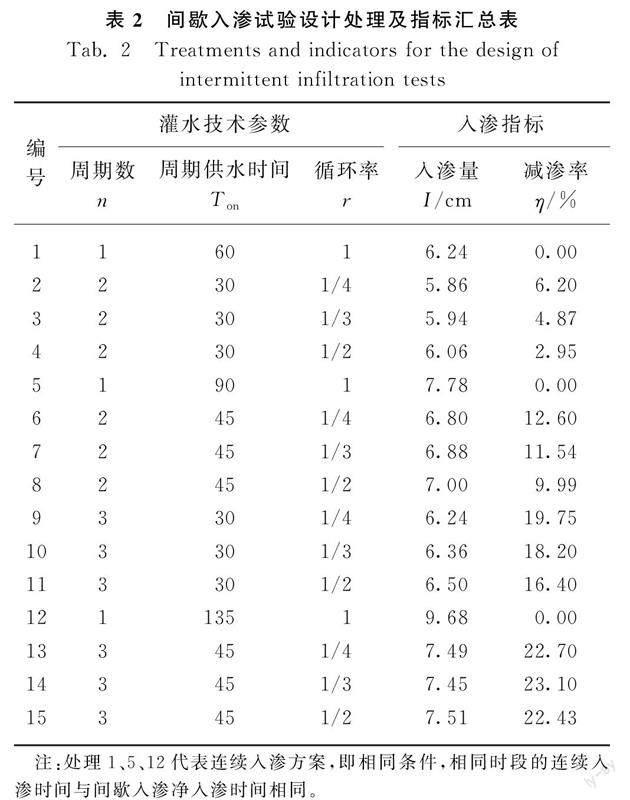
试验采用均匀设计试验数据的处理方法，灌水技术参数为3因素水平，分别是周期数n、周期供水时间Ton和循环率r。周期数设置2水平（n=2、3），周期用水时间设置2水平（Ton=30min、45min），循环率设置3水平（r=1/2、1/3、1/4），均有相同净入渗时间连续入渗作对比处理，计算减渗率。共计15个处理，每个处理3个重复，以累积入渗量和减渗率平均值作为最终指标。

1.3试验分析方法

通过对试验参数及响应（入渗量、减渗率）实测值进行实际观测处理的基础上，建立多元回归方程拟合因素与响应值之间的函数关系，并对回归模型的入渗指标效应进行了综合评价，最后在给定的参数范围内得到最佳因素组合，确定响应优化值［35］。具体方法步骤如下：首先，不同处理方案的室内一维垂直间歇入渗试验得出实际入渗量和对应处理下的减渗率；其次，利用各因素水平和响应指标（入渗量，减渗率）作为变量值和响应值，采用偏最小二乘法和逐步选择法分别建立多因素线性回归方程，并对实际线性回归方程进行标准化；再根据各因素系数大小对响应指标进行效应大小顺序判断，对回归方程误差分析以及精度分析；最后，在所得室内试验结果的基础上，对已有的灌水技术参数取值范围内，设定预测响应目标选用回归精度较高的模型进行响应优化分析，得到该预测目标下的最优参数值。并对最优参数下的入渗指标进行可靠性检验。

2结果与分析

运用Minitab数据统计分析软件，采用响应优化分析法进行方案确定［36］。具体设计方案结果见表2。

2.1PLSR回归模型的建立及精度检验

根据偏最小二乘法（PLSR）的建模原理和方法，利用Minitab数据处理软件对12组间歇入渗实测结果进行处理并建立线性回归数学模型。入渗量和减渗率回归模型见式（2）和式（3）。

入渗量模型

I=3.50+1.43r+0.004n+0.05T_on+0.01n×T_on+0.09n×r－0.03T_on×r（2）

减渗率模型

η=－29.16－40.35r+15.60n+0.55T_on－0.14n×T_on+5.30n×r+0.47T_on×r（3）

式中：

n×T_on、n×r、T_on×r——二阶交互因素。

由于各因素之间的计量单位和数量级不尽相同，因而使得各因素之间不能进行有效综合分析，故在假定变量服从正态分布的前提下，将回归方程变量值转化为数学期望为0，方差为1的标准化数值，从而达到同度量效应。标准化后结果如式（4）和式（5）所示。

标准化入渗量模型

I_s=0.26r+0.004n+0.61T_on+0.57n×T_on+0.05n×r－0.22T_on×r（4）

标准化减渗率模型

η_s=－0.61r+1.13n+0.59T_on－0.53n×T_on+0.24n×r+0.33T_on×r（5）

式中：

I_s和η_s——

标准化后的Iη。

为评价所建立模型的回归效果，以误差平方和SSE、决定系数R²和Press（predicted residual sum of squares）残差值及方差分析作为模型精度的检验指标，对上述方程进行计算获得各评价指标结果见表3。

可以看出，入渗量方程的F_I=399.71，P=0.000 1<0.001，减渗率方程的F_η=643.03，且P=0.000 1<0.001，交互作用下的线性回归模型均达到极显著水平。从标准化回归方程系数影响效应来看，各因素对入渗量影响效应为：周期供水时间>周期数×周期供水时间>循环率>周期供水时间×循环率>周期数×循环率>周期数；其中周期供水时间与循环率交互作用对入渗量产生负效应，其他因素对入渗量产生正效应；交互作用下各因素对减渗率影响效应为：周期数>循环率>周期供水时间>周期供水时间×周期数>周期供水时间×循环率>周期数×循环率。其中，周期数×周期供水时间和循環率均对减渗率产生负效应，其他因素均对减渗率产生正效应。

2.2BSSR逐步选择回归模型的建立及精度检验

根据逐步选择回归分析的建模原理和方法，利用Minitab最优子集法模块逐步选择法建立线性回归数学模型，入渗量和减渗率数学模型如式（6）、式（7）所示。

入渗量模型

I′=3.68+0.687r+0.07n+0.04T_on+0.01n×T_on（6）

减渗率模型

η′=-40.58－9.37r+17.61n+0.73T_on－0.14n×T_on（7）

其对应的标准化模型如式（8）、式（9）所示。

标准化入渗量模型

I′_s=0.12r+0.89n+0.43T_on+0.08n×T_on（8）

标准化减渗率模型

η′_s=-0.14r+0.90n+0.41T_on－0.08n×T_on（9）

为评价所建立模型的回归效果，以误差平方和SSE、决定系数R²和Press残差以及方差分析作为模型精度的检验指标，对上述方程计算获得各评价指标结果见表4。

可以看出，入渗量回归方程的F_I′=428.62，P=0.000 1<0.001，减渗率回归方程的F_η′=711.88，且P=0.000 1<0.001，回归方程均达到极显著水平。

进一步对回归方程中的系数进行T检验，选用α=0.05判别是否差异性显著。检验结果见表5。通过检验结果可以看出，在α=0.05显著水平下，拒绝原假设，各回归系数均不为0，说明除了3因素各自对入渗指标有显著性影响外，周期数×周期供水时间的交互效应也对入渗指标的变化产生了显著性影响，并且从方差膨胀因子（VIF值）中可以得出：0

从式（8）、式（9）得到，各因素对2入渗指标影响效应一致，影响效应顺序为：周期数>周期供水时间>循环率>周期数×周期供水时间，其中，循环率与周期供水时间×周期数均对减渗率产生负效应影响，其他因素均产生正效应影响。

2.3比较模型分析结果

从表5可以看出，上述2种回归法VIF值均小于10，避免自变量数据之间可能出现的多重共线性情况，并且通过假设检验和方差分析两种方法建立的回归方程及各项系数均具有统计学意义。标准化后的模型各项系数对入渗指标影响程度不尽相同。在交互作用下，PLSR法3因素的标准化系数对入渗量影响效应为：周期供水时间、循环率、周期数；逐步选择法3因素的标准化系数对入渗量影响效应为：周期数、周期供水时间、循环率，其二阶交互因素的标准化系数对入渗量影响效应较PLSR法较逐步选择法方程系数项少，二阶交互因素仅有周期数×周期供水时间对回归模型产生效应。

减渗率回归模型采用的两种方法所得的标准化系数的影响效应也不尽相同，在交互作用下，PLSR法单因素的标准化系数对减渗率影响效应顺序为：周期数>循环率>周期供水时间；逐步选择法单因素的标准化系数对减渗率影响效应顺序为：周期数>周期供水时间>循环率。同时还可以看出，PLSR法二阶交互因素对减渗率指标有显著性影响，逐步选择法仅周期数×周期供水时间对减渗率有显著性影响。

一般地，线性回归方程参数越多，回归效果越好，精度越高。通过以上两种方法对比，在不影响回归方程精度的情况下，逐步选择法较PLSR法回归检验效果好，并且在减少回归方程系数项的前提下，逐步选择法的回归方程的精度检验效果较好。因此，本研究采用进一步对逐步选择法得回归模型进行响应优化分析。

2.4BSSR逐步選择法优化响应分析

对于波涌灌间歇入渗而言合适的灌水技术参数的选择使波涌灌溉具有节水、灌水均匀、深层渗漏小、灌水效率高等优点，因此基于试验参数取值范围内将已建的回归方程进行灌水技术参数寻优，本次优化目标拟入渗量最小，减渗率最大进行预设优化目标并进行参数寻优计算，计算结果如表6所示。

通过优化响应分析可得，在周期数n为3、周期供水时间为30min、循环率为1/4条件下，响应指标可满足最优响应值，即入渗量目标拟合值为6.29cm，减渗率目标拟合值为19.15%，优化响应后的累积入渗量标准误差值为0.044，减渗率标准误差值亦为0.092。优化响应后的意合值能够看出，对于满足入渗量和减渗率响应的优化结果程度较好，有效性较高，以方程预设值入渗量最小，减渗率大的合意值和复合合意值均达到了0.80以上。

另外，通过优化响应器可进一步检验预测值可靠性，利用优化响应分析得到参数结果与相同灌水技术参数条件下的5组重复处理实测值进行对比，对比结果如表7所示。

由表7可知，采用逐步选择分析法建立的模型进行优化所得灌水技术参数的入渗指标拟合值与实测试验重复数据结果的相对偏差均在±10%以内，吻合较好，这说明所建的模型能够较好地反应实际情况，优化结果可靠。该建模方法及模型是实用可行的。

3讨论

1）  波涌灌间歇入渗的减渗特性受周期性循环供水作用影响较大，特别是土壤质地相同条件下，灌水技术参数的改变，致使土壤表面的大量细部土-沙颗粒不断随水流波动发生扩散、碰撞、黏结、破碎、沉淀等不同的运动过程从而形成一层薄薄的致密层［37］，土壤表面致密层的形成也会因灌水技术参数的不同而影响水沙循环落淤等现象，最终土壤表面形成密实度不一的致密层。因此，致密层作为农田土壤水分运移和保持的影响因素，对其入渗能力的变化起到至关重要的作用。致密层密实度太大，导致田面水分无法补充到土壤里；致密层密实度太小，亦会使降低土壤耕层土壤水储水能力和水分供应能力，导致水分利用率不高。因此需要通过一定科学合理的方法优化灌水技术参数，讨论波涌灌间歇入渗多因素灌水技术参数变化对土壤入渗能力的影响是十分必要的。

2）  通过两种优化方法对技术参数优化结果可以看出，对波涌灌间歇入渗过程中的入渗量和减渗率影响结果较大（P<0.001）的主要因其周期数和供水时间以及两者之间的交互效应导致的。经计算，以供水周期90min为例，相同净入渗时间条件下间歇入渗较连续入渗节约用水量可达到76.5～153m³/hm²之间，其优化结果有助于减小垂直入渗水量，显著提高土壤水侧向渗透性和水分扩散速率［38］的作用。

3）  由于土壤水入渗能力的影响因素很多，不同因素对土壤水入渗能力的影响范围也各不相同。目前，对于波涌灌间歇供水条件下的土壤入渗特性及灌水技术参数的研究大多数都只针对单因素进行分析，而少数针对波涌灌间歇入渗特性以及灌水技术参数整体进行多因素分析的研究均采取控制单一变量法，忽略了各因素对间歇入渗特性的交互作用［29］。各灌水技术参数同时起作用的结果不是各参数分别作用的简单相加，各个灌水技术参数的结合会产生一个新的效应。生产实践中波涌灌间歇入渗特性是受诸多灌水技术参数交互影响，研究各参数对波涌灌间歇入渗特性的交互作用是必要的［39］。本文通过两种优化方法较好建立了多因素交互作用下的波涌灌间歇入渗灌水技术优化模型，以期深入了解各灌水技术参数对间歇入渗特性的交互作用，为确定波涌灌灌水技术要素最优组合提供理论依据。

4结论

1）  本文分别采用偏最小二乘法与最优子集逐步选择法建立了波涌灌间歇入渗中以循环率、周期数、周期供水时间为自变量，入渗量和减渗率为试验指标的间歇入渗优化模型。并且考虑了各因素之间的二阶交互作用，对比结果发现两种方法均能得到精度较高的线性回归方程。

2）  通过对回归方程进一步标准化，得到标准化系数，并进行影响效应分析，两种回归方法对各因素影响入渗能力的主次顺序不尽相同。

3）  通过对两种方法建立回归方程的方差分析与假设检验可以得出，与偏最小二乘法相比，逐步选择法在减少影响因子条件下的模型精度，回归模型依然满足较高精度要求。因此，令优化目标拟入渗量最小，减渗率最大条件下采用逐步选择法对回归模型进行参数响应优化。当周期数为3、周期供水时间为30min、间歇入渗循环率为1/4的情况下，得到预测响应入渗量为6.29cm，减渗率为19.15%。优化后的指标意合值和复合意合值均达到0.80以上，优化响应结果满意。

4）  采用优化后预测的参数和入渗指标进行室内入渗对比试验，并对优化结果进行可靠性验证，对比结果相对偏差均在±10%以内，优化结果可信。

参考文献

［1］陈琳， 费良军， 傅渝亮， 等. 地下水浅埋下层状土壤波涌畦灌间歇入渗模型研究［J］. 农业机械学报， 2018， 49（12）： 314-324.Chen Lin， Fei Liangjun， Fu Yuliang， et al. Intermittent infiltration model of surge border irrigation in layered soil under groundwater ［J］. Transactions of the Chinese Society for Agricultural Machinery， 2018， 49（12）： 314-324.

［2］傅渝亮， 费良军， 聂卫波， 等. 基于Green-Ampt和Philip模型的波涌灌间歇入渗模型研究［J］. 农业机械学报， 2016， 47（9）： 194-201.Fu Yuliang， Fei Liangjun， Nie Weibo， et al. Intermittentinfiltration of surge irrigation model research based on Green-Ampt and Philip models ［J］. Transactions of the Chinese Society for Agricultural Machinery， 2016， 47（9）： 194-201.

［3］Heydari N， Das Gupta A， Loof R. Salinity and sodicity influences on infiltration during surge flow irrigation ［J］. Irrigation Science， 2001， 20： 165-173.

［4］代志伟， 程曼， 袁洪波， 等. 温室灌溉控制策略研究进展［J］. 中国农机化学报， 2022， 43（9）： 63-72.Dai Zhiwei， Cheng Man， Yuan Hongbo， et al. Review of irrigation control strategy for greenhouse ［J］. Journal of Chinese Agricultural Mechanization， 2022， 43（9）： 63-72.

［5］任玉忠， 董新光， 吳彬， 等. 干旱区枣园土壤水分运动及深层渗漏数值模拟［J］. 节水灌溉， 2010（9）： 24-26.Ren Yuzhong， Dong Xinguang， Wu Bin， et al. Numerical simulation of soil water movement and deep seepage of jujube orchard in drought area ［J］. Water Saving Irrigation， 2010（9）： 24-26.

［6］Ju Suh Y， Finch S J， Mendell N R. Application of a Bayesian method for optimal subset regression to linkage analysis of Q1 and Q2 ［J］. Genetic Epidemiology， 2001， 21（S1）： S706-S711.

［7］陈凤霞， 杨天伟， 李杰庆， 等. 基于偏最小二乘法判别分析与随机森林算法的牛肝菌种类鉴别［J］. 光谱学与光谱分析， 2022， 42（2）： 549-554.Chen Fengxia， Yang Tianwei， Li Jieqing， et al. Identification of boletus species based on discriminant analysis of partial least squares and random forest algorithm ［J］. Spectroscopy and Spectral Analysis， 2022， 42（2）： 549-554.

［8］李建更， 李辉. 样条变换偏最小二乘在肝癌数据分类中的应用［J］. 生物学杂志， 2011， 28（6）： 58-61.Li Jiangeng， Li Hui. The classification of hepatocellular carcinoma data set with partial least squares base on spline transformation ［J］. Journal of Biology， 2011， 28（6）： 58-61.

［9］徐培平， 张奉学， 符林春， 等. 基于均匀设计—偏最小二乘回归建模的中药复方配伍规律研究方法［J］. 中草药， 2011， 42（4）： 819-824.Xu Peiping， Zhang Fenxue， Fu Linchun， et al. A mathematical method for analyzing compatibility law of Chinese herbal formula based on UD-PLS ［J］. Chinese Traditional and Herbal Drugs， 2011， 42（4）： 819-824.

［10］Hafayed M. Singular mean-field optimal control for forward-backward stochastic systems and applications to finance ［J］. International Journal of Dynamics and Control， 2014， 2： 542-554.

［11］Ramírez J C， Cura C I， da Cruz Moreira O， et al. Analytical validation of quantitative real-time PCR methods for quantification of Trypanosoma cruzi DNA in blood samples from Chagas disease patients ［J］. The Journal of Molecular Diagnostics， 2015， 17（5）： 605-615.

［12］Hoseinpour-Lonbar M， Alavi M Z， Palassi M. Selection of asphalt mix with optimal fracture properties at intermediate temperature using Taguchi method for design of experiment ［J］. Construction and Building Materials， 2020， 262： 120601.

［13］傅渝亮， 费良军， 聂卫波， 等. 波涌灌间歇入渗饱和-非饱和土壤水分运动数值模拟及试验［J］. 农业工程学报， 2015（2）： 66-71.Fu Yuliang， Fei Liangjun， Nie Weibo， et al. Numerical simulation and experiment of soil moisture movement in saturated-unsaturated soil under surge irrigation ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2015（2）： 66-71.

［14］高昌珍， 左月明， 任开兴. 小定额波涌沟灌技术要素的多目标模糊优化模型［J］. 农业工程学报， 2006（10）： 16-20.Gao Changzhen， Zuo Yueming， Ren Kaixing. Multi-objective fuzzy optimization model for the determination ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2006（10）： 16-20.

［15］魏家興， 费良军， 梁爽， 等. 泥沙颗粒级配组成对浑水波涌灌间歇入渗特性的影响研究［J］. 灌溉排水学报， 2023， 42（10）： 57-62， 84.Wei Jiaxing， Fei Liangjun， Liang Shuang， et al. Effects of sediment particle gradation composition on intermittent infiltration characteristics of muddy water surge irrigation ［J］. Journal of Irrigation and Drainage， 2023， 42（10）： 57-62， 84.

［16］Mahmood S， Latif M. A simple procedure for simulating surge infiltration using first-surge infiltrometer data ［J］. Irrigation and Drainage： The Journal of the International Commission on Irrigation and Drainage， 2005， 54（4）： 407-416.

［17］李岚. 浑水波涌畦灌肥液间歇入渗土壤水氮运移特性及影响因素研究［D］. 西安： 西安理工大学， 2023.

［18］龙天渝， 王延青， 安强， 等. 积水条件下连续和间歇供水对土壤入渗特性的影响［J］. 水土保持通报， 2012（3）： 7-10， 22.Long Tianyu， Wang Yanqing， An Jiang， et al. Effects of continuous and intermittent water supply on infiltration characteristic of a purple soil under ponding condition ［J］. Bulletin of Soil and Water Conservation， 2012（3）： 7-10， 22.

［19］雪静， 王全九， 毕远杰. 微咸水间歇供水土壤入渗特征［J］. 农业工程学报， 2009（5）： 14-19.Xue Jing， Wang Quanjiu， Bi Yuanjie. Soil infiltration properties with slight saline water intermittent application ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2009（5）： 14-19.

［20］严亚龙， 毕远杰， 郭向红， 等. 微咸水间歇供水方式土壤水盐分布分析［J］. 节水灌溉， 2015（6）： 39-42， 46.Yan Yalong， Bi Yuanjie， Guo Xianghong， et al. Analysis of soil water and salt distribution of saline water intermittent water supply mode ［J］.Water Saving Irrigation， 2015（6）： 39-42， 46.

［21］刘群昌， 许迪， 谢崇宝， 等. 波涌灌溉技术田间适应性分析［J］. 农业工程学报， 2002（1）： 35-40， 12.Liu Qunchang， Xu Di， Xie Chongbao， et al. Soil and water engineering adaptability of surge flow irrigation applying on farmland ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2002（1）： 35-40， 12.

［22］王文焰， 汪志榮， 费良军， 等. 波涌灌溉的灌水质量评价及计算［J］. 水利学报， 2000（3）： 53-58.Wang Wenyan， Wang Zhirong， Fei Liangjun， et al. Evaluation and calculation of irrigation quality in surge flow irrigation ［J］. Journal of Hydraulic Engineering， 2000（3）： 53-58.

［23］Ismail S M. Effect of tillage on water advance and distribution under surge and continuous furrows irrigation methods for cotton in Egypt ［J］. Irrigation and Drainage： The journal of the International Commission on Irrigation and Drainage， 2006， 55（2）： 191-199.

［24］Benham B L， Reddell D L， Marek T H. Performance of three infiltration models under surge irrigation ［J］. Irrigation Science， 2000， 20： 37-43.

［25］孙秀路， 黄修桥， 李金山， 等. 波涌灌溉土壤水氮分布的田间试验研究［J］. 灌溉排水学报， 2015（1）： 33-38.Sun Xiulu， Huang Xiuqiao， Li Jinshan， et al. Field experimental study on soil water and nitrogen distributions under surge flow irrigation ［J］. Journal of Irrigation and Drainage， 2015（1）： 33-38.

［26］Horst M G， Shamutalov S S， Goncalves J M， et al. Assessing impacts of surge-flow irrigation on water saving and productivity of cotton ［J］. Agricultural water management， 2007， 87（2）： 115-127.

［27］尹娟， 费良军， 程东娟. 循环率对波涌灌间歇入渗特性和地下水水质影响的研究［J］. 干旱地区农业研究， 2007（4）： 146-150.Yin Juan， Fei Liangjun， Cheng Dongjuan. Impact of cycle rate on intermittent infiltration characteristics and groundwater quality ［J］. Agricultural Research in the ARID Areas， 2007（4）： 146-150.

［28］任开兴. 丘陵山区波涌沟灌试验及其技术要素优化［D］. 太原： 山西农业大学， 2003.

［29］樊菊平， 费良军. 波涌灌间歇入渗减渗效果及影响因素研究［J］. 水土保持学报， 2003（6）： 62-65.Fan Juping， Fei Liangjun. Study on infiltration-reducing effect of intermittent infiltration and influential factors ［J］. Journal of Soil and Water Conservation， 2003（6）： 62-65.

［30］Mohammed M， Shafiq N， Elmansoury A， et al. Modeling of 3R （reduce， reuse and recycle） for sustainable construction waste reduction： A partial least squares structural equation modeling （PLS-SEM） ［J］. Sustainability， 2021， 13（19）： 10660.

［31］Yue C， Dang Y， Xue S， et al. A new optimal subset selection method of partial ambiguity resolution for precise point positioning ［J］. Remote Sensing， 2022， 14（19）： 4819.

［32］El-Haik B S. Manufacturing and design for six sigma （X-FSS） ［M］. University of Michigan College of Engineering Graduate Professional Programs， 2002.

［33］钟韵， 费良军， 傅渝亮， 等. 多因素影响下土壤上升毛管水运动特性HYDRUS模拟及验证［J］. 农业工程学报， 2018， 34（5）： 83-89.Zhong Yun， Fei Liangjun， Fu Yuliang， et al. HYDRUS simulation and verification of movement characteristics of upward capillary water flow in soil as affected by multi-factor ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2018， 34（5）： 83-89.

［34］费良军， 谭金兰， 韩鑫， 等. 尿素肥液间歇入渗土壤水氮运移特性试验研究［J］. 干旱地区农业研究， 2013， 31（5）： 245-250.Fei Liangjun， Tan Jinlan， Han Xin， et al. Experimental investigation on water and nitrogen transforming characteristics under intermittent infiltration of urea solution ［J］. Agricultural Research in the Arid Areas， 2013， 31（5）： 245-250.

［35］慕运动. 响应面方法及其在食品工业中的应用［J］. 郑州工程学院学报， 2001（3）： 91-94.Mu Yundong. Response surface methodology and its application in food industry ［J］. Journal of Zhengzhou Grain College， 2001（3）： 91-94.

［36］韩克光， 甄守艳， 范华， 等. 钙螯合羊骨胶原多肽的制备及表征分析［J］. 农业工程学报， 2015（21）： 301-307.Han Keguang， Zhen Shouyan， Fan Hua， et al. Preparation and characteristic analysis of calcium-chelated ossein peptide ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2015（21）： 301-307.

［37］柴朝晖， 方红卫， 姚仕明， 等. 黏性泥沙絮凝-沉降-再悬浮运动过程数学模型研究［J］. 水利学报， 2016， 47（12）： 1540-1547.Chai Chaohui， Fang Hongwei， Yao Shiming， et al. A model for the flocculation-settling-resuspension process of cohesive sediment ［J］. Journal of Hydraulic Engineering， 2016， 47（12）： 1540-1547.

［38］傅渝亮. 波涌畦灌层状土间歇入渗模型及地下水影响的肥液間歇入渗氮素运移特性［D］. 西安： 西安理工大学， 2018.

［39］Miller J J， Foroud N， Lamond B J， et al. Continuous and surge irrigation effects on hydraulic parameters and water quality ［J］. Water Quality Research Journal， 2003， 38（3）： 451-471.