Hybrid-driven Gaussian process online learning for highly maneuvering multi-target tracking*

Qiang GUO, Long TENG‡,, Tianxiang YIN, Yunfei GUO, Xinliang WU, Wenming SONG

1College of Information and Communication Engineering,Harbin Engineering University, Harbin 150001, China

2China National Aeronautical Radio Electronics Research Institute, Shanghai 200233, China

3College of Automation, Hangzhou Dianzi University, Hangzhou 310018, China

†E-mail: guoqiang@hrbeu.edu.cn; tenglong@hrbeu.edu.cn; tianxiangyin@hdu.edu.cn; gyf@hdu.edu.cn

Abstract: The performance of existing maneuvering target tracking methods for highly maneuvering targets in cluttered environments is unsatisfactory.This paper proposes a hybrid-driven approach for tracking multiple highly maneuvering targets, leveraging the advantages of both data-driven and model-based algorithms.The time-varying constant velocity model is integrated into the Gaussian process (GP) of online learning to improve the performance of GP prediction.This integration is further combined with a generalized probabilistic data association algorithm to realize multi-target tracking.Through the simulations, it has been demonstrated that the hybrid-driven approach exhibits significant performance improvements in comparison with widely used algorithms such as the interactive multi-model method and the data-driven GP motion tracker.

Key words: Target tracking; Gaussian process; Data-driven; Online learning; Model-driven; Probabilistic data association https://doi.org/10.1631/FITEE.2300348 CLC number: TN953

1 Introduction

Target tracking refers to the estimation of the motion state of the interest target, considering factors such as noisy measurements, false alarm clutter, and imperfect measurements (Da et al., 2021;Zhu et al., 2021).It is widely used in various fields,such as aircraft target tracking (Zhou et al., 2020;Zheng and Cai, 2021) and underwater target tracking(Zhang D et al.,2018).Depending on the nature of the tracked targets, target tracking algorithms can be categorized into point target tracking, extended target tracking, and group target tracking(Guo et al.,2019,2020a;Wang et al.,2021).The primary focus of this paper is to address the challenge of maneuvering posed by point target tracking.It uses kinematic information to estimate the target’s state,which includes parameters such as position,velocity,and acceleration(Li et al.,2019b;Li and Hlawatsch,2021).

The central concept of maneuvering target tracking focuses on enhancing the degree of correspondence between the tracking model and the real motion model of the target(Li et al.,2019a).Maneuvering target tracking algorithms are classified into two categories,which are the model-driven and datadriven approaches.Model-driven algorithms rely on the prior motion models of the target.The statespace model is modeled as a Markov process by using prior model information,thereby describing the relationship between the target state vectors at adjacent time slots(Guo et al.,2015;Li et al.,2017).Typical model-driven methods include the interactive multimodel (IMM) method (Wu et al., 2021), where the tracking results of different models are appropriately weighted,and the variable structure IMM(VSIMM),the core of which is the model set selection algorithm.In terms of computational complexity and performance, IMM has been demonstrated as the most cost-efficient approach.

Nevertheless,as the maneuverability of the target continues to advance and maneuvering patterns become more complex, the target trajectory may consist of many models, and the associated maneuvering parameters such as acceleration and angular velocity tend to be larger.Model-driven methods face several application limitations: (1) Poor tracking ability and environmental adaptability.If the target’s maneuvering patterns lie beyond the scope of the prior model set,it can result in model mismatch,leading to decrease in the tracking performance of the model-driven algorithm or even causing the filter to diverge.(2) State estimation delay.Because the target motion model is unknown, as well as owing to model switching, model-driven methods need to gather sufficient measurements to precisely estimate the target state.(3)High computational complexity.In the case of highly maneuvering targets,the uncertainty in their maneuvers is significant, and their trajectories may encompass an infinite number of motion models.For model-driven approaches,it becomes impractical to construct an excessively large model set to account for all possible maneuvers.

In response to the constraints of the modeldriven approaches, researchers have incorporated neural networks, which possess robust learning capabilities, into the maneuvering target tracking methodology.Zhang XR et al.(2019) and Deng et al.(2020) used long short-term memory (LSTM)neural networks to discern target maneuver parameters, such as the maneuver model, acceleration,and angular velocity.Liu JX et al.(2020)employed neural networks to directly predict the position estimation error of the target, enhancing the overall state estimate.Tian et al.(2022) proposed the multimodel Gaussian mixture probability hypothesis density (MM-GM-PHD) filter based on LSTM.Moreover, in Xiong et al.(2022), an end-to-end method was used to estimate the target state.The central concept is to learn the essential steps of the Bayesian filter, including the state transition matrix, process noise covariance matrix, and measurement noise covariance matrix.Nonetheless, in implementing the aforementioned neural network based maneuvering target tracking methods, we are still faced with certain obstacles,and these are(1)poor interpretability and (2) the fact that for small sample learning, significant challenges continue to be encountered.

In addition to neural networks,data-driven maneuvering target tracking methods encompass Gaussian process (GP), which consists of a series of random variables that follow a Gaussian distribution and fits data to an unknown function using different distributions obtained(Rasmussen and Williams,2006).Huber (2014) proposed a method based on recursive GPs, enabling the online learning of GP hyperparameters with low computational burden.Aftab and Mihaylova (2021) presented a Gaussian process motion tracker (GPMT) algorithm.This algorithm has the capability to learn an arbitrary motion model online during each tracking period.Subsequently, the target state is estimated using the learned model and measurements.GPMT can flexibly switch between numerous or even unlimited motion models.A maneuvering target tracking method based on GPPF was proposed in Sun et al.(2020), wherein the researchers integrated the particle filter (PF) into GP target tracking.GP was extended to distributed multiple sensors in Liu XC et al.(2022).Guo et al.(2022) proposed a novel approach by combining IMM and GP for track segment association of maneuvering targets, and this approach demonstrated a superior performance in comparison with both the model-driven and datadriven methods.The essence of GP lies in learning unknown models through the covariance kernel function.Therefore, Aftab and Mihaylova (2020) conducted an analysis on the influence of different kernels and training data on the performance of target tracking.Furthermore, GP has found applications in maneuvering ship tracking(Guo et al., 2020b).

However, in the context of a more intricate maneuvering target within a cluttered background,where the target encompasses an infinite spectrum of motion models and its maneuvering parameters are more extensive and exhibit rapid fluctuations, GPMT might, due to the influence of clutter,encounter substantial state prediction errors,potentially leading to target loss.In this paper we present a novel online learning approach for enhancing the tracking precision of intricate maneuvering targets amidst cluttered environments.The method uses a hybrid-driven GP as the fundamental framework.Building upon this foundation and in conjunction with the generalized probabilistic data association(GPDA) algorithm, robust tracking of highly maneuvering multiple targets is achieved.

2 Background

The standard GPs are presented in this section.The core of a GP that can learn any unknown function is comprised of the mean and covariance(kernel)functions.In most applications, the mean remains constant or zero (Huber, 2014).Thus, the design of the covariance emerges as a crucial aspect within GP.Readers can refer to Huber (2014) for further information regarding various mean and covariance functions.The functionf(·)of interest,which is unknown and subject to additive noise, is represented as follows:

wherexrepresents the measurement vector,tis the input vector,andτrefers to the Gaussian white noise characterized by a mean of zero and a variance ofσ2n.Considering the prior data (ti,xi),tirepresents the input andxirepresents the corresponding output,i=1,2,···,n.f(·)can be modeled with GP as

whereIrepresents the identity matrix, andk(t,t*)is the kernel function between the input vector of test data and the input vector of training data, which is expressed as

Here,the number of test data samples is denoted byl, andk(tn,t*l) is the kernel function between thenthinput of training data and thelthinput of test data.tandt*represent the input vectors forfandf*, respectively.Similarly, we can obtaink(t,t),k(t*,t), andk(t*,t*).According to Eq.(3), the prediction distribution (Huber, 2014) of the test is obtained as

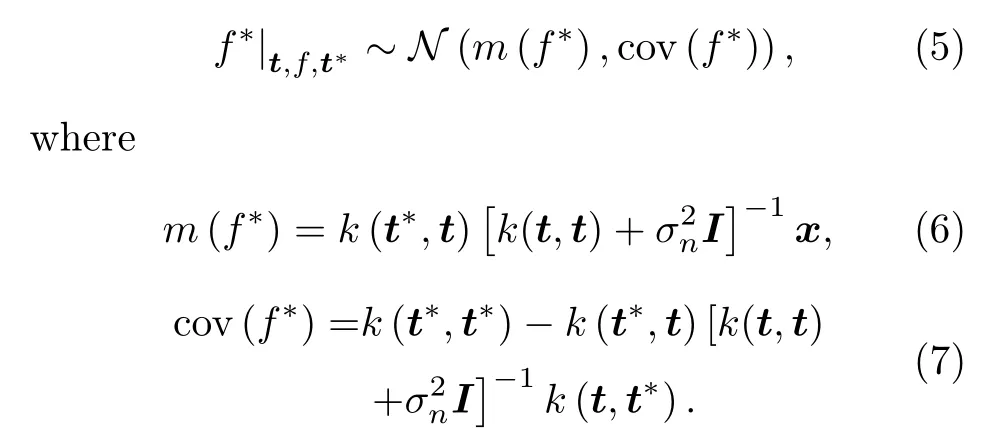
Here,m(f*) and cov(f*) represent the predicted mean and covariance,respectively.

3 Hybrid-driven highly maneuvering multi-target tracking

In this section we provide a comprehensive explanation of the proposed approach.The fundamental idea is to integrate the time-varying constant velocity (CV) model into GPMT, thereby enhancing predictive abilities to effectively track extremely maneuverable targets amidst cluttered surroundings.Expanding on this foundation, the methodology integrates GPDA to enable simultaneous tracking of multiple highly maneuvering targets.The method proposed here uses a limited set of previous measurements for target state estimation and operates under the assumption of orthogonal coordinate axes.

First, GP is employed to model the nonlinear function of thexcoordinate,and the procedure is repeated for theycoordinate.For more specifics,readers can refer to Section 3.1.Next, the training set is formed by choosing the precedingd-dimensional measurement.The hyperparameters are learned through a maximum likelihood estimator based on the training set, as explained in Section 3.2.Once again, the time-varying CV model is employed for state prediction, as indicated in Section 3.3.Subsequently, the GPDA algorithm is employed to accomplish the correlation matching between measurements and targets, as explained in Section 3.4 in greater detail.Ultimately, GP is applied for both state and training set updates; further elaboration can be found in Section 3.5.The state update process resembles the state update in the Kalman filter,wherein the target’s state estimate is determined by using both the measurement and the state prediction.The training set update entails using GP to optimize the distribution of the prior training set,thus preventing underfitting.

3.1 GP modeling

According to Eqs.(1)and(2),the unknown nonlinear functionfand the corresponding observation function (Huber, 2014)can be defined as

During the target tracking process,once the interconnection between adjacent data samples is comprehended,target state estimation can be performed based on this interrelation.The kernel function in GP can capture the relationship between different input points.Hence,the kernel function is employed to comprehend the link among the training data,enabling the modeling of the target’s motion pattern.This learning process is conducted at each time step,allowing it to acquire any unknown function from the training data in real time.In the context of target tracking, the unknown function encompasses all potential maneuvering modes of the target.

3.2 Hyperparameter optimization

3.3 Prediction

During the prediction process,we use the timevarying CV model instead of GP forecasting.The time-varying CV model involves the estimate of the velocity based on the last two variables (xt-1andxt-2) of the training setXtbefore a prediction is made.The velocity estimateVxt－1for thexcoordinate can be expressed as

3.4 Generalized probabilistic data association algorithm

In this subsection, we perform correlation matching between the measurement and the target at timetbased on the prediction vector ˜St.The proposed method introduces the concept of deterministic association measurement of the GPDA algorithm(Pan et al., 2005;Guo et al., 2016).Under this concept, the belief is that both the measurement and target can be reused, and that a generalized joint event is constructed.The association probability is obtained according to the Bayesian rule, to determine the association measurement.

First, a tracking gate is created with the predicted vector ˜Stas its center, and the permissible measurements are determined based on this gate.This can be formulated as

whereZt(i) represents theithmeasurement at timet,Rdenotes the measurement noise covariance,Btdenotes the residual covariance,Nrepresents the number of measurements,Hdenotes the observation matrix, andγis the hypothesis testing threshold ofχ2.If inequality(15)holds true,it indicates that the measurements within the gate collectively contribute to the target.

Then, the association probability matrixGis computed based on the predicted state ˜St, the predicted covariance ˜Pt,the residual covarianceBt,and the associated valid measurements(Pan et al.,2005):

wheregijis the probability density between measurementiand targetj,i= 0,1,...,m,j= 0,1,...,J,andmandJare the numbers of measurements and targets respectively.The calculation ofGis divided into three parts: (1) The first row,g0j=(nV)-1(1-PDPG), represents the probability density between measurement 0 and targetj(j/= 0),wherePDis the detection probability,PGis the gate probability,Vis the volume of the gate, andnis the coefficient.(2) The first column,gi0=λ, represents the probability density between target 0 and measurementi(i/= 0), whereλis the clutter density,target 0 means no target of interest,which may be a new target or a false target, and measurement 0 means no measurement (that is, the target is not detected).(3)The probability density between measurementiand targetj(i/=0,j/=0)is

Finally, the correlation probabilityβijof measurementiand targetjis calculated based on the normalizedεijandξij,to obtain the associated measurementof targetj, where

Here,cis the normalization coefficient,ρis the weight factor,his the target index, andris the measurement index.

3.5 Update

This subsection consists of two parts: the target state update and the training set update.The state update is similar to the Kalman filter update, and the state and covariance of thexcoordinate are updated based on thex-componentxtof the associated measurementZt.The update equations are

where ˜Ktis the gain matrix.

The method proposed above, which combines elements of both the model-driven and data-driven approaches, is called the hybrid-driven GPMT and is summarized in Algorithm 1.

Algorithm 1 Hybrid-driven GPMT Input: Xt, Tt, θ Output: ˆμft, ˆCft , μft, Cft , Ct 1: Hyperparameter θ is learned via Eq.(11)2: Compute the predicted state ˜St via Eq.(13) and the predicted covariance ˜Pt via Eq.(14)3: Compute the associated measurement Zt according to inequality (15) and Eqs.(16)–(20)4: Compute mean ˆμft and covariance ˆCft of the estimated state via Eqs.(21) and (22), respectively 5: Compute cross-covariance Ct via Eq.(23)6: Compute mean μf t and covariance Cft of the training set by Eqs.(26) and (27), respectively

4 Performance validation

In this section, the advantages of the proposed method have been verified under the prevalence of challenging scenarios.Section 4.1 provides an introduction to these scenarios and the configuration of parameters.The comparison methods and their parameter settings are given in Section 4.2, while the simulation results are discussed in Section 4.3.

4.1 Testing scenarios and parameter settings

In a two-dimensional space, the target surveillance region has a size ofV= πr2, withr= 50 km,and the motion state of the target denoted asX=[x,y,Vx,Vy]Tincludes the position and velocity components.There are four targets with randomly initialized positions.The maximum acceleration for target maneuvering is 8×9.8 m/s2.The range of the angular velocityωof the maneuver is [-18°,18°].The acceleration and angular velocity for each target maneuver are randomly set.The duration of each maneuver is randomly determined within [8,10] s.The target velocity is within [100,680] m/s.The initial target velocity is randomly assigned within[100,300]m/s.The detection probability is given asPD= 0.98.Clutter returns can be generated using a Poisson process withK(z) =λV c(z), where the clutter density isλ= 0.5× 10-7m-2.The clutter is assumed to have a uniform spatial distribution throughout the surveillance region,as represented byc(z).Given the unknown target motion model, the state equation can be formulated as

The state equation consists of different models represented by the first to the fourth rows, corresponding to the CV,constant acceleration(CA),coordinated turn (CT), and nonlinear models, respectively.a=[ax,ay]Tis the acceleration vector,whereaxandayrepresent the acceleration components of thex- andy-coordinate axes respectively.ωis the angular velocity.F1,F2, andF3are expressed in terms of

The state transition function of the nonlinear model is denoted byf.Xt-1andXtrepresent the target states.The control matrixDand process noise matrixUare given by

Here,ξx=ξy=300 m.

The simulation time is 100 s.The sampling periodTdata= 1 s.The performance of the tracking method is evaluated through 500 Monte Carlo simulations.The root mean square error(RMSE) is

whereNMCis the number of Monte Carlo simulations, andqikand ˆqikare the true and estimated values,respectively.

4.2 Compared methods

For IMM, as there is no prior knowledge about the target motion,a standard combination of models(CV, CA, and CT) is chosen,which encompasses 31 models(1 CV model,24 CA models,and 6 CT models).For the CV and CA models, the acceleration vectorasatisfies

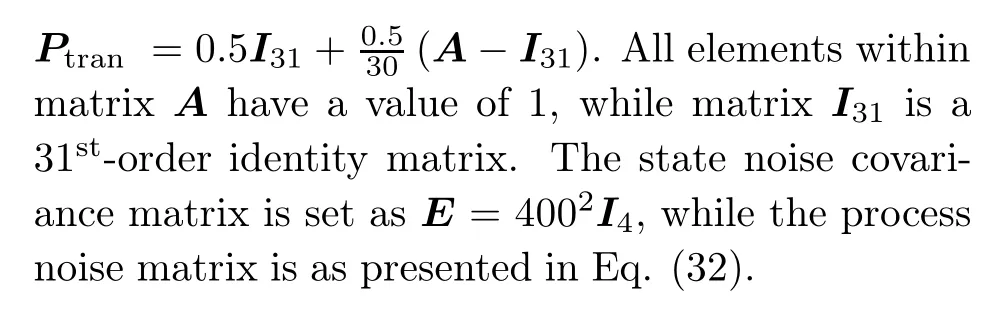
4.3 Results

Fig.1 presents the tracking results obtained from the proposed method, demonstrating its ability to achieve satisfactory tracking performance for highly maneuvering targets in cluttered environments.RMSE values of the proposed method,GPMT, and IMM are depicted in Fig.2.The mean RMSE is shown in Table 1.It can be seen that the proposed method exhibits a clear advantage in position estimation compared to the GPMT and IMM methods.Both IMM and GPMT have a poor tracking performance.The reason is that the monitored targets are being highly maneuverable in a cluttered environment.Their maneuvering attributes encompass wider parameter ranges and display rapid changes.The tracking effectiveness of IMM is constrained by the collection of predefined models.The precision of tracking diminishes when the predefined model set fails to encompass the complete motion pattern of the target.IMM is unable to encompass all the maneuvering modes of highly maneuvering targets using a predefined set of models.

Furthermore, another crucial factor contributing to reduced tracking accuracy of IMM and GPMT is the presence of background clutter.Due to clutter,prediction errors are magnified, subsequently affecting data association and the state update process.With the passage of time, errors will progressively accumulate.To sum up, the poor tracking performance of both IMM and GPMT can be primarily attributed to the presence of clutter and the inherent constraints of the algorithms.The proposed method integrates the time-varying CV model into GPMT to improve the prediction error and attain satisfactory tracking performance.

However, there is no significant difference between the three methods in velocity estimation, and this is attributable to the fact that velocity measurement is derived from the difference in position measurements.However,for highly maneuvering targets,this method of obtaining velocity measurements may not yield accurate results.Notably, the proposed method estimates the elements in the state vector(x,y,Vx,Vy)independently.

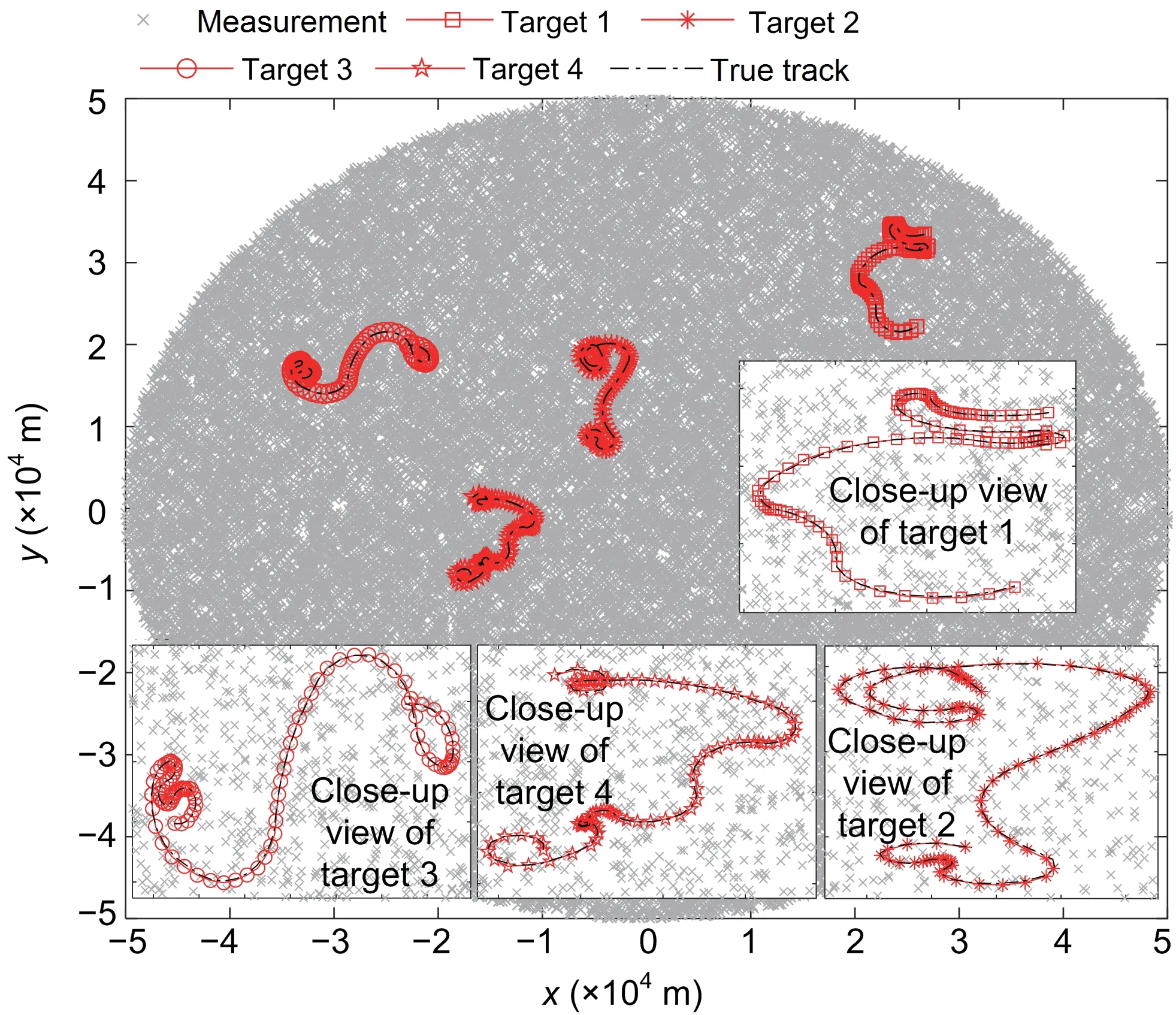
Fig.1 True target tracks and position estimates

Table 1 Mean root mean square error

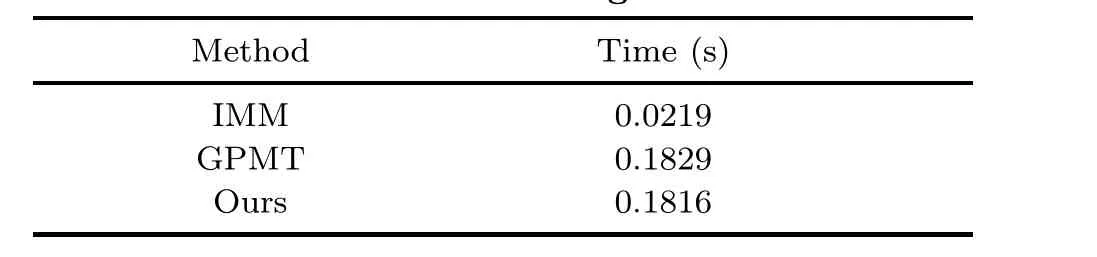
Table 2 Processing time

The code is executed on a Windows 10 computer with an i7-9750H 2.6 GHz CPU.The Matlab version is 2020b.Table 2 displays the processing time involved in the execution of each iteration under each of the methods, that is, IMM, GPMT, and the proposed method,for a total of 500 Monte Carlo simulations.The processing time of the proposed method falls between those of the IMM and GPMT methods.

5 Conclusions

This paper presents a novel approach for highly maneuvering multi-target tracking, combining the strengths of data-driven GP learning and the stability of the time-varying CV model prediction.The proposed hybrid-driven method outperforms existing techniques such as IMM and GPMT under challenging scenarios involving highly maneuvering targets in cluttered environments.

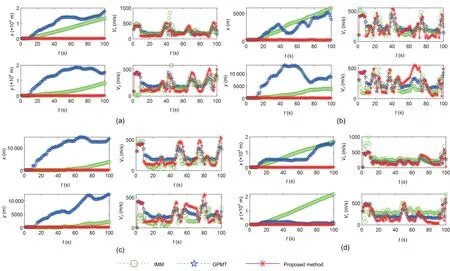
Fig.2 Root mean square error of the estimated states for targets 1 (a), 2 (b), 3 (c), and 4 (d)

Contributors

Qiang GUO and Long TENG designed the research and addressed the problems.Long TENG processed the data and drafted the paper.Yunfei GUO and Tianxiang YIN helped with the technical information.Xinliang WU and Wenming SONG helped organize the paper and supervised the study.Long TENG revised and finalized the paper.

Compliance with ethics guidelines

Qiang GUO,Long TENG,Tianxiang YIN,Yunfei GUO,Xinliang WU, and Wenming SONG declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.