Magnetically driven microrobots moving in a flow:a review*#

Jiamiao MIAO,Xiaopu WANG, Yan ZHOU, Min YE,Hongyu ZHAO, Ruoyu XU, Huihuan QIAN

1School of Science and Engineering, the Chinese University of Hong Kong (Shenzhen), Shenzhen 518172, China

2Shenzhen Institute of Artificial Intelligence and Robotics for Society (AIRS), Shenzhen 518129, China

†E-mail: wangxiaopu@cuhk.edu.cn; hhqian@cuhk.edu.cn

Abstract: Magnetically driven microrobots hold great potential to perform specific tasks more locally and less invasively in the human body.To reach the lesion area in vivo, microrobots should usually be navigated in flowing blood, which is much more complex than static liquid.Therefore, it is more challenging to design a corresponding precise control scheme.A considerable amount of work has been done regarding control of magnetic microrobots in a flow and the corresponding theories.In this paper, we review and summarize the state-of-the-art research progress concerning magnetic microrobots in blood flow, including the establishment of flow systems, dynamics modeling of motion, and control methods.In addition, current challenges and limitations are discussed.We hope this work can shed light on the efficient control of microrobots in complex flow environments and accelerate the study of microrobots for clinical use.

Key words: Microrobot; Flow; Dynamics modeling; Control https://doi.org/10.1631/FITEE.2300054 CLC number: TP242

1 Introduction

Microrobots refer to robots with a size up to a few millimeters (Nelson et al., 2010).So far, they have been widely used in drug delivery (Sitti et al.,2015; Erkoc et al., 2019; Zhang HY et al., 2021),tissue engineering (Li JY et al., 2018; Gyak et al.,2019; Yan et al., 2020), minimally invasive surgery(Bailly et al., 2011; Ullrich et al., 2013; Sitti et al.,2015), embolization (Go et al., 2022; Law et al.,2022),and micro-assembly tasks(Adam et al.,2019).Because of their tiny size, microrobots can access and be navigated in confined and hard-to-reach sites in vivo (Ceylan et al., 2019).With the extraordinary progress of microrobots regarding autonomous actuation, medical imaging, navigation, and functionalization, it becomes more promising for microrobots to be used clinically (Li ZY et al., 2021).For actuation of microrobots, various types of energy could be used, including light (Hu WQ et al.,2011;Palagi et al.,2019;Li DF et al.,2020;Sitti and Wiersma, 2020), magnetic fields (Peyer et al., 2013;Khalil et al., 2014b; Li JY et al., 2018), ultrasound(Ishihara and Furukawa,1991;Feng et al.,2016;Lee et al., 2020), chemical energy (Martel, 2012; Park et al., 2013; Chen et al., 2014), electricity (Pawashe et al., 2009; Kim and Kim, 2015; Moo et al., 2017),and combinations of them (Khalil et al., 2014a; Li DH et al., 2015;Ahmed et al., 2021).

As for clinical uses,microrobots should be operated in complex flowing blood environments.Thus,a clear understanding of how microrobots behave in a flow is essential.So far, there have been a significant number of works regarding the motion of microrobots in the flow.In the beginning, most of these studies were conducted in laboratory environments (Choi J et al., 2010a; Mathieu and Martel,2010; Ahmed et al., 2021).The study of practical applications in vivo has just become popular recently(Servant et al.,2015;Ceylan et al.,2017,2019;Zhang HY et al., 2021; Go et al., 2022; Law et al., 2022).For studies in laboratory environments, flow types are considered important factors that affect the microrobot motion control.Regarding in vivo studies,the vascular environment is even more complicated,as both the vascular morphology and the blood flow conditions are variable (Manamanchaiyaporn et al.,2020).Blood capillaries can have a diameter of as small as 8 μm, while the flow rate inside is usually＜1 mm/s.However, aortas can have a diameter of about 25 mm and a flow rate of about 245–630 cm/s(Doutel et al., 2021).Flow disturbance and blood viscosity also contribute to the complexity of the vascular environment (Demircali et al., 2021a, 2021b).To achieve clinical use of microrobots, it is essential to understand how all the flow-related parameters mentioned above influence the motion control of microrobots.

Specifically, studies on microrobot motion in a flow so far have been conducted mainly regarding magnetically driven microrobots (Martel et al.,2007; Mathieu and Martel, 2010; Wang QQ et al.,2021).Magnetic irradiation, which provides the actuation of these microrobots, is harmless to the human body and can penetrate deep tissues (Sitti and Wiersma, 2020).In addition, magnetically actuated microrobots are relatively easy to obtain through various micro-/nanofabrication technologies (Jang et al., 2019; Sitti and Wiersma, 2020; Ebrahimi et al., 2021).Therefore, this review focuses on the motion control of magnetically driven microrobots in a flow.To simplify, in this paper, microrobots are magnetically driven unless otherwise specified.

In this review, motion and control studies regarding magnetically driven microrobots are summarized from three aspects,i.e.,flow system design and construction,dynamics modeling of motion,and control strategies and methods.The challenges of current research are also discussed regarding each part.The establishment of the flow system involves mainly building flow systems with different flow types,which is crucial for understanding the motion of microrobots.Dynamics modeling includes the theoretical analysis of the relationship between the motion of microrobots and the forces or torque exerted on them.Various factors that influence motion are also introduced.Microrobot control strategies in a flow refer to open-loop control and closed-loop control(including proportional-integral-derivative (PID) control, model predictive control (MPC), backstepping control, and extended state observer (ESO) based model-free control).Some typical examples with specific control methods are also introduced.Finally,potential applications are summarized.This review reflects on the current progress and challenges of microrobot motion in a flow.Hopefully, it will provide meaningful guidance for future clinical use of microrobots.

2 Flow systems

To study microrobot motion in various flows,it is essential to establish flow systems, which may consist of flow generators, flow channels, injection devices, sensors, actuation equipment, and imaging equipment.Based on their similarity level with actual blood systems,flow systems that have been used in the study of microrobot motion can be categorized into four types: laboratory flow systems(Martel et al., 2007;Choi J et al., 2010a,2010b;Mathieu and Martel, 2010; Arcese et al., 2012; Li JY et al.,2018;Alapan et al.,2020;Ahmed et al.,2021;Zhang HY et al., 2021), artificial blood systems (Alapan et al., 2020; Xu HF et al., 2020), ex vivo systems(Wang QQ et al.,2021),and in vivo systems(Martel et al.,2007;Choi J et al.,2010b;Servant et al.,2015;Li JY et al.,2018;Li DF et al.,2020;Zhang HY et al.,2021).The similarity levels of these systems with actual blood systems are determined mainly by the material properties of their channels.For each system, the properties of the flow are highly dependent on the properties of the fluid materials flowing in the channel, such as density and shear stress.In this section, the main flow types and flow systems that have been used for the study of microrobot motion are summarized and discussed.Detailed parameters of some typical flow system examples are listed in Table S1 in the supplementary materials.

2.1 Flow types

So far, most flows used in the study of microrobot motion are in cylindrical channels (Martel et al., 2007; Choi J et al., 2010a, 2010b; Li JY et al., 2018; Alapan et al., 2020; Zhang HY et al.,2021), while rectangular tubes were also used in a few works(Sanchez et al.,2011;Khalil et al.,2014a,2016;Alapan et al.,2020;Xu HF et al.,2020;Demircali et al., 2021a, 2021b).Compared with cylindrical channels,rectangular tubes with customized sizes are relatively easier to obtain in the lab.However,flow systems with rectangular tubes have low similarity with blood vessel flow because of the existence of corners.Therefore,rectangular tubes were only used in a few laboratory flow systems, while cylindrical channels were used not only in laboratory systems but also in artificial blood systems and ex vivo/in vivo blood systems.The flow types used in these systems include mainly Poiseuille flow and pulsatile flow.

2.1.1 Poiseuille flow

Poiseuille flow refers to pressure-induced flow in a long pipe, and it has a spatial parabolic feature(Fig.1a),which means that the flow rate is the highest in the middle of the channel and the lowest at the channel wall (Ahmed et al., 2021).With the Reynolds numberResmaller than 2300, the flow is laminar, so the Hagen-Poiseuille law is applicable.In this case, Poiseuille flow can be used as a deeply simplified vascular flow model (Pfitzner, 1976).So far, Poiseuille flow has been used in many flow systems to study microrobot motion, including laboratory flow systems (Mathieu and Martel, 2006, 2010;Acemoglu and Yesilyurt, 2015;Ahmed et al., 2021),artificial blood systems (Alapan et al., 2020)and ex vivo blood flow systems(Wang QQ et al., 2021).

2.1.2 Pulsatile flow

Pulsatile flow means a flow with periodic variations (Reis and Hanriot, 2017).Fig.1b shows a typical example of pulsatile flow.Like Poiseuille flow,pulsatile flow in a cylindrical channel also has a spatial parabolic profile (Sadelli et al., 2017; Daems et al., 2020).The pulsatility of pulsatile flow makes it more similar to vascular flow, compared with Poiseuille flow.So far, pulsatile flow has also been used in many flow systems to study microrobot motion,including laboratory flow systems(Tamaz et al.,2008;Choi J et al.,2010a,2010b;Ahmed et al.,2021;Wang QQ et al., 2021) and in vivo blood flow systems(Martel et al.,2007;Choi J et al.,2010a,2010b;Servant et al.,2015;Li JY et al.,2018;Doutel et al.,2021;Zhang HY et al.,2021).

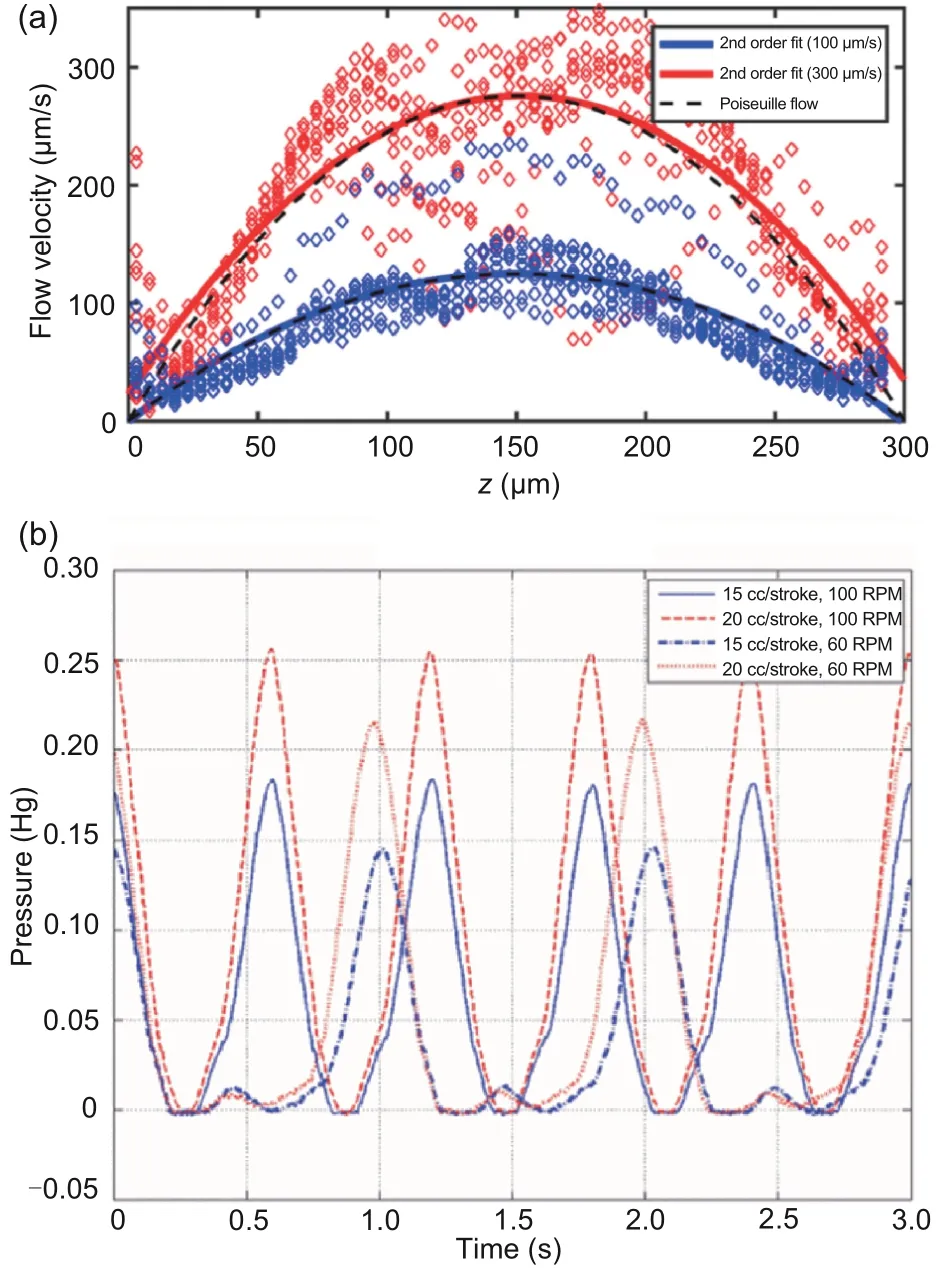
Fig.1 Spatial parabolic profile of Poiseuille flow (a)and pulsatile waveform of pulsatile flow (b).(a) is reprinted from Ahmed et al.(2021), Copyright 2021,with permission from Springer Nature, and (b) is reprinted from Choi J et al.(2010a), Copyright 2010,with permission from IEEE

2.2 Laboratory flow systems

Laboratory flow systems refer to systems that are based on artificial channels and liquid solutions.Such systems generally consist of artificial channels that are filled with liquids, pumps to generate the flow, sensors to measure the flow rate, and devices to obtain the position of microrobots (camera, pressure transducer, etc.) (Mathieu and Martel, 2006; Tamaz et al., 2008; Choi J et al., 2010a,2010b;Acemoglu and Yesilyurt,2015;Ahmed et al.,2021; Yang SH et al., 2022).The artificial channels of laboratory flow systems are usually made of glass (Ahmed et al., 2021) or polydimethylsiloxane(PDMS)(Ahmed et al.,2021;Zhang HY et al.,2021).In Zhang HY et al.(2021), the velocity of microrobots on PDMS was higher than that in the vessel,suggesting that the roughness of the channel influences the propulsion under magnetic field.In addition, liquid flowing inside the channel of laboratory flow systems is usually water (Choi J et al., 2010a,2010b; Mathieu and Martel, 2010; Servant et al.,2015;Ahmed et al.,2021;Demircali et al.,2021b)or mixtures of glycerol and water in different concentrations(Tamaz et al.,2008;Demircali et al.,2021a;Wang QQ et al., 2021, 2022; Yang SH et al., 2022).As the properties of these materials are easy to formulate, laboratory flow systems are ideal simplified models for initial studies, although they are nominally similar to actual blood systems.

Regarding motion studies in laboratory systems based on Poiseuille flow,the channel design is usually emphasized regarding how the microrobots are transferred into the flow and how the experiment is carried out(Mathieu and Martel,2006;Acemoglu and Yesilyurt, 2015; Özahi and Çarpınlıoğlu, 2015; Ahmed et al., 2021).For each study, decisions regarding these issues are made according to the experimental purposes.For example, in Ahmed et al.(2021),several tube sizes were chosen to mimic physiological flow conditions.Within a rotating magnetic field,a microswarm (a swarm of microrobots) was generated and actuated to move upstream.By applying and adjusting the external acoustic field, the behavior of the microswarm within a flow was studied.The detailed experiments and results are discussed in Section 3.1.5.

In motion studies in laboratory systems based on pulsatile flow,a pulsating pump is needed.In the works of Choi and coworkers,a pulsating pump was used to generate pulsatile flows with different waveforms(systole,diastole,or sinusoidal),which can be measured by a pressure transducer (Choi J et al.,2010a).In addition,when measuring waveforms,the pressure transducers were used as the feedforward input of the controller,enabling precise stabilization(Choi J et al., 2010a)and locomotion(Choi J et al.,2010b)of microrobots.

The laboratory flow systems are irreplaceable for the basic study of microrobot motion in a flow because the channels used in these systems are cheap and reusable.However, these channels are significantly different from blood vessels,and the flows generated inside cannot represent natural blood.Therefore, to achieve more advanced motion studies, flow systems that can better mimic blood vessel flow are needed.

2.3 Artificial blood systems

Compared with laboratory flow systems, the fluid material (medium) used in artificial blood systems is real blood, instead of water or glycerol, increasing the similarity of artificial blood systems with actual blood systems.To avoid blood coagulation, heparin-loaded liposomes were used to functionalize the microrobots (Xu HF et al., 2020).In Xu HF et al.(2020), a soft microfluidic chip was fabricated using PDMS to form the channel of the artificial flow system, as shown in Fig.2a.In addition,a continuous or pulsatile blood flow was generated by controlling the flow waveform with a syringe pump.In Alapan et al.(2020),artificial flow systems with two-dimensional (2D) and three-dimensional(3D) blood channels were developed, using mouse CD1 whole blood as the flow medium (Figs.2b and 2c).Endothelialized microfluidic systems were used for experiments to mimic real blood vessels (Alapan et al., 2020).A series of flow rates were used in their work to mimic the motion of microrobots in real blood flow environments with different shear stress.Within these artificial flow systems, the capabilities of microrobots to move upstream or on inclined surfaces were tested.

2.4 Ex vivo systems

To move a step closer to the actual blood system of humans,organs of dead animals were used as ex vivo blood systems for the study of microrobot motion in Wang QQ et al.(2021).The fluid materials used here were blood.As shown in Fig.3, a porcine coronary artery was used for the ex vivo experiment,and a Doppler ultrasound system was used for real-time tracking.A programmable pump was used to generate the pulsatile flow in this system.Microrobot suspension in phosphate-buffered saline(PBS)buffer was injected into the artery with a percutaneous transluminal angioplasty (PTA) balloon dilation catheter.Because the flow rate was high, a balloon was inflated first to tune the flow avoiding losing microrobots before the injection.After the swarm formation of the microrobots was observed with dynamic Doppler signals, the balloon was deflated to restore normal blood flow.

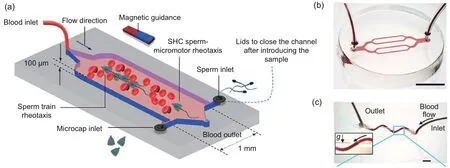
Fig.2 An artificial blood system for sperm micromotors (a), an endothelialized microfluidic system with branched channels (scale bar, 5 mm) (b), and a 3D microfluidic system (c).(a) is reprinted from Xu HF et al.(2020), Copyright 2020, with permission from ACS Publications; (b) and (c) are reprinted from Alapan et al.(2020), Copyright 2020, with permission from AAAS

Fig.3 Setup of ex vivo experiments (a) and details of the plastic box in the photo on the left (b).Red arrows show the steering of the transducer.Reprinted from Wang QQ et al.(2021), Copyright 2021, with permission from AAAS

2.5 In vivo systems

Moreover, the motion of microrobots has been demonstrated in living animals, including micropigs or swine (Martel et al., 2007; Choi J et al., 2010a),mice (Servant et al., 2015;Li JY et al., 2018; Li DF et al., 2020; Zhang HY et al., 2021), and zebrafish embryos (Li JY et al., 2018; Jia et al., 2022).As actual blood systems,in vivo systems are more complex than other systems, but they can truly reflect the actual clinical situation.For these in vivo experiments, it is essential to have an effective actuation device for microrobot navigation and an in vivo imaging system for motion control and tracking of microrobots.

The imaging methods used for these in vivo experiments include bi-plane X-ray fluoroscopy (Choi J et al.,2010a),X-ray angiography(not very precise)(Martel et al., 2007),and fluorescence imaging(Servant et al.,2015;Li JY et al.,2018;Zhang HY et al.,2021).Li JY et al.(2018) performed in vivo transportation and automatic navigation of mesenchymal stem cell-cultured microrobots to a target site in the yolks of a zebrafish embryo under the control of a magnetic gradient field and tracking with a microscope.The HeLa cell delivery ability of microrobots was tested in nude mice, while X-ray was used for imaging.Servant et al.(2015)navigated a swarm of functionalized helical microrobots with a titanium oxide layer in the peritoneal cavity of a mouse with the control of a magnetic field,while whole-body fluorescence imaging was used for tracking.

3 Dynamics modeling of the motion of microrobots in a flow

3.1 Theoretical analysis

For the simplified model of magnetically driven microrobots moving in a flow, magnetic forcesFmand magnetic torquesτmexerted on them provide the actuation(Martel et al.,2007;Tamaz et al.,2008;Choi J et al.,2010a,2010b;Arcese et al.,2012;Khalil et al., 2014a; Alapan et al., 2020; Wang B et al.,2021).At the same time, forces and torques caused by the surrounding environment provide resistance(Sanchez et al., 2011; Arcese et al., 2012; Acemoglu and Yesilyurt,2015;Khalil et al.,2016;Sadelli et al.,2017; Ahmed et al., 2021; Demircali et al., 2021a,2021b;Wang QQ et al.,2021).Moreover,microrobot motion can be regulated by factors that do not provide actuation or resistance directly.For example,an acoustic field can be applied to regulate microrobot motion by adjusting their position in the flow(Ahmed et al., 2021).Regarding spherical or cylindrical microrobots surrounded by the flow,forces exerted on them would affect their movements, while torques exerted on them would cause only spinning of the microrobots without any net displacement.Regarding helical microrobots surrounded by the flow,in addition to forces,torques exerted on them can be transferred into their forward movements, because the spinning of helical microrobots caused by torques is non-reciprocal motion (Peyer et al., 2013).The conclusion is supported by the scallop theorem proposed by Purcell(1977).Microrobots motion in flow is at a low Reynold number (Re ≪1), under which circumstance the Navier-Stokes equations are simplified to be time-independent(as shown in Eq.(1)).In this case, objects with reciprocal motion, changing the body into a certain shape and then going back to the original shape by going through the sequence in reverse, cannot go anywhere, while objects with non-reciprocal motion do.Because the corkscrew motion of a helix is a typical non-reciprocal motion,helical microrobots could move forward with torque exerted on them (Purcell, 1977; Lauga and Powers,2009; Servant et al., 2015).Furthermore, the detailed geometry parameters of helical microrobots would influence their motion efficiency (Wang XP et al., 2022).

Provided by a magnetic field with the magnetic flux density ofB, magnetic forcesFmand magnetic torquesτmexerted on a microrobot with the magnetic volume ofVmand the magnetization ofMcan be calculated with Eqs.(2)and(3):

In addition to magnetic forces (and torques)for actuation,there are forces(and torques)exerted on microrobots caused by the complex flow environment and other external stimulations.Because there are plenty of flow-related parameters,the calculation of these forces (and torques) is much more complicated than that of magnetic forces (and torques).For a clear and easy understanding, forces that affect the motion of all kinds of microrobots are discussed first in this section.Then, torques are discussed specifically for the helical microrobot cases and microswarms.

Based on Newton’s law, the main governing forces that affect the motion of microrobots in the flow can be summarized as (Arcese et al., 2012;Khalil et al., 2016; Sadelli et al., 2017; Meng et al.,2020; Ahmed et al., 2021; Demircali et al., 2021a,2021b)

Here,mandvare the mass and the translational velocity of the microrobot, respectively.Fmrepresents the magnetic propulsion force.Fdrepresents the hydrodynamic drag force.FQrepresents the force caused by the time-derivative of the flow rate.Warepresents the apparent weight of the microrobots, which means the sum of gravity and buoyant force.Fcrepresents the contact force.Fvdwrepresents the van der Waals force.Felrepresents the electrostatic interaction force between the microrobot and the vessel walls.Fotherrepresents the forces generated by external stimulations (except magnetic fields).In addition, the force due to the Brownian motion is not taken into consideration in the force analysis of microrobots in the flow, because it is notable only for particles whose radius is＜3 μm(Ahmed et al.,2021).

For helical microrobots and microswarms,in addition to all the forces mentioned above, the torque caused by the complex surrounding environment would also affect their motion in the flow.

3.1.1 Hydrodynamic drag forceFd

Hydrodynamic drag force (Fd) is the most important governing force for the motion of microrobots in the flow.The analysis ofFdis relatively non-straightforward.

For the simplified model,Fdis influenced by the following factors: the drag force coefficient (cd), the density of the flow(ρf),the projected surface area of the microrobot normal to the direction of its motion(A), and the relative velocity of the microrobot and the flow (vr), as shown in Eq.(5) (Sanchez et al.,2011; Arcese et al., 2012; Khalil et al., 2016; Sadelli et al., 2017; Demircali et al., 2021a, 2021b; Wang QQ et al., 2021):

The values ofρf,A, andvrare relatively easy to obtain, whereas the value ofcdis not.

Moreover, the calculation ofFdcould be more complex, if considering the wall effect, which means the impact of the blood vessel walls on the flow.

With ignorance of the wall effect and a deep simplification ofcdwhenRe →0 (cd≈24Re) (Nguyen-Van et al.,1994),the calculation ofFdhas been simplified as (Belharet et al., 2012; Khalil et al., 2016;Ahmed et al.,2021;Beaver et al., 2022)

As two important and complex influencing factors forFd,cdand the wall effect are discussed in detail below.

1.Drag force coefficientcd.Concluded from experimental observation and theoretical analysis,cdis influenced mainly by the shape of the microrobots and theRe(Tran-Cong et al., 2004; Tamaz et al., 2008; Choi J et al., 2010a, 2010b; Demircali et al., 2021a).For a microrobot, which has the surface-equivalent-sphere diameter ofdA, the volume-equivalent-sphere diameter ofdn(also called the nominal diameter), and shape factorc, within a flow withRe ＜2000,cdcan be calculated using Eq.(7) (Clift and Gauvin, 1970; Tran-Cong et al.,2004;Demircali et al., 2021a):

For a better understanding of the shape parameters of the microrobot,c,dA, anddnare explained in detail below.

cdenotes the surface sphericity and can be calculated with Eq.(8), wherePprepresents the projected perimeter of the microrobot in its direction of motion(Tran-Cong et al., 2004):

wheredArefers to the diameter of a sphere whose maximum cross-sectional area is the same as theAof the microrobot and can be calculated with Eq.(9).dnrefers to the diameter of a sphere whose geometric volume is the same as the geometric volumeVof the microrobot and can be calculated with Eq.(10).

As important parameters for calculating thecdof microrobots in the flow, bothdA/dnandchighly depend on the shape of the microrobot (Tran-Cong et al.,2004).

For a spherical microrobot, which is mostly studied in the literature (Martel et al., 2007;Arcese et al., 2012; Khalil et al., 2016; Meng et al., 2020;Demircali et al., 2021b), bothdAanddnrepresent the sphere’s diameter.Therefore,dA/dn= 1 andc= 1 (Tran-Cong et al., 2004).Correspondingly,the calculation ofcdcan be simplified as

In the literature, the most commonly used two calculation expressions ofcdfor sphere within a flow are Eq.(12) (Schiller and Naumann, 1933; Nguyen-Van et al.,1994;Demircali et al.,2021b)and Eq.(13)(White and Majdalani, 2006; Martel et al., 2007;Tamaz et al., 2008; Sadelli et al., 2017).These two formulae are directly obtained by fitting experimental results with different methods.

Although the expressions are different, there is no substantial difference among Eqs.(11),(12),and(13).The plots of these three formulas nearly overlap, as shown in Fig.4.

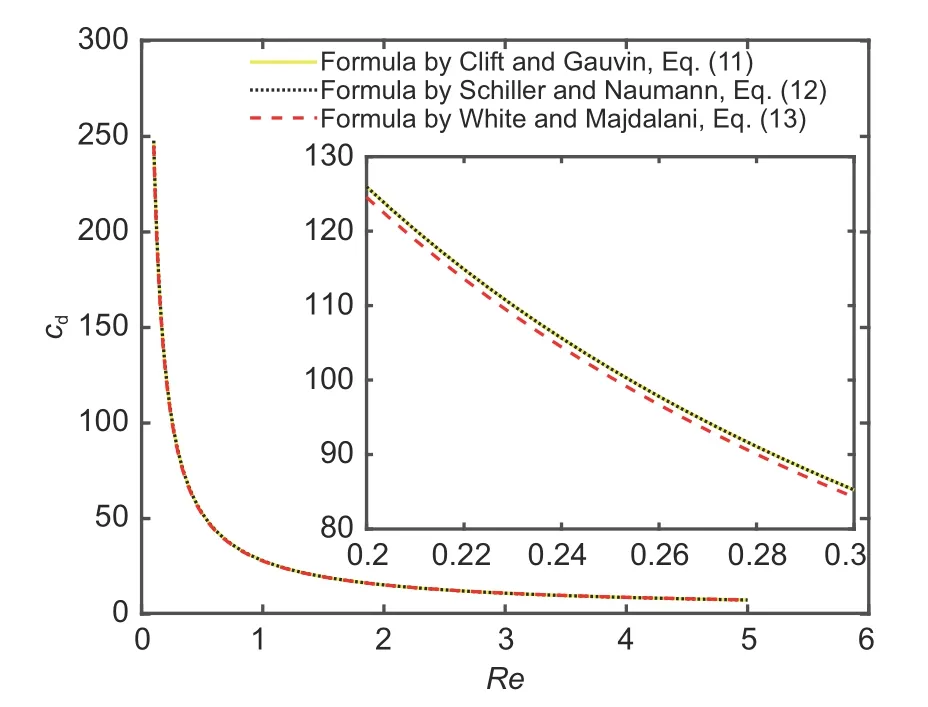
Fig.4 Plots of the drag force coefficients given by Eqs.(11)–(13)

As another important influentcing factor forcd,theReis decided based on the density of the liquidρf, the dimension of the microrobotd, the relative velocity between the microrobot and the flowvf,and the liquid viscosityμ, as shown in Eq.(14) (Tamaz et al., 2008; Demircali et al., 2021a).For spherical microrobots,drepresents the sphere diameter.

As blood flows in small vessels are non-Newtonian fluids, for which the shear stress is nonlinear to the shear strain rate,their viscosityμhas a nonlinear relationship with the vessel’s diameterDat a certain hematocrit ratehd, as shown in Fig.5(Arcese et al.,2012).

2.Wall effect.The wall effect refers to the influence of the blood vessel walls on the fluid in the vessel,which will consequently influence the drag force.This effect has been widely researched for spherical microrobots(Arcese et al.,2010a,2010b,2012).

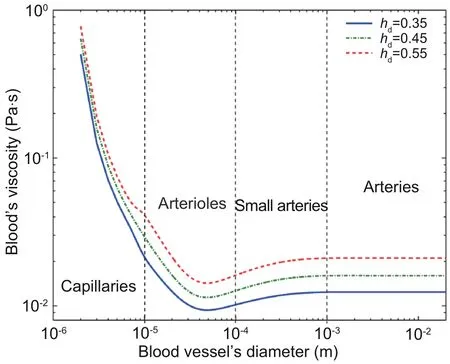
Fig.5 The non-Newtonian behavior in small vessels.Reprinted from Arcese et al.(2012), Copyright 2012,with permission from IEEE

Within a blood vessel, the velocity of the fluid has a parabolic profile.The flow rate near the vessel wall would be smaller than that at the center of the vessel,as shown in Fig.1a.Also,as the blood vessel constricts and relaxes while pulsating, the diameter of the blood vessel is time-varying (Arcese et al.,2012),resulting in a time-varying flow rate:

Here,wfandφfare the angular frequency and phase of the simplified model of the pulsatile flow respectively, which is a sinusoidal function of timet.Consequently, the relative velocity between the microrobot and the flow is dependent on space and time.The change of the relative velocity caused by the wall effect would induce the change ofcdandRe, as described in Eqs.(13) and (14).The change ofcdand the change of the relative velocity would both directly influenceFd, as described in Eq.(5).

The influence of the relative velocity change caused by the wall effect onFdhas been studied in many works (Kehlenbeck and Felice, 1999; Arcese et al., 2010a, 2010b, 2012).It has been proved that considering the wall effect, the relative velocity should be regulated with a coefficient, so that the calculation ofFdis modified as(Kehlenbeck and Felice, 1999;Arcese et al.,2012)

Hereλ=represents the ratio of the microrobot diameter(d)to the vessel diameter(D).Parametersα0andλ0should be functions ofRe.However,these two parameters are usually used with constant values of 1.5 and 0.29,respectively(Kehlenbeck and Felice,1999;Arcese et al., 2012).

3.1.2 Force caused by time-varying flowFd

Within a time-varying flow, the acceleration of the flow would cause pressure, so that a force (FQ)would be exerted on the microrobot (Khalil et al.,2016).This force will cause the microrobot to reduce its speed when it moves against the flow, and vice versa.Because the microrobot is small enough, its presence does not change the pressure distribution in the flow.Therefore, the pressure exerted on the microrobot would equal the pressure exerted on the flow occupied by the microrobot.The correspondingFQcould be calculated as

3.1.3 Contact forces

When his extreme hunger wakened him after several hours, he was still alone; but a little table, upon which was a good dinner, had been drawn up close to him, and, as he had eaten nothing for twenty-four hours, he lost no time in beginning his meal, hoping that he might soon have an opportunity of thanking his considerate entertainer, whoever it might be

Contact forces refer to the forces produced because of the impact between the microrobot and the wall, including the loading and unloading contact forces.The loading contact force happens from the moment when the microrobot starts to contact the wall to the moment when the maximum deformation of the wall occurs, whereas the unloading contact force happens from the moment when the wall has the maximum deformation to the moment when the microrobot loses contact with the wall(Choi IH and Lim, 2004;Arcese et al., 2012).

When there is no deformation of the wall, the contact force would be 0.When the deformation of the wall happens, contact forces occur, and loading and unloading contact forces can be calculated with Eqs.(18) and (19) (Choi IH and Lim, 2004; Arcese et al., 2012), respectively.Because the impact between the microrobot and the wall lasts only a few milliseconds (Hertzian contact law), the Heaviside step function could be used to describe the contact force.

wherekis the stiffness based on the microrobot and the blood vessel.nis the unit vector normal to the wall and pointing outside the vessel.δis the signed distance between the projection of the microrobot’s gravity center alongnonto the vessel wall at equilibrium and the projection onto the surface of the microrobot.δ0is the permanent deformation of the wall.δmis the maximum deformation of the wall.His the Heaviside step function.Fδmis the maximum contact force.Exponentpis based on local plastic deformation, the anisotropic properties of composite material, and the unloading rate (Tan and Sun,1985;Choi IH and Lim,2004;Arcese et al.,2012).

3.1.4 van der Waals and electrostatic forces

The van der Waals force refers to weak electrostatic force that attracts neutral molecules to one another, and ranges from interatomic spacings (about 0.2 nm) up to large distances (＞10 nm) (Zhang XJ,2013).This force is responsible for many important tribology-involved phenomena such as nanoscale friction, adhesion, surface tension, interfacial energy,physical adsorption, and wetting (Zhang XJ, 2013).The van der Waals force can be calculated from the differentiation of the van der Waals potentialVvdw,as shown in Eq.(20)(Arcese et al., 2012):whereAhis the Hamaker constant,h=|δ|/ris the normalized distance from the microrobot to the wall,andris the radius of the spherical microrobot.

The electrostatic force refers to the electric force for charged bodies at rest.The electrostatic force between the charged microrobot and the wall is given by (Arcese et al., 2012)

wherenis normal from the microrobot to the wall.In addition,q,ε0,andεare the microrobot’s charge,the vacuum permittivity,and the relative blood permittivity, respectively.The absolute value of electrostatic force decreases as the distanceδincreases(Arcese et al.,2012).

The van der Waals force and electrostatic force both become influential when the microrobot is close to the vessel wall(Arcese et al.,2012).When microrobots approach the wall, both the van der Waals force and electrostatic force dominate.When microrobots move away from the wall, the van der Waals force decreases rapidly, and the electrostatic force prevails(Arcese et al.,2012).

3.1.5 Other forces

Forces exerted on microrobots by external stimulations (except magnetic fields) are collectively called other forces here.These forces can regulate microrobot motion by adjusting microrobot position in the flow, instead of providing actuation or resistance directly,for example,acoustic radiation forces(Ahmed et al., 2021).

Because the flow rate near the wall is slower than that at the center of the vessel,it would be easy for a microswarm to move upstream along the wall.To achieve efficient upstream motion easily,acoustic fields were applied in Ahmed et al.(2021) to push the microswarm to the side of the vessel.When two acoustic fields with the same frequency are applied at the same time, the interference of two acoustic wavefield series will produce a series of nodes,where the minimum acoustic pressure exists.Due to the pressure gradient,the acoustic radiation force would be exerted on the microswarm to draw it close to the nodes.When a node is placed in the capillary(in the middle or on the sidewall), the microswarm will be trapped at the node’s position.When no node is placed in the capillary,the microswarm would be trapped against the sidewall, which is close to a node, because of the position restriction of the capillary.The switching of the trapping positions of the microswarm could be realized with two methods,modulating the resonant modes of the piezoelectric transducers (Fig.6a), or spatially shifting the position of the node by manually sweeping the excitation frequency(Fig.6b).

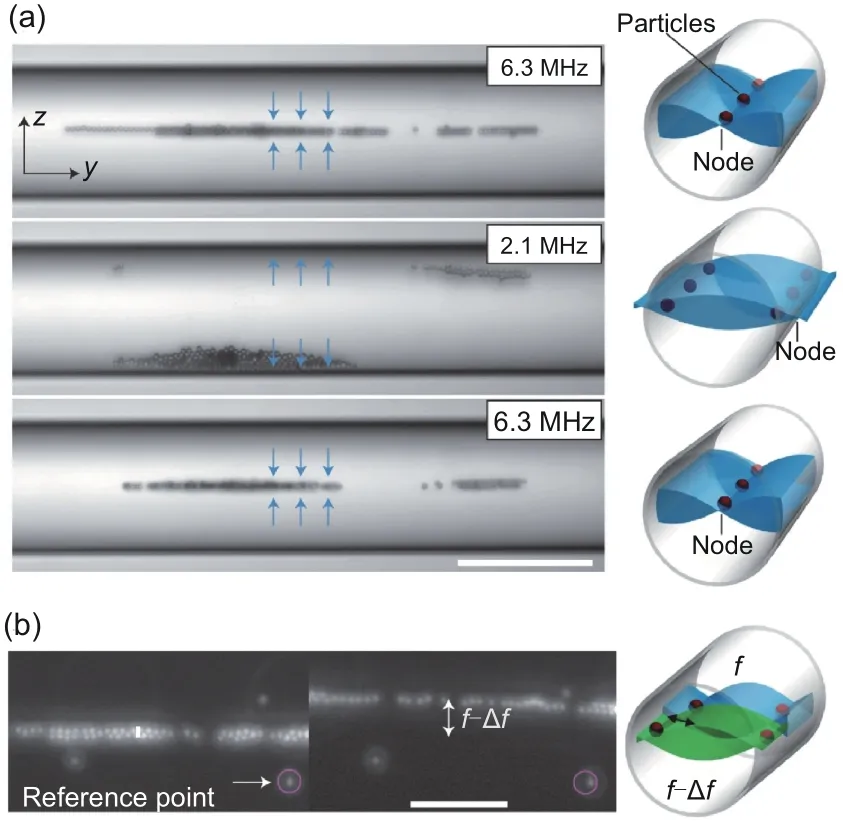
Fig.6 Change to a certain frequency (2.1 MHz) to push the microswarm to the sidewall (a) and spatial shift in the position of a node by manually sweeping the excitation frequency (b).Reprinted from Ahmed et al.(2021), Copyright 2021, with permission from Springer Nature

The acoustic radiation force also affects the upstream velocity of the microswarm (Ahmed et al.,2021).When the microswarm moves upstream in the vicinity of the sidewall, the minimum distance between the microswarm bottom and the capillary in the vertical direction (gap length) is decided by the acoustic radiation force.This is because,in the vertical direction,the lift force(dependent on gap length)and the constant gravity of the microswarm should be balanced with the acoustic radiation force.In the horizontal direction,the wet friction force(FWF)and the hydrodynamic drag force (Fd) balance each other, and these two forces are both dependent on the gap length.As explained in Eq.(5),Fdis related to the velocity of the microswarm.As a result of the balance equationFWF=Fd,the velocity of the microswarm robots is influenced by the gap length and is therefore affected by the acoustic radiation force.

3.1.6 Torque for helical microrobots

In addition to spherical and cylindrical microrobots, the motion of helical microrobots has been studied in the flow.Using helical microrobots for vascular occlusion treatment,in addition to studying helical microrobots’motion in a still liquid environment, Zhang HH et al.(2022) proved that their helical microrobots can swim against the flow through simulation (Fig.7).This simulation successfully presents a rough impression of the distribution of flow velocity with a moving helix.In some other works, the motion of helical microrobots swimming within the flow has been realized and studied.Acemoglu and Yesilyurt(2015)designed a helical microrobot with a magnetic head and studied the factors that influence its motion in the flow by simulations using the finite element method (FEM) and experiments.The agreement between simulation and experimental results is dependent on many factors,including the size of the channel, motion direction,magnetic field rotating frequency, and the distance between the microrobot and the channel wall.Liu et al.(2021) coated a soft helical microrobot (without head) withγ-Fe2O3nanoparticles and directed it against a flowing artificial biological fluid (phosphate buffer saline dispersed with polystyrene microspheres)stream.

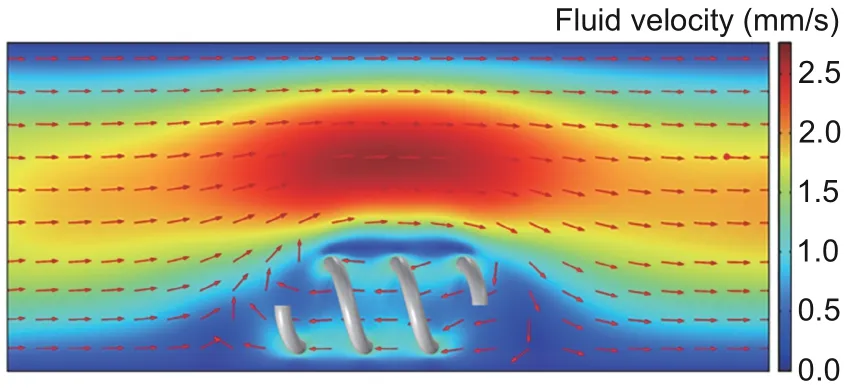
Fig.7 Simulated flow distribution as the microrobot moves in a 1-mm diameter channel against the flow where the average velocity is 1 mm/s.Reprinted from Zhang HH et al.(2022), Copyright 2022, with permission from the authors, licensed under CC BY 4.0

Although both rotating and gradient magnetic fields can propel helical microrobots, the motion studies of helical microrobots in the flow mostly focus on the motion actuated by rotating magnetic fields so far.Having only a rotating magnetic field as the propulsion source, the magnetic torque exerted on helical microrobots is used for actuation,while the magnetic force exerted on microrobots is 0.Accordingly, the resistant torque exerted on helical microrobots intends to prevent them from moving.Therefore,factors that influence torques would affect the motion of helical microrobots.

In Acemoglu and Yesilyurt(2015),the motion of a kind of helical microrobot in the flow(as illustrated in Fig.8) was analyzed and discussed in detail with both simulation and experiment.Tail length, tube diameter, flow rate, and direction of the rotation of the swimmer,which influence the magnetic torque or resistant torque, affected the velocity of the microrobot and the stability of its trajectory.When the microrobot moved toward its head, it had a helical trajectory, whereas the tip of the tail was closer to the center of the channel than the head.When the microrobot moved toward its tail,it started the motion with a reversed helical trajectory, and then the trajectory gradually stabilized on the central line of the channel.Although the flow direction did not influence the trajectories,the flow rate did.When the microrobot moved toward its head and against the flow,its velocity and the wavelength of its helical trajectory decreased as the flow rate increased,whereas the amplitude of the trajectory was not influenced by the flow rate.When the microrobot moved toward its tail and along the flow, the increase in the flow rate caused an increase in its velocity and delayed the stabilization of its trajectory.Moreover,microrobots with longer tails (the wavelength of the tailλwas kept unchanged)had smaller step-out frequencies.

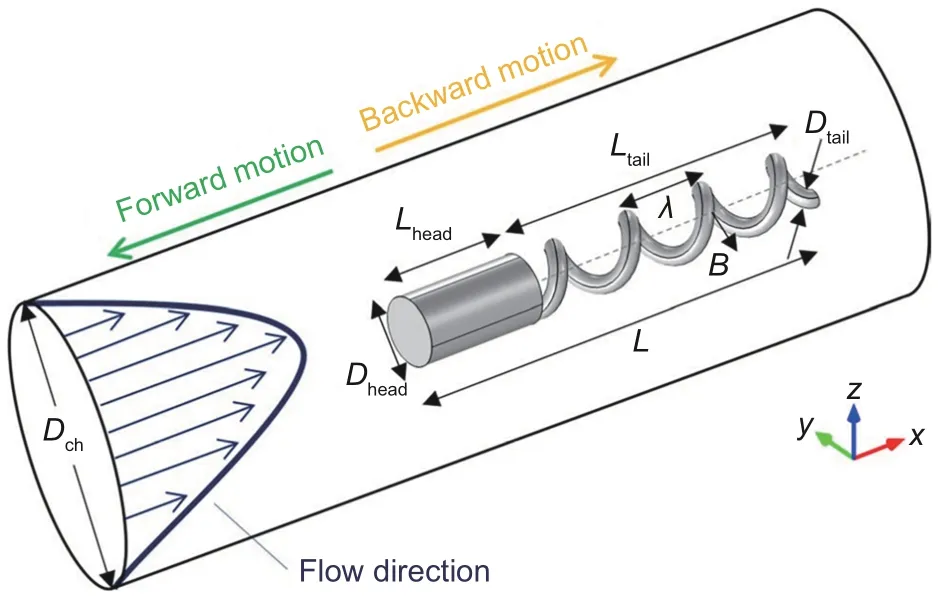
Fig.8 Structure of microrobot.Reprinted from Acemoglu and Yesilyurt (2015), Copyright 2015, with permission from Springer Nature

3.1.7 Theoretical analysis for microswarms

Magnetic microswarms have been a hot topic recently (Go et al., 2022; Xu ZC and Xu, 2022; Yang LD et al., 2022; Yue et al., 2022; Zhao et al., 2022),and some applications have been demonstrated,such as patching up microscale intestinal perforation(Yue et al.,2022)and chemoembolization(Go et al.,2022;Law et al., 2022).The dynamic modeling of microswarms is different from that of a single microrobot because the interaction forces within the swarm should be considered.The interaction between magnetic microrobots within a swarm enables the dynamic formation of complex patterns.In the recent literature (Yu et al., 2019; Wang QQ and Zhang, 2021), magnetic microswarms were categorized into three types based on their governing formation mechanisms,including magnetic-interactioninduced swarms, hydrodynamic-interaction-induced swarms, and weakly interacting swarms.Magneticinteraction-induced swarms are formed based on the magnetic interaction within the swarms,and the pattern of this kind of swarm could be controlled by the input magnetic field.Hydrodynamic-interactioninduced swarms are formed based on interaction exerted through the hydrodynamic flow and the interface.These swarms are vortex-like swarms and their sizes are governed by the inner interactions between the core region and the surrounding microrobots.For weakly interacting swarms, the interactions between microrobots are too weak, and their motion would not affect each other.The detailed dynamic modeling and force analysis of each swarm type can be found in Wang QQ and Zhang(2021).

As discussed above, many factors influence the motion of microrobots in the flow,including cylindrical microrobots, spherical microrobots, helical microrobots, and microswarms.Most of these factors can be modeled to understand the corresponding motion theory.As modeling simplifies the actual cases,the disturbance would always exist and should be considered in control strategies.

3.2 Theoretical models vs.experiments of microrobots in a flow

Considering comprehensively all the forces and influential factors mentioned above that could be exerted on microrobots, the motion and state for specific microrobot cases in the flow have been simulated based on theoretical models in some recent works (Acemoglu and Yesilyurt, 2015; Li JY et al.,2018;Demircali et al.,2021a;Wu et al.,2022).Theoretical models and simulations based on theoretical analysis could help the understanding and guide the manipulation experiments of microrobots in the flow, although they might have slight differences with experimental results.For example, Demircali et al.(2021a) proposed a permanent-magnet-based micromanipulation method to enable the positioning and locomotion of a microrobot in laminar flow settings.The microrobot motion characteristics(displacement) at different flow rates were theoretically analyzed,simulated,and observed with experiments.In the theoretical analysis, drag force and magnetic force were calculated to obtain the dynamic motion model of the microrobot’s longitudinal motion.Using an FEM-based program COMSOL, the microrobot motion was simulated.Using the proposed setup, experiments were conducted to analyze the microrobot’s longitudinal motion in the laminar flow regime.A comparison of analytical results, FEM simulation, and experimental results of this work is shown in Table 1.It is confirmed that theoretical analysis and simulation could represent the experimental results to a certain extent (Demircali et al.,2021a).

4 Control strategies and methods

So far, the strategies of both open-loop control and closed-loop control have been used for the motion control of microrobots in the flow,stabilizing microrobot positions,helping microrobots move following particular trajectories,and improving the robustness of microrobot motion.The open-loop control strategy is widely used in microrobot control systems with low precision(Khalil et al.,2016;Ahmed et al.,2021;Demircali et al.,2021a).For more precise and automatic control of microrobots in the flow,closedloop control strategies have been used,including PID control (Choi J et al., 2010a; Khalil et al., 2014a,2016), MPC (Belharet et al., 2011, 2012), backstepping control (Arcese et al., 2012), and ESO-based model-free control(Meng et al.,2020).Among these strategies and methods,open-loop control,PID,and MPC are the most commonly used.Both open-loop control and PID are straightforward, whereas the implementation of PID needs proportional,integral,and derivative parameter adjustments.As a relatively complicated control method, MPC considers the state constraints and constraints of the control signal.In the following, the control methods used for the motion control of microrobots in a flow are introduced.

Table 1 Displacement values under the analytical calculations from simulation results and experimental measurements, and error values in comparison with the experimental results at different flow rates from 1.0 to 4.5 mL/min

4.1 Open-loop control

With open-loop control, input is set and adjusted without considering sensory feedback (Zhang ZG et al., 2008).This control strategy is convenient but inadequate when a disturbance occurs or when the model is imprecise.Drag force compensation is a robust way to reduce the effect of disturbances.Regarding the motion control of magnetic microrobots in a flow, the open-loop control strategy has been applied in many studies (Tamaz et al., 2008; Choi J et al., 2010a, 2010b; Mathieu and Martel, 2010;Sanchez et al., 2011; Acemoglu and Yesilyurt, 2015;Khalil et al., 2016; Ahmed et al., 2021; Demircali et al., 2021a; Beaver et al., 2022).By adjusting the position of permanent magnets or adjusting the current within the electromagnets, designed magnetic fields are generated to control the motion of magnetic microrobots.

In Mathieu and Martel (2010), a Maxwell pair was used to guide the movement of microrobots with open-loop control.By controlling the currents within the Maxwell pair,gradient magnetic fields were generated to steer the microrobots within a Poiseuille flow of 1.05 m/s.With higher magnetic field gradients,which can be realized by increasing the current,more microrobots would be steered at the branch of the channel (Fig.9a).In Khalil et al.(2016),open-loop control was used to actuate the motion of microrobots in a time-varying flow.With an increase in the magnetic field gradient or decrease in the flow rate, the average speed of the microrobots is increased, as shown in (Fig.9b).In Demircali et al.(2021a),open-loop control for moving a microrobot toward a targeted position within flows with certain flow rates was realized.After the targeted position was reached,microrobot oscillation was observed.The oscillation amplitude is highly related to the flow speed.

By applying constant direct currents (DC) to a magnetic field generator that consists of a pair of Maxwell coils and a pair of Helmholtz coils, Choi J et al.(2010a) realized position stabilization of microrobots in both a vascular phantom with a onedimensional (1D) pulsating flow and the aorta of a pig with open-loop control.Using feedforward current input generated by a pressure transducer in the open-loop control, the fluctuation of the microrobots was reduced as the drag force was compensated for.However, because the open-loop control with feedforward input still lacks feedback on the microrobot positions, the microrobots still fluctuated obviously along with the waveform of the pulsatile flow.Fig.9c shows the performance of DC open-loop control with and without feedforward input for position stabilization of microrobots.With the same system and open-loop control methods,movements of microrobots in a vascular phantom with a 1D pulsating flow and in the aorta of a pig were realized, and the fluctuation was evaluated(Choi J et al., 2010b).

Using optimization methods to minimize or maximize an objective function, optimal open-loop control can be realized(Kalman et al., 1960;Naidu,2002;Pršić et al.,2017).In Khalil et al.(2016),with optimal open-loop control,the navigation path with the minimum energy between two fixed points was first obtained by calculus with variations.Then,targeted navigation of microrobots with the minimum energy was realized based on the calculation results.As shown in Fig.9d, the path with the minimum energy obtained from the calculation has a parabolic profile, which is consistent with the fact that the flow rate decreases from the center to the edges of the channel.

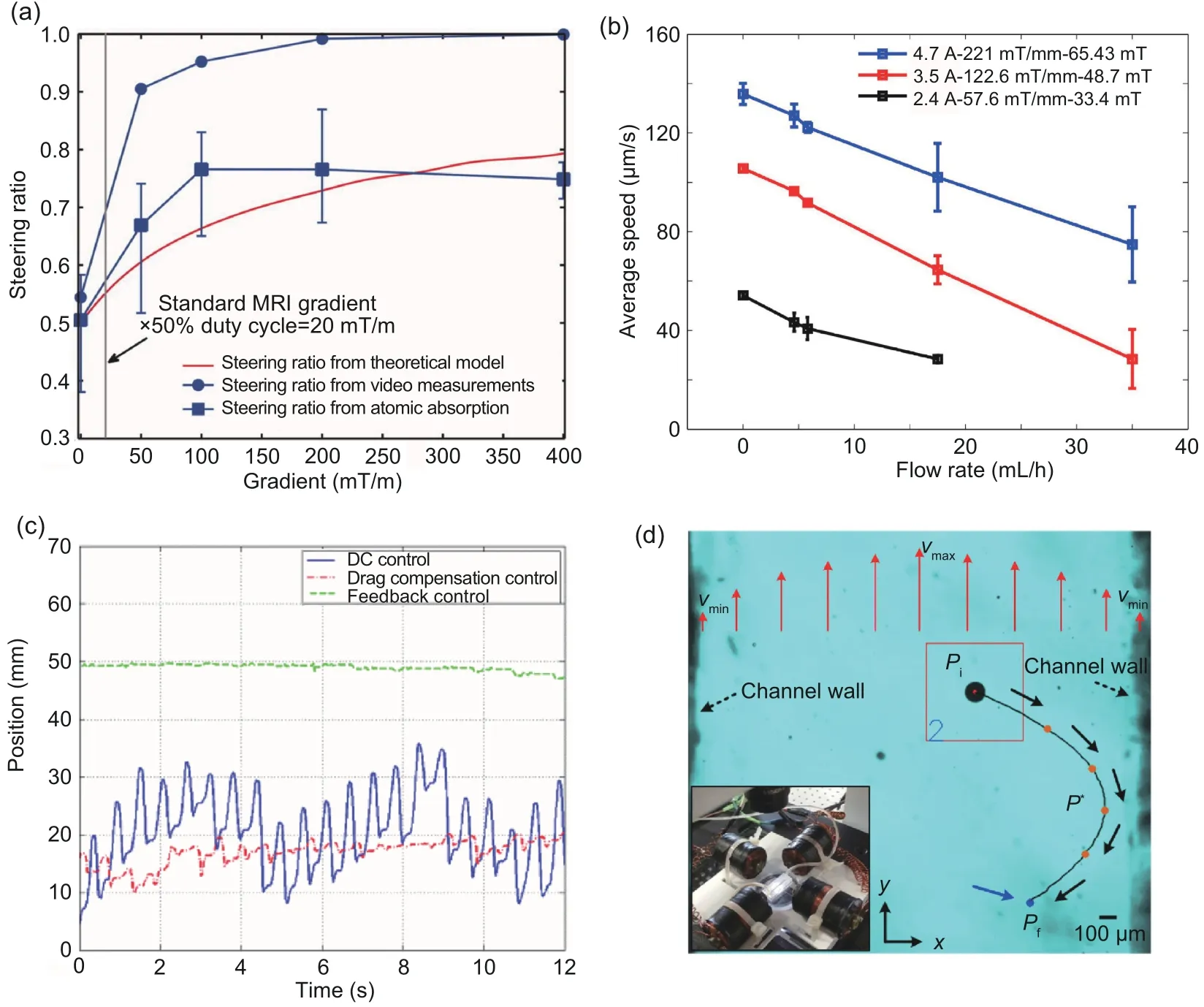
Fig.9 (a) Steering ratio under different gradient magnetic fields; (b) speed of the microrobot under different flow rates; (c) microrobot positions under DC, DC with drag force compensation (feedforward), and PID; (d)optimal path from one point to another.(a) is reprinted from Mathieu and Martel (2010), Copyright 2010,with permission from John Wiley and Sons; (b) and (d) are reprinted from Khalil et al.(2016), Copyright 2016, with permission from the authors, licensed under CC BY 3.0; (c) is reprinted from Choi J et al.(2010a),Copyright 2010, with permission from IEEE

Moreover, open-loop control is the only control method that has been used to navigate swarm microrobots within the flow so far(Wang B et al.,2018;Ji et al.,2020;Jarvis et al.,2022;Yang SH et al.,2022).In Yang SH et al.(2022),pattern transformation was realized by manually controlling the magnetic field.The microrobots can maintain the swarm pattern while they move downstream/upstream at the same time.Also, the flow has no significant influence on the control of pattern transformation, because the elongation and shrinkage rate of the microswarm in dynamic flow are similar to that in stagnant fluids.Pseudo bang-bang control, as a type of optimal open-loop control,has also been used to control microswarms.In Jarvis et al.(2022),bang-bang control allows a quick change of magnetic field gradient rather than fine tuning.

4.2 PID control

As a typical closed-loop control method, PID control is conducted using the proportion (P), integral (I), or derivative (D) of the error signals as the feedback to the input (Ang et al., 2005).It is most widely used for its simplicity and precision,but it is not good at dealing with systems with state coupling, strong nonlinearity, or significant external disturbances (Hu B et al., 2013; Jiang et al., 2022).Although fuzzy PID and adaptive PID can solve nonlinear problems, parameter adjustment within these two methods is complicated(Li YB and Song,2012).Regarding the motion control of magnetic microrobots within a flow, PID control, which is more precise than open-loop control, has been used in many works(Tamaz et al.,2008;Choi J et al.,2010a,2010b;Khalil et al.,2014a,2016).

Using the position information obtained from the CMOS camera visual system as the feedback signal, PID control for positional stabilization of microrobots with small errors in a pulsating flow was realized by Choi J et al.(2010a).At the position of 30 mm in thex-axis, the fluctuation range of the error was reduced to 1/8 compared to openloop control and 1/4 compared to open-loop control with feedforward input.With the same actuation and visual feedback systems, Choi J et al.(2010b)conducted PID control with drag force composition for the movement of microrobots in a pulsating flow(Fig.9c).In Tamaz et al.(2008), position information received by the magnetic resonance imaging(MRI)tracking system was used as the feedback signal to achieve PID control of microrobots in a pulsatile flow.The MRI system was also used to propel the microrobots.To achieve the targeted motion of chemically powered microrobots along or against the flow with the direction guide of a magnetic field,PD control was used by Khalil et al.(2014a)with visual feedback.With PD control,microrobots with a certain velocity within a circular region of convergence(ROC) at the targeted location could be achieved.The ROC would expand with an increase in the flow rate (Fig.10a).In Khalil et al.(2016), PD control was used for motion control of magnetic microrobots against the flow.The results showed that the steady error would increase with an increase in the flow rate.To deal with the cases in which the flow rate suddenly increased, PD control with a disturbance observer was used to improve the transient- and steady-state characteristics(Fig.10b).

4.3 Model predictive control

MPC refers to a wide range of control methods that use a model to obtain the control signal by minimizing an objective function (Camacho and Bordons,2007).Compared to PID, which is usually model-free, MPC is model-based and considers constraints.MPC is useful for multi-input multi-output systems,but it requires more calculations than PID.

Fig.10 Precision of the position was measured by a circle around the 2D position and the circle has a diameter of 190 μm under PD control (a) and dynamic response of positions and current in the x- and y-axis with a sudden change of flow rates(b).(a)is reprinted from Khalil et al.(2014a), Copyright 2014, with permission from IEEE; (b) is reprinted from Khalil et al.(2016),Copyright 2016, with permission from the authors, licensed under CC BY 3.0

As a typical example,Belharet et al.(2011)designed an MPC controller embedded with a low-level robust controller to navigate a ferromagnetic microrobot in vessels.The embedding of the low-level robust controller is used to provide robustness against the flow,noise,etc.Based on the image of vessels and the microrobot,the reference trajectory and the position of the microrobot were obtained.Then the error between the trajectory and position at this stage was calculated and put into the MPC optimizer.The MPC optimizer would generate the predicted future inputs, which would then be fed into the model for the next loop of the procedures.As the final control effect, the error between the real positions and the trajectory would increase with an increase inNwhenN ≥10, but it would not be affected by the change inNwhenN ＜10.By increasing the duty circle(working_time/total_time)of the MRI,which is used for both propulsion and visualization of the microrobots,the error would become smaller.

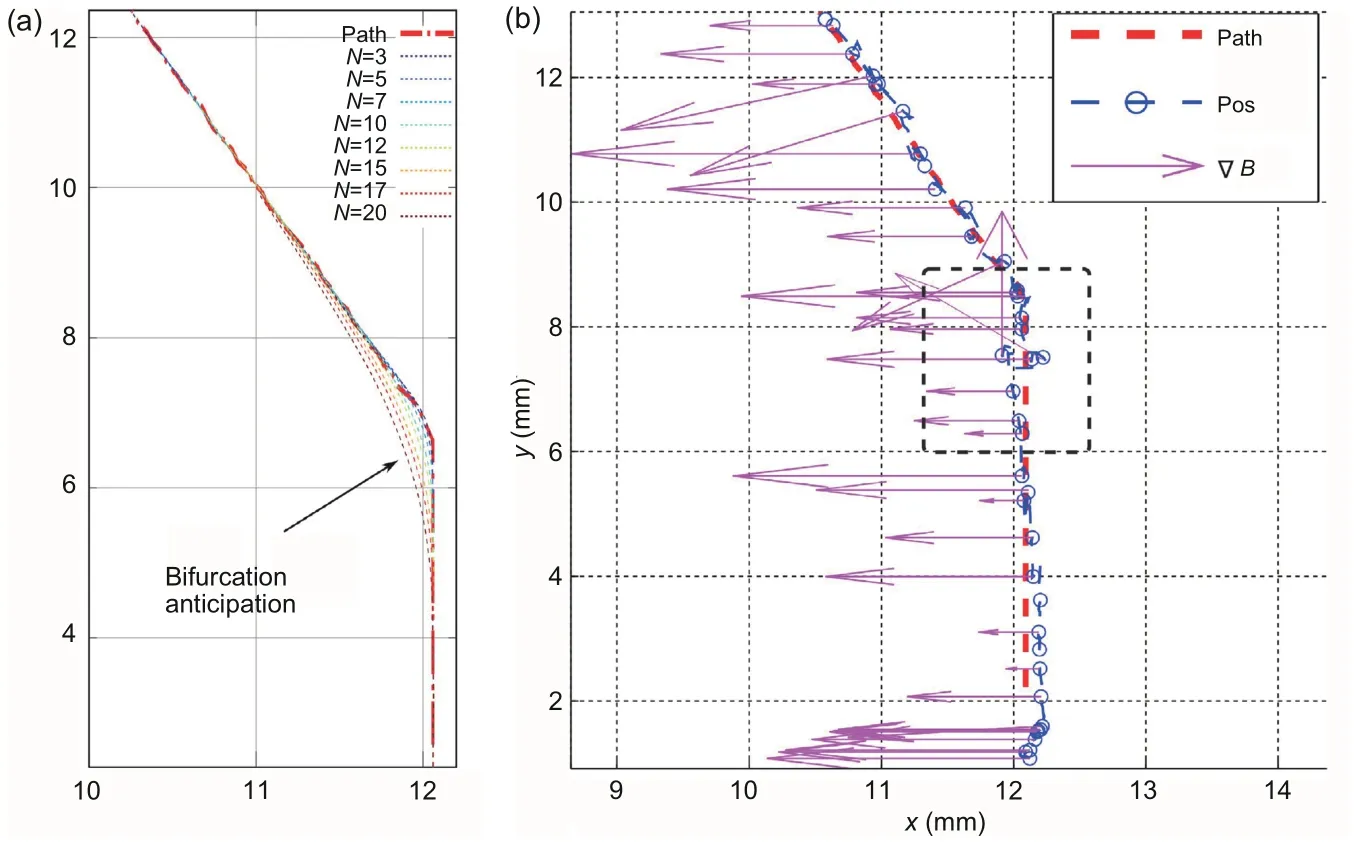
Fig.11 Path tracking using generalized predictive control (GPC) with pulsatile flow: (a) simulation; (b)experiment with GPC prediction horizon N=10.Reprinted from Belharet et al.(2012), Copyright 2012, with permission from IEEE

As one of the most popular MPC methods,generalized predictive control (GPC) is also used in the motion control of microrobots.In Belharet et al.(2012), GPC was used for microrobot motion control in pulsatile flows with bifurcation.In this work, the microrobots were actuated by a 3D gradient magnetic field generated by three pairs of Maxwell coils, with visual feedback.The optimization part of GPC was obtained by minimizing the following criterion:

where ˆy(t+j)is the optimum predicted output of the system at timet+j,P(t+j)is the future reference trace,N(＞0)defines the size of the prediction horizon,δis the same as that in Eqs.(18) and (19),andλ ＞0 is the control weighting.Based on the optimization result, the future control input can be calculated from ˆy(t+j).The input is returned to the model to obtain the real future output.Then the future output is used to calculate the input for the next step.To demonstrate GPC in this work, simulation and experiments were conducted.The simulation was done with a 1D systolic pulsatile flow as the application scenario.The simulation results showed that the path behavior was over-anticipated when prediction horizonNwas large, especially at the bifurcations.Based on the simulation results,GPC was implemented with experiments in pulsatile flow and the controller remained robust.Nand the constitution of the flow influenced the path-tracking error.The results proved that the experiment could basically follow the simulation, although the error still existed(Fig.11)(Belharet et al.,2012).

GPC uses an inversing matrix operation that requires much online calculation and is thus hard to apply in a situation with a high flow rate (Meng et al.,2020).

4.4 Backstepping control

Backstepping control simplifies a complex nonlinear system to multiple subsystems whose order is not larger than that of the original system.It uses the high-order output as the virtual input of the low-order system.Then a Lyapunov function is built based on the low-order system to gain stability.These steps are repeated until the lowestorder system is reached, which results in the final real input.Using the Lyapunov function to keep the system stable all the time, a reference input is calculated and used for the design of the input (Arcese et al., 2012; Sadelli et al., 2017).Backstepping control is frequently used in output regulation problems.However, the formulation for this control method is complex.

Using backstepping control,Arcese et al.(2012)simulated the motion control of magnetic microrobots within a small artery.Despite noise measurement and modeling errors,efficient tracking can still be realized.

4.5 ESO-based model-free control

Model-free control refers to the control methods without the physical model (Fliess and Join, 2013).It is used for cases where the model is difficult to obtain.The complexity of the calculation for this control method limits the applications.

Using an ESO-based model-free control proposed by themselves, Meng et al.(2020) simulated the motion control of a magnetic microbead in a blood vessel with bifurcation, without any knowledge of the blood-velocity distribution.In this work,the proposed ESO-based model-free controller combines sliding mode control,backstepping control,and disturbance compensation.As a reference for comparison, an active disturbance rejection controller(ADRC)with ESO was used in this work.As shown in the control block (Fig.12), the introduction of ESO into the control system can observe noises and disturbances efficiently so that the control is more precise.

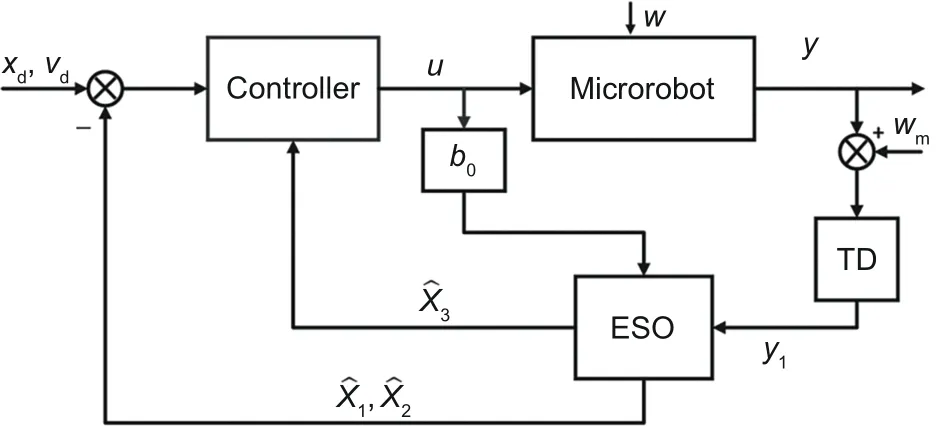
Fig.12 Control diagram of the proposed ESO-based model-free control.Reprinted from Meng et al.(2020), Copyright 2020, with permission from IEEE

5 Potential applications of magnetic microrobot control within a flow

Magnetic microrobots have shown great potential for biomedical applications,such as embolization and drug delivery (Go et al., 2022;Law et al., 2022;Oral and Pumera,2023).With the knowledge of microrobot motion in a flow, some applications have been realized.For example, in Go et al.(2022), a swarm of microrobots was guided by magnetic field towards a targeted area in a liver blood vessel to realize chemoembolization.Then,with the proper use of suitable control methods for microrobots within the flow, much precise navigation of microrobots could be realized.In Jia et al.(2022), a microrobot was navigated by electromagnetic fields within the yolk of a zebrafish embryo.A robust controller that integrates adaptive sliding mode control(ASMC) and a nonlinear disturbance observer was proposed to ensure the stability and accuracy of the microrobot motion.In the future,in-depth understanding of microrobots in complex flow environments and extensive application of advanced control methods would significantly improve the accuracy and efficiency of the clinical use of microrobots.

6 Conclusions and outlook

This review summarizes state-of-the-art research on magnetic microrobots moving in the flow,including establishing flow systems, dynamics modeling of microrobot motion,and commonly used control methods.In the section on flow systems, commonly used flow types (Poiseuille flow and pulsatile flow)are first introduced.The flow systems are categorized into four types based on their resemblance to human vessels.Some typical examples of each type are discussed in detail.In the section on dynamics modeling of microrobot motion, magnetic actuation force/torque and different kinds of resistance forces and their influencing factors are discussed in detail.As a special case, helical microrobot modeling was discussed separately.In the section on control methods, the commonly used control methods for microrobot motion in the flow (including openloop control, PID, MPC, backstepping control, and ESO-based model-free control) are introduced and discussed with some examples.Although many studies have been conducted, as summarized in this review, microrobot motion in the flow still has several challenges.The flow systems should be further developed for more resemblance to the actual case.Accordingly, for the more complex systems, dynamics modeling should be developed to be more accurate.Image-based tracking and control of microrobots in vivo need further study.For visualization of microrobots in vivo, photoacoustic technology may be the next option (Xu MH and Wang, 2006).Moreover, the controller should be developed to be more robust to disturbance from the blood flow.In summary, the motion of microrobots in the flow is very important for realizing clinical uses of microrobots.The corresponding studies can still be improved in three aspects in the future, i.e., inventing more human-like flow systems for the studies, achieving more accurate dynamics models,and developing advanced imaging and control methods,including more powerful disturbance estimation and compensation methods.

Contributors

Jiamiao MIAO summarized the literature and drafted the paper.Xiaopu WANG and Huihuan QIAN formulated the research goal and outlined the paper.Yan ZHOU, Min YE, and Hongyu ZHAO revised Sections 2 and 3.Hongyu ZHAO and Ruoyu XU revised Section 4.Jiamiao MIAO,Xiaopu WANG, and Huihuan QIAN revised and finalized the paper.

Compliance with ethics guidelines

Huihuan QIAN is a corresponding expert ofFrontiers of Information Technology&Electronic Engineering, and he was not involved with the peer review process of this paper.All the authors declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request.