A hybrid-model optimization algorithm based on the Gaussian process and particle swarm optimization for mixed-variable CNN hyperparameter automatic search*
Han YAN, Chongquan ZHONG, Yuhu WU, Liyong ZHANG, Wei LU
School of Control Science and Engineering, Dalian University of Technology, Dalian 116024, China
†E-mail: luwei@dlut.edu.cn
Abstract: Convolutional neural networks (CNNs) have been developed quickly in many real-world fields.However,CNN’s performance depends heavily on its hyperparameters, while finding suitable hyperparameters for CNNs working in application fields is challenging for three reasons: (1)the problem of mixed-variable encoding for different types of hyperparameters in CNNs, (2) expensive computational costs in evaluating candidate hyperparameter configuration, and (3) the problem of ensuring convergence rates and model performance during hyperparameter search.To overcome these problems and challenges, a hybrid-model optimization algorithm is proposed in this paper to search suitable hyperparameter configurations automatically based on the Gaussian process and particle swarm optimization (GPPSO) algorithm.First, a new encoding method is designed to efficiently deal with the CNN hyperparameter mixed-variable problem.Second, a hybrid-surrogate-assisted model is proposed to reduce the high cost of evaluating candidate hyperparameter configurations.Third, a novel activation function is suggested to improve the model performance and ensure the convergence rate.Intensive experiments are performed on imageclassification benchmark datasets to demonstrate the superior performance of GPPSO over state-of-the-art methods.Moreover, a case study on metal fracture diagnosis is carried out to evaluate the GPPSO algorithm performance in practical applications.Experimental results demonstrate the effectiveness and efficiency of GPPSO, achieving accuracy of 95.26% and 76.36% only through 0.04 and 1.70 GPU days on the CIFAR-10 and CIFAR-100 datasets,respectively.
Key words: Convolutional neural network; Gaussian process; Hybrid model; Hyperparameter optimization;Mixed-variable; Particle swarm optimization https://doi.org/10.1631/FITEE.2200515 CLC number: TP181
1 Introduction
In recent years, as one of the most useful deep learning models,convolutional neural networks(CNNs)have achieved state-of-the-art results in various artificial intelligence (AI) applications (Jiang and Luo,2022;Tulbure et al.,2022).Through convolution operations,meaningful features are extracted from input data,which have greatly improved model performance (Sun et al., 2019).Such learning and expression abilities result in great success in various real-world applications, such as face detection(Li X et al., 2022) and autonomous driving (Grigorescu et al., 2020).Although CNNs have achieved great success,the design of CNN architecture is still extremely complicated,and obtaining efficient CNN models for solving specific tasks is still a challenge(Fernandes and Yen, 2021; Guo et al., 2022).Furthermore, most efficient CNN models are designed and optimized by experienced AI algorithm engineers through tedious trial-and-error experiments,which does not help technicians in other industries who want to use AI technology.
Therefore, many researchers have started to consider designing CNN models in a more intelligent,automatic,and efficient way(Li JY et al.,2022).For example, to realize automation in the model design process, researchers regarded the process as an optimization problem, and found the optimal solution using intelligent algorithms(Zhan et al.,2022a).Intelligent optimization algorithms(OAs)are regarded as a class of methods of deriving optimal solutions that have been extensively researched, such as using Bayesian optimization(BO)(Snoek et al.,2012),particle swarm optimization(PSO)(Poli et al.,2007;Li JY et al.,2021),and other evolutionary computation(EC)approaches(Li JY et al.,2020;Zhan et al.,2022b; Wu SH et al., 2023).As an application of the Gaussian process(GP)in optimization problems,BO has been proposed to optimize search hyperparameters in machine learning algorithms.Snoek et al.(2012) selected expected improvement (EI) as the acquisition function to optimize three typical machine learning problems,which reduced training cost and improved training speed.Jin et al.(2019) used BO to guide the generation of network morphism for automatic construction of CNN models, and a new GP kernel function was designed according to the characteristics of network morphism exploration space.Li JY et al.(2023) proposed a surrogateassisted hybrid model to optimize CNN’s hyperparameters,where GP was used as a surrogate model to estimate the fitness function to save computational cost.Li JY et al.(2022) and Zhan et al.(2022a)used BO to search different combinations of hyperparameters to construct different architectures.The unique properties of BO can reduce the number of trained neural networks,resulting in a more efficient search process.As a branch of EC, PSO is efficient to find optimal solutions to high-complexity problems due to its wide exploration area and fast convergence (Li JY et al., 2022).For instance, Wang B et al.(2018) proposed a variable-length encoding method for CNNs and searched hyperparameters through PSO to optimize CNNs, whereas Fielding et al.(2019) used a PSO algorithm and ensemble learning to automatically design CNNs.Wu T et al.(2019) treated model pruning as a multi-objective problem and solved it by PSO to balance the accuracy and complexity, which can reduce weights by 80% without losing significant accuracy.Wang B et al.(2020)proposed an efficient PSO(EPSOCNN)method inspired by transfer learning to accelerate search process, which reduced the search space and demonstrated the transferability of the evolved block.Wang YQ et al.(2022) designed a novel and light-weight scale-adaptive fitness evaluation-based PSO method for reducing search time and providing search performance.In addition, some other EC algorithms can achieve better results in cooperation with model optimization(Alvarez-Rodriguez et al., 2021; Chen et al., 2022).Real et al.(2017)proposed a large-scale neuro-evolutionary method to discover the best CNN model, and achieved 94.6%and 77.0% accuracy on CIFAR-10 and CIFAR-100,respectively.Sun et al.(2020a) used a novel genetic algorithm(GA)called CNN-GA to search CNN architecture automatically.These algorithms have achieved promising results in CNN hyperparameter optimization tasks.
However,there are still some challenges for CNN hyperparameter optimization tasks due to following problems: mixed-value hyperparameter encoding, high computational cost, low convergence rate,and limited model performance.First, the CNN hyperparameter types are different (continuous or discrete) (Darwish et al., 2020), and such mixedvariable characteristics are proved difficult in effi-cient search space encoding.Second, for traditional OAs(BO and PSO), CNNs are evaluated by the fitness function through assessment criteria based on training, which increases the cost of fitness evaluation(FE)and damages the efficiency of OAs.Third,considering the large number of CNN hyperparameters,it is still necessary to research how to accelerate the convergence for FE and ensure model performance after search.
Therefore,in this paper we focus on these challenging tasks in the CNN hyperparameter optimization problem and propose a novel Gaussian process and particle swarm optimization (GPPSO) method based on GP and PSO,to solve these difficulties.The major challenges and contributions are summarized in Fig.1.

Fig.1 Major challenges and contributions of GPPSO
1.A novel encoding strategy is proposed to efficiently deal with the mixed-variable difficulty of CNN hyperparameters.A unified encoding strategy is designed to encode discrete and continuous variables in the same form,making the optimization process more efficient.
2.A hybrid-surrogate-assisted(HSA) model is proposed to deal with the expensive computational cost problem in the search process.During the search process, the GP model serves as a surrogate for the fitness function, while the PSO algorithm generates new individuals.To achieve a better balance between efficiency and performance,a multi-level evaluation mechanism is proposed to reduce computational cost.
3.A novel activation function(AF,Ta-ReLU)is proposed to accelerate the convergence in the process of population evolution and to improve the performance of the model after training.The improved AF has a tiny gradient in the region(<0),which not only enhances the model’s performance, but also ensures efficient training.
2 Background and related works
The concepts of CNN, Gaussian process regression (GPR), and PSO as the basic algorithms of GPPSO are introduced in Sections 2.1, 2.2,and 2.3,respectively,which are helpful to know the details of the proposed GPPSO.
2.1 Convolutional neural network (CNN)
CNN is a type of deep feedforward neural network that has the advantages of local links and weight sharing (Alzubaidi et al., 2021).With the development of CNNs, the network structures have gradually become deeper, and VGGNet and ResNet have emerged as two state-of-the-art CNN structures in recent years.
VGGNet (Simonyan and Zisserman, 2014) is a frequently employed CNN for extracting features.Fig.2 illustrates a 16-layer version of VGGNet, consisting of 13 Conv layers and three fully connected(FC) layers.Because smaller 3×3 Conv kernels are used to simulate 5×5 Conv kernels, VGGNet can obtain larger receptive fields with fewer parameters,resulting in effective and efficient feature extraction.
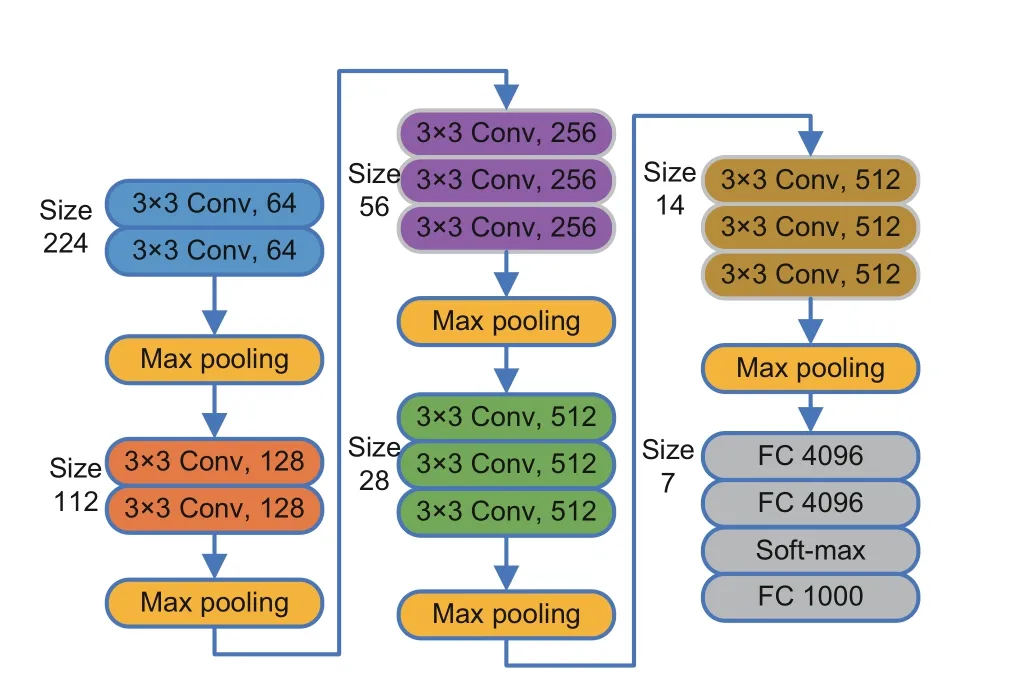
Fig.2 VGG16 model structure
ResNet (He et al., 2016) is another commonly used residual structure CNN for feature extraction.ResNet used cross-layer connections to fit residual items, which extends the depth of CNNs.The residual block is shown in Fig.3a, which outputsy=F(x) +xafter the input passes through the module.The overall structure of ResNet is shown in Fig.3b.
Based on their effective characteristics,VGGNet and ResNet are chosen as basic models for the proposed algorithm.
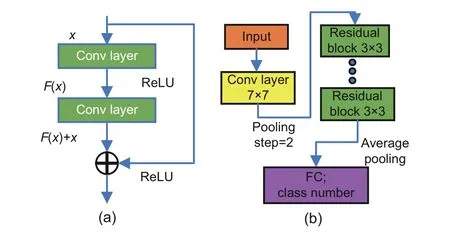
Fig.3 ResNet model structure: (a) residual block;(b) ResNet
2.2 Gaussian process regression(GPR)
Gaussian process regression (GPR) is an effi-cient modeling algorithm based on statistical learning theory.In contrast to parameterized models in machine learning (e.g., Bayesian linear regression),GP is a nonparameterized model that can fit a black box function and give confidence in the fitting results.In GPR, it is assumed that an unknown functionf(x) is smooth and follows a GP.WhenNpointsX=[x1,x2,···,xN]are sampled fromf(x),the resulting dataset follows a multivariate normal distribution as shown in Eq.(1):

whereK(x*,X) = [k(x*,x1),k(x*,x2),···,k(x*,xn)].According to the above joint distribution, the posterior distribution ofy*, mean ˆµ, and variance value ˆσ2are calculated as follows:
Based on the above properties,GPR is employed as a surrogate-assisted model to predict the performance of the model in this study.
2.3 Particle swarm optimization(PSO)
PSO is a type of EC approach based on artificial life and evolutionary computing theory.The main procedures of PSO are as follows: first, PSO initializes a population of individuals with positionX0iand speedV0i,where each individual corresponds to a random candidate solution to the object function.Then, based on the fitness value, individual extremum pbest and global extremum gbest are updated using Eqs.(7)and(8):
wherevidandxidrefer to thedthvelocity component and position component of theithparticle of thekthgeneration respectively, andc1andc2are learning rates, which control the amplitude of evolution to the individual best particle and the global best particle respectively.The above procedures will be repeated until the expected error value is reached or the maximum number of iterations is reached.Finally, the PSO outputs the best position of the particle, which corresponds to the optimal solution to the problem.Due to its ease of implementation and minimal tunable parameters,PSO can be a good choice for solving complex optimization problems in CNNs, and is also a basic algorithm of GPPSO.
3 Proposed algorithm
In this section, the framework of the GPPSO and its main components are discussed in detail.First, we present the mixed-variable encoding strategy, which is used to encode different types of CNN hyperparameters in the same form.Subsequently,we explain the HSA model used to search CNN hyperparameters, which deals with the expensive computational cost problem.We also detail the novel AF,which ensures convergence rate and model performance.Finally, we present the complete algorithm for better understanding of the proposed GPPSO.
3.1 Mixed-variable encoding strategy
In GPPSO, each sampled individual represents a group of CNN hyperparameters, where each dimension of the individual corresponds to a CNN hyperparameter.Because the CNN hyperparameters have distinct meanings, each individual has its own specific types and constraints.For example, some hyperparameters should be set as integers with a large range, such as the number of Conv kernels,whereas some hyperparameters should be discrete,such as the size of Conv kernels.Most traditional optimization methods are aimed at a single type of variable, which is difficult when optimizing mixedvariable types.Therefore, it is important to design a mixed-variable encoding scheme for handling the mixed-variable problem.
Table 1 provides the CNN hyperparameter settings to be optimized in this study.In particular,the variables with many available choices or a large search range are encoded as continuous variables,whereas the variables with several fixed selections are encoded as discrete variables.Although the variables of Conv kernels and FC layer neurons are required to be integers, regarding them as continuous variables can be more flexible and efficient in the optimization process.The reason for processing integers as continuous variables is that the search space for the numbers of kernels and neurons is large and does not have a prior known upper bound(e.g.,[1,+∞)),which is inefficient and complex to encode them as finite integers.As for the discrete variables with only a few choices, we encode these discrete variables in a continuous way.The advantages of encoding discrete variables in this way are as follows: first,the size of Conv kernels, the types of AFs, and the types of pooling layers have only three or four available results.These results correspond to a small search space (e.g.,{0,1,2,3}), which is feasible for continuous encoding.Second, encoding continuous variables and discrete variables in the same way is convenient and efficient, which is conductive to the GPPSO algorithm.
Based on the above analysis,the mixed-variable encoding strategy is given as follows: in detail,Xof every particle is a vector with dimensionD; each dimension represents a CNN hyperparameter.As a result, each vectorXrepresents an architecture of the candidate CNN structure.Because each dimension has a different meaning and the range of values in each dimension is different, the following strategy is designed for encoding: first, for the integer variable in continuous variables, the encoding strategy is shown in Eq.(9):
whereNkdenotes the number of kernels in the Conv layer,Xnkdenotes the search result of the number of kernels by the optimization method,and■·」denotes taking the largest integer that is no larger than the search result.Using this method, we translate the continuous variable in[1,+∞)to an integer variable.Because the initial learning rate and dropout rate are consecutive floating-point values in the search space, the GPPSO’s result can be used as the final result during search.For discrete variables, each of their available values corresponds to an integervalue, and the search range is set according to all the integer values that can be taken.Taking the example of discrete variable encoding for AF, the specific encoding strategy is shown in Eq.(10):

Table 1 Settings of mixed-variable encoding for CNN hyperparameters
where af denotes the final result of AF,Xafdenotes the GPPSO search result,and「·■denotes taking the smallest integer that is no less than the search result.
3.2 HSA model
After encoding the CNN hyperparameters using a mixed-variable encoding scheme,the GPPSO algorithm starts to search for the optimal hyperparameter combinations by the HSA model.As shown in Fig.4, the search process is divided into two parts,master and slave.In the first part, the candidate model is evaluated by constructing a GP model at multiple levels.In the second part,the target model of the next exploration is generated according to the previous search results through the PSO algorithm.
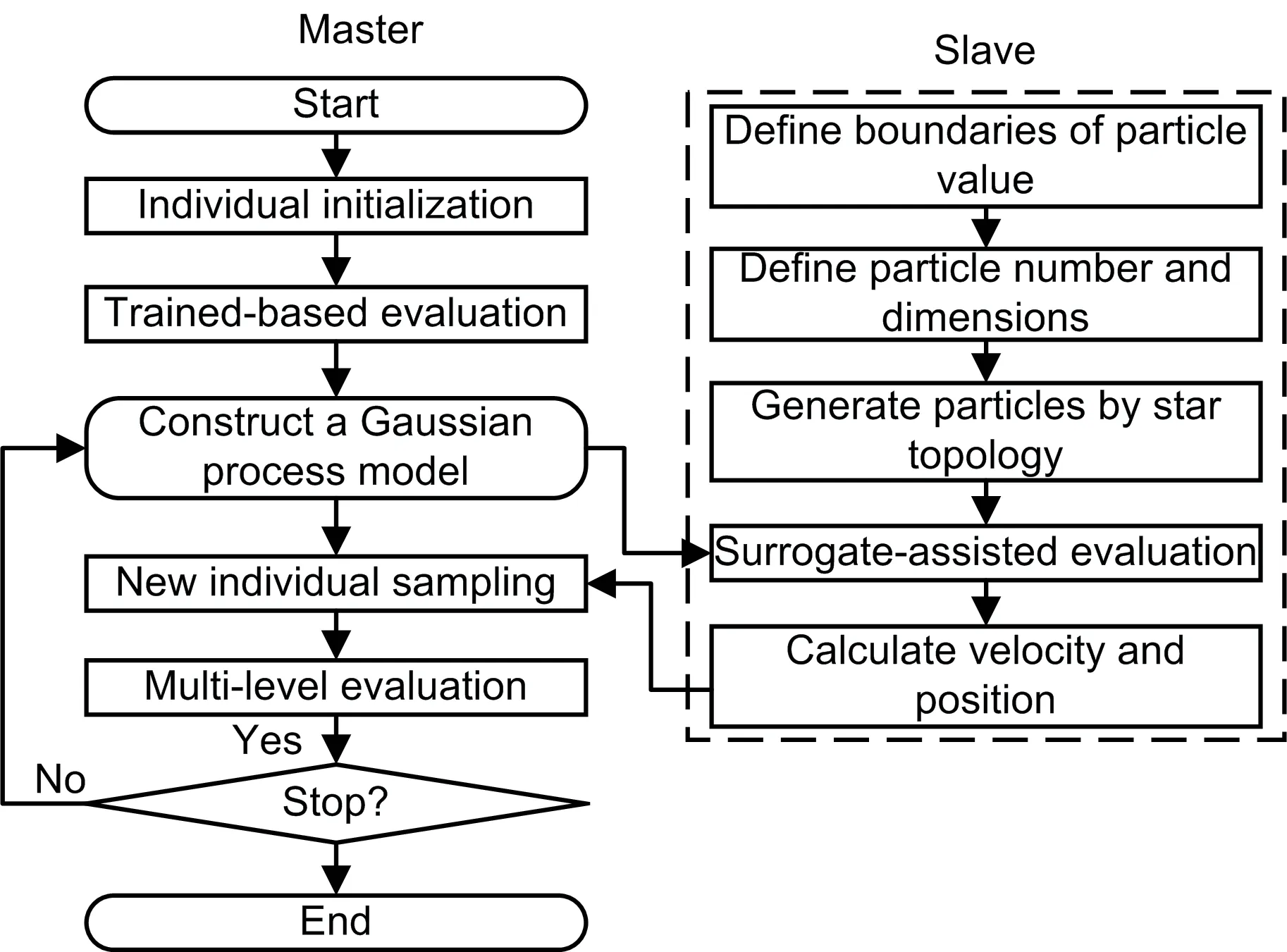
Fig.4 General flowchart of the hybrid surrogateassisted model
3.2.1 Multi-level evaluation strategy based on GP
Because of the large size of CNN models and the large amount of training data, evaluating their fitness(i.e.,classification loss or accuracy)is computationally expensive.Furthermore, even if there are enough computational resources and time to train the model until the accuracy converges, the optimal model obtained cannot guarantee, still having the best performance on the test set due to the difference between the validation data and test data.Therefore,unlike traditional OA,which obtains convergence accuracy through a lot of training as a fitness value, GPPSO is more efficient in evaluating and comparing different CNN candidate structures using a multi-level evaluation strategy.
GPPSO improves the computational expensive problem from two perspectives.First,GPPSO trains candidate models with few epochs during the search process to distinguish performance of different individuals.Second, a multi-level evaluation strategy based on GP is designed for the computational expensive problem in the search process.Each candidate is preliminarily computed by the GP model,and then some individuals with better evaluation results are trained to construct a new GP model.In addition, to improve the robustness of the algorithm, it is necessary to ensure that at least one individual of the group is evaluated by training.The pseudocode of the multi-level evaluation strategy based on the GP is given in Algorithm 1.
3.2.2 Individual generation strategy based on PSO
During the search process of GPPSO, it is necessary to evaluate individuals many times by the multi-level evaluation strategy and cause individuals to evolve to obtain the best outcome.Every time the multi-level evaluation strategy in Algorithm 1 is executed,an individual generation strategy is required to produce new candidates for the next subsequent generation.Traditional OA based on GP, such as the BO algorithm,defines an acquisition function to evaluate whether a sample can provide benefits for the GP model, and then determines whether it is a new individual to be explored.However,traditional acquisition functions generate new individuals based on existing individuals, which results in an incomplete search process, insufficient adaptability, and a limited exploration area.
Because the exploration performance of the above acquisition function may be not enough to generate new individuals accurately, an individual generation strategy based on PSO is proposed to increase performance in generating candidate individuals.The method is inspired by the PSO algorithm,candidate structures are treated as a group of particles, their initial value is treated as the position,and their velocity is calculated according to the GP model.After iterating through the PSO, the optimal offspring obtained is the new individual to be evaluated in Algorithm 1.The specific pseudocode is shown in Algorithm 2.

Algorithm 1 Multi-level evaluation strategy Input: Dataset of training CNNs, Dtrain;dataset of evaluating CNNs, Deval;architecture constructed by individuals, Parch;fitness of individuals in the architecture, fitarch;set of individuals to be evaluated, P;number of initial individuals, NI;number of all individuals, NA;number of training epochs, T Output: Set of individuals evaluated, Peval;the fitness set of individuals evaluated, fiteval 1: begin/* construct the initial GP model */2: Initialize NI individuals;3: Obtain Parch and fitarch of the initial individuals by training;4: GPI ←build an initial GP model with Parch and fitarch;/* first level evaluation by the GP model */5: gfitness ←fitness of P predicted by GPI;6: afitness ←the average fitness of fitarch;7: Peval ←empty set;8: fiteval ←empty set;9: ri ←a random integer in {1,2,···,NA};/* second level evaluation by training */10: for each individual Pi in P do 11: if gfitness>afitness or ri==i then 12: Net ←build a candidate architecture according to the hyperparameters in Pi;13: Net ←train Net with T epochs on Dtrain;14: accuracy ←validate Net on Deval;15: fiteval ←fiteval ∪{accuracy};16: Peval ←Peval ∪Pi;17: GPI ←evolve GPI through fiteval and Peval;18: end if 19: end for 20: end
3.3 An improved AF

Algorithm 2 Individual generation strategy Input: The initial Gaussian process model, GPI;number of particles, N;fitness of individual i, fiti;dimension of particles, d;number of generations, n;number of iterations, T Output: The generated individual to be evaluated,Pnew 1: begin:/* initialize a group of particles with d dimensions corresponding to hyperparameters in CNNs */2: Initialize a set of N particles as P;3: for each particle Pi in P do 4: for each dimension d of Pi do 5: Randomly initialize the particle position xid within the given range;6: Randomly initialize the particle velocity vid within the given range;7: end for 8: end for/* search individuals for multi-level evaluation by PSO */9: for k =1 to T do 10: for each individual Pi in P do 11: fiti←calculated fitness by GPI in Algorithm 1;12: if the fitness value is larger than pbestid in history then 13: pbestid ←fiti;14: end if 15: gbestd ← the particle with the best fitness value;16: Calculate velocity vid through Eq.(7);17: Calculate position xid through Eq.(8);18: end for 19: end for 20: Pnew ←xid of the last n generations;21: end
AFs play an essential role in the CNN learning process by fitting complex functions.AFs can introduce nonlinearity into CNNs, and provide the entire model with the ability to solve complex problems.During the early development stage of neural networks, traditional AFs are mainly S-type saturation functions, such as Sigmoid and Tanh (Fig.5),which tend to cause vanishing gradients, resulting in training difficulties.Moreover, the derivative of these functions is complicated, and will cause computational expensive problems during the process of gradient back propagation in training.With the development of deep learning,Krizhevsky et al.(2017)proposed rectified linear units (ReLUs) (Fig.5) to solve the problem of vanishing gradients and speed up network training.However, the ReLU function has some limitations.Becausexvalue of the negative half-axis and its gradient value are both zero,neurons can lose the ability to transmit information during the training process.
In the automatic search for CNN hyperparameters, fast convergence, low computational cost, and high accuracy should be achieved in the network evaluation process.Traditional AFs are often unable to meet these requirements simultaneously.Therefore, a new AF has been designed as follows:
Ta-ReLU is a nonlinear and differentiable function with a sensitivity factorαthat controls the function’s negative semi-axis activity to the inputs.Whenα= 0, Ta-ReLU reduces to ReLU.The function is discontinuous atx= 0 and is sensitive to inputs on the positive semi-axes and to the inputs close to 0 on the negative semi-axes.When the input changes,the output also changes significantly.However,Ta-ReLU is insensitive to other inputs;that is,the output does not change in correspondence with the input or produces only a small change.Given these properties,Ta-ReLU meets the required conditions of an AF.A comparison between Ta-ReLU and traditional AFs is shown in Fig.5.
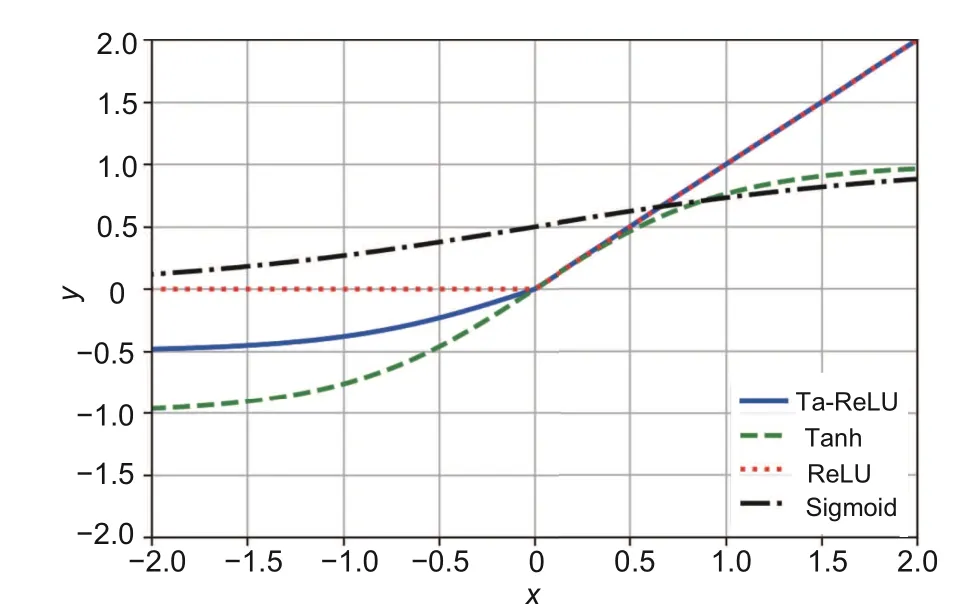
Fig.5 Comparison of different activation functions
Fig.5 shows that Ta-ReLU has several advantages compared to traditional AFs.First,it requires less computation and has a simpler derivative,making it more efficient and easier to implement.Additionally, Ta-ReLU has a larger gradient than ReLU at thex-negative half-axis near zero, ensuring that negative output values are not ignored in the network.This leads to higher search speeds during training and results in better performance in the trained model.These advantages will be further verified in Section 4.
3.4 Complete algorithm
The complete pseudocode of GPPSO is shown in Algorithm 3 and is detailed as follows:
Step 1: GPPSO initializes a set of individuals through a mixed-variable encoding scheme(Section 3.1)and evaluates these initial points (IPs)using training to determine their accuracy.Then,according to the accuracy, the best individuals and their fitness values will be evaluated and stored.

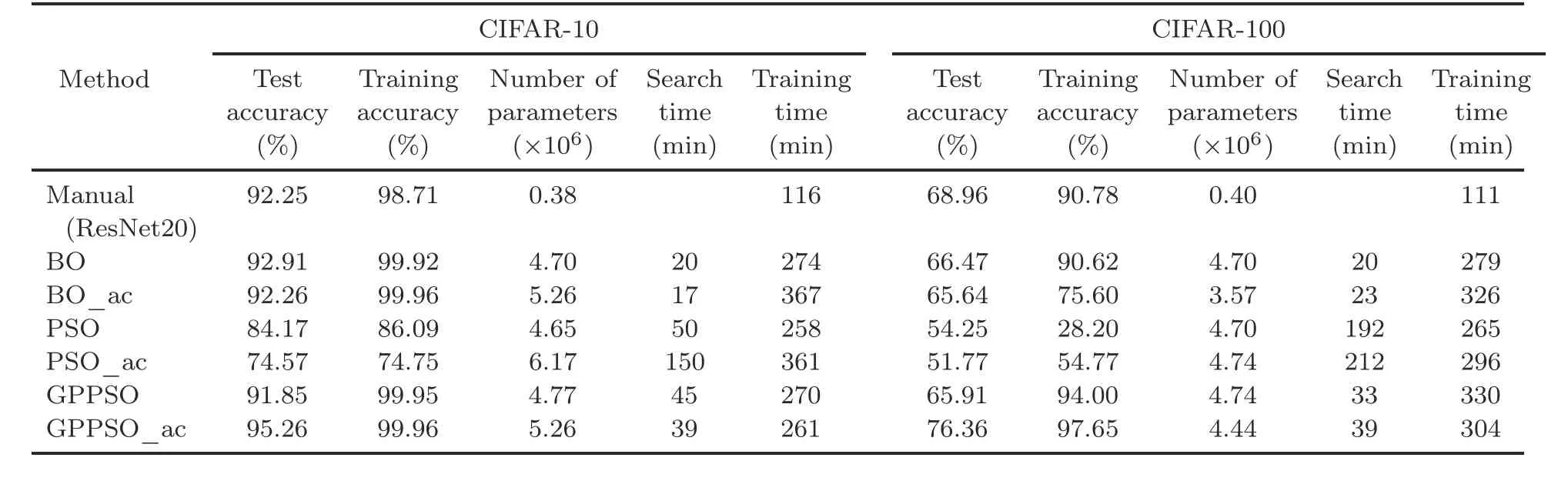
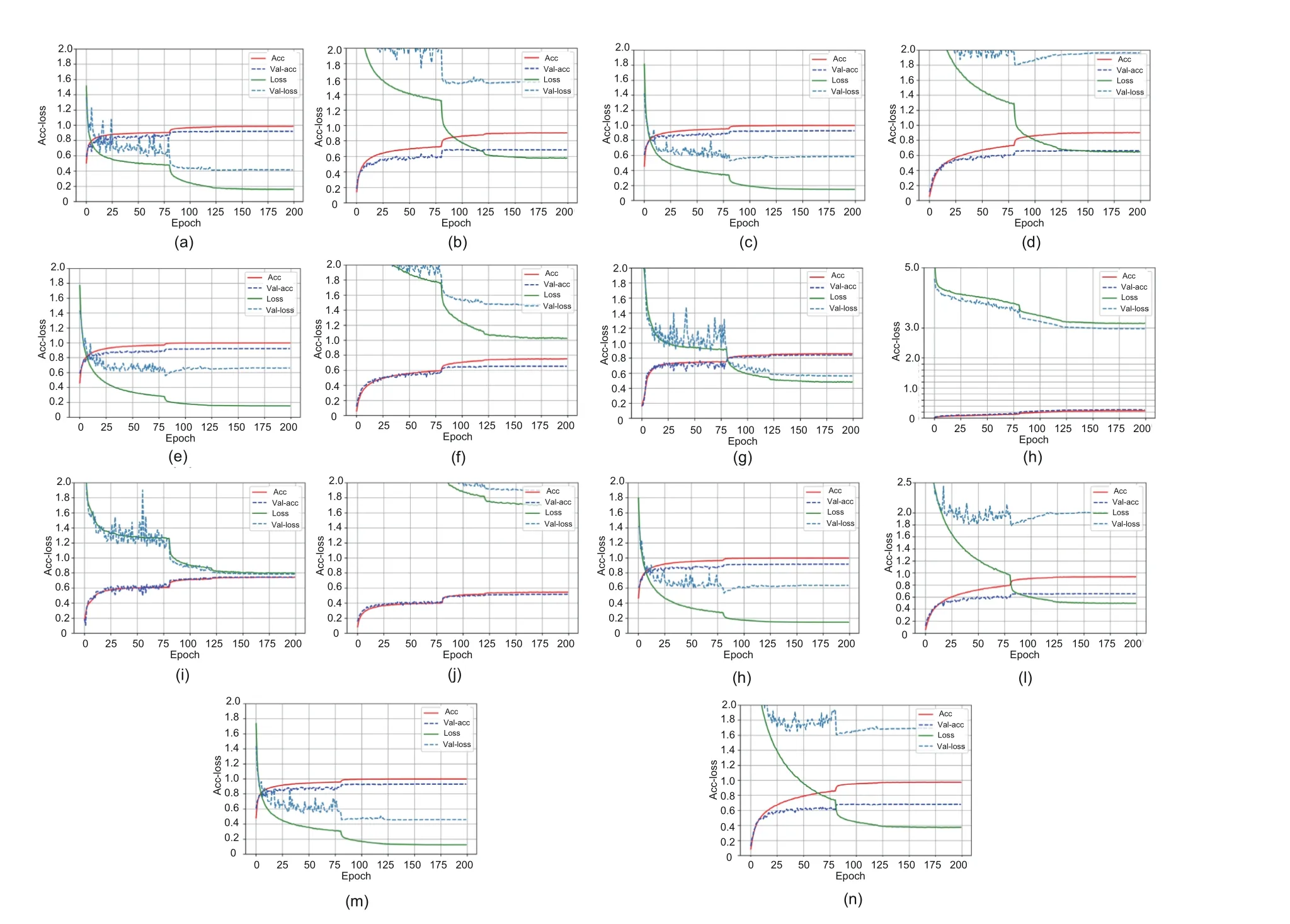
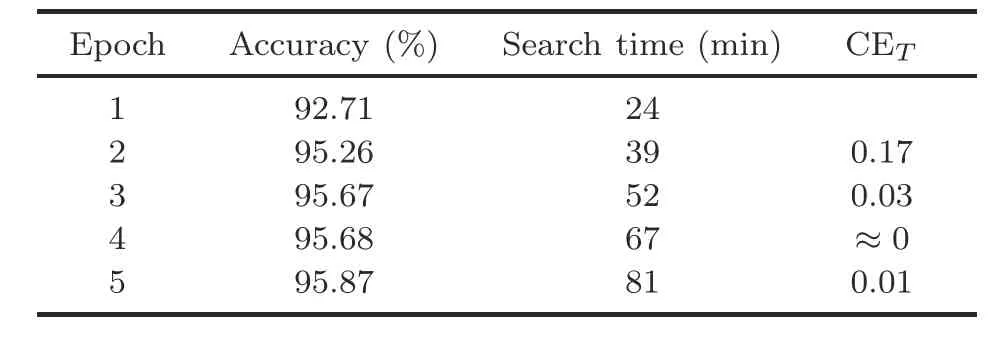
Algorithm 3 Complete algorithm Input: Input dataset, DI;number of initial individuals, NI;number of sampling individuals, NS;the initial Gaussian process model, GPI;the initialized continuous variables, cx;the initialized discrete variables, dx;number of iterations, T Output: The architecture searched by GPPSO, Net 1: begin:2: Dtrain, Dvalid ←split DI by 5:1;3: cx, dx←perform mixed-variable encoding strategy;4: P ←combine cx and dx;5: fitness ←∅;6: for each particle Pi in P do 7: Net ←build a CNN according to Pi;8: Net ←train Net with S epochs on Dtrain;9: accuracy ←test Net on Dvalid;10: fitness ←fitness ∪{accuracy};11: end for 12: Pbest,fitbest ← the best individual and fitness,respectively;13: Parch ←P, fitarch ←fitness;14: search_iteration ←0;15: while search_iteration Step 2: for the first loop, setting search_iteration to zero.According to the evaluated points in step 1, the initial GP model is constructed.It should be noted that the GP model is dynamically updated during the cycle, and the GP model will evolve each time based on the evaluation results of candidate points unless the iterations are reached.In the process of candidate point evaluations, a multi-level evaluation strategy(Algorithm 1)is adopted to solve the computational expensive problem and improve the search efficiency. Step 3: during the cycle, new candidate points need to be generated for evaluation through an individual generation strategy based on PSO(Algorithm 2).First, the boundaries, numbers, and dimensions of particles are set to generate particles through a star topology, and then the fitness of the particles is evaluated using the GP model.After several evolutionary iterations,the optimal particles are obtained for multiple evaluations. Step 4: if the stop iterations are not met, the algorithm goes back to step 2 and the procedure is repeated; otherwise, the CNN constructed by the corresponding optimal hyperparameters is trained on the entire dataset for the best performance and outputs the CNN model as the final output.It should be noted that the Ta-ReLU designed in Section 3.3 is used as the AF of the Conv layer in the GPPSO algorithm.This choice aims to accelerate the convergence and ensure the model performance. To verify the effectiveness and efficiency of the proposed GPPSO, a series of experiments were designed and conducted.First, the relevant settings of the experiments are introduced in Sections 4.1–4.3, including the datasets and evaluation metrics,the compared state-of-the-art methods, and the parameter settings of the proposed algorithm.Next,the proposed GPPSO is compared with advanced algorithms on the CIFAR datasets to investigate its theoretical effectiveness.Finally, a metal fracture(MF) diagnosis case in a real-world industrial scenario is presented to prove the feasibility of GPPSO in practical industrial applications. To evaluate the performance of the proposed GPPSO, three datasets were used for experimentation in this subsection: CIFAR-10, CIFAR-100,and the MF dataset.Two different CIFAR datasets(Fig.6) were used to verify the theoretical effectiveness of the proposed algorithm, because they provided varying difficulties for image classification tasks.Both CIFAR datasets contained 50 000 training images and 10 000 test images, where each image has 32×32 pixels and three channels.The MF dataset was used in the experiments to demonstrate the effectiveness of GPPSO in practical applications.The MF dataset consisted of 1500 scanning electron microscopy images of three MF categories, with the resolution of 512×512.The initial dataset was expanded from 1500 to 7500 by random angle rotation,proportional scaling,horizontal and vertical flipping,and a training-to-test set ratio of 4:1.Fig.7 shows the examples of the MF dataset. Fig.6 Examples of the CIFAR datasets Fig.7 Examples of the metal fracture dataset: (a)cleavage fracture; (b) intergranular fracture; (c) dimple fracture During the experiments,three aspects were considered to compare the algorithm’s strength: model performance, model size, and model training time.In terms of these aspects, three popular metrics were adopted: the classification accuracy on the test dataset,the number of parameters in the model,and the time consumed.It should be noted that the time required for training is different for each computer due to the different hardware configurations even with the same graphics processing unit(GPU).Therefore, GPU days were used only as a reference index of other methods; the training time in our experimental environment was used as a horizontal comparison index. To demonstrate the effectiveness of the proposed GPPSO,a series of state-of-the-art algorithms were used for comparison based on the evaluation metrics in Section 4.1.The compared algorithms can be divided into three categories: manually designed CNNs, non-OA-based methods, and OAbased methods. Specifically, the manually designed CNNs include the famous architectures maxout (Goodfellow et al., 2013), network in network (Lin et al., 2013),ALL-CNN(Springenberg et al.,2014),VGGNet(Simonyan and Zisserman,2014),highway network(Srivastava et al., 2015), FractalNet (Larsson et al.,2016), ResNet (He et al., 2016), and DenseNet(Huang et al., 2017), which have shown state-ofthe-art results in image classification tasks.For the non-OA-based methods, some representative algorithms are adopted,such as BO(Snoek et al.,2012),Auto-Keras(AK)(Jin et al.,2019),NAS (Zoph and Le, 2017),MetaQNN(Baker et al.,2017),EAS (Cai et al.,2018),and Block-QNN-S(Zhong et al.,2018).As for the OA-based algorithms, PSO, hierarchical evolution(Liu et al., 2017),large-scale evolution(Real et al., 2017), genetic CNN (Xie and Yuille,2017), CGP-CNN (Suganuma et al., 2017), CNNGA(Sun et al.,2020a),AE-CNN(Sun et al.,2020b),AE-CNN+E2EPP (Sun et al., 2020c),and SHEDACNN (Li JY et al., 2023) are selected to compare with GPPSO.Because of the better performance of OA-based methods in automatic search algorithms,these methods are ideal for comparison with GPPSO.Due to the expensive computational cost and different experiment environments, some final results of the literature were cited directly for comparison,which is also a convention in the deep learning study.In addition, to ensure the effectiveness of the comparisons, the classical algorithms in each category,such as ResNet50, BO algorithm, and PSO algorithm, were implemented in the experimental configuration of this study to make a direct comparison with various indicators of GPPSO. A 20-depth version of ResNet was used as the basic model of GPPSO in the experiments on the CIFAR datasets.There were 19 Conv layers and one pooling layer in ResNet20 for feature extraction,and one FC layer and a final softmax layer for image classification.According to the ResNet20 structure and mixed-variable encoding strategy (Section 3.1), the model was encoded using 22-dimensional continuous variables and 32-dimensional discrete variables.The specific setting is shown in Table 1. The GPPSO parameters were set as follows:first, considering the balance between the computational cost and model performance,the number of IPs selected to build the GP model was 20.Second,the minimum number of iterations was set to 30,after that the search will finish when a better CNN cannot be found in three generations.In addition, the candidate model obtained through the search process will be trained for two epochs as a preliminary evaluation of performance.As for the individual generation category,the parameters were configured according to the default values in PySwarms(Miranda,2018):c1= 0.5,c2= 0.3, andw= 0.9.Finally, for the CNN training category, the optimizer was set as Adam, and the initial learning rate was set to 1×10-3. In addition,data augmentation was applied before training using the conventional method through Keras.The experiments were conducted and evaluated using the Python programming language with the TensorFlow(Abadi et al.,2016)deep learning library on a 2.30 GHz Intel Core i7-12700H CPU and 16 GB memory NVIDIA RTX 3080Ti graphics card. The effectiveness of the GPPSO algorithm was evaluated using two comparisons, as shown in Tables 2 and 3.The first part represents the comparison between GPPSO and state-of-the-art algorithms.Then in the second part, a comparison between GPPSO and the basic algorithms (BO and PSO)is presented. As shown in Table 2, the GPPSO required 0.04 GPU days to achieve 95.26% classification accuracy with 5.26×106parameters on the CIFAR-10 dataset and to achieve 76.36% classification accuracy with 4.44× 106parameters on the CIFAR-100 dataset.Compared with state-of-the-art algorithms, GPPSO shows the great performance in both classification accuracy and search time.First,when compared with the manually designed models, GPPSO achieves at least 0.53% and at most5.03% classification accuracy improvement on the CIFAR-10 dataset.As for the CIFAR-100 dataset,GPPSO achieves at most 24.36%accuracy improvement over maxout, and just 3.15% lower than that of the 20-layer version of ResNet, proving that instead of trying deeper and more complex network models, optimizing the hyperparameters of existing well-performing CNN models using GPPSO can obtain outstanding results.As for the number of parameters, the model searched by GPPSO generally has fewer parameters than the directly connected networks such as VGGNet, but more than cross-layer connection models such as ResNet due to the concatenate and other operations.Second,compared with the non-OA-based methods,GPPSO still achieves better performance.On the CIFAR-10 dataset, GPPSO achieves better classification accuracy, and is better than BO, AK, MetaQNN, and NAS by 2.53%, 7.56%, 2.34%, and 1.35%, respectively.As for EAS and Block-QNN-S, GPPSO can achieve similar classification accuracy, but greatly reduces the search time.This means that GPPSO needs less time and computational cost to search for better CNN models.For example, for the non-OA-based methods, NAS needs 22 400 GPU days to find a good CNN model and EAS requires at least 10 GPU days, but GPPSO needs only 0.04 GPU days.On the CIFAR-100 dataset, the accuracy of GPPSO is a little worse than that of Block-QNNS, but still achieves good performance of 76.36%.GPPSO has more model parameters than the NAS and AK methods, but fewer than the other algorithms.Finally,compared with the OA-based methods, GPPSO still obtains competitive results.As shown in Table 2,for classification accuracy,GPPSO ranks the fifth among the 10 algorithms based on the CIFAR-10 dataset, with up to 13.18% higher accuracy than that of PSO and 1.57% lower accuracy than that of the first algorithm (CNN-GA).As for CIFAR-100, GPPSO achieves good performance and ranks the sixth among the eight algorithms, 40.76% better than that of the last and only 3.91%lower than the first.However,compared with CNN-GA, GPPSO cost only about 0.11% and 0.10% GPU days on CIFAR-10 and CIFAR-100, respectively.When compared with the SHEDA-CNN method,GPPSO not only reduces the search time by 93.10%and 95.88%,but also reduces the model size by 51.65% and 76.18%, on CIFAR-10 and CIFAR-100 datasets respectively.This means that GPPSO not only achieves good recognition performance,but also greatly reduces the search time and model size.These advantages provide strong feasibility for the practical applications of deep learning.The above comparison results show the effectiveness and effi-ciency of GPPSO. Table 2 Comparisons with the manually designed CNNs, non-OA-based methods, and OA-based methods on CIFAR-10 and CIFAR-100 datasets Table 3 presents a set of comparisons between GPPSO, ResNet20, BO algorithm, and the PSO algorithm to show the outstanding performance.It should be noted that all the results in Table 3 were generated in the experimental environment of this study, and algorithm_ac denotes that Ta-ReLU in Section 3.3 is in the search space.Because the experiments were carried out under the same hardware conditions, minute is used as the benchmark index for efficiency comparisons instead of GPU days.It can be seen in Table 3 that GPPSO_ac achieves the best test accuracy on CIFAR-10 and CIFAR-100,where it is 3.26%and 10.73%better than that of the basic model ResNet20 on CIFAR-10 and CIFAR-100,respectively.By using the automatic search method for manually designed CNN ResNet20, the accuracy will be improved by the BO algorithm and reduced by the PSO algorithm, whose test accuracy is lower than that of GPPSO.The number of parameters of the manually designed CNN is significantly smaller compared to those of the automatically searched models.Furthermore, the numbers of parameters in the automatically searched CNNs are in a similar order of magnitude (106).We think that this is due to the concatenate layer and other structures in the automatic search networks.As for the search time, the BO algorithm needs least 17 min to search CNNs, GPPSO takes longer time than BO, 42 min on average, and PSO takes the longest time at an average of 100 min on CIFAR-10 and 202 min on CIFAR-100.After searching for the CNNs, we train them for 200 epochs to obtain the final models.The accuracy-loss curves of training are shown in Fig.8.It can be seen that the convergence speed of the model on the CIFAR-100 dataset is lower than that on CIFAR-10,and the error value is higher than that of CFIAR-10,which indicates that the 20-layer basic model has limited capability for large-scale output categories.For the model with Ta-ReLU function,the convergence rate is higher in the first 20 epochs(e.g.,Figs.8m and 8k),and GPPSO_ac has the best recognition accuracy on CIFAR-10 and CIFAR-100,which proves the effectiveness of the designed AF. In conclusion,the comparisons with the basic algorithms of GPPSO and state-of-the-art algorithms prove the effectiveness and efficiency of GPPSO. In the GPPSO algorithm,the initial GP model will be constructed from a set of individuals, so the number of individuals may affect the GPPSO performance.To verify the influence of the number of IPs,GPPSO is compared with variants using different numbers of IPs on CIFAR-10.During the experiments, the range of the number of IPs was set from 10 to 50,and the sampling interval was set as 10;the experimental results are shown in Table 4.It can be seen that with different numbers of IPs, the classification accuracy of all searched models is>92.50%,and the search time increased almost linearly, with an additional 5 min required for each sampling interval increase.Furthermore,the classification accuracy initially increased and then decreased with an increase in the number of IPs,with peak performance achieved when the number of IPs was 20.This indicates that the model searched by GPPSO does not achieve higher performance with an increased number of IPs.We think the reason is that the random IPs cannot precisely describe the trends of Gaussian regression model, and the points obtained by acquisition function in the search process are more meaningful.In conclusion, the number of IPs can influence the search effectiveness of GPPSO,but the GPPSO is not that sensitive with the increase of the number of IPs, and the performance is not always improved with an increased number of IPs. Another important parameter in GPPSO is the particle number (PN) in PSO.To investigate the influence of PN, a set of comparisons are given in Table 5.It can be seen that GPPSO is compared with its variants using PNs from 10 to 100; with the PNs increase,the classification accuracy exhibits similarity, when PN=30, 70, and 100, the accuracy can achieve>93%, and when PN=50, the performance of GPPSO is at its best (>95%).That is because GPPSO is not sensitive to the PN.In addition, with an increase in the PN, the GPPSO’s search time increases as well.Therefore,consideringthe performance and the computation costs,PN=50 is suitable and is recommended for GPPSO. Table 3 Comparisons with the basic algorithms of GPPSO on CIFAR-10 and CIFAR-100 datasets Fig.8 Accuracy-loss curves of training and validation on the CIFAR-10 and CIFAR-100 datasets: (a)ResNet20-10; (b) ResNet20-100; (c) BO-10; (d) BO-100; (e) BO-ac-10; (f) BO-ac-100; (g) PSO-10; (h) PSO-100; (i)PSO-ac-10; (j) PSO-ac-100; (k) GPPSO-10; (l) GPPSO-100; (m) GPPSO-ac-10; (n) GPPSO-ac-100 In the GPPSO process, after evaluating by the surrogate-assisted model, qualified models will be evaluated based on training.Hence, to reduce the time consumption and the computational cost, only epochTwill be selected for training,which will be a key issue for the effectiveness of the GPPSO.Therefore, an experiment between different epochTvalues was carried out to study the influence on performance.Considering the hardware performance of the experiments and the time complexity of thepractical applications, GPPSO was used to search for optimal CNNs by training epochTfrom 1 to 5 in the experiments.Table 6 shows the experimental results of different epochTvalues on CIFAR-10.To intuitively compare the impact of epochTon model performance, as shown in Eq.(12), a comparison method is designed to measure it: Table 4 Comparion with different numbers of initial points on CIFAR-10 Table 5 Comparison with different particle numbers(PNs) on CIFAR-10 where CETdenotes the ratio between the accuracy(acc) difference and the search time difference.It can be seen that when the epochs increase from 1 to 2, the classification accuracy is improved by 2.75%,and CETis 0.17 whenT=2.Then, as the number of epochs changes from 2 to 5, the value of CETchanges from 0.03 to 0.01,and approximately equals 0 whenT=4.This means that continuing to increase the epochs will not improve the performance obviously and will consume a lot of computational resources.In conclusion, the epochT=2 of training in the search process will result in the maximum GPPSO efficiency. Table 6 Comparison with different epochs on CIFAR-10 To prove the effectiveness of GPPSO in realworld problems, an application concerning MF diagnosis in industrial scenarios is presented in this subsection.Metal materials are essential in modern industrial fields such as aerospace, transportation,and metallurgical manufacturing.In a complex environment, metal materials in service cause failure accidents such as fracture, corrosion, and fatigue,which cause heavy economic losses and casualties.Therefore,to achieve accurate MF recognition automatically and efficiently, AI methods such as CNNs will be used, which are suitable for testing the performance of GPPSO. In the experiments, a deep learning metal fracture classification(DMFC)model is designed to recognize MFs.The model structure is shown in Fig.9. Fig.9 DMFC model structure (FC: fully connected;BN: batch normalization) The Conv kernels in the DMFC model are all 3×3, and three pooling layers are constructed using one max pooling layer and two average pooling layers.A flatten layer is added to reduce the dimension of the output feature maps produced by the last Conv layer.This serves as a transition between the Conv layer and the FC layer.The first FC layer has 128 neurons, followed by a batch normalization(BN) layer and a dropout layer.The output layer has three neurons, corresponding to three types of MFs.DMFC is the basic model of MF recognition task.The GPPSO algorithm searches the Conv kernel size,Conv kernel number,pooling layer type,AF type, and other hyperparameters in the DFMC to obtain the GPPSO-DMFC. To test the effectiveness, comparisons among VGG, ResNet, DenseNet, DMFC, and GPPSODMFC are given in Table 7.The effectiveness and efficiency of the algorithms are measured by accuracy and training time,respectively.As shown in Table 7,the proposed DMFC model achieved an accuracy of 94.94% and a training time of 11 s/epoch.When using state-of-the-art methods,the recognition accuracy of MF is significantly improved.However, the training time is increased.For example, DenseNet achieved an accuracy of 98.03%, but required training time of 93 s/epoch.After using the GPPSO algorithm to search hyperparameters for the DMFC model, the result achieved the highest accuracy of 98.16% and the shortest training time of 9 s/epoch,indicating the effectiveness and efficiency of GPPSO.Therefore, this application shows that the GPPSO has potential for solving real-world tasks. Table 7 Results of the metal fracture diagnosis In this paper, a novel method, GPPSO, was proposed for efficient optimization of CNN hyperparameters.First,the GPPSO encoded different types of hyperparameters in CNNs using a mixed-variable encoding strategy to deal with the mixed-variable problem.Then, the HSA model based on the GP and PSO was designed to save computational costs.Finally, a novel AF, Ta-ReLU, was suggested to improve the model performance and ensure convergence rate.Experiments on two benchmark datasets have proven the efficiency of GPPSO.Furthermore, a series of ablation experiments have been used to investigate the parameter sensitivity.We also presented a case study of industrial scenarios to demonstrate the effectiveness of GPPSO in real-world tasks.For further work,we plan to(1)search for the CNN hyperparameters and architectures jointly and (2) design a more efficient OA for obtaining CNNs to handle engineering problems with practical applications. Contributors Han YAN designed the research and performed the experiments.Han YAN and Chongquan ZHONG implemented the software and drafted the paper.Yuhu WU, Liyong ZHANG, and Wei LU revised and finalized the paper. Compliance with ethics guidelines Han YAN, Chongquan ZHONG, Yuhu WU, Liyong ZHANG, and Wei LU declare that they have no conflict of interest. Data availability Due to the nature of this research, all authors of this paper did not agree for their data to be shared publicly, so supporting data are not available.4 Experimental results
4.1 Datasets and metrics


4.2 Compared methods
4.3 Algorithm settings
4.4 Comparisons with state-of-the-art methods

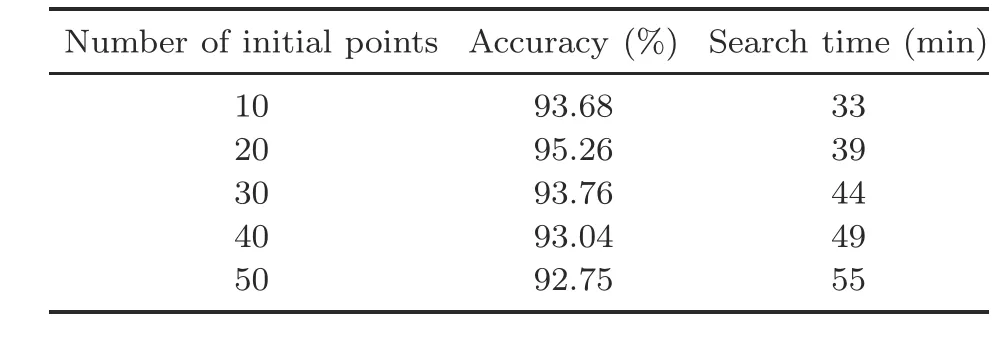
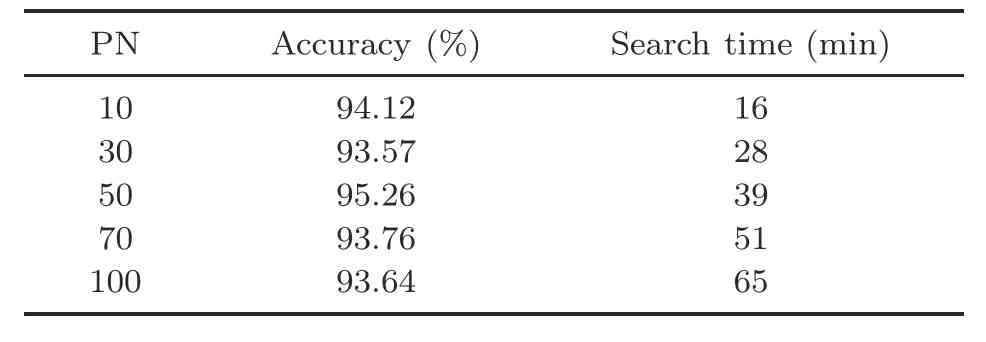
4.5 Ablation experiments
4.6 Application on MF diagnosis
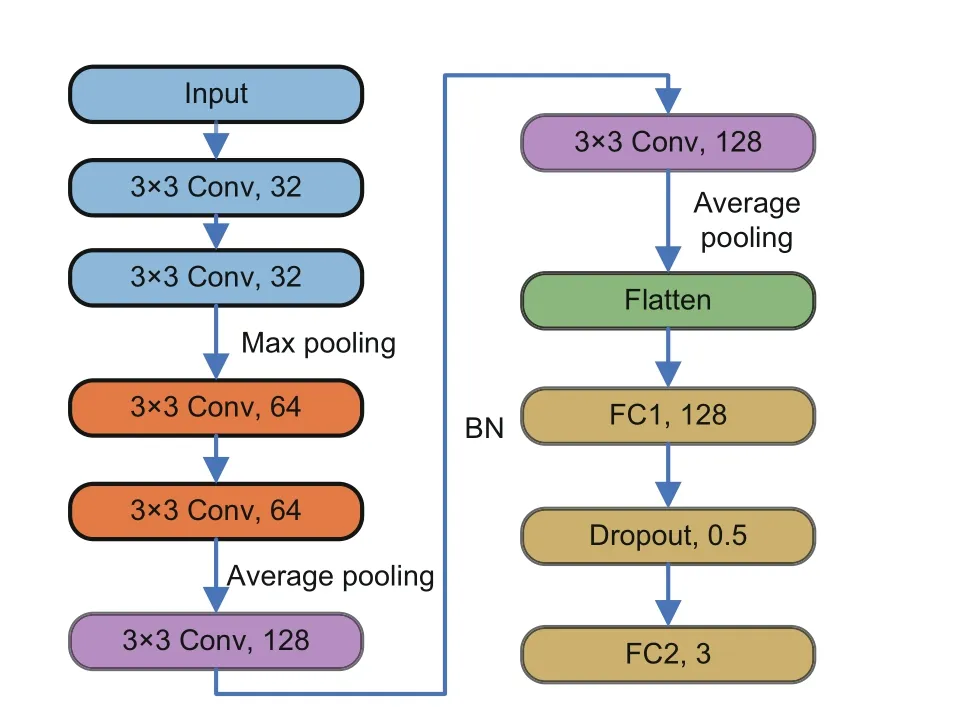
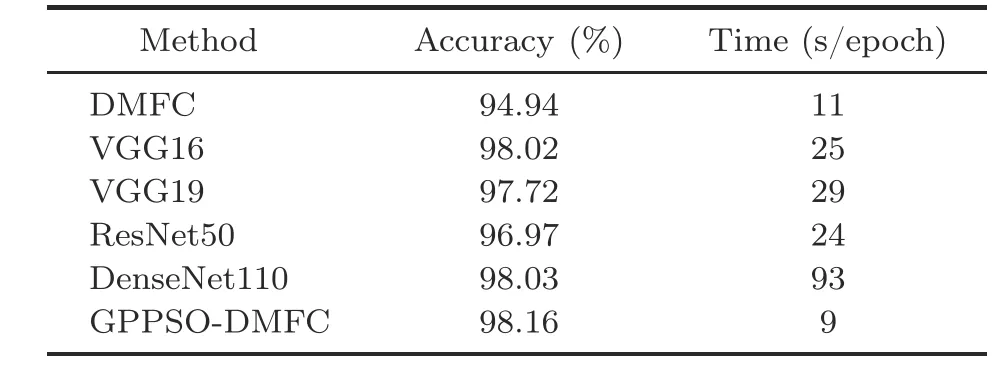
5 Conclusions
 Frontiers of Information Technology & Electronic Engineering2023年11期
Frontiers of Information Technology & Electronic Engineering2023年11期
- Frontiers of Information Technology & Electronic Engineering的其它文章
- Magnetically driven microrobots moving in a flow:a review*#
- Embedding expert demonstrations into clustering buffer for effective deep reinforcement learning*
- A high-isolation coupled-fed building block for metal-rimmed 5G smartphones*
- Dynamic parameterized learning for unsupervised domain adaptation*
- High-emitter identification for heavy-duty vehicles by temporal optimization LSTM and an adaptive dynamic threshold*#
- Hybrid-driven Gaussian process online learning for highly maneuvering multi-target tracking*
