启迪 渗透 深化
白凌晓 李娟
人教版小学数学教材中,优化思想无处不在。教师可以引导学生在计算方法多样化、解题方法多样化中体会优化思想,在解决有关最省钱、最省时等实际问题中感悟优化策略。如何采取循序渐进、行之有效的教学策略,让学生感受和体验运用优化思想解决问题的有效性,体会数学与生活的密切联系呢?笔者依托人教版数学教材,从三个方面谈谈培养学生优化思想的教学策略。
一、积微成著奠根基,启迪优化思想
优化思想贯穿整个小学阶段,教师要整体把握教材,在教学的方方面面启迪学生,让优化思想的种子在学生心中生根发芽,逐步取得积微成著的教学效果,为学生后续的学习奠基。
除了教材中的“优化”专题,第一学段的数学学习内容中就有优化思想的体现。如教学人教版数学一年级上册“20以内的加法”时,教师可以引导学生对比“凑十法”和“接着数”两种计算方法,体验“凑十法”的便捷性。这是对“凑零为整”优化思想的启蒙,可以为学生学习运算定律奠定基础。又如人教版数学二年级上册《乘法的初步认识》,在解决“玩过山车的一共有多少人?”时,学生通过列加法算式“2+2+2+2+2+2+2=14”感觉到书写的麻烦。教师乘机引导:“如果这辆过山车再长一些,需要10个2、20个2相加,你有什么感受呢?你有什么需要吗?”如此,教师引出乘法算式“7×2=14”,并通过两个算式的对比,使学生感知用乘法算式表示的简洁性与优越性,初步体会数学表达的优化。
二、追本溯源明定位,滲透优化思想
教师不能把数学思想当成一般的知识来传授、训练,而要牢牢把握思想方法渗透的目标定位,引导学生在自主探究、对比交流中感悟优化思想。
从数学广角承担的目标和学生学习数学的价值等方面考虑,人教版数学四年级上册《烙饼问题》的教学应定位于体验优化思想,但部分教师教学时往往侧重得出结果——烙饼所需最少时间的公式,在引导学生对烙2张饼、3张饼、4张饼进行简单操作后,便揭示“总面数÷每次烙的面数×每次烙的时间=至少需要的时间”,让学生借助公式计算烙7张饼、8张饼等需要的最少时间。这样教学,学生可能难以深刻领悟其中的优化思想,只是套用公式计算,一旦接触到一张锅里不是只放两张饼的题目,就无从下手了。
如何改进呢?教师首先要找准教学的起点和关键点;其次要落实操作,让学生的探究有抓手;最后要给学生充足的交流和讨论空间,让学生在对比中权衡多种方案,在体验中建构优化模型。具体地讲,烙2张饼是教学起点,烙3张饼是教学关键点,教师要在学生自主探究3张饼的烙法后,再组织学生讨论5张饼、6张饼、7张饼的烙法,引导学生发现烙单数张饼的最后3张时尤为重要。这样教学,学生才能通过多种方法的对比、权衡,得出“锅不空着”最省时也是“烙饼”的最优方案。
优化思想研究的是一个“序”的策略问题。在合理的前提下,改变做事的“序”,就会得到不同的结果,有时可以达到省时的效果。由“烙饼问题”推及其他内容,我们可以发现数学思想渗透的共性:让学生经历和体验知识的形成过程,理解知识及其背后的原理。
三、探路寻径理思路,深化优化思想
教师要引导学生理清建构多种解决问题方案的思维路径,并在多种方案中找出最优方案,进而体会优化思想对解决问题的效用,形成优化意识。
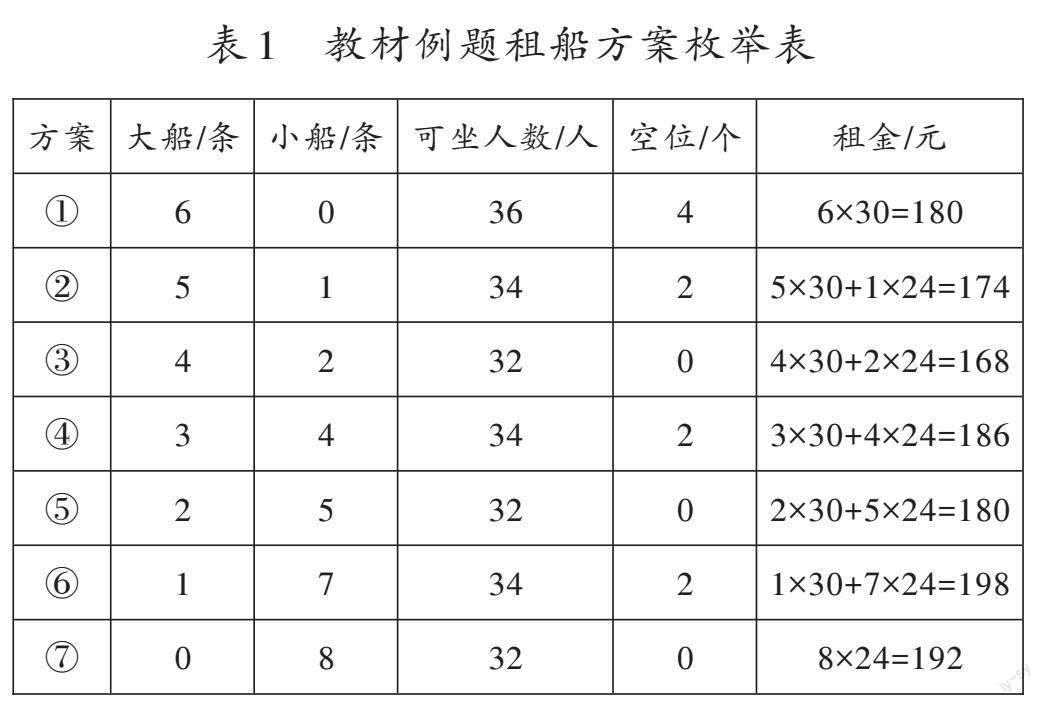
以人教版数学四年级下册“租船问题”为例,教材情境图中呈现了总人数(32人)、两种船的单价(小船24元、大船30元)、两种船的限乘人数(大船限乘6人、小船限乘4人)等信息。如何将这些数学信息关联起来,解决“怎样租船最省钱”的问题呢?教师通常引导学生先从“性价比”考虑,再从“无空位”考虑,快速得出“租4条大船和2条小船最省钱”的结论。这样教学会让学生对优化思想的体验浅尝辄止。要想深化学生的优化思想,教师就要重点引导学生经历在多种解决问题方案中找到最优方案的过程,分析这种方案最优的原因。教师可以采取“对比—思辨—归纳—提升”的路径来教学。
我们不妨先从“笨”方法——列表法入手(如表1)。通过对比,学生很容易发现表1中方案3最省钱。
接着,教师引导学生思考:为什么不是高性价比的大船租得越多越省钱?无空位的方案有三个,为什么方案③最省钱?怎样才能找到最优方案?然后,教师引导学生发现:方案①和方案②虽然大船数量多,但是有空位,有浪费;无空位的三个方案中,方案③的大船数量最多,所以最省钱。可见,最优方案不仅与“性价比”有关,还与“空位数”有关。
难道只要满足“尽可能租大船、没有空位”这两个条件,就一定最省钱吗?教师可以设计下面的练习,引导学生继续思考、辨析。
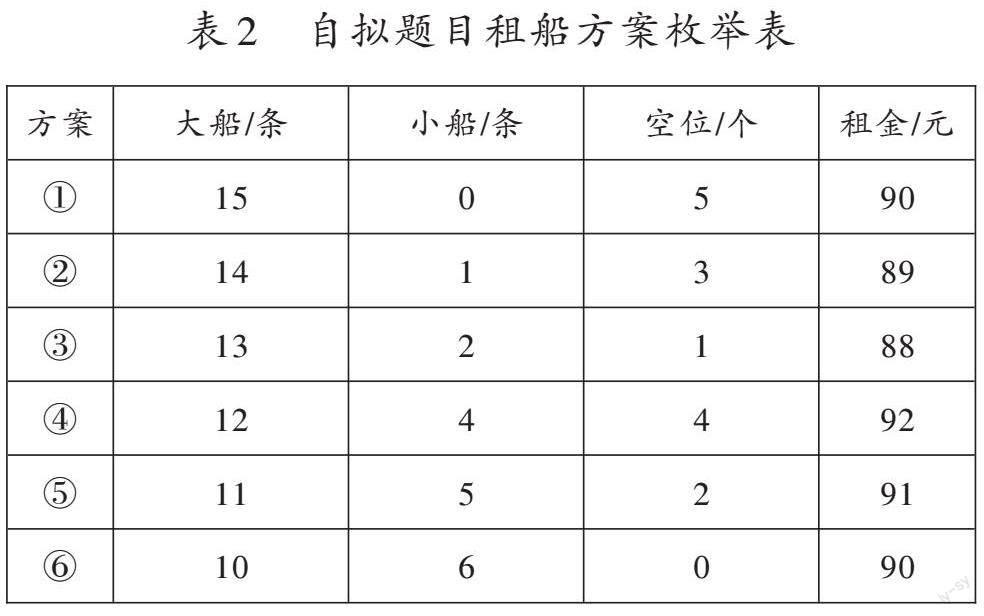
100人坐船,租1条大船需要6元,可乘坐7人;租1条小船需要5元,可乘坐5人。怎样租最省钱?
学生探究后形成三个方案:一是空位数为0的情况下,要租10条大船和6条小船,共需90元;二是全租大船的情况下,需要15条大船,共需90元;三是“余数坐小船”的情况下,要租14条大船,余下的人再租1条小船,共需89元。
最优解就是89元吗?我们继续列表(如表2)。
观察表2可知,最优解实际上是88元,即方案③最优,不属于前述任何一种情况。这是因为表2中方案③的大船数量比方案⑥多,空位数比方案①、方案②少,所以从“性价比”和“空位数”综合考虑,方案③最占优势。
教学至此,教师要引导学生深入思考:到底要列举出哪几种方案,才一定能找到最省钱的方案呢?通过观察表1,我们可以发现:空位数相同,大船租的越多越省钱。因此,表1中的三种无空位的租船方案中,方案③最省钱,三种有两个空位的租船方案中,方案②最省钱,我们只要比较方案①、方案②和方案③就能找出最省钱的方案。通过观察表2,我们可以发现:空位数越少,大船租得越多越省钱。因此,表2中的方案④、方案⑤和方案③比较,方案③更省钱。最终,我们只要比较表2中的方案①②③⑥就能找出最省钱的方案。通过以上分析,我们可以总结出必须列举的三种租船方案:一是全租大船,二是余数租小船,三是退大船租小船(空位较少、大船较多)。基于这三种情况展开比较、调适,我们就能找出最省钱的租船方案。
(作者单位:白凌晓,襄阳市教育科学研究院;李娟,枣阳市教学研究室)
责任编辑 刘佳
——《烙饼问题》教学实录与思考

