弱化解决数学问题能力差异的教学策略

彭其丽

基于第一学段的学习，三年级学生积累了一定的方法和经验，他们在解决问题时会采取不同的策略，思维发展呈現出较大差异。这些差异在各个知识模块的学习中均有体现，如在解决里程表类、年月日类、时间推算类等作答思路多样化的问题时，学生分析数量关系、寻找解题策略的能力出现两极分化的现象客观存在。

学生解决数学问题的能力两极分化的原因，笔者认为主要有以下两点。一是学生建模思维的发展程度不同。解决问题时，建模思维能力强的学生能够通过画图法、替代法、比较法等分析数量关系，建模思维能力弱的学生则无处下手，甚至胡乱列式计算。二是新课程背景下，数学问题的呈现往往依托真实而又相对复杂的实际背景，如推算时间问题、买票问题、车船安排问题等。学生理解这样的问题需要生活经验的支撑，有经验的学生知道题目中暗含的规则，而没有经验的学生可能无法准确理解题目的意思。

如何尽可能地弱化学生解决数学问题的能力差异？笔者在教学中主要采取以下策略。

一是为基础薄弱的学生查漏补缺。如部分学生在解决问题时不顾数量之间的关系，看到“多”就加，看到“少”就减。笔者教学这类问题（如“淘气有18元钱，比笑笑多5元钱，求笑笑有多少元钱”）时，先引导学生借助数线图表示两个量的关系，再引导学生反复用语言描述数量关系（淘气比笑笑多5元，笑笑比淘气少5元），深入理解题目中“多”与“少”的真正含义。

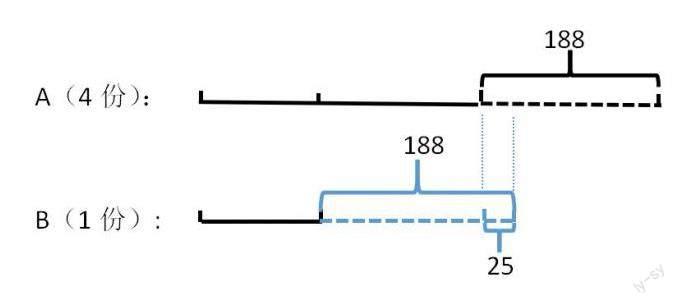
二是引导学生整理信息，发展建模思维。笔者在课堂教学中做好示范，引导学生用数线图、条形图等记录信息，分析信息，养成建构简单模型的解题习惯，积累建模的经验和方法。如常见的“差倍问题”：A是B的4倍，从A中拿出188给B后，A比B少25，求A、B各是多少？三年级学生没有学习方程，通过画数线图可以直观呈现数量之间的关系（如下图），进而用“（188×2-25）÷3”求出B，再用“B×4”求出A。

三是将数学问题生活化，让学生在实践中感悟知识。例如，学习“长方形的周长”时，如下两类题目学生常常出错。①一根长12分米的铁丝围成了一个长方形，当把这根铁丝围成一个正方形时，求正方形的周长。②周长为36厘米的长方形，它的长和宽分别可以是多少？对于问题①，笔者让学生实际操作，用一根绳子围一围，学生发现12分米的铁丝围成的长方形的周长就是12分米，改成正方形，其周长仍然是12分米。对于问题②，笔者让学生将一根绳子围成一个长方形，测量其长和宽（取整厘米数），讨论这根绳子可以围成几种不同的长方形。学生探究后发现规律，并推知：周长为36厘米的长方形，其长和宽的和是18厘米，把18分成一大一小两个数，大的数就是长，小的数就是宽，有几种分法就有几种长方形。

此外，教师要注重知识之间的关联，处理好教学衔接问题。数学知识具有结构性，对同一个知识模块，不同学段的学生要达到的目标不同。相关联的知识，教师应该教到什么程度？学生要掌握到什么程度？如何与前面所学内容建立联系？如何为后续学习做铺垫？这些问题需要教师依据课程标准要求，细化单元、课时目标，设计具体的学习活动，帮助学生以整体视角理解一个个知识点，形成知识结构。

（作者单位：潜江市田家炳实验小学）

责任编辑  刘佳