一种气体定律演示方法的设计及应用*

张泓筠 欧满琳 孟 波

(凯里学院大数据工程学院 贵州 凯里 556011)

1 基于气体状态变化规律实验教学分析

实际气体在压强不太大(和大气压相比)温度不太低(和室温相比)条件下,其性质可近似为理想气体.

教学用的某些气体定律演示器或结构复杂,或参数测定不透明、不直观,或参数调控不方便[1-3];有些会产生比较大的误差[4].相关实验存在的弊端主要表现在漏气、摩擦过大、状态量的变化太小不直观、使用水银等,为此产生了系列改进方法[5-11].我们认为,实验教学在演示原理准确、生动、直观前提下,应尽可能简化结构及步骤,突出实验现象.麦克斯韦也曾有更为精辟的论述,教育仪器的教育价值往往与仪器的复杂程度成反比,在能够直观展示物理原理、方便理解情况下,教学用自制的仪器进行研究学习比现成的仪器、仔细调整好的仪器要学到更多的东西.因而教学演示需要简化装置结构、简化测试过程,据此我们设计了一套简易方法可直观演示气体等温变化、等容变化、等压变化规律,甚至可验证克拉珀龙方程.在一定范围内可任意获取气体的状态参数,能做到实时性、动态性,具有放大现象变化效果.

2 教学设计

2.1 设计依据

(1)浮力是接触力,弹性力,气球静止于水下不同深度的地方,压强不同,受水的压力亦不同.在给定的容器-水-浮体系统,气球随着深度增加,受水的压力增大,体积变小,所受浮力减少,水面下降.

(2)调节气球在水中的深度可以控制球内气体的压强和体积[12];水浴加热可以改变气球的温度、体积和压强,因而本方法中,深度和温度的控制可随意改变气体的状态,体积量管可使体积变化现象更直观.

2.2 器材和装置图

2.2.1 器材

500 mL量筒(玻璃或塑料制,直径φ=50 mm),250 mL量筒,100 mL量筒,12号橡胶塞(上、下直径分别为62 mm, 51 mm),玻璃管2根(5 mm×7 mm,长度分别为200～300 mm,大于1000 mm),彩色小气球若干,钩码,细线,酒精温度计(量程0～60 ℃,用透明胶粘于筒内壁),充气装置[三通管或T形管、塑料注射器(100 mL或60 mL)、U型管、钩形管(长度大于1 m)],圆筒形水槽(直径φ=10～15 cm,高于盛水量筒2 cm,用于水浴恒温加热),乳胶管(5 mm×7 mm),长直滴管,米尺,铁架台2个,酒精喷灯,草木灰.

2.2.2 装置图

装置图如图1所示.

2.2.3 简易充气测压装置制作及使用

制作方法:

(1)按图1(a)所示装置将T形管、注射器、U型管和钩形管(长度大于1 000 mm的长直玻璃管用酒精喷灯加工而成)用乳胶管连接起来.

(2)将钩形管长直端悬挂于铁架台上,整个装置固定以便充气.

(3)将注射器活塞拉至尾部,将小气球口用细线多圈环绕然后活结固定在T形管一端,用滴管注水入长直钩形管直到水面与左边U型管顶部平齐;推进注射器活塞充气入小气球,直至气球直径接近量筒直径(若长直管内水压不够继续用滴管加入适当的水,若有气泡残留可通以长直细铁丝除之).钩形管左右两边水面高度差h0加上大气压(折算为水柱高度ha)即为球内气体压强(p0=ha+h0).h0不大,可通过注射器活塞或在长直管上加水控制大小,因而在一定范围内可定量获取任意气压,任意体积的气体.由于气球本身处在大气环境中,内外大气压平衡,h0实际上相当于气球弹性壁所施加的压强,因而该充气方式直接可给出气球弹性壁产生的压强.

(4)用另一根细线活结捆扎气球与T形管相接处(不是扎在T形管玻璃上,而是气球本身端口位置,与(3)捆扎处有一定距离),封闭气体,封闭瞬间对应的水柱差即为弹性膜所加压强.然后将(3)捆扎处细线解开,将气球从T形管上取下,并系上小钩码(其重量大于气球排开水的重量若干),则气球封闭的实际空气即为研究的近似理想气体,状态参数为(p0,V0,T0),压强p0和温度T0现场可测,体积V0可通过组合草木灰(或其它密度很少的粉末)用量筒直接测量[13],然后与用等温过程关系式p0V0=p1V1=C计算V0对比.

2.2.4 演示器简易制作

(1)取12号橡胶塞(上、下直径分别为56 mm、46 mm)打孔,取长200～300 mm细玻璃管(5 mm×7 mm×250 mm),用酒精喷灯对玻璃管两端截口进行平滑加工,然后将玻璃管套入橡胶塞.

(2)体积定标,将500 mL量筒套上橡胶塞(周边靠筒口一圈标上塞入量筒的位置),若量筒嘴处不能密封,可用长为30 mm左右的环形橡皮套(本实验取气球中段,剪掉端口和球顶)套上塞子与量筒连接处,外加橡皮筋固定加密,并检查气密性.然后取下塞子装水,待水面接近筒口塞入塞子时的位置,记下水的体积,塞上塞子于同样位置,改用注射器通过玻璃管往量筒内定量装水(内部不能有气泡),量管体积标记从大于量筒容积值(略高于橡胶塞上表面位置,可作为盛水初始体积)的某整数开始标记(如本文实验658 mL位置标记),采用纸带或标签纸做标记,用双面胶粘附于玻璃管上,刻度均匀,精度为0.1 mL(或直接测量液面至标记高度,然后通过每mm代表的体积进行换算,这样可避免设计体积尺度带).

2.2.5 使用方法

(1)用量筒测量钩码、气球膜(内填充水,排除空气)及所用细线的总体积V02以及气球橡皮膜的体积Vb.

(2)室温下(15.6 ℃)气球充气后[对应图1(a)h0=290.0 mm],从充气装置取下.用500 mL量筒测出能在量筒内完全淹没气球的草木灰的体积,然后将气球置于量筒内用上述给定的草木灰淹没,测出两者的混合体积,再减去草木灰、细线和气球膜的体积即为气球置于空气中时球内空气的体积V0=50.22 mL,气球状态0参数完全确定.

(3)组装气球、钩码与细线(要求钩码重量大于气球位于最高处时排开水的最大重量),将气球放入量筒,细线穿过玻璃管,加入室温(T0=t0+273.15 K)水直至水面靠近量筒口,套入橡胶塞至同样位置(要求玻璃管以下部分具有气密性).改用注射器加水至体积刻度初始位置(为便于读数可滴加1～2滴红墨水),气球处于量筒底部位置时,作为状态1[图2(b)],记录此时水和气球的总体积为

图2 室温15.6 ℃时气体等温变化实验

V1=v1+V01+V02

(1)

其中水的体积为V01(上述两次所加水量和),气球膜、钩码和细线的体积为V02,球内气体的体积为v1,玻璃管中水面至气球中心高度为h1(见文后附注证明).

(4)将气球拉至盛水量筒顶部,作为状态2[图2(c)],记录此时水和气球的总体积为

V2=v2+V01+V02

(2)

球内气体的体积为v2,玻璃管中水面至气球中心高度为h2.

(5)将量筒置于圆筒形水槽中,用稍高于室温的水(19.0 ℃)进行水浴加热,依上述步骤(3)和(4)同样方法获得状态3和4[参看图1(c),实物图略].将上述参数记入表1,计算并验证.

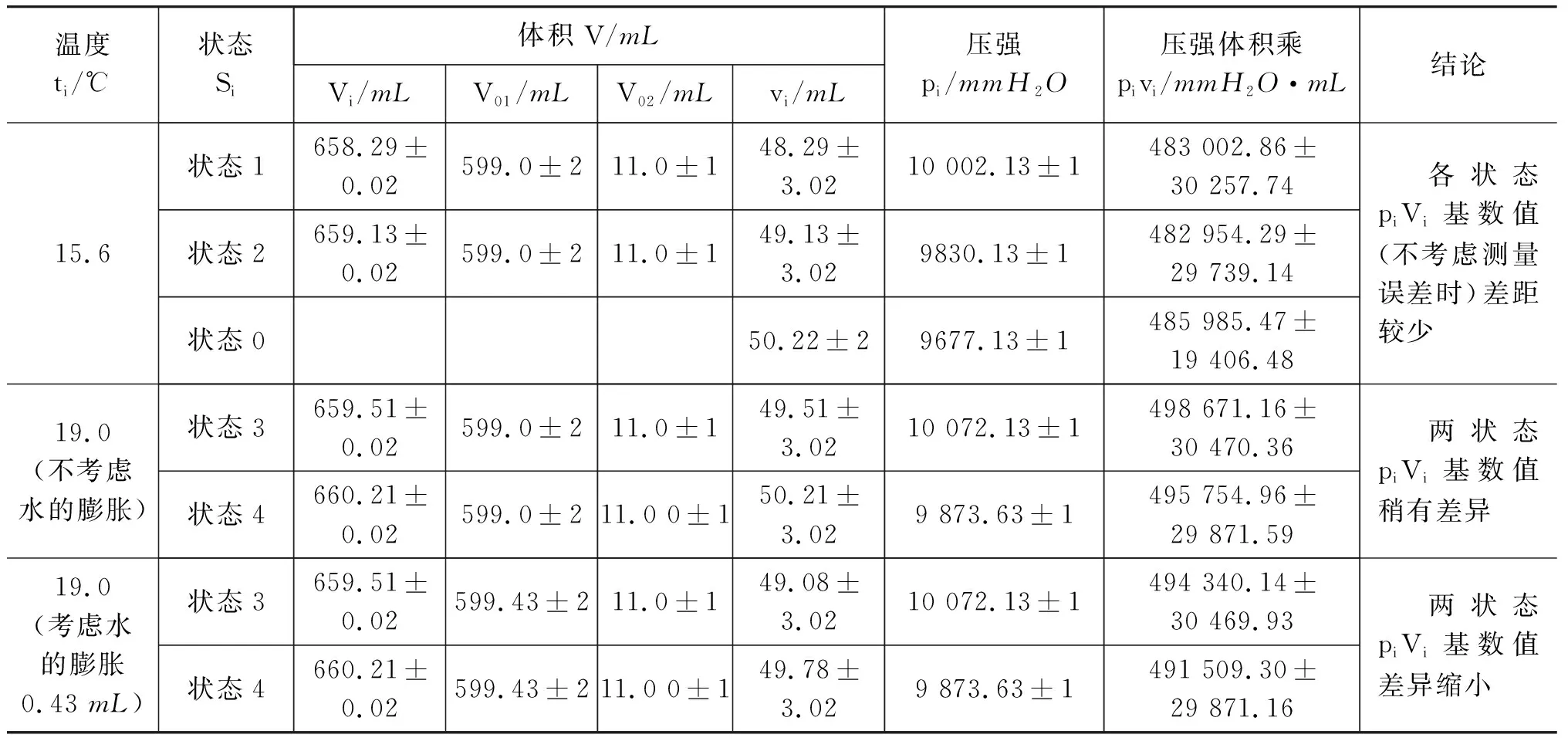
表1 气体等温变化

2.2.6 实验测试及数据分析

用简易充气测压装置填充气球,对应水柱高度为290 mm(h0),对应空气体积为V0,取该气球用于等温实验[见图2(a)].

(1) 等温过程分析

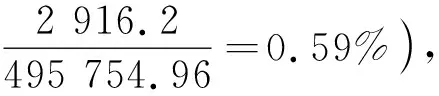
ΔV01=αV01Δt=2.1×10-4×599.0×
(19-15.6)=0.43 mL

(3)

此为考虑水膨胀时,气体体积的减少量(见表1).状态3、4对应的气压、体积乘积基数值差为

494 340.14-491 509.30=

2 830.84 mmH2O·mL

些许减少,说明测量误差占了大头,如气球在本实验中并非理想球体,状态变化时,气压中心的确定会带来测量误差.

对比室温下等温实验和升温后等温实验,升温后等温实验误差增大,鉴于上述分析,建议升高温度做等温实验时,所用水最好取自恒温箱较长时间保温的水,避免水温升高导致水缓慢膨胀.

(2) 气体状态方程验证

因为空气量给定,从状态1到状态3应该满足

(4)

对状态1

(5)

对状态3(不考虑水膨胀)

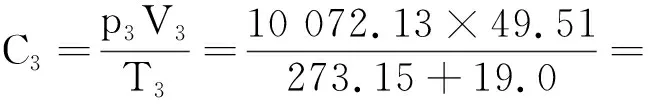
(6)

两者有33.96差距.

若考虑水膨胀

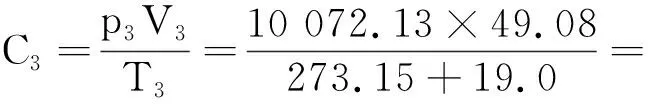
(7)

两者差距19.34,明显缩小,说明水的膨胀是应该要考虑的.

(3) 气球在空气中时其内气体体积的计算

取气球状态0和状态1,两者等温变化,符合

(8)

与2.2.5(2)测量结果V0=50.22 mL非常接近,说明实验设计是成功的.

3 教学应用

(1)应用于等压、等容变化及气体状态方程实验证实

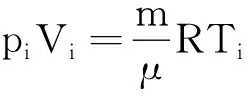
(2)应用于浮力分析,参考设计依据可用于分析浮力产生的根源.

(3)可用于测量空气的膨胀系数.在图1(b)基础上取气球状态1,状态参数为(p1,V1,T1).然后在图1(c)基础上,经水浴加热后取状态3(考虑水的膨胀),状态参数为(p3,V3,T3).然后参照膨胀系数的定义计算即可(具体从略).

4 设计说明

(1)作为玻璃制测量仪器,量筒不允许直接加热使用.但此处量筒仅作为普通容器使用,方便取材,并非利用其测量功能.且水浴加热控温50 ℃以下,量筒膨胀极为有限.

(2)量筒-橡胶塞-玻璃管组合的测试系统避免使用活塞类构件,不存在因漏气和摩擦带来的实验误差;同时也避免使用水银,不存在水银泄漏和挥发的危险.

(3)调整取气装置状态时要宜缓,特别是操作气球和注射器时,内部连通腔体不能受阻,否则,如腔体突然加压,会导致玻璃管中红墨水冲出.

(4)初次实验需要做好准备工作,消耗一定时间,装置做好后,操作是方便的.设计结构简单,取材方便,状态可控性强,现象直观,参数测定准确,误差小,实现用简单仪器、简易操作定量展示物理原理,低成本设计实验.可用于指导学生自制,进行研究性学习,适合于“控制变量法”本身的实验教学.

附录:证明水面下气球内气体所受水压等于水面至球心深度处产生的压强

证明1:定性分析(见附图1)

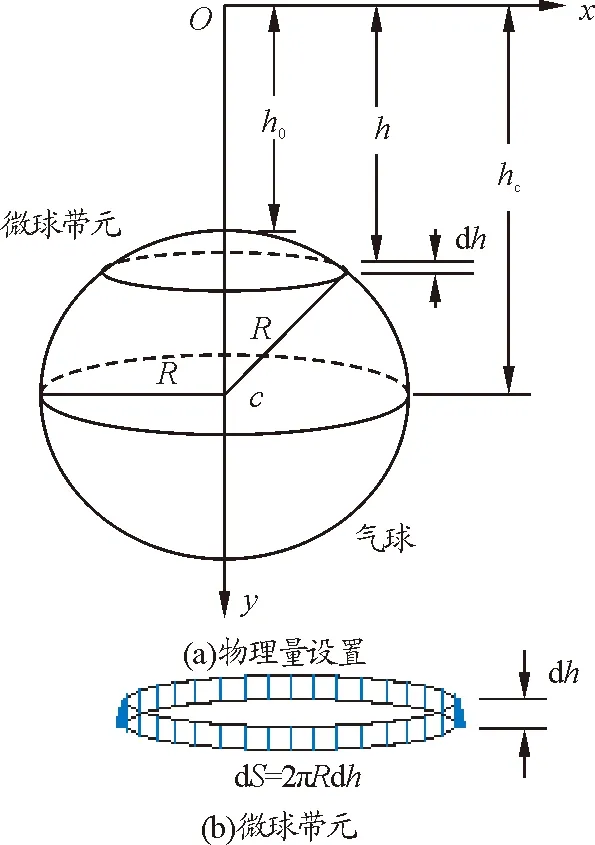
附图1 水面下气球内气体所受水压的计算,c为气球球心,半径为R

假定气球处于水面下h0深度处,球半径为R.球面上任意一点所受水的压强只跟深度有关,与球面形状无关,故球面上各点压强从ρgh0到ρg(h0+2R)不等,考虑到球形或近似球形的对称性,球面上所受压强平均值可表示为

证明2:定量计算

如附图1所示建立坐标系,在球面上取微球带,高度为dh,距离水面深度为h,微球带面积可表示为

dS=2πRdh

其上受力为

dF=ρghdS=ρgh×2πRdh

则球面上所受水的压力大小可表示为

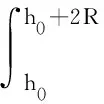
于是,气球表面所受平均压强可表示为

即为式(1).

以上分析考虑的仅仅是水对气球施加的压强,但不能认为气球内气压等于该气压,实际上由于气球膜本身弹力作用,球内气压要稍高于水压.