Spatial Modeling and Reliability Analyzing of Reconfigurable Intelligent Surfaces-Assisted Fog-RAN with Repulsion

Linlin Feng ,Zhizhong Zhang ,Haonan Hu ,Errong Pei ,Yun Li

1 School of Communication and Information Engineering,Chongqing University of Posts and Telecommunications,Chongqing 400065,China

2 School of Electronic and Information Engineering,Nanjing University of Information Science and Technology,Nanjing 210044,China

Abstract: Reconfigurable Intelligent Surface (RIS),fog computing,and Cell-Free (CF) network architecture are three promising technologies for application to the Ultra-Reliable Low Latency Communication(URLLC)scenario in 6G mobile communication systems.This paper considers a RIS-assisted Fog-Radio Access Network(Fog-RAN)architecture where a) the repulsively distributed Fog-Access Points (FAPs) communicate in a CF manner to suppress intercell interference,b) RISs are introduced into the CF network to avoid shadowing and enhance the system performance,and c) fog computing evolved as cloud services providers at the edge of the network and an enabler for constructing a multi-layer computing power RAN.Then,we derive and validate the integral form of the maximum F-AP offloading probability and Successful Delivery Probability (SDP) of this RIS-assisted Fog-RAN over composite Fisher-Snedecor F fading,where the spatial effects are reconsidered with the assumption that the F-APs are modelled as a Beta Ginibre Point Process (β-GPP).The numeric and simulation results indicate that for the investigated RIS-assisted Fog-RAN,the β-GPP-based deployment of F-APs can increase maximum of 8%of the SDP within the repulsion-effective range,compared with the Matern Cluster Process (MCP)-based ones.Also,deploying more RISs per F-AP offers more significant SDP improvements.

Keywords: β-GPP;Fog-RAN;reliability analysis;RIS

I.INTRODUCTION

The ever-increasing demand for mobile users’ broadband access has driven wireless networks far from the prototypal ones,where centralized network entities serve the users.As against this framework,the rising the sixth Generation (6G) networks are predicted to exploit programmable network infrastructures in a distributed,user-centric pattern.Compared to the fifth-Generation (5G) wireless communication system,the capacity and energy efficiency of 6G networks will be evidently strengthened [1].And the user-centricdriven focusing of the envisaged 6G networks on dispersedly located APs makes the exploitation on the spatial domain of the wireless environment more challenging.Moreover,a tendence of exponential traffic growth and Access Points (APs) densification is promoting even more subversive network redesigns to supply high-quality service to shielded users.As an architecture of centralized signal processing and cooperative resource management[2],Coordinated Multi-Point (CoMP) or Cloud-Radio Access Network (CRAN) is difficult to meet the demand for grew spatial bandwidth,namely the demand of 6G networks to transfer bits per second per cubic meter instead of simply bits per second [3].Meanwhile,C-RANs do not make the best use of computing and storage capabilities in Edge Nodes (ENs) [4].More importantly,on the occasion of poor conditions in the wireless environment,e.g.,existing communication infrastructure is insufficient to provide service to dramatically increased users or is disrupted partially by accidents,the CoMP approaches may fail to provide reliable services[5–7].RIS-assisted Fog-RAN of a CF version are actively researched as a promising technology framework that can tackle these challenges.

Fog-RAN was firstly proposed by Cisco to further make use of storage and computing capabilities in edge devices[8],thus addressing the challenging 6G’s Key Performance Indicator(KPI),such as URLLC and massive Machine Type Communications(mMTC).In comparison with C-RAN,Fog-RAN requires a relatively competitive computing and storage capacity.Thus,improving the storage and computing capacity of the F-APs at the network edges can facilitate the deployment of Fog-RAN.Fog-RAN provides a more applicable and efficient platform for local signal processing,computing,and caching,which relatively offloads the pressure on fronthaul compared to C-RAN[9].Evidently,Fog-RAN emerges as a primary candidate for realizing high spectral efficiency,reliable coverage/-transmission,and low latency design,which also provides a suitable underlying network framework for CF technology implementation to satisfy shielded users’Quality of Service(QoS)demand.

However,despite its ease and flexibility in integrating with other communication technologies,CF networks cannot achieve for invariable good QoS provisioning under harsh propagation circumstances,for example,in the existence of high attenuation due to large obstacles.To tackle this shadowing challenges issued from obstacles in CF Fog-RAN,a large quantity of F-APs or RISs are required to be deployed,of which the latter indubitably is the first option due to its flexible deployment,low power,and low cost.Recently,some studies have advocated exploiting CF massive Multiple-Input Multiple-Output (MIMO) with incorporated RISs to increase the communication capacity further [10],which highlight the advantages of Fog-RAN systems in computing and caching resources at the edge[11].Nonetheless,the accurate characterization of wireless fading channels can become a bottleneck in optimizing this RIS-assisted Fog-RAN while maintaining a continuously reliable transmission design.Thus,the application of the composite Fisher-SnedecorFfading models and Stochastic Geometry(SG) tools for efficiently solving complex networks’performance analysis problems has been steadily increasing in recent years.

The design of reliable Fog-RAN is highly dependent upon the accurate characterization of wireless fading channels mainly comprised of multipath fading and/or shadow fading.To better characterize them,a series of generalized and simplified fading models,especially shadowing ones,were investigated to fit to field measurements [12,13].The gamma-distributed and lognormally-distributed shadowing multiplied by another fading model originally arose as the multiplicative shadowing composite models,in which the consideration of channel propagation effects like the fluctuation of Line-of-Sight(LoS)components and the scattered waves are tackled unifiedly.However,these two applications for characterizing shadowing inherit the complicated formulation of a mixture of gamma or lognormal distributions,which considerably hinders their applicability for further analytical calculations.The contrast lies in the corresponding mathematical tractability for the LoS shadowing fading model where only the LoS components are affected by random fluctuation.Specially,despite providing a comparatively not so remarkable flexibility that not particularly useful for the effective characterization and modeling of some emerging wireless conditions,a Fisher-SnedocorFmodel with inverse Nakagami-distributed LoS shadowing constitutes a versatile framework for single shadowed models [14] and offers significant analytical advantages for system performance predictions,design issues,etc.This observed advantage becomes one key motivation for further modeling and analyzing the reliability of the investigated RIS-assisted Fog-RAN with SG tools.

Our consensus over the ENs deployment is that only with the ENs being placed following a specific rule is it usually possible to transfer a maximum amount of data successfully.Predictably,one of the most probable chances for enhanced transmission reliability and decreased delay lies in exploiting spatially distributed F-APs,relying on the control and use of interference from different F-APs.Thus,the ENs’irregular topology and RIS-assisted CF MIMO[15,16]are bound to make the reliability performance harder to model and analyze.Moreover,it is certified that SG is equalified to be an effectual mathematical tool in large-scale networks[17].Since modeling and analyzing the spatial topological relation of F-APs can contribute to the promotion of assimilating RIS-assisted CF MIMO,how to harness the interference from RIS-assisted F-APs based on SG is deserving of more exploration.

There have already been some existent studies[18–23] exploring the RIS-assisted Fog-RAN,CF Fog-RAN,and RIS-assisted CF MIMO,respectively.Presently,the concentrated studies on the elemental performance of these three kinds of systems,e.g.,[18–21],were mainly under the hypothesis of spatial irrelevancy of nodes’ distribution.Specially,a) for the RIS-assisted Fog-RAN:within[18],the power allocation decision minimizing the total energy consumption was determined for a hybrid RIS and massive MIMO relay assisted Fog-RAN through convex optimization method;b) for the CF Fog-RAN: in [19],the authors proposed an optimal method of offloading and resource allocation for CF Fog-RAN,based on the Deep Reinforcement Learning (DRL) approach,to reduce the overall delay;c) for the RIS-assisted CF MIMO:within [20],a architecture of RIS-aided CF massive MIMO systems was proposed,with the Wireless Energy Transfer (WET) technology integrated to RIS,and the optimal location of deploying multiple RISs was investigated with the designed transmission procedures and different hardware architectures of RISs.To maximize the Weighted Sum-Rate (WSR) of this WET-incorporated RIS-assisted CF MIMO,the authors of [21] adopted a Successive Convex Approximation(SCA)algorithm to tackle the jointly optimizing issues.Although the premise set in aforesaid studies may not coincide with most of the actual scenarios,these studies triggered the trial investigation into the performance of RIS-assisted CF MIMO with nonrandomly placed nodes[22,23].For instance,within[22],the impact of the RISs’spatial correlation on the uplink Spectral Efficiency (SE) for a RIS aided CF massive MIMO system over Rician fading channels was studied.Under the same circumstance with[22],the Generalized Maximum Ratio (GMR) combining was researched to maximize the uplink ergodic net throughput in[23].However,the modeling and analysis on the reliability performance of a RIS-assisted MIMO system incorporated with the effect of spatially correlated F-APs,the incorporation being conducted to exploit interference from different F-APs,is missing from the current works of literature.

Only a few works analyze the reliability of RISassisted CF systems by using SG tools despite of its being equalified to be an effectual mathematical tool for tractable analysis in a CF version of Radio Access Network (RAN) [24].Another fact must not be lost sight of is that the steered radio waves toward poor coverage locations also result in continuously growing accumulated interference increasing with the number of elements per RISs,thus reducing transmission reliability.Moreover,the ultra-dense and irregular deployments of F-APs make continuously cumulative interference pervasive and make the adverse effect of accumulated interference on reliable transmission more acute,especially for CF systems.The design criterion of higher reliability is of crucial importance and is consistent with the emphasized potential limitation on the reliability of CF systems in[25].Therefore,we firmly believe that a repulsive form among F-APs will inevitably appear in practical RIS-assisted Fog-RAN deployment for realizing reliable and sustainable networks.We summarize our motivations as follows:

· A great deal of the existent works is either limited to the analyses concerning the uplink SE and net throughput for the circumstance of independent and correlated fading channels in RIS-assisted CF MIMO systems or to the optimization algorithms applied to RIS-assisted Fog-RAN and CF Fog-RAN,while the reliability performance analysis is still a challenging task.Additionally,for reliability analysis,accurately characterized and tractable channel models,i.e.,the incorporated spatial and fading effects,are crucial to the investigated RISassisted Fog-RAN,while this is still in its infancy.

· This paper aims to evaluate the spatially repulsive effects on the reliable transmission of the RISassisted Fog-RAN by using SG tools.We introduce a general fading channel model,followed by applying SG tools to analyze this RIS-assisted Fog-RAN via aβ-GPP-based repulsive model.

· The Fisher-SnedecorFdistribution can well report the combined effects of multipath fading and shadowing[26]and has good analytical properties.Although some performance analysis under RISassisted case have been overall addressed only for gamma-distributed shadowing model and partially for lognormal-shadowing-based composite models,there is a lack of reliability analysis for large-scale repulsively distributed Fog-RAN under a more realistic and precise wireless propagation circumstance.Therefore,the reliability modeling and analysis of large-scale spatially correlated distributed RISassisted Fog-RAN incorporating the spatial distributions of F-APs and accurate characterizing of fading can complement these works.

As far as we know,we are the first to analyze the reliability performance in a CF version of RIS-assisted Fog-RAN under the SG framework.Compared with[22,23,27],the major dissimilarities can be generalized as below: 1) despite the fact that the correlation among the instantaneous received Signal-to-Noise Ratio(SNR)at a specific receiver may affect the eventual performance bounds,this correlations are introduced,but [20,21] did not meditate on the computation offloading strategy [28],neglecting the spatial correlation of massive task offloading;2) a novelFcomposite fading channel model is presented to model and characterize the composite fading channel with reflectors,exponential path-loss,fading,and shadowing for RIS-assisted Fog-RAN,while Rayleigh fading is assumed in [27];3) this SDP is analyzed numerically against the F-APs’density,the elements numbers per RIS,and the fraction of computation task.Hence,this work aims to tackle some of the challenging problems of analysis-based modeling in large systems shown by previous research work,fill in an omission in modeling and analyzing reliability performance of RIS-assisted Fog-RAN,and supply new analytical results for the RIS-assisted Fog-RAN performance in a SG framework.Our major contributions in this study can be generalized as follows:

· As far as our knowledge goes,this is the first analysis of a RIS-assisted Fog-RAN under composite fading and shadowing.We first express the F-AP Offloading Probability and SDP of the investigated RIS-assisted Fog-RAN using Meijer’s G function,and the simulations results of SDP are given to verify our theoretical findings and testify the potential benefits on reliability arising from the utilization of spatially repulsive F-APs by the RIS-assisted Fog-RAN.The results presented in this study can be used in the development of next-generation communication systems for applying RIS into Fog-RAN in a CF manner,thus providing a theoretical framework for investigating the reliability performance of this RIS-assisted Fog-ARN.

· We quantitatively compare the performance of conventional PPP-based andβ-GPP-based access network frameworks under accurately modeling practical channel with Fisher-SnedocorFdistribution,which proves that theβ-GPP-based RIS-assisted Fog-RAN framework is an effective approach for realizing the reliability increment in sophisticated wireless propagation environment.

We arrange the remainder of this paper as below.In section II,we outline the system model,consisting of the network model,RIS model,channel model,Local-Edge-Cloud Computing model,and the defined performance metrics (i.e.,F-AP Offloading Probability and SDP).In section III,we derive the analytical expressions of the F-AP Offloading Probability and SDP of the RIS-assisted Fog-RAN in terms of Meijer’s G function.In section IV,we provide some numerical results of these metrics and the Monte Carlo simulation results of SDP to corroborate our theoretical derivations.Finally,we conclude this paper in section V.

II.SYSTEM MODEL

2.1 Network Model

We consider a general RIS-assisted CF Fog-RAN concluding a lot of repulsively distributed F-APs with unified computing resources and capabilities,connected to a cloud computing center via optical-fiber fronthaul links,as shown in Figure 1.The irregular polygons surround by the green dotted line are the GPP Voronoi Tessellation(GVT).To fully exploit the computing resources at the network edge,we propose to deploy RISs in this Fog-RAN to enhance the computation offloading links for the UEs at the edge of coverage areas or those behind LoS blockages[29].This enhancement is especially beneficial for the delay-sensitive applications by assisting the transmission,hence reducing or even eliminating the end-to-end delay.

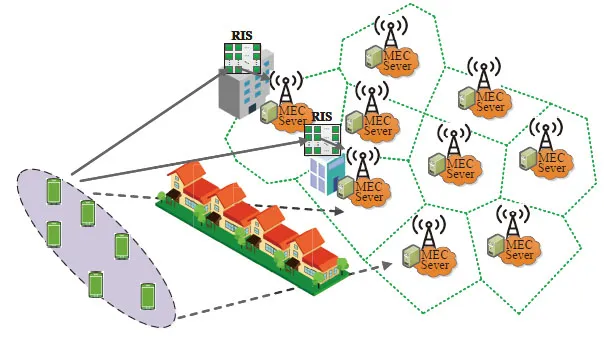
Figure 1.An illustration of RIS-assisted Fog-RAN.

The locations of F-APs,denoted by{Xj},j∈Nb,whereNbis the number of F-APs,are modelled by aβ-GPP with densityλb.And a group of active User Equipments (UEs) are scattered in a circle region of radiusaround the F-AP following uniform distribution with densityλm[27].That set of UEs are denoted byYi,j,i∈Nj,whereNjis the number of UEs in the covered region of the F-APj.In our works,{Xj}is defaulted to be the Master F-AP ofYi,jto guarantee each UE has a“Master AP”to be anchored to.

The distributed large RIS boards,each comprised ofNpassive reflecting elements,are deployed in the vicinity of the F-APs,ensuring them reflect the maximum power toward F-APs [30].It is noted that the relatively small transmit distances between F-APs and the nearly co-located RISs boards can be ignored.And the RISs boards’horizontal height usually exceeds that of their F-APs.

2.2 RIS Model

For not loss of analytical tractability by the spatial repulsion introduced,the RIS’s reflecting model ofRlis represented by

To not impose restrictions on the duplex mode,a fully passive approach is adopted to acquire the Channel State Information (CSI).Taking the uplink as an example,first,the direct and cascaded UE-RIS-AP channels are estimated at the F-APs based on the orthogonal pilots sent by the UEs;Second,based on the estimated CSI,the joint design and optimization of RIS reflection coefficients and beamforming vectors are executed at the F-APs and then sent to the RIS controller;Third,the RIS controller sets or updates the reflecting coefficients accordingly.More specifically,once the Statistical CSI(S-CSI)is estimated and fed back to the F-APs,the RIS long-timescale phase beamforming design is performed at the F-APs and then is fixed.In the meanwhile,the short-timescale transmit beamforming vectors at the F-APs are dynamically designed based on Instantaneous CSI (ICSI).This two-timescale beamforming will reduce the complexity of CSI estimation to a certain extent.

2.3 Channel Model

Each link from a UE to an F-AP is presumed to experience path loss and Fisher-SnedecorFcomposite fading and shadowing.The pathloss is denoted byl(r)=r－α,whereris the distance andαdenotes the pathloss exponent.The transmit power of UEs adhibits a fractional channel inversion rule given asPi,j=pl(Ri,j)－ϵ[31],wherepis the maximum transmit power,Ri,jis the distance between the F-APjand its covered UEiwithRi,j=|Yi,j-Xj|,andϵis the power control factor.

The power gainhd,n,n∈{1,2,...,N}from a UE and its F-APs(i.e.,Master or cooperative F-APs)with distancedis modelled as independently distributed Fisher-SnedecorFRandom Variables(RVs)with the following Probability Density Function(PDF)[32]

wheremnandmsnseparately characterize the indexes of the fading severity and shadowing seriousness of then-th RV,=E[hn]represents the average power,B(·,·)denotes the Beta function[33,Eq.(8.384.1)].

Without loss of generality,the test F-APX0can be placed at the origin,from which the cooperative F-APsXjcan be regarded as a reduced Palm version of theβ-GPP.Correspondingly,a test UE ofX0is located atY0,the link distance from the interfering UEYi,jand its Master F-APXjis denoted byRj,and the composite fading and shadowing is expressed byh|Rj|,being simplified ashj.The covered UEsYi,jofXjare allocated with orthogonal frequency resources.Consequently,the Signal-to-Interference Ratio (SIR) ofX0can be expressed as follows:

where Φkandhkdenote the set of interfering UEs and the power gain over thek-th sub-channel,respectively.

2.4 Local-Edge-Cloud Computing Model

1)Localcomputing.For local computing without no communication to F-AP,the final delay of task processing is equal to the local computation delay.Further,the computation capability of UEi,denoted byfi,represents the CPU cycles required to process a unit bit of data,and thus the computation delay of computing a task with a data sizeand a processing densityγican be expressed as.Referring to the real measurements in practice[34],the processing density and data size of data business applications,for example,video transcoding,are about 1000 cycle/bit and 1000 KB,respectively.

2)F-APOffloadingprobability.For F-AP computing,the tasks are uploaded to F-APs for processing,and thus both communication delay and computation delay are involved.Given that the F-AP servers are customarily co-located with their F-APs,the final delay of task processing can be calculated bywherefjis the computation capability of F-APjandis the average data rate.Additionally,T0is the expected computation time of a task in the case of a single server.

3)CloudOffloadingprobability.The occurrence of blockage,the arrival of tasks,and the servers’processing are all independent of each other.Then,the probability of the first blocking occurring and the number of blocking occurrences are only related to the length of time.

2.5 Investigated Performance Metrics

In this study,we pay attention to the maximum FAP offloading probability and SDP,i.e.,the reliability function.First,the maximum F-AP offloading probability,which is obtained by calculating the following probability that UEi,its Master F-AP being chosen as F-APj,having a higher uplink transmission rate than a thresholdθ,i.e.,

whereTjis represented by a Bernoulli distribution,i.e.,Tj～Bernoulli(β),Bis the sub-channel bandwidth,andθis the preset rate constraint of guarantee network capacity.

The reliability function,i.e.,SDP,can be obtained by calculating the following probability that the required delay for completing the computation processing being smaller than a target thresholdt0[36]

III.PERFORMANCE ANALYSIS

3.1 F-AP Offloading Probability Analysis

As can be observed,the power gain ofk-th subchannel for the test UE,is a sum of independent Fisher-SnedecorFRVs.Using the definition in (1),a property of hypergeometric functions[33,Eq.(9.34.7)] and the algebraic transformation[37,Eq.(1.4.2)],the PDF ofhkis thereby given by

Proof.See Appendix A.

In this work,we do not consider the user privacy issue,that is,are only relevant to the attributes of the computation task(i.e.,processing densityγi)and the computation capability of a UE and its allocated F-APs,the impact of which on the transmission reliability can be analyzed with given parameter values.Thus,the expression of this first probability is expressed in Theorem 1 as below.

Theorem 1.FortheinvestigatedRIS-assistedFog-RAN,theprobabilityoftheuplinktransmission ratebeinggreaterthanathresholdθcanbecalculated by

This probability is influenced by the sub-channel bandwidthB,the rate thresholdθ,the F-AP densityλb,and the computation capabilityfiof UE.

Theorem 2.FortheinvestigatedRIS-assistedFog-RAN,astheF-APpositionstendingtobeaPPPwithoutrepulsion,theprobabilityisobtainedasfollows:

Proof.See Appendix C.

3.2 Successful Delivery Probability Analysis

In conformity to the mathematical definition of SDP shown in (3),we can obtain the corresponding theoretical expression of the SDP in Theorem 2 as below.

Theorem 3.TheSDPoftheinvestigatedRIS-assisted Fog-RANwiththeLocal-Edge-CloudcomputationoffloadingmodelisgivenbyProof.See Appendix D.

Possessed with the above result,the SDP for a particular UE in the investigated RIS-assisted Fog-RAN can be obtained.Accordingly,we calculate the SDP numerically in Section IV.

Theorem 4.TheSDPoftheinvestigatedRIS-assisted Fog-RANwiththeLocal-Edge-CloudcomputationoffloadingmodelandPPP-distributedF-APsisgivenby

Proof.See Appendix E.

Comparatively,whenβdecreases gradually and converges to 0,the positions of a specific F-AP’s and its covered UEs trend toward a MCP,i.e.,the F-APs’positions tending to be a PPP without repulsion.The comparative MCP-based results of reliability for the investigated RIS-assisted Fog-RAN are provided in Section IV.

IV.SIMULATION RESULTS

In this section,we first numerically analyze the F-AP Offloading Probability against the F-AP densities,the mobile densities and processing density.Additionally,the verification results of the SDP of the RIS-assisted Fog-RAN under spatially correlative ENs deployment strategy are presented.Furthermore,the average rate and optimal values ofθversus the mobile densities are also plotted.In the verification,the values of main parameters are itemized in Table 1.

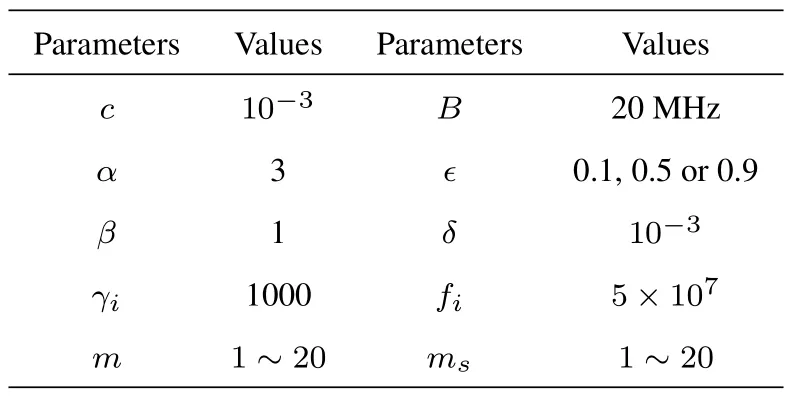
Table 1.The main parameters for simulation.

4.1 Maximum F-AP Offloading Probability

In Figure 2,we present the maximum F-AP offloading probability and mobile density trade-off curves with different values of F-AP density and UEs’ computation capability.First,we observe that the tripleincreased computation capability of UEs significantly raises the maximum F-AP offloading probability especially when the mobile densityλmis low.In addition,theβ-GPP-based model outperforms the MCP-based ones on the guiding ability of sinking the core business to the network edge,thus enhancing the various types of service quality.This suggests that the computation capabilities of UEs constitute a dominating influence onρi,jof the considered RIS-assisted Fog-RAN.Second,with an increase in the mobile density,the impact ofλbon the maximumρi,jperformance becomes more notable for small values offi.Moreover,within a relatively small variation for the large values ofλm,ρi,japproaches a fixed value determined by ENs’ maximum workload processing capacity,indicating that the joint channel gain tends to be constant.In other words,the critical application of RISenabled cooperative intelligent wireless environments firstly lies in the autonomous reconfiguration to overcome the detrimental effects,however,the effectiveness of that RIS-enabled systems can be further challenged by the load capacity dictated by the computing power of edge nodes.To conquer this constraint of incorporating RIS into Fog-RAN,it is therefore crucial to be equipped with sufficient computation resources for accommodating the task from edge.

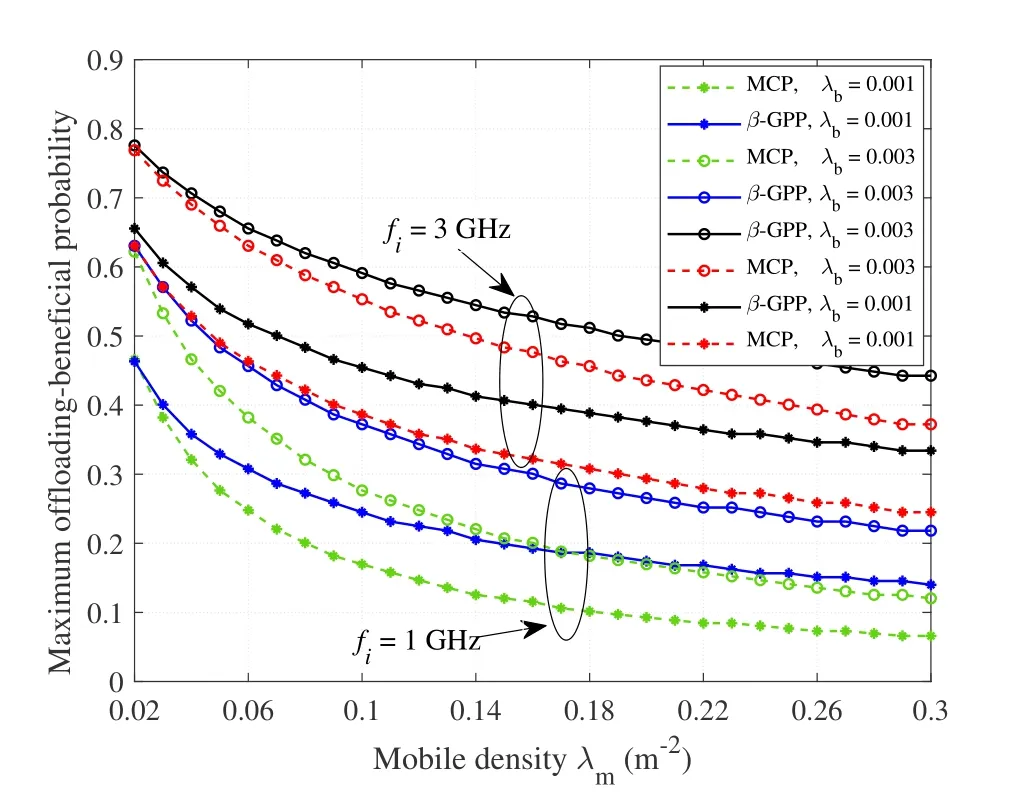
Figure 2.Maximum F-AP Offloading Probability vs.λm with different values of λb and fi.

In Figure 3,the results show that the average transmission rate increases with the decreasing ofϵand the boost in transmission rate across the same 2-fold increase of F-APs’density is more noticeable with lower power control index atϵ=0.1.From another perspective,a smaller power control factor index results in a higher SIR,which raises the probability of task being uploaded to F-APs.Additionally,the impact ofλbon the average transmission rate becomes more significant for large values ofλm.This is due to that more quantity of cooperative F-APs can induce increasing aggregate interference,which decreases the average data rate.

Figure 3.The average rate vs. λm with ϵ being 0.1,0.5 and 0.9.

Figure 4 confirms that a far higher proportion of cooperative RISs is more helpful to improve the average transmission rate.From the average rate standpoint,on the other hand,the curves with theλb=0.003 setup is always close to that corresponding toλb=0.001 withNbeing 8 or 16.This highlights the need of using powerful computing capabilities at the ENs to take better advantage of the RISs.An observation on doubling the number of cooperative RISs from 8 to 16 corresponds to about 100M bit/s increase in average transmission rate.This increasing marginal benefit is instructive in engendering the next generation of RISempowered wireless networks.Thus,from a design perspective,this may be insightful for the practical implementations of RISs.

Figure 4.The average rate vs. λm with ϵ being 0.5.

4.2 Successful Delivery Probability

In Figure 5,there is a small gap between the theoretical and approximated SDP,which verifies the correctness of our derived SDP.It is also shown that the variance on the uplink power control index makes very little difference to the SDP.Following this clue,which reveals that under the given propagation scenario,i.e.,simultaneous multipath fading and shadowing,and under stringent control of UE transmit power,the SDP of the investigated Fog-RAN remains relatively unaffected as the target delay increases,the interference from parallel mass signals can be controlled to the extent in relative-stable quality for communication.

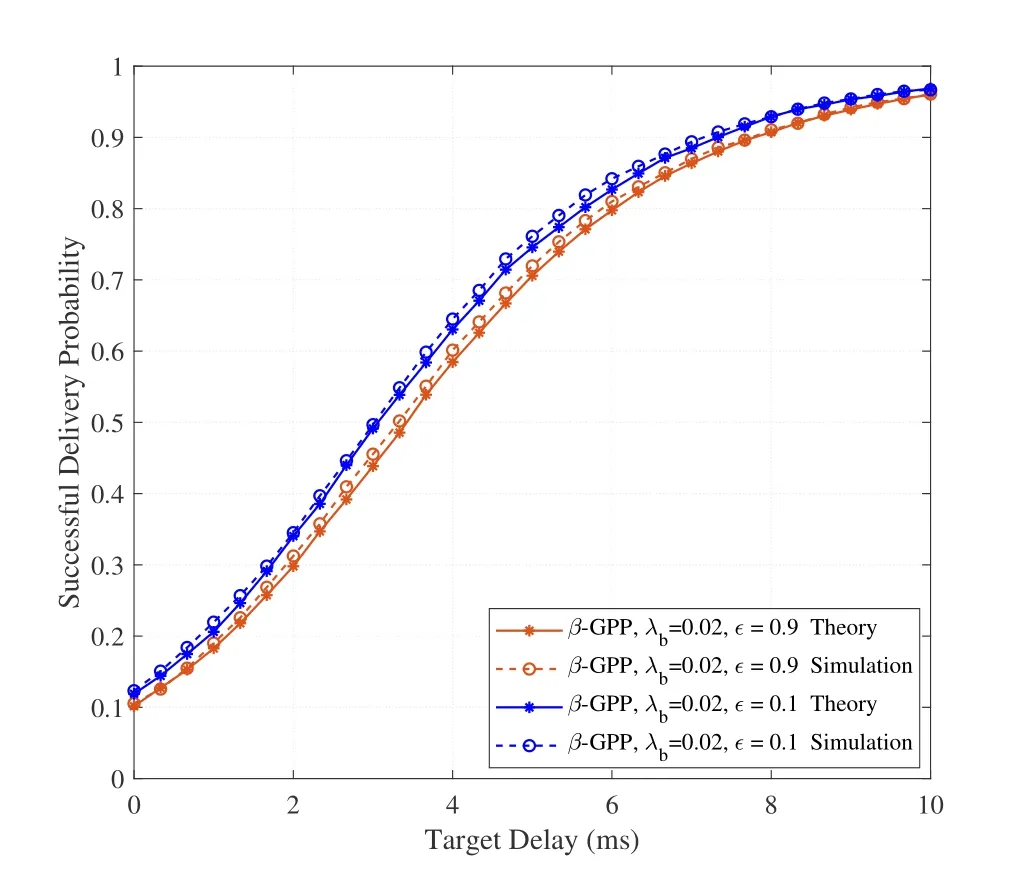
Figure 5.The SDP vs. the target delay with ϵ being 0.1 and 0.9.

In Figure 6,theβ-GPP-based and MCP-based SDP curves under four cases ofT0being 0.01sintersect at points (xi,yi),i=1,2,3,4,respectively,and[0.1,xi],i=1,2,3,4 represent the repulsion-effective range,where theβ-GPP-based aggregate interference can increase a maximum of 8%of the SDP.The set of inequationsy1＜y2＜y3＜y4indicate that the effectiveness of the LoS components provided by RISs as the assistant channel on enhancing the signal transmission cannot be ignored.Moreover,it is observed that |y2-y1|＜|y3-y2|.These inequalities indicate that the double-increased quantity of F-APs outperforms the fourfold-increased amount of elements per RIS in terms of SDP due to that the added F-APs can also provide computing resources,not just additional transmission paths.Furthermore,the impact of repulsion between the cooperative F-APs on SDP performance becomes less significant for large value of fraction of computation task.This mainly is because the allocated computing resources and capabilities to F-APs come to be inadequate when the quantity of computation tasks rises.Last but not least,we can see that the solid curves is always lower than the dashed curves in the case thatx＞xi,which seems to contradict our statement above.This contrary behavior is the indirect result of the interfering UEs being scattered in the vicinity of the Master F-APs.The occurrence of crosspoints can be delayed or avoided by keeping the GPP relatively low intensity.

Figure 6.Successful Delivery Probability vs. fraction of computation task,where T0=0.01s.

In Figure 7,we compare the optimal threshold of the original tasks being strategically uploaded to FAPs in the investigated RIS-assisted Fog-RAN with different values of F-APs density.The results display that the optimal values ofθincreases with the growth of the processing densityfiof task.The main reason is that the maximum value ofdecreases whenfiincreases,and thus remaining more computing tasks to be processed at the UEs can reduce the average delay.Further,the optimal values ofθrequired for the case ofλbbeing 0.001 is usually larger than that under the case ofλbbeing 0.002 and 0.003.The inducement behind is immediate and intelligible.The decrease in quantity of alternative F-APs available to be selected as cooperative nodes makes incessantly generated tasks more difficult to be offloaded to F-APs.

Figure 7.The optimal values of θ vs. λm with different values of λb and fi.

V.CONCLUSION

RISs are an innovative paradigm under the background of wireless communications,and the predictable benefits stemming from the employment of RISs had been demonstrated in the academic research.In this article,we look at enabling the potential technical approaches toward more reliable Fog-computing,relying on an architecture of RIS-assisted Fog-RAN based onβ-GPP,and aim to alleviate the disruptive effects of RIS links with the introduced spatial repulsion.Moreover,the trivial effect of the power control factor on the SDP implies the solid anti-interference ability of this network.Further,Local-Edge-Cloud computing power plays a dominant role in achieving ultra-high reliability for 6G networks.In future,more sophisticated channel model remains an under-explored research challenge.We also are hopeful that the theoretical insights given in our work may be useful for the future adoption of Machine Learning(ML)at the edge of RAN with this background of emerging RISs.

The following research will be considered in future work: 1)The effects of F-APs’spatial effects on the physical layer security across a large-scale RISassisted Fog-RAN cooperating in a CF manner;2)The optimal caching strategy of the investigated RISassisted Fog-RAN under a constraint on the maximum SDP;3) Minimize the total delay by jointly optimization for obtaining the optimal edge computing resource schemes under the constraint of meeting energy-efficiency demands.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China under Grants 62001238,62071077,and 61901075,in part by the Special Project for Industry of Ministry of Industry and Information Technology of China under Grant TC210H02P/2.

APPENDIX

A Proof of Lemma 1

B Proof of Theorem 1

where2F1(α,β,γ,z) is the Gauss hypergeometric function [33,Eq.(9.111)].The CDF ofgcan be expressed as follows:

The generation of aβ-GPP can be created by retaining eachQjwith probabilityβindependently,andQj～Γ(j,β/c).As a result,the PDF ofQjis given as:

According to (2),this probabilitycan be transformed as follows:

Moreover,by assignment ofh0l(|Y0|)1－ϵ=a0and=g0,the result can be translated into the following form as:

Furthermore,we can calculate the expectation result in(B.5)as:

C Proof of Theorem 2

With the F-AP positions being a PPP without repulsion and by following the procedure of the calculations,such as (B.2) and (B.4),the probabilityis firstly derived as follows:

Similar to(B.6),the expectation result in(C.1)is obtained as follows:

By incorporating (C.2) into (C.1),the result in Theorem 2 can be eventually yielded.

D Proof of Theorem 3

Given the definition in (3),the SDP expression of the investigated RIS-assisted Fog-RAN can be transformed as below:

By incorporating the result in (B.3) into (D.1),and some mathematical transformations,the result in Theorem 3 can be easily obtained.

E Proof of Theorem 4

Based on (C.2),we can formulate (D.1) in the same way.Upon changing to the assumption of homogeneous PPP with densityc/πand applying the characteristic function evaluation [38,Theorem 2.6],we arrive at(9).The proof is completed.